blueqatで量子ゲートを操作し、量子もつれ（エンタングルメント）状態を生成する #量子コンピュータ

この記事の目的

量子もつれ(エンタングルメント)ついてに説明し、blueqatを使用した量子回路による量子ゲート計算で量子もつれ状態を生成し、その量子状態を確認します。

blueqat … 量子コンピュータ・シミュレーターです。株式会社blueqat(東京・本郷)が開発及びリリースを行っています。詳細は、下部の関連情報欄をご参照下さい。

量子もつれ(エンタングルメント)とは

量子もつれ(エンタングルメント)は、物理学の研究分野の一つである量子力学で研究されている素粒子の相互作用に関する研究の一つで、天才物理学者アルバート・アインシュタインが「不気味な遠隔作用」と呼んだ、物理現象の一つです。

量子もつれ(エンタングルメント)は以下のように言うことができます。

2つの量子が量子もつれの状態(エンタングルメント)にあるとき、どれだけ距離が離れていてもその2つの量子の一方に測定が起きると、直ちにもう一方の量子の状態が影響され、位置や運動量を変えてしまう。

上記の事象はまるで魔法のようですが、厳密な実験で確認されています。

量子コンピューターでは、この事象を応用し、様々な量子計算に使用することができます。
特に、絶対に破ることのできない暗号技術である量子暗号の基礎的原理として注目されています。

量子ゲートでのテンソル積と量子もつれの定義

まず、テンソル積について説明します。ここでは、分かりやすいように2次元で説明します。
テンソル積とは、記号「$\otimes$」で表されるベクトル同士の計算で、以下のように定義されます。

2次元のベクトル(ケットベクトル) $\psi$ (プサイ)と $\phi$ (ファイ)を以下のように定義します。

|\psi〉= \binom{a_0}{a_1}\\
|\phi〉= \binom{b_0}{b_1}

このとき、テンソル積は以下のようになります。
(記号「:=」は定義するという意味です)

|\psi〉\otimes|\phi〉:= \binom{a_0|\phi〉}{a_1|\phi〉} := 
\begin{pmatrix} a_0b_0\\a_0b_1\\a_1b_0\\a_1b_1\end{pmatrix}　...　(1)

量子ゲートによる理論的な量子もつれの定義は以下のように表現されます。

量子もつれ状態とは、2量子ビット系の状態において(1)の状態を書き表すことができない状態のことである

一般に、n次元ベクトルは、n個の正規直交基底ベクトルで表すことができます。
ここで、正規直交基底とは互いに直交する単位ベクトルです。
2次元ベクトルの場合、以下の2個の正規直交基底でベクトルを表現することができます。

x_1\begin{pmatrix} 1\\0 \end{pmatrix} + x_2\begin{pmatrix} 0\\1 \end{pmatrix}

上記の2次元正規直交基底で表現できるベクトルのテンソル積は、以下の(2)と(3)の2種類なので、

\begin{pmatrix} 1\\0 \end{pmatrix}\otimes\begin{pmatrix} 0\\1 \end{pmatrix} =
\begin{pmatrix} 0\\0\\1\\0 \end{pmatrix}　...　(2)\\
\begin{pmatrix} 0\\1 \end{pmatrix}\otimes\begin{pmatrix} 1\\0 \end{pmatrix} =
\begin{pmatrix} 0\\1\\0\\0 \end{pmatrix}　...　(3)

次のようなベクトルは、2次元の正規直交基底で表現することができないことがわかります。

\begin{pmatrix} 1\\0\\0\\1 \end{pmatrix}　...　(4)

上記のベクトル(4)は、量子もつれ状態(エンタングルメント)の一つです。

blueqatで量子もつれ状態を生成する

では、上記で確認した量子もつれ状態を量子コンピューター・シミュレーターのblueqatで生成してみましょう。
今回は、量子回路図を以下としました。(量子回路図1とします)

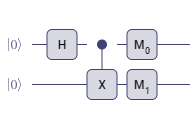
まず、上記量子回路図1について、机上で量子計算を行い、状態の振る舞いを確認します。

①入力は2量子ビットでそれぞれ|0〉ベクトルで初期化されていますので、この状態は以下のように表すことができます。

|00〉

②1量子ビット目にH(アダマール)ゲートを適用します。2量子ビット目は何も適用しないので、恒等演算Iとします。

|00〉　\longmapsto　(H \otimes I)|00〉

③上式は、テンソル積計算の公式から以下のように展開することができます。

\begin{align}
(H \otimes I)|00〉 &= (H \otimes I)|0〉 \otimes |0〉 \\
&= (H|0〉) \otimes (I|0〉)
\end{align}

④H|0〉,I|0〉はそれぞれ以下のようになるため

H|0〉 = \frac{1}{\sqrt{2}} (|0〉 + |1〉) \\
I|0〉 = |0〉

⑤上記を用いて、

\begin{align}
(H \otimes I)|00〉 &= \frac{1}{\sqrt{2}} (|0〉 + |1〉) \otimes |0〉 \\
&= \frac{1}{\sqrt{2}} (|00〉 + |10〉)
\end{align}

⑥次に、1量子ビット目と2量子ビット目に制御NOT演算子(CNOT:シーノット)を適用します。

CNOTを適用　\longmapsto　CNOT\bigg(\frac{1}{\sqrt{2}} (|00〉 + |10〉)\bigg)

⑦上記を展開して以下を得ます。

\begin{align}
CNOT\bigg(\frac{1}{\sqrt{2}} (|00〉 + |10〉)\bigg) &= \frac{1}{\sqrt{2}} (CNOT(|00〉) + CNOT(|10〉)) \\
&= \frac{1}{\sqrt{2}} (|00〉 + |11〉)
\end{align}

よって、量子回路図1により得られる量子状態は以下のようにケットベクトル|00〉と|11〉の合成となり、それぞれの確率振幅が$\frac{1}{\sqrt{2}}$であることから、確率は0.5ずつとなります。

\frac{1}{\sqrt{2}}|00〉 + \frac{1}{\sqrt{2}}|11〉

次にプログラムで量子計算を実行します。
blueqatでのプログラムコードは以下のようになります。

entanglement.py

from blueqat import Circuit

# 2量子ビットの回路を生成
c = Circuit(2)

# 1つ目量子ビットにHゲートを適用
c = Circuit().h[0]

# 1つ目及び2つ目量子ビットに制御NOT(CNOT)ゲートを適用
c.cx[0,1].m[:]

# 実行回数を1000回に指定して量子計算を実行
c.run(shots=1000)

実行結果は以下でした。

Counter({'00': 502, '11': 498})

blueqatによる計算結果は、|00〉と|11〉がそれぞれ502回、498回の出現で、比率はだいたい1:1と近似します。つまり、確率がそれぞれ0.5(50%)ずつとなりました。
上記の結果は、机上の計算結果と一致することから、量子もつれ状態が生成されていることがわかります。

以上より、量子回路図1とblueqatによる量子ゲート計算で量子もつれ状態を生成することができました。

ご意見など

ご意見、間違い訂正などございましたらお寄せ下さい。