More than 3 years have passed since last update.

Blueqatで簡単な頂点被覆問題を解く

Posted at 2020-05-23

この記事の目的

組合せ最適化問題の代表的な問題の一つである頂点被覆問題(Vertex Cover)を、量子アニーリングで解く方法を確認します。量子アニーリングにはMDR社のオープンソースフレームワークであるBlueqatを使用します。

頂点被覆問題について

頂点被覆問題(Vertex Cover)とは、グラフ・ネットワーク問題の一つで、複数の頂点とそれを結ぶ辺があり、どの辺も少なくともその始点または終点のどちらかが、二つにクラス分けした頂点群のうちの一方のクラスに属する頂点(のいずれか)と接するもので、そのクラスを最小にする問題です。

数学的に説明すると以下となります。

頂点の部分集合 X \subseteq V に対して、どの枝も少なくとも一方の端点が\\
Xに含まれるとき、すなわち、任意の (i,j) \in E に対してX \cap {i,j} \neq 0 が\\
成り立つとき、Xを頂点被覆という。

以下に図を示します。
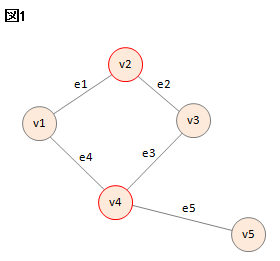
ここで、v1,v2,v3,v4,v5は頂点を、e1,e2,e3,e4,e5は辺を表します。
図1の通り、どの辺についてもその端点の一方が赤丸の頂点に属しています。
赤丸の数が最小になるケースを求める問題が頂点被覆問題です。

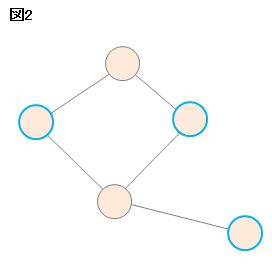
例えば、下の図2のような頂点を選択した場合、頂点の数は3個なので最適解にはなりません。

頂点被覆問題を量子アニーリングで求める

今回使用するオープンフレームワークのBlueqatや検証環境については、以下をご参照下さい。

■Blueqatでナップサック問題を解く一例
https://qiita.com/ttlabo/items/537564c90056a6d56879

この問題を量子アニーリングで解く際には、イジング模型に基づく定式化を行います。
頂点被覆問題(Vertex Cover)に関する定式化は、Andrew Lucas氏による論文を参考にすると以下となります。

\begin{eqnarray}
ハミルトニアン\;H\;&=&\;H_A\;+\;H_B\\
H_A\;&=&\;A\sum_{u,v}^{}(1 - x_u)(1-x_v)\\
H_B\;&=&\;B\sum_{v}^{}x_v\\
但し、B<Aとする。
\end{eqnarray}

ここで、u,vの取り方を以下のようにします。
u,vがそれぞれ独立して頂点v1～v5を取るわけではありません。
u,vは図1に従い、取り得る頂点の組み合わせが限定されるため、以下の組み合わせとします。

(u,v)の組み合わせ=(1,2),(1,4),(2,3),(3,4),(4,5)

今回はAの値を1、Bの値を0.5としました。
ハミルトニアンを式展開すると以下となります。

H=5-\frac{3}{2}x_1-\frac{3}{2}x_2-\frac{3}{2}x_3-\frac{5}{2}x_4-\frac{1}{2}x_5\\
+x_1x_2+x_1x_4+x_2x_3+x_3x_4+x_4x_5

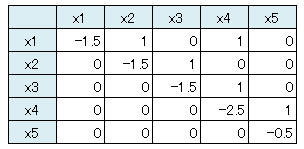
従って、QUBOマトリックスは以下となります。

Blueqatのプログラミングとその解

以下、Blueqatのプログラムを掲載します。

vertex_cover.py

import blueqat.opt as wq

a = wq.opt()
a.qubo = [
    [-1.5,    1,    0,    1,    0],
    [   0, -1.5,    1,    0,    0],
    [   0,    0, -1.5,    1,    0],
    [   0,    0,    0, -2.5,    1],
    [   0,    0,    0,    0, -0.5]]
    
result = a.sa(shots=500,sampler="fast")
z = wq.counter(result)

print(z)

プログラミングは以上です。
今回の計算結果、以下の解が得られました。

Counter({'01010':439, '10101':33, '10110': 28})

上記の解を見ると、一番目の解が最適解とわかります。
x1～x5は以下の値を取ります。

x1	x2	x3	x4	x5
0	1	0	1	0

ここでは、0,1はクラス分けを意味しています。
0を取る頂点のクラスと、1を取る頂点のクラスに分かれます。

このクラス分けが今回の問題の解答となります。
x2,x4が図1の赤丸の頂点、x1,x3,x5がその他の頂点を意味します。

以上で頂点被覆問題の解が得られました。

出典

■参考論文
　Ising formulations of many NP problems
　https://www.frontiersin.org/articles/10.3389/fphy.2014.00005/full

ご意見など

ご意見、間違い訂正などございましたらお寄せ下さい。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up