この記事の目的
この記事の目的
量子コンピュータのアルゴリズムの一つであるQAOA(Quantum Approximate Optimization Algorithm)について、その基本及びblueqatを使用したプログラミングの解説を行います。
 QAOAの仕組み【理論編】
QAOAの仕組み【理論編】
ここではQAOAの理論を解説します。
直接、プログラミングの実装に入りたい方は【実践編】へ進んで下さい。
QAOA(Quantum Approximate Optimization Algorithm)は、量子近似最適化アルゴリズムと呼ばれ、量子ゲート方式による組合せ最適化問題の解を求めるためのアルゴリズムです。
QAOAについては、以下の論文で提唱されています。
![]() A Quantum Approximate Optimization Algorithm
A Quantum Approximate Optimization Algorithm
(by Edward Farhi, Jeffrey Goldstone, Sam Gutmann)
https://arxiv.org/abs/1411.4028
1. QAOAの骨子
以下にQAOAの要点を記しますが、詳しい内容は追って解説します。
量子断熱計算(QAA)における終状態(最適解を導くハミルトニアン)を$C$、また初期状態(基底エネルギー状態のハミルトニアン)を$B$とします。
ここで、任意の角度パラメータとして、ガンマ($\gamma$)及びベータ($\beta$)を用いて、$C$と$\gamma$に関するユニタリ行列を$U(C,\gamma)$、$B$と$\beta$に関するユニタリ行列を$U(B,\beta)$と定義します。
U(C,\gamma) = e^{-i\gamma C}\qquad(式.1)\\
U(B,\beta) = e^{-i\beta B}\qquad(式.2)
さらに、上記のユニタリ行列を用いた反復計算回数を整数pとし、$(\gamma_1,\gamma_2,...,\gamma_p)$を要素とするベクトルを$\boldsymbol{\gamma}$、$(\beta_1,\beta_2,...,\beta_p)$を要素とするベクトルを$\boldsymbol{\beta}$、p次元の直交基底ベクトルを$|s〉$として、以下の演算子$|\boldsymbol{\gamma},\boldsymbol{\beta}〉$を定義します。
|\boldsymbol{\gamma},\boldsymbol{\beta}〉= U(B,\beta_p)U(C,\gamma_p)U(B,\beta_{p-1})U(C,\gamma_{p-1})...U(B,\beta_1)U(C,\gamma_1)|s〉\qquad(式.3)
次に、上記で定義した演算子$|\boldsymbol{\gamma},\boldsymbol{\beta}〉$を用いて、最適解を導くハミルトニアン$C$の期待値$F_p$を以下のように求めます。
F_p(\boldsymbol{\gamma},\boldsymbol{\beta}) = 〈\boldsymbol{\gamma},\boldsymbol{\beta}|C|\boldsymbol{\gamma},\boldsymbol{\beta}〉\qquad(式.4)
角度パラメータ$\gamma$及び$\beta$を変化させ、$F_p$が取り得る最大値$M_p$を探索します。
M_p = max_{\boldsymbol{\gamma},\boldsymbol{\beta}}F_p(\boldsymbol{\gamma},\boldsymbol{\beta})\qquad(式.5)
最大値$M_p$が求められたとき、その時の$\boldsymbol{\gamma},\boldsymbol{\beta}$が決定し、さらに(式.4)について$C$の期待値が求まると同時に、最適解を与える組合せの状態が求まります。
以上がQAOAの骨子です。
2. 組合せ最適化問題とは
まず初めに、組合せ最適化問題について基本的な知識を確認します。
組合せ最適化問題とは、以下のように言うことができます。
生産活動において、多くの選択肢や組み合わせの中からコスト・成果・利益を最も効率的に上げる選択肢、あるいは最大化(または最小化)させる最良の選択肢を決定すること
例として、交通量最適化問題を取り上げます。
交通量最適化問題とは、道路上の混雑や渋滞をできるだけ軽減するために、各車両のルート選択や配置を適切に行う問題です。
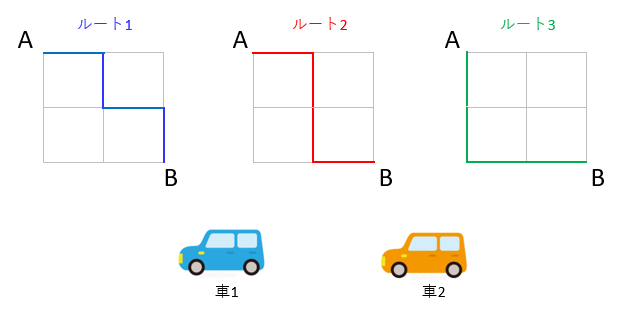
![]() 交通量最適化問題の例題
交通量最適化問題の例題
2台の車、車1と車2があるとします。
2台の車は出発地点Aを同時に出発し、定められたルートを選択して到着地点Bを目指します。
AからBまでのルートは下図のようにルート1、ルート2、ルート3の3通りあり、
車1車2とも好きなルートを選択できるものとします(図1)。
ここで、車1車2とも道路を走行する際に、自分の車だけが道路を走行している時は混雑が無いとみなします。
これに対し、2台の車が同時に同じ道路を走行した場合、混在が発生したとみなします。
混雑が発生しないように2台の車がルートを選択するとき、
どのように選択すれば最も良いかを求めます。
QAOAや量子アニーリングの仕組みを用いて組合せ最適化問題を解く場合、相互作用を及ぼす系でのイジングモデル式を用いて目的関数(コスト関数、エネルギー式、ハミルトニアンとも呼ぶ)を定義し、この目的関数の最大値(または最小値)を求めます。
イジングモデルについての説明はこちらをご参考にして下さい。
![]() Blueqatでナップサック問題を解く一例
Blueqatでナップサック問題を解く一例
https://qiita.com/ttabata/items/537564c90056a6d56879
イジングモデル式の定義は以下となります。
-\sum_{<i,j>}^{}J_{ij}\sigma_i\sigma_j\qquad(式.6)
ここで、$<i,j>$はインデックス$i,j$がすべての相互に異なる組合せを取ることを意味し、$\sigma_i, \sigma_j$はそれぞれの$i,j$要素が+1または-1の二値を取り、その組み合わせの積$\sigma_i\sigma_j$がどのような場合に最大(または最小)になるかを求めます。
この例題ではインデックスをルート1,2,3の3つのルートとし、車1及び車2がそれぞれのルートを選択した場合は1、選択しなかった場合は-1を取ることとします。
また、$J_{ij}$は目的関数を最大または最小にするための調整変数です(重みとも言います)。
一例ですが、この例題では(式.6)を用いて目的関数$M$を以下と定義し、この値が最小値となるルートの組み合わせを探索します。
M = -\sum_{<i,j>}^{}J_{ij}\sigma_i\sigma_j\qquad(式.7)\\
ただし、J_{ij}は以下とする。\\
J_{ij} = \begin{bmatrix} 0 & -1 & 2 \\ -1 & 0 & 2 \\ 3 & -3 & 0 \end{bmatrix}
3. 量子断熱計算(QAA)を引用する
QAOAではユニタリー行列を用いた時間発展計算である**量子断熱計算理論(QAA:Quantum Adiabatic Algorithm)**が応用されていますので、これについて解説します。
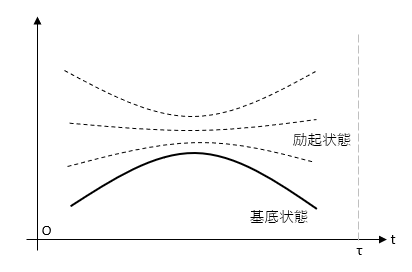
量子断熱計算とは、ある物理系において、外部からの熱の出入りがない状態(エネルギー状態)を保ちながら、時間をかけてゆっくりと状態変化させることを言います。
これを行うことで、初期状態としてのある基底状態を作り出し、これを保ったまま目的の終状態へ変化させることができます。
もし状態変化の速度が速い場合や外部との熱の出入りがある場合、基底状態から励起状態へ変化してしまい、測定ができなくなってしまいます。
量子断熱計算において、この状態遷移は以下のように定式化されます。
H(t)=\frac{t}{\tau}H_0+\bigg(1-\frac{t}{\tau}\bigg)H_{INI}\qquad(式.8)\\
H_0=-\sum_{<i,j>}^{}J_{ij}\sigma_i^{z}\sigma_j^{z}\qquad(式.9)\\
H_{INI}=-\sum_{i=1}^{N}\sigma_{i}^{x}\qquad(式.10)
上記において、$H_{INI}$は初期状態を定めるためのハミルトニアン(エネルギー演算子)、$H_0$は終状態を表すハミルトニアン、そして$H(t)$は初期状態から終状態を導くためのハミルトニアンです。
系の状態は状態ベクトル$|\phi〉$で表され、これらのハミルトニアンを作用させることで具体的な状態ベクトルを求めることができます。
(式.8)に注目してみます。量子断熱計算では初期状態の、ある時刻$t=0$から変化を開始し、最終的に$t=\tau$まで時間を進めます。つまり、$t=0$の時は$H_{INI}$が働き、次第に$\frac{t}{\tau}$項が大きくなり、反対に$(1-\frac{t}{\tau})H_{INI}$項が小さくなり、$t=\tau$の終状態では$H_0$のみが残ります。
$H_{INI}$は初期状態のハミルトニアンで、パウリ行列の$x$成分$\sigma^x$を用いて表現します。
ここで、なぜパウリ行列の$x$成分を用いるかを解説します。
先ほど述べたように、ある系の状態(エネルギー状態)はベクトル$|\psi〉$で表現されます。そして、ある状態を求める場合、$|\psi〉$にハミルトニアンやユニタリー行列$U$を作用させ、その結果得られる固有値を求めるエネルギー値、固有ベクトルをそのエネルギー状態(量子状態)とします。
式で書くと以下のようになります。
H|\psi〉 = E_0|\psi〉\qquad(式.11)\\
|\psi〉\quad...\quad固有ベクトル(量子状態)\\
E_0\quad...\quad固有値(エネルギー値)
ここで、パウリ行列の$x$成分$\sigma^x$の固有ベクトルを求めてみます。
\sigma^x = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}より、\\
\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}|\psi〉=|\psi〉
これを満たすベクトルは、
|\psi〉=\begin{pmatrix} 1 \\ 1 \end{pmatrix}\\
または\\
|\psi〉=\begin{pmatrix} 1 \\ -1 \end{pmatrix}
上記2つです。
どちらのベクトルも直交基底ベクトル
\begin{pmatrix} 1 \\ 0 \end{pmatrix}及び\begin{pmatrix} 0 \\ 1 \end{pmatrix}
の重ね合わせの状態であると言えます。
この重ね合わせ状態は
|\psi〉=|+〉=\frac{1}{\sqrt{2}}(|0〉+|1〉)\\
または\\
|\psi〉=|-〉=\frac{1}{\sqrt{2}}(|0〉-|1〉)
とも表現でき、$z$方向に対しては中間の位置、言わばニュートラルな状態と見ることができます。初期状態$H_{INI}$にパウリ行列の$x$成分を用いる理由は、状態ベクトルをニュートラルな状態に置くためです。
終状態である$H_0$について確認してみます。
終状態のハミルトニアン$H_0$はパウリ行列の$z$成分である$\sigma^z$をかけ合わせた形式となっています。
これは、イジングモデル式の定義と同じ形式をとっており、エドワード・アンダーソンモデルのハミルトニアンと呼ばれます。
H_0=-\sum_{<i,j>}^{}J_{ij}\sigma^z_i\sigma^z_j\qquad(式.12)
ここで先程と同様にパウリ行列の$z$成分についての固有値と固有ベクトルを確認してみましょう。
固有ベクトルを$|\psi〉$、固有値を$E_0$とすると、
\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}|\psi〉=E_0|\psi〉
これを満たす固有値及び固有ベクトルは
固有ベクトルが|\psi〉= \begin{pmatrix} 1 \\ 0 \end{pmatrix}の場合、固有値は1\\
固有ベクトルが|\psi〉= \begin{pmatrix} 0 \\ 1 \end{pmatrix}の場合、固有値は-1
となります。$H_0$についてインデックスi,jを展開すると以下となることから
H_0=-J_{12}\sigma_1^z\sigma_2^z-J_{13}\sigma_1^z\sigma_3^z-J_{14}\sigma_1^z\sigma_4^z...
各インデックスi,jそれぞれにおいて、固有値が1または-1となり、状態ベクトルも定まります。このことを利用し、イジングモデル式で$\sigma_i$及び$\sigma_j$が±1どちらを取るかの組み合わせを決めたのと同様に、パウリ行列の$z$成分と固有値(±1どちらかを取る)及び固有ベクトルを利用することで、終状態の状態ベクトルを定め、最終的に組合せ最適解を導くことができます。
4. 量子断熱計算を用いてQAOAを定義する
それでは、冒頭「1. QAOAの骨子」で記述したQAOAの定義について細かく再定義します。
量子ゲートに関する理論では、一般に量子状態がある状態$|\psi〉$から別の量子状態$|\psi'〉$へ変化した場合、その変化はユニタリー行列演算子$U$を用いて、
|\psi'〉=U|\psi〉
と表現します。これをユニタリー発展と言います。
例えば、量子断熱計算のような時間軸tに関してユニタリー発展を考えた場合、これを特に時間発展と呼び、以下のように表現します。
|\psi'(\tau)〉=U(\tau,0)|\psi(0)〉\qquad(式.13)\\
0≦t≦\tau
上記の$U(\tau,0)$は時刻$t=0$から$t=\tau$までの変化を一つのユニタリー行列$U$で書いたものです。全体時間$\tau$を小さな時間区間$Δt$に分割した場合、以下のように書き表すことができます。
U(\tau,0)=U(\tau,\tau-Δt)U(\tau-Δ,\tau-2Δ)...U(Δt,0)\qquad(式.14)
ここで任意の微小区間$(l+1)Δt ~ lΔt$($l$は整数)において、以下の近似を行います。
U\big((l+1)Δt,lΔt\big)\cong e^{-iΔtH(lΔt)}\qquad(式.15)
ここで用いたハミルトニアンは量子断熱計算で定義した(式.8)の$H$を引用します。また、これに加えて量子力学の基本法則であるシュレーディンガー方程式に従うことから、このような指数関数の形式で書き表されます。
ハミルトニアン$H$の内容を確認しましょう。$H$は冒頭に定義した初期状態のハミルトニアン$B$、及び終状態のハミルトニアン$C$を用いて、次のように記述できます。
H=\frac{t}{\tau}C+\bigg(1-\frac{t}{\tau}\bigg)B\qquad(式.16)
$C$は終状態のハミルトニアンで、組合せ最適化問題の解となる状態ベクトルを導く役割を持つため、(式.9)より、
C=-\sum_{<i,j>}^{}J_{ij}\sigma_i^z\sigma_j^z\qquad(式.17)
です。また$B$はニュートラルな初期状態を表すハミルトニアンのため、以下のように
B=-\sum_{i=1}^{N}\sigma_i^z\qquad(式.18)
となります。
(式.15)で近似したハミルトニアン$H$に(式.16)を代入します。
U\big((l+1)Δt,lΔt\big) \cong e^{-iΔtH(lΔt)}\\
=e^{-iΔt \big\{ \frac{lΔt}{\tau}C+\big(1-\frac{lΔt}{\tau}\big)B \big\} }\qquad(式.19)
上式の$e$の指数部分に注目します。
(式.19)の$C$や$B$はハミルトニアン演算子であることから、単純に以下のように指数を分離することはできないことに注意が必要です。
e^{B+C}=e^{B}c^{C}
よって、ここでリー・トロッター積公式[参照]を引用し、次のように変形(近似)します。
(式.19)=\bigg\{ e^{-\frac{i}{p}Δt\big(\frac{lΔt}{\tau}\big)C}e^{-\frac{i}{p}Δt\big(1-\frac{lΔt}{\tau}\big)B} \bigg\}^{p}\qquad(式.20)
上式について、
\gamma=\frac{1}{p}Δt\bigg(\frac{lΔt}{\tau}\bigg)\\
\beta=\frac{1}{p}Δt\bigg(1-\frac{lΔt}{\tau}\bigg)\\
とおくと、次のように変形できます。
(式.20)=\bigg\{e^{-i\gamma C}e^{-i\beta B}\bigg\}^{p}\qquad(式.21)
以下の通り、冒頭の定義(式.1)(式.2)を用いて
U(C,\gamma)=e^{-i\gamma C}\qquad(式.1)\\
U(B,\beta)=e^{-i\beta B}\qquad(式.2)\\
(式.21)=\bigg(U(B,\beta)U(C,\gamma)\bigg)^p
各区間$Δt$を1,2,3,...,pに分けると
(式.21)=U(B,\beta_p)U(C,\gamma_p)U(B,\beta_{p-1})U(C,\gamma_{p-1})...U(B,\beta_1)U(C,\gamma_1)\qquad(式.22)
上式が(式.3)の根拠となります。
(式.20)でリー・トロッター積公式を用いて変形(近似)を行いましたが、この変形(近似)において、$p→∞$とすることで精度が上がります。すなわち、(式.3)の繰返し計算の回数pを増やすことで精度が向上すると言えます。
演算子$|\boldsymbol{\gamma},\boldsymbol{\beta}〉$を再定義します。
|\boldsymbol{\gamma},\boldsymbol{\beta}〉= U(B,\beta_p)U(C,\gamma_p)U(B,\beta_{p-1})U(C,\gamma_{p-1})...U(B,\beta_1)U(C,\gamma_1)|s〉\qquad(式.23)\\
ただし、p→\inftyに近づけると精度が向上する
以上がQAOAの理論の解説になります。
次はQAOAの実践編、プログラミングに入ります。
 QAOAのプログラミング【実践編】
QAOAのプログラミング【実践編】
ここではQAOAのプログラミング実装例をご紹介します。
プログラミングには、量子コンピュータ・シミュレータとして評価の高い、blueqat株式会社(東京・本郷)が提供するblueqat(ブルーキャット)を使用します。
今回使用したblueqatのバージョンは0.3.18です。
![]() blueqat (https://blueqat.com/)
blueqat (https://blueqat.com/)
1. 問題の定式化
理論編で例題として挙げた問題をもう少し詳しく解説します。
下図(図2)のように、二次元格子平面上に道路を表現します。
ここで点は交差点、点と点に挟まれた辺を一つの道路とします。
図の通り、ルート1(青)とルート2(赤)は二か所の道路で、またルート2(赤)とルート3(緑)は一か所の道路で重なり部分があり、混雑が発生していることがわかります。
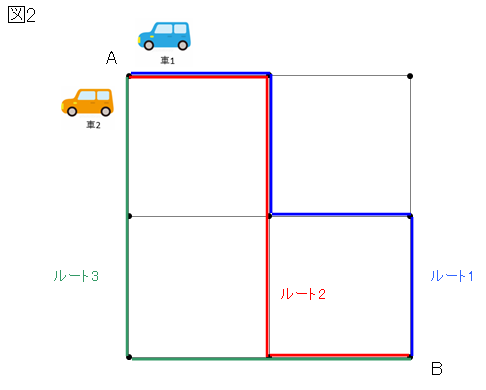
今回の例題を解くにあたり、この道路の重なり部分(混雑)をどのように評価(目的関数の最小化)するかを仕組化し、解を求めることになります。
組合せ最適化問題を解くにあたり、一般的な手法として、それぞれの組み合わせを採用するかしないかを0,1で表すことがあります。今回もこの手法をとることにします。
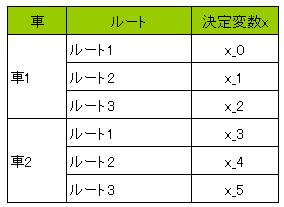
この0,1について、0は組み合わせを取らないケース、1は組み合わせを取るケースとします。この0,1を取る変数を$x$とし、決定変数と呼びます。
例題では$x$を6つ用意し、車1がルート1を取るか取らないかを$x_0$、ルート2を取るか取らないかを$x_1$、ルート3を取るか取らないかを$x_2$とし、同様に車2についてもルート1,2,3について決定変数$x_3$,$x_4$,$x_5$を用意します。まとめると下表となります。
ここで目的関数を作成するにあたり、道路の混雑具合を評価する基準(方法)を考えます。
例題では、ルート1とルート2は一か所の道路で重なっているため、混雑度を1とします。また、ルート2とルート3は二か所で重なっているため混雑度2とします。ルート1とルート3の混雑度は0です。この混雑度を変数$J_{ij}$で表し、重みと呼ぶことにします。iは車1が取るルートの決定変数のインデックスを、jは車2が取るルートの決定変数のインデックスとすると、重み変数$J_{ij}$は以下とすれば良いことがわかります。
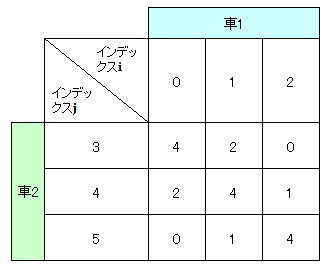
J_{ij}=\begin{pmatrix} 4 & 2 & 0 \\ 2 & 4 & 1 \\ 0 & 1 & 4 \end{pmatrix}\qquad(式.24)
これらを用いて、(式.7)に従って目的関数を作成します。
\begin{align}
M&=-\sum_{i=0,j=3}^{2,5}J_{ij}x_ix_j\\
&=-(J_{03}x_0x_3+J_{04}x_0x_4+J_{05}x_0x_5+J_{13}x_1x_3+J_{14}x_1x_4+J_{15}x_1x_5+J_{23}x_2x_3+J_{24}x_2x_4+J_{25}x_2x_5)\\
&=-(4x_0x_3+2x_1x_3+2x_0x_4+4x_1x_4+x_2x_4+x_1x_5+4x_2x_5)
\qquad(式.25)
\end{align}
ここで以下の注意が必要です。
(式.7)では$\sigma$が取る値が±1でしたが、(式.25)では0,1を取る決定変数$x$を使用しています。
イジングモデル式では一般的に上記のように±1としますが、以下の式を用いると±1を0,1に変換することができます。
x=\frac{\sigma-1}{2}
このように、最適化問題を解くにあたっては組み合わせを採用するかしないかを表す変数を0,1として扱った方が扱いやすく、式も立てやすいため、上式でもこのようにしています。
$\sigma$と$x$の関係は一次式で定数倍および定数項の付加のみであるために、同じ性質を持つ式としてみなして良く、目的関数は(式.25)とします。
目的関数をこのように条件に合わせて具体的に式に書き表わすことを定式化と呼びます。
今回の定式化ではさらにもう一つの条件の追加が必要です。
車1はルート1,2,3を同時に3つ取れないので以下が成り立ちます。
x_0+x_1+x_2=1
同様に車2についても同じように、
x_3+x_4+x_5=1
このような、解く問題に応じた特定の条件を制約条件と言います。
制約条件項を以下のようにして目的関数に取り込みます。
\begin{align}
制約条件項&=-\bigg\{\bigg(\sum_{i=0}^{2}x_i-1\bigg)^2+\bigg(\sum_{j=3}^{5}x_j-1\bigg)^2\bigg\}\\
目的関数\quad M&=-\sum_{i=0,j=3}^{2,5}J_{ij}x_ix_j-k\bigg\{\bigg(\sum_{i=0}^{2}x_i-1\bigg)^2+\bigg(\sum_{j=3}^{5}x_j-1\bigg)^2\bigg\}\\
&=-(4x_0x_3+2x_1x_3+2x_0x_4+4x_1x_4+x_2x_4+x_1x_5+4x_2x_5)-k\bigg\{(x_0+x_1+x_2-1)^2+(x_3+x_4+x_5-1)^2\bigg\}
\end{align}
kはバイアス変数で、解が得られるように必要に応じて適切な値を設定します。
また、決定変数$x$は0,1を取ることから、$x^2$もまた0,1を取ることがわかります。
よって、以下のように取り扱います。
x_i^2=x_i
上式を展開し、整理すると以下のようになります。
M=-4x_0x_3-2x_1x_3-2x_0x_4-4x_1x_4-x_2x_4-x_1x_5-4x_2x_5\\
-k(-x_0-x_1-x_2+2x_0x_1+2x_0x_2+x_1x_2\\
-x_3-x_4-x_5+2x_3x_4+2x_3x_5+2x_4x_5)\qquad(式.26)
定式化の結果、(式.26)が得られました。
2. blueqatのプログラミング
blueqatにはQAOAの理論に基づくパラメータ計算を自動的に行うとても便利な機能が備わっており、プログラムを簡潔に書くことができます。
特に、【理論編】で示した(式.23)の計算や角度パラメータを内部的に計算する仕組みがあり、これを**ansatz(アンザッツ)**と呼びます。
プログラマーはansatzの働きを意識することなく、定式化のコーディングに専念できる点が優れています。
(式.26)より、本例題のコーディングは以下となります。
from blueqat import vqe
from blueqat.pauli import qubo_bit as x
# バイアス変数
k = 2.0
# 目的関数
M = 4 * x(0) * x(3) + 2 * x(1) * x(3) + 2 * x(0) * x(4) + 4 * x(1) * x(4) + x(2) * x(4) + x(1) * x(5) + 4 * x(2) * x(5) + k * (-1 * x(0) - x(1) - x(2) + 2 * x(0) * x(1) + 2 * x(0) * x(2) + 2 * x(1) * x(2) - x(3) - x(4) - x(5) + 2 * x(3) * x(4) + 2 * x(3) * x(5) + 2 * x(4) * x(5) + 2)
# 繰返し計算回数(p)
step = 20
# QAOA計算を実行
result = vqe.Vqe(vqe.QaoaAnsatz(M, step)).run()
# 結果を表示
print(result.most_common(5))
ここでは、バイアス変数を2.0としました。
また、繰り返し回数は20としています。繰り返し回数を増やすと精度が向上すると考えられますが、計算の所要時間も長くなってしまいます。試行実行しながら適度な数字を設定します。
3. 結果の検証
最後に、blueqatで算出した解が適切な解であるかどうかを確認します。
プログラムの実行結果は以下となりました。
<実行結果>

プログラム中の「most_common(5)」メソッドで上位5件を表示しました。
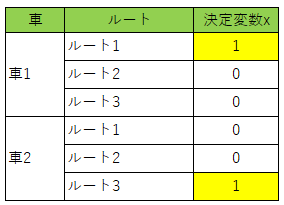
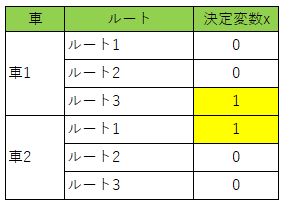
結果のデータが5件表示されていて、「(1, 0, 0, 0, 0, 1)」の部分は決定変数$x_0$~$x_5$の値を示しています。
また、小数部分「0.209896...」は、その決定変数による組み合わせの解が全体の解のどのくらいの割合で算出されたかを示しています。
割合の値が最も大きいケースが最適解となります。
今回の計算では、上位2件が同じ割合となりました。つまり、解が2つあることになります。
決定変数の値と車1及び車2が取るべきルートを見てみると、以下の2パターンが解であることがわかります。黄色部分が解です。
まとめると、車1がルート1を選択した場合は車2がルート3を、車1がルート3を選択した場合は車2がルート1を選択すれば良いことがわかります。
以上で、QAOAによる組合せ最適解問題を解くことができました。
 関連情報
関連情報
![]() A Quantum Approximate Optimization Algorithm
A Quantum Approximate Optimization Algorithm
(by Edward Farhi, Jeffrey Goldstone, Sam Gutmann)
https://arxiv.org/abs/1411.4028
![]() 【ほぼ決定版】量子コンピュータVQE/QAOAセミナーまとめ
【ほぼ決定版】量子コンピュータVQE/QAOAセミナーまとめ
https://qiita.com/YuichiroMinato/items/3f68b9fed67ff3a01370
![]() 量子コンピュータ・シミュレータ blueqat (blueqat株式会社)
量子コンピュータ・シミュレータ blueqat (blueqat株式会社)
https://blueqat.com/
![]() Blueqatでナップサック問題を解く一例
Blueqatでナップサック問題を解く一例
https://qiita.com/ttabata/items/537564c90056a6d56879
 ご意見など
ご意見など
ご意見、間違い訂正などございましたらお寄せ下さい。