More than 3 years have passed since last update.

Blueqatでナップサック問題を解く一例

Last updated at 2020-08-28Posted at 2020-05-06

この記事の目的

組合せ最適化問題の代表的な問題の一つであるナップサック問題を、量子アニーリングで解く方法を確認します。量子アニーリングで解いた解と、組合せ最適化問題で一般的に使用されるソルバーで解いた解を比較し、その解の妥当性を評価します。
量子アニーリングにはMDR社のオープンソースフレームワークであるBlueqatを使用します。

ナップサック問題について

ナップサック問題については、以下に説明を記載しました。

■GoogleのOR-Toolsでナップサック問題を解く - 組合せ最適化問題の基礎を実践
https://qiita.com/ttlabo/items/bcadc03004418f32f49d

今回の問題はこちらを使用します。こちらはGoogleからフリーで提供されているソルバーのOR-Toolsで解いた例題です。ここで解いた解と今回Blueqatで解いた解を用いて、両者を比較します。

検証環境

今回の検証環境は以下です。

Python 3.7.3
Blueqat 0.3.13

Blueqatについて

Blueqatは、量子コンピュータのアプリケーション・ミドルウェアとハードウェアの開発を行っているMDR株式会社から提供されている、オープンソースの量子コンピューティング・シミュレーターです。Python言語で動作します。

Blueqatの使用方法は、チュートリアルなどが参考になります。

■Blueqat 0.3 開発メモ
https://qiita.com/gyu-don/items/9db7a585a126ffd1b994

■Blueqatのドキュメントへようこそ!
https://blueqat.readthedocs.io/ja/latest/

イジング模型について

量子アニーリングで組合せ最適化問題を解く際には、解決する問題をイジング模型(Ising Formulation)と呼ばれる数式に当てはめて解を求めます。

イジング模型について説明します。
まず、イジング模型(またはイジングモデル)とは、物理学の一つの統計力学において定義される模型で、相互作用をする多体系を記述する基本的な模型です。Wikipediaによると、1920年にドイツの物理学者のヴィルヘルム・レンツ(Wilhelm Lenz)によって提案されたとされています。イジング模型の名は、レンツの指導学生だったエルンスト・イジング(Ernst Ising)から取られました。

相互作用する多体系とは、原子や電子などの量子的な世界において働く作用で、その粒子間の相互作用は電気抵抗や熱伝導など個体の輸送現象における散乱や緩和の原因となるとともに、気相(気体)～液相(液体)転移、強磁性相転移、超電導転移などの相転移現象を引き起こす原因でもあります。相転移とは、例えば気体が圧縮・冷却によって凝縮を起こす現象や、常磁性体がキュリー点以下まで温度を下げると強磁性体になる現象です。常磁性体とは、ある物質を磁場中に置くと原子の磁気モーメント(磁石のNS極のような方向性を持つもの)が磁場の向きにそろい、磁場と平行な向きに磁化が起こるような物質です。強磁性体とは外部から磁場が加わらなくても磁化を持つ物質です。

イジング模型は多体問題を取り扱う模型として、磁性体の磁気的性質を記述したり、二元合金や気体の凝縮を取り扱う格子気体、さらに生体内のポリペプチドやDNAの転移・融解を記述する際にも応用されます。

イジング模型の数式を考えるにあたり、まず粒子または系の構成要素が独立で相互作用がない場合を考えると、この系が保持する物理的なエネルギー単位のハミルトニアンHは以下となります。

H\;=\;\sum_{i=1}^{N}H_i\\
ここで、iは粒子の番号で、全部でN個とする。

一方、粒子同士の相互作用がある系のハミルトニアンHは一般に、

H\;=\;\sum_{i=1}^{N}H_i\;+\;\sum_{ij}H_{ij}\\

と表されます。
第2項目はi番目の粒子とj番目の粒子の相互作用です。

特に最も典型的な模型である磁性体におけるイジング模型を例にとると、イジング模型は、

H\;=\;-J\sum_{〈ij〉}^{}s_{zi}s_{zj}\;+\;\mu_B\mathcal{H}\sum_{i=1}^{N}s_{zi}\\

で表されます。イジング模型の構造やそれぞれの定数は以下のように定義されます。
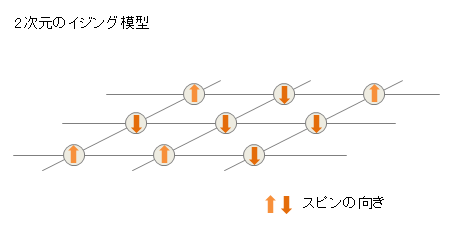
ここで、イジング模型では2次元平面上で磁性体の結晶が下図の格子面の交点に乗っていて、z方向に磁場がかかっているとします。

J_{ij}\;…\;交換積分でi,jのスピン間の距離のみに依存し、通常は隣接するスピンの組み合わせを表す。\\
強磁性相互作用なら正、反強磁性相互作用なら負となる。\hspace{50pt}\\
s\;…\;磁気モーメントの向きを表し、+1または-1のスピンと呼ばれる値をとる。\hspace{15pt}\\
\mu_B\;…\;スピンの磁気モーメントの単位でボーア磁子と呼ぶ。\hspace{90pt}\\
\mathcal{H}\;…\;磁場を表す。\hspace{180pt}\\

ここで大切なことは、イジング模型において隣接するスピン(磁気モーメントの向きを表す値)の向きが同じ向きに揃うとき、エネルギー(ハミルトニアンH)が低い状態になるということです。
絶対0度のような極低温では、スピンが揃ってエネルギーを下げようとし、スピンが揃った状態(強磁性状態)が出現します。

量子アニーリングにおいて、D-Wave System社の実機などでは、量子コンピューティングを実現する基本素子の量子ビットが互いに結合し合い、上記の磁性体のイジング模型で定義されたエネルギーが最も低い状態(基底状態)を保つように設計されています。
今回はあくまでシミュレーターのBlueqatを使用しますが、原理はこれと同じです。

イジング模型による定式化

組み合わせ最適化問題においては、上述のイジングモデルを応用し、求める目的関数の値が最も大きく(あるいは小さく)なる際のスピンの組み合わせを探索することで実際の解を求めようとする試みです。

組み合わせ最適化問題とは、離散値を取る複数の変数について、それらの値のうちいくつかを組み合わせて、求める問題のコストや効果または期待値などの目的関数を全体的に最大化または最小化する(最適化する)問題です。
この組み合わせにおいて、それぞれの要素を採用するか否かの切り分けを0または1の変数で保持し、1の場合は採用し0の場合は採用しないという規則のもとに最も理想的な解を0または1の組み合わせで表現しますが、この0または1の切り分けと目的関数をイジング模型に応用し、このイジング模型を用いて自然物理的にあるいは量子力学的に解を探索する技術が量子アニーリングとなります。
ここで捕捉ですが、イジング模型ではスピンを+1,-1としますが、量子アニーリングでは量子ビットと呼び0,1とします。この値の違いは数式上の表現の違いだけであり、本質的には等価です。組み合わせ最適化問題では、実社会問題に即して使用しやすいように0,1を採用します。

組み合わせ最適化問題では、イジング模型と目的関数のハミルトニアンHを以下の式で表します。

H(\sigma)\;=\;-\sum_{〈ij〉}^{}J_{ij}\sigma_i\sigma_j\;-\;\sum_{i=1}^{N}h_i\sigma_i\hspace{30pt}式(1)\\
〈ij〉…重複を除き、全てのi,jの組み

σ(シグマ)は変数の組み{σ1,σ2,σ3,...,σN}で、各σは0,1を取ります。
上記式の〈ij〉はi,jとj,iは同じ組みとみなし二重に計算しないという意味です。
相互作用と局所磁場を表す定数の組み{Jij, hi}が与えられたときにハミルトニアンH(σ)を最小にするσを求めます。

組み合わせ最適化問題を解く際に、その手順として一般的に定式化というものを行います。
定式化では、解くべき問題についての様々な条件(制約条件)を数式で与えます。
量子アニーリングでは、この定式化においてアンドリュー・ルーカス氏(Andrew Lucas)から「Ising formulations of many NP problems」というタイトルで参考となる論文が発表されています(リンクは出典欄に記載)。

今回のナップサック問題でも、この論文にある数式を利用して問題を解きます。
今回のナップサック問題について、以下に諸条件をまとめます。
※この問題では荷物の重さの代わりに体積を条件としています。

荷物の数　N個\\
荷物のラベル(番号)　1,2,3,...,α\\
荷物の体積　w_α\\
荷物の価値　c_α\\
ナップサックの最大許容容量　W_{max}\\
決定変数　x_α　(α番目の荷物を詰めるかどうかの判定)\\
荷物の総体積　W = \sum_{α=1}^{N}w_αx_α\\
荷物の総価値　C = \sum_{α=1}^{N}c_αx_α

ここで、式(1)では0,1を取る変数をσとしていますが、数式計算する上で慣れ親しんでいるxを使用します。xは決定変数と呼ばれ、組み合わせにおいてそれぞれの要素を取るか取らないかを0,1で決める変数です。
求めるべき目的変数は、条件 (W ≦　Wmax) を満たす上での総価値Cで、これが最大になることです。

論文を参考に、ナップサック問題における制約条件の定式化は以下とします。

H\;=\;H_A\;+\;H_B\hspace{20pt}式(2)\\
H_A\;=\;A\bigg(1-\sum_{n=1}^{W}y_n\bigg)^2\;+\;A\bigg(\sum_{n=1}^{W}ny_n - \sum_{α}^{}w_αx_α\bigg)^2\hspace{20pt}式(3)\\
H_B\;=\;-B\sum_{α}^{}c_αx_α\hspace{20pt}式(4)\\
但し、定数A,Bについては以下を満たすものとする。\\
0 < Bmax(c_α) < A\hspace{20pt}式(5)

上記制約式について解説します。
ハミルトニアンHはHAとHBの2つから求められます。

まず、HAについて見てみます。
ここで、ynという新たな変数を使用します。
ynは0または1を取る変数(バイナリー変数)とし、荷物n=1～αの組み合わせについてナップサックの総体積がynになるかどうかを表現します。
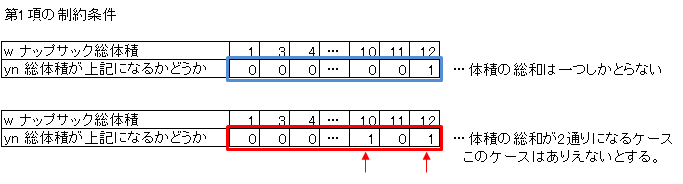
今回の問題では、ナップサックの容量が12なので、例えば以下のようになります。

式(3)第1項は、ynの和が1を取るとします。下表の通り、ynは総体積が一つだけに決まるという制約を付けます。Aは定数ですが、実際には値は求めません。

次に第2項について、nynの総和は荷物の体積の総和であるとします。
第1項にも関連しますが、nynは下表のようにナップサックの体積とyn値の積で、ynは一つだけが1でその他は0となるため、nynの和はナップサックの荷物の体積の総和のどれかの一つに決まるという意味です。

ここで、ナップサックの荷物の体積の総和(荷物の総体積)は以下で求められます。

W = \sum_{α=1}^{N}w_αx_α\\
　= w_1x_1 + w_2x_2 + w_3x_3 + … + w_nx_n

xnは0,1を取る決定変数で、n番目の荷物をナップサックに詰めるかどうかを決める変数なので、例えば下表のように荷物C,D,Eを選択すれば総体積を12にすることができます。

HAに関する制約式に見る通り、実際のところHAは値が0となることが条件です。

次に、HBについて見てみます。

ここでは、アイテムの価値の総和(荷物の総価値)に-(マイナス)をかけているので、負の方向に最も大きくなる(HBが最小化する)ようなxの組み合わせを求めています。
上記の荷物の総体積=12の例では、荷物C,D,Eを選択しましたが、この選択は他にも候補があり、例えば以下のように荷物A,B,Eを選択することも可能です。この場合は荷物の総価値が-17となります。

決定変数xαをどのような取るかは、イジング模型におけるハミルトニアン(H = HA + HB)が最小となるように量子アニーリングが計算し、決定します。

最後に、論文では定数A,Bの取り得る値について定義しています。
荷物のうち最も価値が大きい値は8なので、max(cα)=8としてBについて式を整理すると、

B < \frac{A}{8}

となるため、今回の計算では

B = \frac{A}{9}\hspace{20pt}式(6)

として計算します。

定式化後、式を展開しQUBOマトリックスを求める

Blueqatで組み合わせ最適化問題を解く際には、定式化した数式からQUBO行列(QUBOマトリックス)を求め、これをBlueqatにプログラミングして解を求めます。

現在のBlueqatは量子ゲート計算と量子アニーリング計算の両方の機能を持っていますが、もともとは量子ゲート計算用のフレームワークで、量子アニーリング計算はWildqatにその機能が含まれていました。QUBOの詳細については、Wildqatのチュートリアルにて確認できます。

■Wildqatのドキュメントへようこそ!
https://wildqat.readthedocs.io/ja/latest/

さっそく式(3)、式(4)を式(2)に代入して展開します。
ここで、nが取り得る値は1,3,4,5,6,7,8,9,10,11,12です。

H\;=\;H_A\;+\;H_B\hspace{240pt}\\
=\;A\bigg(1-\sum_{n=1}^{12}y_n\bigg)^2+A\bigg(\sum_{n=1}^{12}ny_n- \sum_{α=1}^{5}w_αx_α\bigg)^2-B\sum_{α=1}^{5}c_αx_α\\
=\;A\bigg(1-y_1-y_3-y_4-y_5-y_6-y_7-y_8-y_9-y_{10}-y_{11}-y_{12}\bigg)^2\\
+A\bigg(y_1+3y_3+4y_4+5y_5+6y_6+7y_7+8y_8+9y_9+10y_{10}+11y_{11}+12y_{12}\\
-w_1x_1-w_2x_2-w_3x_3-w_4x_4-w_5x_5\bigg)^2\\
-B\bigg(c_1x_1+c_2x_2+c_3x_3+c_4x_4+c_5x_5\bigg)\hspace{20pt}式(7)

上記の式を愚直に展開すると項が増えて煩雑となりますので、次のような工夫を取り入れて、より簡単にします。

まず、今回は量子アニーリングの解法の一例として、ナップサックの総体積が容量と等しい値の12であることを仮定して解を求めます。
すなわち、y1=0,y3=0,y4=0,y5=0,y6=0,y7=0,y8=0,y9=0,y10=0,y11=0とします。(y2はアイテムにありません)
ただし、本来はナップサックの体積の和をそれぞれのアイテムの組み合わせごとに計算して、どれが最も妥当かを検証するところまでを含める必要があります。

また、式(6)より、B=A/9とします。
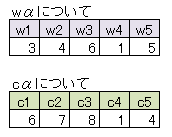
w1～w5及びc1～c5は問題により与えられていて、以下です。

式(7)について、第1項は0となることが明らかです。
これらを考慮し、式(7)を以下に整理します。

式(7)\;=\;A\bigg(0\bigg)^2 + A\bigg(12×1-3x_1-4x_2-6x_3-1x_4-5x_5\bigg)^2\\
-\frac{A}{9}\bigg(6x_1+7x_2+8x_3+1x_4+4x_5\bigg)\\
=\;\frac{A}{9}\lbrace\:9(12-3x_1-4x_2-6x_3-1x_4-5x_5)^2\\
-(6x_1+7x_2+8x_3+1x_4+4x_5)\:\rbrace\hspace{20pt}式(8)

ここからさらに式を展開しますが、ここで次の工夫を取り入れます。
xは0,1のいずれかを取る変数なので、2乗してもやはり0,1です。
よって、以下が成立します。

x_1^2 = x_1\\
x_2^2 = x_2\\
x_3^2 = x_3\\
x_4^2 = x_4\\
x_5^2 = x_5

これらを取込むと、式(8)は

式(8)\;=\;\frac{A}{9}\bigg(1296-573x_1-762x_2-1020x_3-213x_4-879x_5\\
+216x_1x_2+324x_1x_3+54x_1x_4+270x_1x_5\\
+432x_2x_3+72x_2x_4+360x_2x_5+108x_3x_4\\
+540x_3x_5+90x_4x_5\bigg)\hspace{20pt}式(9)

上式より、QUBOマトリックス(Qij)は以下となります。

式(9)\;=\;C\sum_{i}^{}\sum_{j}^{}Q_{ij}x_ix_j\;+\;D\\
Q_{ij}\;=\;\begin{pmatrix} -573 & 216 & 324 & 54 & 270 \\\
0 & -762 & 432 & 72 & 360 \\\
0 & 0 & -1020 & 108 & 540 \\\
0 &  0 & 0 & -213 & 90 \\\
0 & 0 & 0 & 0 & -879 \\\
\end{pmatrix}

ここで、C及びDは定数ですが求める必要はありません。

Blueqatのプログラミングとその解

Blueqatで実装する際に、前節で求めたQUBOマトリックスを使用します。
以下、Blueqatのプログラムを掲載します。

knapsack.py

import blueqat.opt as wq                   # … (1)

a = wq.opt()                               # … (2)
a.qubo = [
    [-573,  216,   324,   54,  270],
    [   0, -762,   432,   72,  360],
    [   0,    0, -1020,  108,  540],
    [   0,    0,     0, -213,   90],
    [   0,    0,     0,    0, -879]]       # … (3)
    
result = a.sa(shots=200,sampler="fast")    # … (4)
z = wq.counter(result)

print(z)                                   # … (5)

プログラミングは以上です。
順を追って解説します。

(1) Blueqatをimportします。
(2) 最適化計算を行うためのオブジェクト変数を宣言します。
　変数名はaをとします。
(3) aに対してQUBOをセットします。
　セットする行列は上三角行列とします。(左上から右下へ対角線上の下部を0とする)
(4) 最適化計算を実行します。Blueqatの内部では、イジング模型の理論に基づきハミルトニアンが最小となるように計算が行われ、決定変数x1～x5それぞれの0,1の値が決定します。
ここでは、パラメータshots,samplerを以下のように設定しています。

　shots　…　計算回数です。量子コンピューティングでは一般的に複数回計算を行います。
　sampler　…　量子シミュレーション(焼きなまし温度処理)における工程の回数を指定します。設定値には"fast"と"normal"があり、"fast"の場合は100、"normal"の場合は1000に設定されます。

(5) 処理結果を表示します。

今回の計算結果、以下の解が得られました。

Counter({'11001': 60, '11100': 50, '00111': 46, '01110': 44})

量子コンピューティングでは複数回の計算を行うため、異なる結果が複数得られます。
そしてそれらの解がそれぞれどの程度の割合で出現するかを確率で表現します。

今回の計算で得られた解は、決定変数x1～x5の候補が以下のパターンであり、それぞれの確立を見てどれが最もふさわしい解かを選択します。
※60,50,46,44は、200回計算を行った解の内訳を意味します。

パターン	x1	x2	x3	x4	x5	確率
解①	1	1	0	0	1	30%(60回)
解②	1	1	1	0	0	25%(50回)
解③	0	0	1	1	1	23%(46回)
解④	0	1	1	1	0	22%(44回)

上記から、最も良い解は解①の60%とすればよいことが分かります。
よって、今回のナップサック問題は以下が解答になります。

ナップサック問題の解答

選択するアイテム
　A,B,E
体積の和
　3 + 4 + 5 = 12
価値の和
　6 + 7 + 4 = 17

さらに、上記の解が組合せ最適化問題で一般的に使用されるソルバーで解いた解と同じであることが確認できました。

出典

■参考テキスト
　「量子アニーリングの基礎」　西森秀稔・大関真之[著]　共立出版

■参考論文
　Ising formulations of many NP problems
　https://www.frontiersin.org/articles/10.3389/fphy.2014.00005/full

ご意見など

ご意見、間違い訂正などございましたらお寄せ下さい。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up