この記事は古川研究室 Workout_calendar 17日目の記事です.
本記事は古川研究室の学生が学習の一環として書いたものです.内容が曖昧であったり表現が多少異なったりする場合があります.
概要
第1回目は,最尤推定を用いた回帰の記事でした.第2回目である本記事では,MAP推定を用いた回帰についてまとめたいと思います.
この記事で行ったことは以下になります.
- (理論)MAP推定を用いたモデルのパラメータ$\mathbf{w}$の導出
- (実装)MAP推定を用いた回帰のスクラッチ実装
MAP推定による回帰のタスク設定
与えられているもの
入力$\mathbf x=(x_1,...,x_N), x\in\mathbf R$と出力$\mathbf y=(y_1,...,y_N), y\in\mathbf R$のデータセット
仮定
・$\mathbf x$と$\mathbf y$のデータセットは,独立同分布(i.i.d.)に従うとします.
・$y_i,f,\epsilon$を次のように仮定します($\beta$はガウスノイズの精度でスカラーです).
\begin{eqnarray}
y_i&=&f(x_i;\mathbf w)+\epsilon_i
\end{eqnarray}
\begin{eqnarray}
f(x_i;\mathbf w)=\mathbf{w}^T\boldsymbol{\phi}(x_i)
\end{eqnarray}
\begin{eqnarray}
\epsilon_i&\sim& N(0,\beta^{-1})
\end{eqnarray}
$;;;$ここで,基底関数$\boldsymbol{\phi}(x)$とパラメータ$\mathbf{w}$は$D$個あるので次のようになります.
\begin{eqnarray}
\boldsymbol{\phi}(x_i)&=&(\phi_1(x_i),...,\phi_{D}(x_i))^T
\end{eqnarray}
\begin{eqnarray}
\mathbf{w}&=&(w_1,...,w_{D})^T
\end{eqnarray}
・事前分布は,あまり大きな$\mathbf w$を取らないと仮定します(ハイパーパラメータ$\alpha$はガウス分布の精度でスカラーです).
$$p(\mathbf w|\alpha)=N(\mathbf w|\mathbf 0,\alpha^{-1}\mathbf I)$$
MAP推定のタスク
事後分布が最大となるパラメータ$\mathbf w_{MAP}$を推定します.
\begin{eqnarray}
\mathbf {w}_{MAP}
&=&\underset{\mathbf{w}}{\arg \max\;}p(\mathbf y|\mathbf x,\mathbf w,\beta)p(\mathbf w|\alpha)\\\
\end{eqnarray}
推定した$\mathbf w_{MAP}$から,新規入力$x^*$に対する出力$y^*$を予測できます.
解析解の導出
-
事後分布を最大化するパラメータ$\mathbf{w}_{MAP}$を求める
1-1 尤度と事前分布から変形して目的関数を求める
1-2 目的関数を$\mathbf{w}$で偏微分して,極値を求める -
$\mathbf{w}_{MAP}$を用いて,新規入力$x^$に対する出力$y^$を予測する
1. 事後分布を最大化するパラメータを求める
1-1 尤度と事前分布から変形して目的関数を求める
MAP推定が最尤推定と異なる点は,ベイズ的アプローチである事前分布を使用できることです.ここで,事前分布$p(\mathbf{w}|\alpha)$はあまり大きな$\mathbf{w}$を取らないガウス分布と仮定すると,
\begin{eqnarray}
p(\mathbf{w}|\alpha)
&=&N(\mathbf{w}|\mathbf 0,\alpha^{-1}\mathbf I)\\
&=&\left(\frac{\alpha}{2\pi}\right)^{\frac{D}{2}}\exp\left(-\frac{\alpha}{2}\mathbf w^T \mathbf w\right)
\end{eqnarray}
となります.ハイパーパラメータ$\alpha$はガウス分布の精度を表すスカラーです.また,尤度は出力$y_i=f(x_i;\mathbf w)+\epsilon_i$から次のようになります.
\begin{eqnarray}
p(\mathbf y|\mathbf x,\mathbf w,\beta)
&=&\prod_{i=1}^{N} \sqrt \frac{\beta}{2\pi}\exp\left(-\frac{\beta}{2}\left(y_i-\mathbf w^T\boldsymbol \phi(x_i)\right)^2\right)
\end{eqnarray}
これら尤度と事前分布から,データセットに対する事後分布はベイズの定理より
$$p(\mathbf w|\mathbf x,\mathbf y,\alpha,\beta)=\frac{p(\mathbf y|\mathbf x,\mathbf w,\beta)p(\mathbf w|\alpha)}{p(\mathbf y|\mathbf x, \alpha,\beta)}$$
となって,更に事後分布に対数を取ると次のようになります.
\begin{eqnarray}
\ln p\left(\mathbf w|\mathbf x,\mathbf y, \alpha, \beta\right)
&=& \ln p\left(\mathbf y|\mathbf x, \mathbf w, \beta\right)+\ln p\left(\mathbf w|\alpha\right) - \ln p\left(\mathbf y|\mathbf x,\alpha,\beta\right)\\
&=&\ln \left(\prod_{i=1}^{N} N(y_i|\mathbf w^T\boldsymbol \phi(x_i),\beta^{-1})\right)+\ln N(\mathbf{w}|\mathbf 0,\alpha^{-1}\mathbf I) + const\\
&=&\ln \left(\prod_{i=1}^{N} \sqrt \frac{\beta}{2\pi}\exp\left(-\frac{\beta}{2}\left(y_i-\mathbf w^T\boldsymbol \phi(x_i)\right)^2\right)\right)+\ln \left(\left(\frac{\alpha}{2\pi}\right)^{\frac{D}{2}}\exp\left(-\frac{\alpha}{2}\mathbf w^T \mathbf w\right)\right) + const\\
&=&\sum_{i=1}^N\left(\frac{1}{2}\ln \frac{\beta}{2\pi}-\frac{\beta}{2}\left(y_i-\mathbf w^T\boldsymbol \phi(x_i)\right)^2\right)+\left(\frac{D}{2}\ln\frac{\alpha}{2\pi}-\frac{\alpha}{2}\mathbf w^T\mathbf w\right)+const\\
&=&-\frac{\beta}{2}\sum_{i=1}^{N}\left(y_i-\mathbf w^T\boldsymbol \phi(x_i)\right)^2-\frac{\alpha}{2}\mathbf w^T\mathbf w+\frac{N}{2}\ln \frac{\beta}{2\pi}+\frac{D}{2}\ln \frac{\alpha}{2\pi}+const\\
&=&-\frac{\beta}{2}\sum_{i=1}^{N}\left(y_i-\mathbf w^T\boldsymbol \phi(x_i)\right)^2-\frac{\alpha}{2}\mathbf w^T\mathbf w+const\\
&=&-\frac{\beta}{2}\|\mathbf{y}-\Phi\mathbf{w}\|^{2}-\frac{\alpha}{2}\|\mathbf{w}\|^{2} + const
\end{eqnarray}
ここで,1行目の右辺の周辺尤度$p(\mathbf y|\mathbf x,\alpha,\beta)$と5行目の第3項と第4項は,パラメータ$\mathbf{w}$に対して定数であるため$const$にまとめています.また,対数事後分布$\ln p(\mathbf{w}|\mathbf x,\mathbf y, \alpha, \beta)$をパラメータ$\mathbf{w}$の目的関数$M(\mathbf{w})$とみなすと次のようになります.
\begin{eqnarray}
M(\mathbf{w})
&=&-\frac{\beta}{2}\|\mathbf{y}-\Phi\mathbf{w}\|^{2}-\frac{\alpha}{2}\|\mathbf{w}\|^{2} + const
\end{eqnarray}
ここで,Ridge回帰(制約付き二乗誤差)の目的関数$E(\mathbf w)$は
\begin{eqnarray}
E(\mathbf{w})=\frac{1}{2}\|\mathbf{y}-\Phi\mathbf{w}\|^{2}+\frac{\lambda}{2}\|\mathbf{w}\|^{2}
\end{eqnarray}
となり,$M(\mathbf{w})$を$\beta$で割って$\lambda=\frac{\alpha}{\beta}$とすると,$M(\mathbf{w})$の最大化と$E(\mathbf{w})$の最小化は同じになります.従って,ノイズ$\epsilon$と事前分布$p(\mathbf w|\alpha)$がガウス分布のとき,MAP推定とRidge回帰(制約付き二乗誤差)の結果は等価になることが分かります.
1-2 目的関数を偏微分して,極値を求める
事後分布が最大になるパラメータ$\mathbf{w}_{MAP}$は,目的関数$M(\mathbf{w})$が2次形式で上に凸形状なので,$\mathbf{w}$で偏微分して0になる極値から求められます.
\begin{eqnarray}
\frac{\partial M(\mathbf{w})}{\partial \mathbf{w}}
&=&\frac{\partial}{\partial \mathbf{w}}\{-\frac{\beta}{2}(\mathbf{y}-\Phi\mathbf w)^{T}(\mathbf{y}-\Phi\mathbf{w})-\frac{\alpha}{2}\mathbf w^T\mathbf w+const\}\\
&=&\frac{\partial}{\partial \mathbf{w}}\{-\frac{\beta}{2}(\mathbf{y}^T\mathbf{y}-\mathbf{y}^T\Phi\mathbf{w}-\mathbf{w}^T\Phi^T\mathbf{y}+\mathbf{w}^T\Phi^T\Phi\mathbf{w})-\frac{\alpha}{2}\mathbf w^T\mathbf w+const\}\\
&=&\frac{\partial}{\partial \mathbf{w}}\{-\frac{\beta}{2}(\mathbf{y}^T\mathbf{y}-2\mathbf{w}^T\Phi^T\mathbf{y}+\mathbf{w}^T\Phi^T\Phi\mathbf{w})-\frac{\alpha}{2}\mathbf w^T\mathbf w+const\}\\
&=&-\frac{\beta}{2}(0-2\Phi^T\mathbf{y}+2\Phi^T\Phi\mathbf{w})-\alpha\mathbf{w}+0\}\\
&=&\beta\Phi^T\mathbf{y}-\beta\Phi^T\Phi\mathbf{w}-\alpha\mathbf{w}\\
&=&0
\end{eqnarray}
次に,両辺を$\beta$で割って式変形をすると次の式になります($\lambda=\frac{\alpha}{\beta}$としています).
\begin{eqnarray}
(\Phi^{T}\Phi\mathbf+\lambda I)\mathbf{w}&=&\Phi^{T}\mathbf{y}\\
\end{eqnarray}
従って,MAP推定で求められた$\mathbf{w}_{MAP}$は,
\begin{eqnarray}
\mathbf{w}_{MAP}
=(\Phi^{T}\Phi+\lambda I)^{-1}\Phi^T\mathbf{y}
\end{eqnarray}
となります.
2. 推定したパラメータから,新規入力に対する出力を予測する
推定した$\mathbf{w}_{MAP}$を用いると新規入力$x^*$に対する出力$y^*$は次の式になります.
\begin{eqnarray}
y^{*}\simeq f(x^{*})=\mathbf{w}_{MAP}^{T}\boldsymbol{\phi}(x^*)
\end{eqnarray}
MAP推定を用いた回帰の実装
導出した式を使い,スクラッチで実装しました.
MAP推定を用いた回帰の実装
# MAP推定
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
def Phi(X):
# X : [[x0],[x1],...]
# phi : e.g. [1, x, x**2]
# return : [[phi_1(X),...,phi_n(X)]]
result = np.array([[1, x[0], x[0]**2, x[0]**3, x[0]**4, x[0]**5, x[0]**6, x[0]**7, x[0]**8, x[0]**9] for x in X])
return result
N = 10
alpha = 0.003 # ハイパーパラメータ
beta = 0.3 # 既知と仮定しています
np.random.seed(1111)
x = np.linspace(-1,1,N)
t = np.sin(np.pi*np.linspace(-1.5,1.5,100))
y = np.sin(np.pi*x) + np.random.normal(0,beta,N)
x_test = np.linspace(-1.5,1.5,100)
y_test = np.sin(np.pi*x_test) + np.random.normal(0,beta,len(x_test))
# 縦ベクトルに変換
x = np.array([[i] for i in x])
x_test = np.array([[i] for i in x_test])
# MAP推定はここが変化するだけ
w_MAP = np.dot(np.dot(np.linalg.inv(np.dot(Phi(x).T, Phi(x))+(alpha/beta)*np.eye(10)), Phi(x).T), y)
w_MAP = np.array([[w] for w in w_MAP])
predict = np.dot(w_MAP.T, Phi(x_test).T).ravel()
fig, ax = plt.subplots(1,2,figsize=(12,4))
ax[0].plot(np.linspace(-1.5,1.5,len(t)),t,label='sin',color='b')
ax[0].plot(x_test.ravel(), predict.ravel(),label='predict curve',color='r')
ax[0].scatter(x.ravel(), y, label='train_data',color='b')
ax[1].plot(x_test.ravel(), predict.ravel(),label='predict curve',color='r')
ax[1].scatter(x_test.ravel()[::5],y_test[::5], label='test_data',color='0.1')
ax[0].set_title('train')
ax[1].set_title('test')
ax[0].set_xlim(-1.5,1.5)
ax[0].set_ylim(-1.5,1.5)
ax[1].set_xlim(-1.5,1.5)
ax[1].set_ylim(-1.5,1.5)
ax[0].legend(loc='upper right',fontsize=9)
ax[1].legend(loc='upper right',fontsize=9)
plt.show()
for i, w in enumerate(w_MAP.ravel()):
print('w{}: {:.3f}'.format(i,w),end=' ')
実験結果
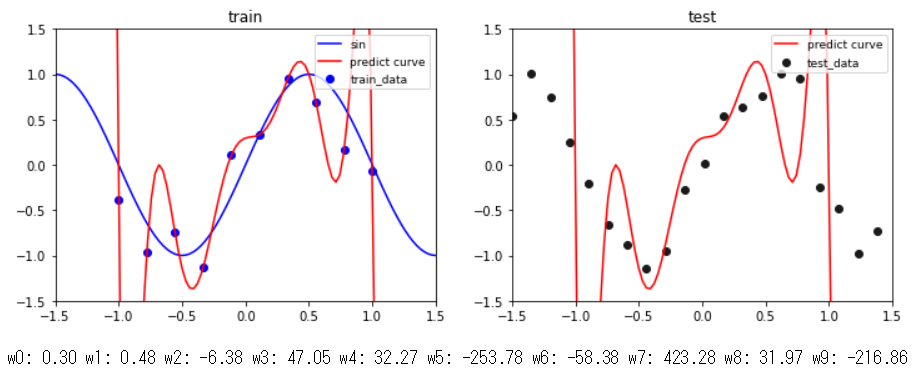
最尤推定(第1回目)の実験で使用したデータセットと同じものを使って,$\alpha=0$(分散無限大),$\beta=0.3$(既知)で9次多項式のパラメータ$\mathbf{w}$をMAP推定したのがこの結果です.$\mathbf{w}$への制約が働いていないため過学習していることが,曲線が学習データ全てを通っていることや$\mathbf w$が極端に大きな値になっていることから分かります.また,この結果は最尤推定の9次多項式の結果と全く同じになっていることが分かります.
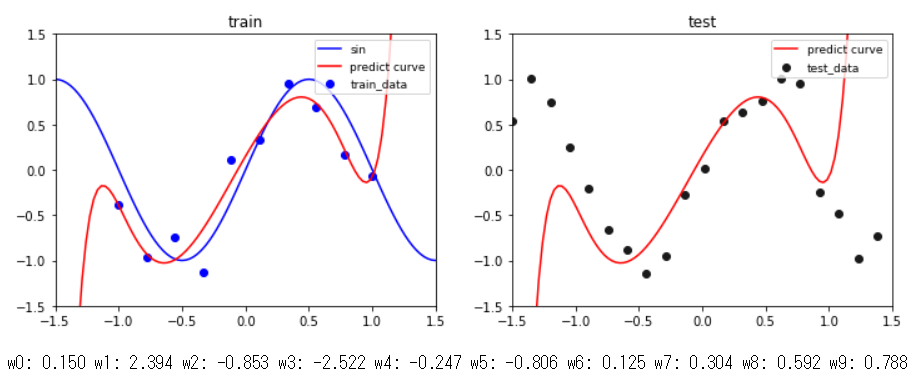
同じ条件で,$\alpha=0.03$に変更したのがこの結果です.学習データ,テストデータともに$x$が-1から1の範囲内でデータに上手く曲線フィッテングできることが分かります(一方で,$x$が-1から1の範囲外については学習していないので上手くできていません).更に,事前分布によって表現力が制約され,パラメータ$\mathbf w$があまり大きな値を取れていないことが分かります.
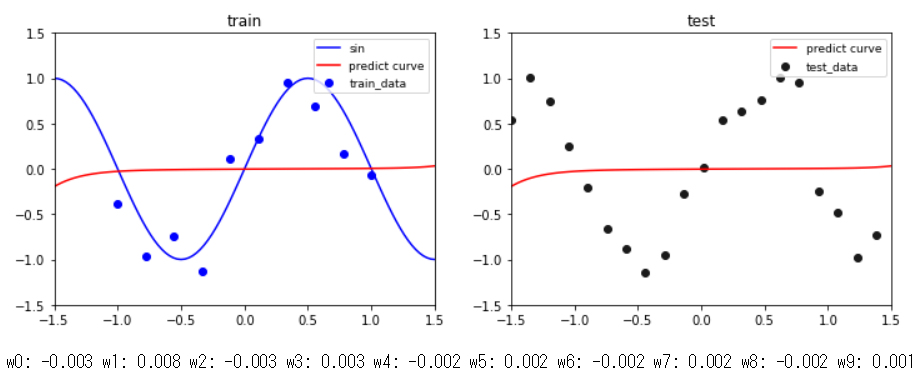
同じ条件で,$\alpha=100$(分散小さめ)にしたのがこの結果です.事前分布の制約が強すぎるため,上手く学習データを通るような曲線が引けていないことが分かります.また,パラメータ$\mathbf{w}$の値を見ると,全て0付近の値になっていることが分かります.
まとめ
数式の導出から,MAP推定を使った回帰がRidge回帰と等価になることを示しました.更に,実験から事前分布(正則化)のハイパーパラメータ$\alpha$を調整することでモデルの表現能力を制約し,モデルを変えずに適切な回帰ができることを確認しました.