この記事は古川研究室 Workout_calendar 12日目の記事です.
本記事は古川研究室の学生が学習の一環として書いたものです.内容が曖昧であったり表現が多少異なったりする場合があります.
概要
はじめに,私は今回のイベントで3本記事を出します.一貫して回帰がテーマになっていますが,それぞれ違うパラメータ推定方法でアプローチしているのが特徴です.具体的に,第1回では最尤推定,第2回ではMAP推定,第3回ではベイズ推定を用いて回帰を行います.もし,興味があれば本記事だけでなく第2回や第3回も見て頂けると嬉しいです.
本記事の内容をざっくり言うと,最尤推定を使用して回帰モデルのパラメータ$\mathbf w,\beta$を推定し,新規入力に対する出力の予測分布を求めたり,最尤推定で得られる結果が最小二乗法と等価になっていることを確認します.
この記事で行ったことをリスト化すると以下のようになっています.
「記事内で行ったこと」
- (理論)最尤推定を用いたモデルのパラメータと予測分布の導出
- (実装)最尤推定を用いた回帰のスクラッチ実装
まずは,簡単に用語などの説明を行いたいと思います
最尤推定,MAP推定,ベイズ推定について
データセット$X$が与えられている状況で,モデルのパラメータ$\mathbf{w}$を推定する統計的な手法に最尤推定,MAP推定,ベイズ推定があります.これらの手法は,最尤推定とMAP推定がモデルのパラメータ$\mathbf{w}$に関して,最も「良い」答えをただ一つ求める点推定(それ以外の他の可能性は全て切り捨てる)なのに対して,ベイズ推定はパラメータ$\mathbf{w}$に関して「良い」だけでなく,「まあまあ良い」答えなどあらゆる答え(可能性)を含んだ分布を推定できることが大きな違いです.ここで,ベイズの定理は次のような式になっています.
\begin{eqnarray}
p(\mathbf{w}|X)=\frac{p(X|\mathbf{w})p(\mathbf{w})}{p(X)}
\end{eqnarray}
以下は,この定理を使ったパラメータ推定方法です.
①最尤推定(事前知識なしで尤度$p(X|\mathbf{w})$を最大にするパラメータを選ぶ)
\begin{eqnarray}
\mathbf{w}_{ML}=\underset{w}{\arg \max \,}p(X|\mathbf{w})
\end{eqnarray}
②MAP推定(事前知識ありで事後分布$p(\mathbf{w}|X)$を最大にするパラメータを選ぶ)
\begin{eqnarray}
\mathbf{w}_{MAP}=\underset{w}{\arg \max \,}p(X|\mathbf{w})p(\mathbf{w})
\end{eqnarray}
③ベイズ推定(パラメータ$\mathbf{w}$の分布を推定する)
\begin{eqnarray}
p(\mathbf{w}|X)=\frac{p(X|\mathbf{w})p(\mathbf{w})}{p(X)}
\end{eqnarray}
尤度とは
本記事では,データセット$X$が与えられているとき,ベイズの定理から次の式が得られます.
\begin{eqnarray}
p(\mathbf{w}|X,\beta)=\frac{p(X|\mathbf{w},\beta)p(\mathbf{w})}{p(X)}
\end{eqnarray}
$\mathbf w$と$\mathbf \beta$はそれぞれパラメータです(詳細は後で出てきます).このとき,$p(X|\mathbf w,\beta)$を尤度,$p(\mathbf w)$を事前分布,$p(X)$をエビデンス,$p(\mathbf w|X,\beta)$を事後分布といいます.ここで,$X$は与えられているので確率変数ではなく,$\mathbf w,\beta$は確率変数です.
尤度$p(X|\mathbf w,\beta)$は,既に手に入ったデータセット$X$からパラメータ$\mathbf w,\beta$を見て,$\mathbf w,\beta$が何か一意に決まったときの$X$に対する尤もらしさを表します.ここで,尤度は分布全てを足しても1にはならないため,確率ではありません.そのため尤度は,尤度関数とも呼ばれます.
もし文章で分からなければこちらの記事をご覧ください.視覚的に説明されていて,文章でイメージするよりも分かりやすいのでとてもおすすめです.
最尤推定による回帰のタスク設定
与えられているもの
入力$\mathbf x=(x_1,...,x_N), x\in\mathbf R$と出力$\mathbf y=(y_1,...,y_N), y\in\mathbf R$のデータセット
仮定
・$\mathbf x$と$\mathbf y$のデータセットは,独立同分布(i.i.d.)に従うとします.
・$y_i,f,\epsilon$を次のように仮定します($\beta$はガウスノイズの精度です).
\begin{eqnarray}
y_i&=&f(x_i;\mathbf w)+\epsilon_i
\end{eqnarray}
\begin{eqnarray}
f(x_i;\mathbf w)=\mathbf{w}^T\boldsymbol{\phi}(x_i)
\end{eqnarray}
\begin{eqnarray}
\epsilon_i&\sim& N(0,\beta^{-1})
\end{eqnarray}
$;;;$ここで,基底関数$\boldsymbol{\phi}(x)$とパラメータ$\mathbf{w}$は$D$個あるので次のようになります.
\begin{eqnarray}
\boldsymbol{\phi}(x_i)&=&(\phi_1(x_i),...,\phi_{D}(x_i))^T
\end{eqnarray}
\begin{eqnarray}
\mathbf{w}&=&(w_1,...,w_{D})^T
\end{eqnarray}
最尤推定のタスク
尤度が最大となるパラメータ$\mathbf w_{ML},\beta_{ML}$を推定します.
\begin{eqnarray}
\mathbf w_{ML},\;\beta_{ML}
&=&\underset{\mathbf{w},\;\beta}{\arg \max\;}p(\mathbf y|\mathbf x,\mathbf{w},\beta)\\\
&=&\underset{\mathbf{w},\;\beta}{\arg \max\,}\prod_{i=1}^{N}p(y_i|x_i,\mathbf{w},\beta)\
\end{eqnarray}
推定した$\mathbf w_{ML},\beta_{ML}$から,新規入力$x^*$に対する出力$y^{*}$の予測分布$p(y^*|x^*,\mathbf
w_{ML},\beta_{ML})$を求めることができます.
解析解の導出
-
対数尤度関数を最大化するパラメータ$\mathbf w_{ML},\mathbf{\beta}_{ML}$を求める
1-1 尤度の式を変形して対数尤度関数を求める
1-2 対数尤度関数を偏微分して,極値を求める -
推定したパラメータ$\mathbf w_{ML},\mathbf \beta_{ML}$から,新規入力$x^*$に対する出力$y^*$の予測分布を求める
1. 対数尤度関数を最大化するパラメータを求める
1-1 尤度の式を変形して対数尤度関数を求める
はじめに,観測データが$(x_i,y_i)$,出力が$y_i=f(x_i;\mathbf w)+\epsilon_i$とすると,尤度$p\left(y_i|x_i,\mathbf w,\beta\right)$を次のように仮定します.
\begin{eqnarray}
p\left(y_i|x_i,\mathbf{w},\beta\right)
&=&N\left(y_i|f(x_i;\mathbf w),\beta^{^-1}\right)\\
&=&\sqrt\frac{\beta}{{2\pi}}\exp\left(-\frac{\beta}{2}(y_i-f(x_i;\mathbf w))^{2}\right)\\
&=&\sqrt\frac{\beta}{{2\pi}}\exp\left(-\frac{\beta}{2}\left(y_i-\mathbf{w}^{T}\boldsymbol{\phi}\left(x_i\right)\right)^{2}\right)
\end{eqnarray}
次に,データセット全体の尤度を求めると,独立同分布(i.i.d.)に従うと仮定しているので次のようになります.
\begin{eqnarray}
\prod_{i=1}^{N} p\left(y_i|x_i,\mathbf{w},\beta\right)=p(y_1|x_1,\mathbf{w},\beta)\times \cdots \times p(y_N|x_N,\mathbf{w},\beta)
\end{eqnarray}
更に,対数尤度は次のように求められます.
\begin{eqnarray}
\ln \left(\prod_{i=1}^{N} p\left(y_i|x_i,\mathbf{w},\beta\right)\right)
&=&\sum_{i=1}^{N}\ln p(y_i|x_i,\mathbf{w},\beta)\\
&=&\sum_{i=1}^{N} \{ \frac{1}{2}\ln \frac{\beta}{2\pi}-\frac{\beta}{2}(y_i-\mathbf{w}^{T}\boldsymbol{\phi}(x_i))^{2} \} \\
&=&-\frac{\beta}{2}\sum_{i=1}^{N}(y_i-\mathbf{w}^{T}\boldsymbol{\phi}(x_i))^{2}+\frac{N}{2}\ln \beta-\frac{N}{2}\ln {2\pi}\\
&=&-\frac{\beta}{2}\|\mathbf{y}-\Phi\mathbf{w}\|^{2}+\frac{N}{2}\ln \beta-\frac{N}{2}\ln {2\pi}
\end{eqnarray}
ここで,$N$,$D$はデータ数と基底関数の数を表しており,$\mathbf{y},\mathbf{w},\Phi$はそれぞれ次のようになっています.
\begin{eqnarray}
\mathbf{y}&=&\left(y_1,...,y_N\right)^{T}\\
\mathbf{w}&=&(w_1,...,w_D)^{T}\\
\Phi &=&
\left(
\begin{array}{cccc}
\phi_{1}(x_1) & \cdots & \phi_{D}(x_1)\\
\vdots & \ddots & \vdots\\
\phi_{1}(x_N) & \cdots & \phi_{D}(x_N)\\
\end{array}
\right)\\
\end{eqnarray}
求めた対数尤度はパラメータ$\mathbf{w},\beta$による関数とみなせるので,対数尤度関数$L(\mathbf{w},\beta)$とおくと次のようになります.
\begin{eqnarray}
L(\mathbf{w},\beta)&=&-\frac{\beta}{2}\|\mathbf{y}-\Phi\mathbf{w}\|^{2}+\frac{N}{2}\ln \beta-\frac{N}{2}\ln {2\pi}\\
&=&-\beta\frac{1}{2}\|\mathbf{y}-\Phi\mathbf{w}\|^{2}+\frac{N}{2}\ln \beta-\frac{N}{2}\ln {2\pi}\\
&=&-\beta E(\mathbf{w})+\frac{N}{2}\ln \beta-\frac{N}{2}\ln {2\pi}
\end{eqnarray}
ここで,$E(\mathbf{w})=\frac{1}{2}\|\mathbf{y}-\Phi\mathbf{w}\|^{2}$です.
この式のパラメータ$\mathbf{w}$について注目すると,第二項と第三項は定数であり,第一項は$\beta$(スカラー)倍された目的変数とモデルの出力の二乗誤差$E(\mathbf{w})$になっていることが分かります.つまり,パラメータ$\mathbf{w}$に関して尤度関数を最大化するということは二乗誤差を最小にするという問題と等価であることを示しています.このことから,回帰における最小二乗法を解くという行為は最尤推定という統計的手法によって妥当性が裏付けられた解き方であるということが分かります.ただし,ガウスノイズの仮定の下でのみ成り立つことに注意しなければいけません.
1-2 対数尤度関数を偏微分して,極値を求める
① $\mathbf{w}$で偏微分して,極値を求める
次に,先ほど導出した対数尤度関数$L(\mathbf{w},\beta)$を$\mathbf{w}$で偏微分し,$0$となる極値$\mathbf{w}_{ML}$を求めます.ここで,パラメータ$\mathbf{w}$に関係ないとみなせる定数項は全て$const$にまとめています.
\begin{eqnarray}
\frac{\partial L(\mathbf{w},\beta)}{\partial \mathbf{w}}
&=&\frac{\partial}{\partial \mathbf{w}}\{-\frac{\beta}{2}\|\mathbf{y}-\Phi\mathbf{w}\|^{2}+const\}\\
&=&\frac{\partial}{\partial \mathbf{w}}\{-\frac{\beta}{2}(\mathbf{y}-\Phi\mathbf{w})^{T}(\mathbf{y}-\Phi\mathbf{w})+const\}\\
&=&\frac{\partial}{\partial \mathbf{w}}\left\{-\frac{\beta}{2}\left(\mathbf{y}^T\mathbf{y}-\mathbf{y}^T\Phi\mathbf{w}-\mathbf{w}^T\Phi^T\mathbf{y}+\mathbf{w}^T\Phi^T\Phi\mathbf{w}\right)+const\right\}\\
&=&\frac{\partial}{\partial \mathbf{w}}\left\{-\frac{\beta}{2}\left(\mathbf{y}^T\mathbf{y}-\mathbf{w}^T(\mathbf{y}^T\Phi)^T-\mathbf{w}^T\Phi^T\mathbf{y}+\mathbf{w}^T\Phi^T\Phi\mathbf{w}\right)+const\right\}\\
&=&\frac{\partial}{\partial \mathbf{w}}\left\{-\frac{\beta}{2}\left(\mathbf{y}^T\mathbf{y}-2\mathbf{w}^T\Phi^T\mathbf{y}+\mathbf{w}^T\Phi^T\Phi\mathbf{w}\right)+const\right\}\\
&=&-\frac{\beta}{2}(0-2\Phi^T\mathbf{y}+2\Phi^T\Phi\mathbf{w})+0\\
&=&0
\end{eqnarray}
ここで,上から3行目第2項に出てくる$\mathbf{y}^T\Phi\mathbf{w}$は,$\mathbf{a},\mathbf{b}$がベクトルの時に成り立つ$\mathbf{a}^T\mathbf{b}=\mathbf{b}^T\mathbf{a}$の関係を利用して,$\mathbf{a}^T=\mathbf{y}^T\Phi$,$\mathbf{b}=\mathbf{w}$と置いて式変形を行いました.
従って,式を整理すると次の式が得られます.
\begin{eqnarray}
\Phi^{T}\Phi\mathbf{w}=\Phi^{T}\mathbf{y}
\end{eqnarray}
よって,最尤推定で求められた$\mathbf{w}_{ML}$は,
\begin{eqnarray}
\mathbf{w}_{ML}
&=&(\Phi^{T}\Phi)^{-1}\Phi^T\mathbf{y}\\
&=&\Phi^{\dagger}\mathbf{y}
\end{eqnarray}
となります.この式は,最小二乗法の正規方程式として知られています.また,$N×D$行列$\Phi^{\dagger}$はムーア=ペンローズの一般化逆行列もしくは疑似逆行列と呼ばれ,長方行列に対しての逆行列みたいなものと考えることができます.余談ですが,もし仮に$N=D$で$\Phi$が正則であるとすると,$(AB)^{-1}=B^{-1}A^{-1}$より,
\begin{eqnarray}
\Phi^{\dagger}
&=&(\Phi^{T}\Phi)^{-1}\Phi^T\\
&=&\Phi^{-1}(\Phi^T)^{-1}\Phi^T\\
&=&\Phi^{-1}
\end{eqnarray}
となって,$\Phi^{\dagger}=\Phi^{-1}$が成り立つことが分かります.
② $\beta$で偏微分して,極値を求める
次に,$\beta_{ML}$を求めます.ここで,対数尤度関数$L(\mathbf{w},\beta)$は以下の式となっており,
\begin{eqnarray}
L(\mathbf{w},\beta)
=-\frac{\beta}{2}\|\mathbf{y}-\Phi\mathbf{w}\|^{2}+\frac{N}{2}\ln \beta-\frac{N}{2}\ln {2\pi}
\end{eqnarray}
この式を$\beta$について偏微分し,$0$となる極値を求めます.
\begin{eqnarray}
\frac{\partial L\left(\mathbf{w},\beta\right)}{\partial \beta}
&=&-\frac{1}{2}\|\mathbf{y}-\Phi\mathbf{w}\|^{2}+\frac{N}{2\beta_{ML}}+0
&=&0
\end{eqnarray}
得られた式を$\beta_{ML}$について整理すると次のようになります.
\begin{eqnarray}
\frac{1}{\beta_{ML}}
=\frac{1}{N}\sum_{i=1}^{N}(y_i-\mathbf{w}^{T}\boldsymbol{\phi}(x_i))^{2}
\end{eqnarray}
この式は,最尤推定で求めたガウスノイズの分散($\beta_{ML}^{-1}$)は平均二乗誤差の値と等しくなるということを示しています.
2. 推定したパラメータから,新規入力に対する出力の予測分布を求める
推定した$\mathbf w_{ML},\beta_{ML}$から,予測分布$p(y^{*}|x^{*},\mathbf w_{ML},\beta_{ML})$は次のようになります.
\begin{eqnarray}
p(y^{*}|x^{*},\mathbf{w}_{ML},\beta_{ML})
&=&N\left(y^{*}|f(x^{*};\mathbf w_{ML}),\beta_{ML}^{-1}\right)\\
&=&N\left(y^{*}|\mathbf{w}_{ML}^{T}\boldsymbol{\phi}(x^{*}),\beta_{ML}^{-1}\right)
\end{eqnarray}
最尤推定を用いた回帰の実装
導出した式から,スクラッチで実装を行いました
# 最尤推定
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
np.set_printoptions(precision=3)
def Phi(X):
# X : [[x0],[x1],...]
# phi : e.g. [1, x, x**2]
# return : [[phi_1(X),...,phi_n(X)]]
result = np.array([[1, x[0], x[0]**2, x[0]**3] for x in X])
return result
N = 10
beta = 0.3
np.random.seed(1111)
x = np.linspace(-1,1,N)
t = np.sin(np.pi*np.linspace(-1.5,1.5,100))
y = np.sin(np.pi*x) + np.random.normal(0,beta,N)
x_test = np.linspace(-1.5,1.5,100)
y_test = np.sin(np.pi*x_test) + np.random.normal(0,beta,len(x_test))
# 学習
x = np.array([[i] for i in x])
x_test = np.array([[i] for i in x_test])
y = np.array([[i] for i in y])
w_ML = np.dot(np.dot(np.linalg.inv(np.dot(Phi(x).T, Phi(x))), Phi(x).T), y.ravel())
w_ML = np.array([[w] for w in w_ML])
# テスト
predict = np.dot(w_ML.T, Phi(x_test).T).ravel()
variance_ML = np.sum(np.square(y-np.dot(Phi(x), w_ML))) / N
sigma = np.sqrt(variance_ML)
fig, ax = plt.subplots(1,2,figsize=(12,4))
ax[0].plot(np.linspace(-1.5,1.5,len(t)),t,label='sin',color='b')
ax[0].plot(x_test.ravel(), predict.ravel(),label='predict curve',color='r')
ax[0].scatter(x.ravel(), y, label='train_data',color='b')
ax[1].fill_between(x_test.ravel(), predict+sigma*3, predict-sigma*3, alpha=0.1, label='3sigma')
ax[1].fill_between(x_test.ravel(), predict+sigma, predict-sigma, alpha=0.1, label='sigma')
ax[1].plot(x_test.ravel(), predict.ravel(),label='predict curve',color='r')
ax[1].scatter(x_test.ravel()[::5],y_test[::5], label='test_data',color='0.1')
ax[0].set_title('train')
ax[1].set_title('test')
ax[0].set_xlim(-1.5,1.5)
ax[0].set_ylim(-1.5,1.5)
ax[1].set_xlim(-1.5,1.5)
ax[1].set_ylim(-1.5,1.5)
ax[0].legend(loc='upper right',fontsize=9)
ax[1].legend(loc='upper right',fontsize=9)
plt.show()
for i, w in enumerate(w_ML.ravel()):
print('w{}: {:.2f}'.format(i,w),end=' ')
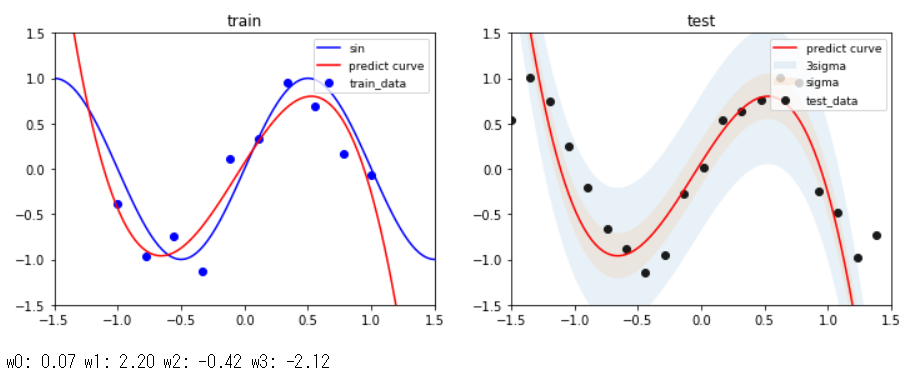
実験結果 3次多項式のとき
sin関数からサンプリングした10点の学習データに対して,3次多項式のモデルを使って回帰を行った結果がこれです.$x$の定義域が-1.5から1.5付近までは,学習データもテストデータもある程度上手くできてることが分かります.また,パラメータ$\mathbf{w}$は,あまり大きな値になっていない(過学習していない)ことが分かります.分散(sigma)については,ある程度広がりを持っていることが右図から分かります.
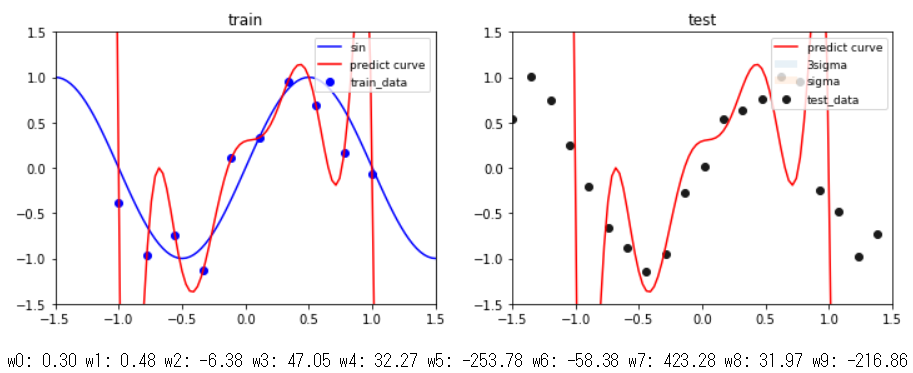
実験結果 9次多項式のとき
同じ条件で,9次多項式のモデルで回帰を行った結果がこれです.左図を見ると全ての学習データを通る曲線になっていることが分かりますが,一方で右図のテストデータには全然上手くいっていないことが分かります.パラメータ$\mathbf{w}$の値を見てみると3次多項式の結果と比べてかなり大きな値になっていることが分かり,このことから学習データに対して過学習していると考えられます.また,全ての学習データを通る曲線になっているので平均二乗誤差が$0$となり,分散(sigma)がないことが右図から分かります.
感想
数式の導出とスクラッチによる実装を行ったことで,最尤推定を使った回帰のイメージがつかめたと思います.