アルゴリズムで実社会を捉える～評価関数の作り方～

フューチャー Advent Calendar 2019の21日目¹の記事です。

普段は会社のAIチームで特定のAI分野に属さない問題や、最適化問題を担当しています。
本記事では、競技プログラミングにおける所謂ゲームAI系のコンテストを起点に、評価関数を作成する際に私が意識していることを紹介します。
そこから波及して、実社会の問題をアルゴリズムで解く際に、人間の感覚を如何に評価関数に落とせばよいのかについて言及します。

良し悪しを量ったことのないあなたへ

　本記事は、ゲームAIコンテスト²を主とした、計算量爆発により最善手は求められない問題に取り組んだ経験がないという人に向けた記事です。学術的に体系立てられるようなものではありませんが、コンテストや実業務を通じて得た実践的な知見をお伝えできればと思います。
　「ゲームAIコンテスト…とは？」という方は、過去記事を一読頂けると雰囲気がわかるかと思います。

• 競技プログラミングにおけるゲーム木探索の面白さ

　なお、この記事では評価関数の項目や重みを人の手で作ることを前提としています。また、評価関数の作成では実社会の最適化問題における目的関数のそれと近しい部分があり、対戦形式にてより柔軟で破綻しにくい評価関数を作ることと、実社会の最適化問題における目的関数を作ることを同一視します。それでは、一緒に世界を推し量りましょう。

評価関数とは

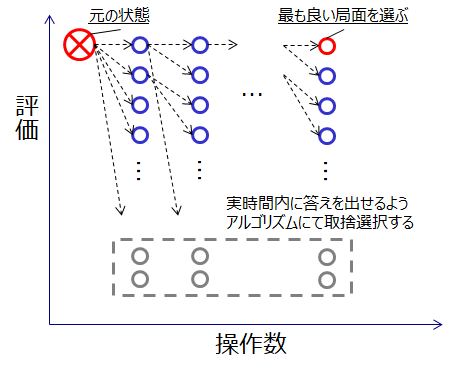
　ゲームAI系コンテストでは、主に2人以上での対戦ゲームで勝ち負けを競います。将棋や囲碁、リバーシ、ぷよぷよ、ボンバーマン等をイメージ頂くと良いです。それらのゲームを人間がコントローラーを操作する代わりに、プログラムによって回答を出力することで操作するのがゲームAI系コンテストです。その操作パターンは膨大なものとなり、限られた時間内に全てを調べることはできません。そこで、あるゲームの局面に対して評価を付け、その評価がなるべく高くなる操作を選ぶことで、実時間内に回答を提出しようというアプローチを取ります。その評価を付ける関数を評価関数と呼びます。
　もし仮に、完璧な評価関数が作れたとしたら、次の操作で勝てる手(負けにくい手)を選び続けるだけで勝て(負けず)、線形時間の処理で済みます。しかし、実際の評価関数は完全ではなく、ある局面のみを見た場合にその評価にズレがあることが多いです。そのため、探索木³と組合せて先読みをすることで、致命的なズレを回避し、最善の操作を決定します。

目的関数とは

　最適化問題(1人ゲーム問題とみなせる)において、ある関数の戻り値を最大化・或いは最小化すべきものとして定義されるものを目的関数と言います。例えば、巡回セールスマン問題における移動距離や、ナップサック問題におけるナップサックに入れられた品物の価値がそれに当たります。
　ある最適化問題が提示された際、目的関数は既に厳密に定義されています。しかし、実社会の数々の問題は明確に線引できない要素や、誤差なく計測できない項目によって成り立っており⁴、数理最適の問題にはめ込む際には何らかの単純化・モデル化を行い目的関数を決定します。その際の考え方は評価関数の導出に通じるものがあると考えており、記事中で折を見て触れます。

評価関数の作り方

　具体例としてリバーシを取り上げます。リバーシでは最終的に石の数で勝敗が決まります。このことから、石の数を評価関数に加えるのは自然な発想です。しかし、ゲームの序盤中盤では単純な石の数ではなく、四隅を取ることが非常に重要です。逆に、相手に四隅を取られることを避けなければならないため、四隅の周囲に置くことは避けるべきです。このように、ゲームの最終的なスコアが単純でも、その結果に辿り着くまでの途中局面は様々な評価観点があり、それらを適切に組み合わせ、観点毎の重みのバランスを調整する必要があります。

// 単純な評価関数
評価 = 自石 - 敵石

// 少し工夫した評価関数
評価 = (自石 - 敵石) + α * (四隅の自石 - 四隅の敵石) - β * (未置四隅の自石 - 未置四隅の敵石)

　このような評価関数のデザインはあまりに自由度が高い一方、書籍やチュートリアルで紹介されるのはおもちゃレベルのものに留まっており、一種の職人芸の様相を呈しています。強いゲームAIとなる評価関数を開発者のセンスに頼り切らずに作れるよう、私は大きく3つの指針を持って取り組んでいます。

• 基準となる観点を定める
• 静止状態で評価する
• トレードオフの関係に注意する

基準となる観点を定める

　評価関数の各要素のバランスを考える際に拠り所になる基準が無いと、パラメータ調整に多大なコストを払うことになり、上手くバランスが取れないとめちゃくちゃな動きをするAIとなります。それを避けるため、主にゲームの根幹となる要素を基準とすることを推奨します。
　例えばリバーシであれば、やはり石の数を基準にするのが良いでしょう。石ひとつ対する点数を1点とした場合、四隅の石は最終的に石の獲得にどの程度貢献するかを考えることができます。仮に、四隅のひとつが取れれば縦横斜めの 7 × 3 = 21石 程度の取得に貢献するとみなし、通常の21点を与えるというような考え方があります。また、未置四隅に置いてしまうと相手に21点を取られてしまう可能性があるため、約半分の-10点を与えるという考え方もあります。

// 観点を定めた評価関数
評価 = (自石 - 敵石)
       + 21 * (四隅の自石 - 四隅の敵石)
       - 10 * (未置四隅の周囲の自石 - 未置四隅の周囲の敵石)

　上記は整数値(int)の例でしたが、実数値(double)で持つことや、高速化のために整数値(int)型で値を持つために石ひとつを100点/1,000点等にし、石ひとつより細かな差異を表現するテクニックがあります。

　実社会、特にビジネス活動ではお金を基準にするとほぼ間違いないです。例えば、巡回セールスマン問題では、移動距離自体ではなく移動にかかるお金(人件費 + 交通費(電車/タクシー/社用車の維持費 等))に換算しておくことで、人件費の変動や移動手段の異なる訪問先でも、お金という一元的な基準で判断することができます。

静止状態で評価する

　ゲームは対戦相手との連続操作が連なって局面が遷移していきます。その際、操作前後の変化で評価してしまうと状態管理が複雑になり、バグの温床になったり再現性が低下したりします。それを避けるため、操作後の局面だけ=静止状態で評価することを推奨します。
　これまでの評価関数の例は、すべて置いた石の状態を評価しているので問題ありませんが、例えば、四隅に置いてない状態から四隅に置いたら加点のような、変化や操作自体を評価することは避けた方がよいでしょう。

　実社会の例では、顧客を訪問した行為に加点するのではなく、既に訪問済の顧客数という状態に加点することが該当します。こうすることで、例えば複数人のセールスマンが顧客先を手分けして訪問する際、セールスマンが帰社してから評価を実施=非同期処理が可能になりますし、実は同一顧客を重複して訪問していた場合も不適切な加点を防ぐことができます。

トレードオフの関係に注意する

　対戦ゲームとして成立するものは、ある操作はそのリターンに応じたリスクが生じるように上手くゲームデザインされていることが多いです。そのため、作成した評価関数にて、ある観点を考慮しているが、それとトレードオフの関係にある観点を考慮できていない場合、相手にその隙を突かれて負けてしまうでしょう。それを避けるため、ある観点を加える際は対応するリスクが無いかよく考え、合わせて評価関数に組込むことを意識しましょう。
　リバーシでわかりやすいのは序盤の石の獲得です。リバーシは直線上の敵石を一気に自石に変えることができるため、ひっくり返される可能性の高い序盤石はなるべく数を抑える方が良いとされています。最終的には石の数を相手よりも多く取ることが重要ですが、序盤は獲得を抑え、どこで数を確保しに行くのか戦略性が問われるゲームであることが、長年愛されている理由なのだと思います。評価関数では、確定石(ひっくり返される可能性の無い石)の概念を導入すると良いでしょう。

// 観点を定めた評価関数
評価 = (確定自石 - 確定敵石) - (未確定自石 - 未確定敵石) 
       + 21 * (四隅の自石 - 四隅の敵石)
       - 10 * (未置四隅の周囲の自石 - 未置四隅の周囲の敵石)

　実社会の問題になると少々複雑です。模範的な巡回セールスマン問題では、基本的に訪問先が決まっており移動距離を最小化するか、特定のコスト内で訪問先数を最大化する問題となっていることが多いです。では、実際のビジネスでもセールスマンを大量に雇用に、訪問先を可能な限り増やすのが良い選択でしょうか？もちろん違います⁴。訪問先の企業の特性(規模やこれまでの関係等)に応じて、営業時に期待できる効果は異なります。セールスマンのスキルレベルも異なり、教育コストも無限にかけるわけにはいきません。そのため、期待値の高い顧客に一定のスキルレベルのセールスマンを向かわせることになり、必然的に手当たり次第の展開は評価が低くなることが導けます。

余談：AI⁵との関係

　Deep Learning の登場により、大量のデータからこれまで人手で定義しきれなかった緻密な分類木を自動で生成することが可能となり、実社会問題へのAI適用も当たり前のものになりました。分類木はある種の評価関数とみなすことが可能であり、実際にAlphaGoが強化学習によりプロ棋士を破ったことはご存知の通りです。
　自動で緻密な分類木を生成 = 自動学習、自動学習 = 強いAIだ！という極端な論調も見かけますが、現在はそこまで万能なものではありません。実社会のデータを取るのはコストがかかりますし、計算リソースもinput量に応じて指数的に増大します。現状は2つの条件を満たすからこそ上手く学習が進むと認識しています。

1. 上手く問題領域を切り出し学習対象データがある程度有用なものに絞られていること(=ゲーム)
2. 求める精度に応じた高精度・高密度・大量のデータが存在(完全シミュレート環境下で試行を繰り返せる(=ゲーム)ことも同義)

　Deep Learning の代表的な適用例である物体認識は上記を上手く満たす問題であり、特に視覚情報(イメージセンサ)のデータは他のセンシング可能なデータと比較して、桁違いの精度・密度を持つデータです。

　一方、上記の条件を満たせない領域に対しては、引き続き人間の仮説思考ベースのアプローチや結果の解釈が重要となり、人の手で評価関数を作ることは重要です。特に、最適化問題に類する社会問題の多くは、これまでの結果データが正解かというと必ずしもそうでないことが多く、また導出結果の解釈も重要であることから、局所的に Deep Learning を代表としたデータ学習アプローチを採用しつつ、全体としての評価は人の手でデザインすることが求められると考えています。

より良い評価関数を作るために

• 制約条件と区別する
• 異なる状態は異なる評価が付くようにする
• ビジュアライズして比べる

※内容については追って加筆します。すみません。すみません。

最後に

　ここまで読んで頂きありがとうございました。昨今、競技プログラミングの存在がIT業界で浸透した一方、その名称に引っ張られてか、プログラマーという一側面の評価ばかり注目されているように感じます。実社会をデジタルで捉える際、アルゴリズムの有識者とは、まるで白黒の映像をカラーで認識できるように、捉えられる情報量の次元が異なると考えています。この記事を通して、その片鱗を少しでも感じてもらい、実社会におけるアルゴリズム活用のきっかけの欠片にでもなれれば幸いです。

1. 筆者の年齢++。今年も投稿遅れて本当に申し訳ありませんでした。 ↩

2. 競プロへの入り口はいくつかあると思いますが、ゲームが好きでそこからゲームAIに興味を持つパターンがあると思います。私がそうです。 ↩

3. 探索木については過去記事を参照下さい。 ↩

4. 例に上げた最適化問題でも、現実世界では、路面の状況によって移動コストが違ったり、ナップサックへ入るかどうかは重量だけでなく品物の形状によっても変わります。 ↩ ↩²

5. 「AI」は特定の技術を指すものではありませんが、本記事では触れません。 ↩