MolGAN : An implicit generative model for small molecular graphs

はじめに

「機械学習の数理 Advent Calendar 2018」の18日目の記事です。

MolGAN : An implicit generative model for small molecular graphsについて読みましたので、纏めたいと思います。機械学習の数理というよりむしろ、手法の応用な所だと思いますがご容赦頂ければと思います。

※ 2023年6月16日：DDPGと数式表記を修正と一部校正をしました。なお、本論文は27 Sep. 2022に更新されています。

SMILESとは

本論文の説明に当たって機械学習以外に1つだけ知識が必要となりますので説明します。Wikipediaによると以下のようになっています。

SMILES (Simplified Molecular Input Line Entry System)は分子の化学構造をASCII符号の英数字で文字列構造の曖昧性のない表記方法である

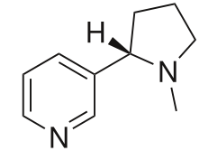
例えば、ニコチンは構造式だと下図になります。

化学式 : C10H14N2
SMILES : CN1CCC[C@H]1c2cccnc2

このグラフ構造を文字列で表したものがSMILESです。このような文字列表記にすることで、機械学習を用いることが容易になります。

分子におけるグラフ構造は、ノードが{C, N, H}の組み合わせであり、エッジは結合{単結合、二重結合}を表しています。この場合だと、ノード数は化学式の添え字個数から26, エッジ数は構造から24となります（水素を考慮）。

MolGAN概要

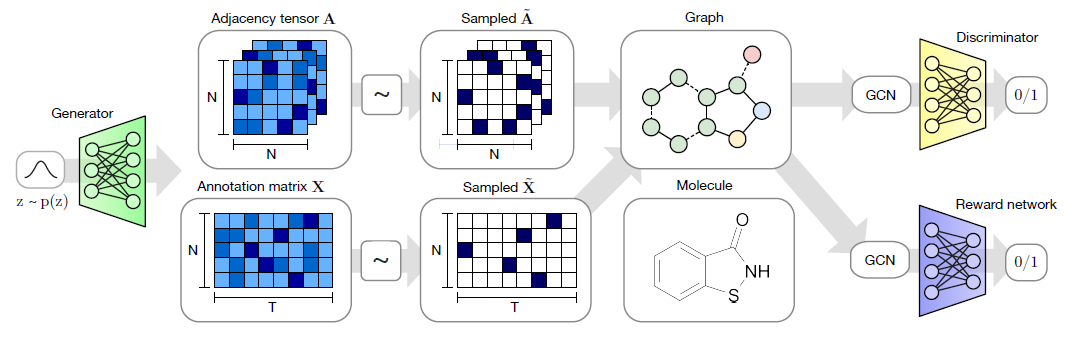
生成モデルであるGenerative adversarial network (GANs)と強化学習アルゴリズムであるDeep Deterministic Policy Gradient (DDPG)を用いて、目的の分子構造を自動生成することができるアルゴリズムとなっています。MolGANの特徴は、低分子がグラフとして一発で生成されるところです。

この図は、Generatorで分子構造を生成し、DiscriminatorでデータセットとGeneratorを識別します。この時、Generatorで生成された分子はReward Networkで評価されるアルゴリズムとなっています。

分子構造（すなわちSMILES）を生成させるような手法は、様々な方法があります。下記の方法が良く用いられる方法です。

• RNN (LSTMやGRU)を使ってSMILESを生成
• VAE
• GAN

特定の性質を持った分子を生成するために、モンテカルロ木探索（MCTS）や強化学習などもよく利用されます。

各種理論

化学構造は無向グラフで表すことができます。グラフ$G$, エッジ$E$, ノード$V$、それぞれの原子ノードを$\upsilon_i \in V$とします。また、ノードの属性を$T$次元のone-hot vector $x_i$とすれば、グラフ上ので原子の種類（C, H, Nなど）を表現することができます。結合情報はエッジ$(\upsilon_i, \upsilon_j) \in E$と表され、結合の種類$y \in \{1, ..., Y\}$に関連付けられます。

GANのような生成モデルを創薬のために用いるためには、合成可能かつ有用な活性、物性値を持った化合物を生成する必要がありますが、これには強化学習がよく用いられています。

Generative adversarial networks (GANs)

GANの詳しい説明は、Adventカレンダー17日目のkzkadcさんのGANと損失関数の計算についてまとめたを参照いただくとして、ここでは軽く説明します。

• Generative model $G_\theta$ : 事前分布から新しいデータを生成するモデル
• Discriminative model $D_\phi$ : $G_\theta$の分布から生成されたものかサンプルから来たものかを識別するモデル

これらの目的関数はtwo playersにおけるmini maxゲームになっています。Stochastic Gradient Descent (SGD)で同時に学習できます。

\min_\theta \max_\phi \mathbb{E}_{x\sim p_{data} (x)} [ \log D_\phi (x)] + \mathbb{E}_{x \sim p_z (z)} [ \log \big(1 - D_\phi  (G_\theta(z)) \big)] 

MolGANでは、ミニバッチdiscriminationと収束性の高いimporved WGAN (WGAN-GP)を使用してます。

WGAN

WGANs (Arjovsky et al., 2017)は、2つの確率分布間で定義されたEarth Mover距離 (これはWasserstein計量の1次元の場合)の近似を最小化させるような最適輸送の問題です。1次のWasserstein距離の最小化は、Kantrovich-Rubinsteinの双対表現により以下に示す最大化問題を解くことで近似できます。

D_{W} [ p || q] = \frac{1}{K} \sup_{||f||_L < K} \mathbb{E}_{x \sim p(x)} [f(x)] - \mathbb{E}_{x \sim q(x)} [f(x)]

なお、２つの確率分布の距離を測るのにKL divergenceがありますが、Wasserstein metricでは、次元の異なる分布の確率分布のメトリックを測ることができます。また、最適輸送の問題を解く際に、Sinkhornアルゴリズムを用いると、効率よく近似解を得ることもできます。

WGANの例では、$p$は経験分布で$q$がgenerator分布です。Lipscitz関数は、関数の連続微分可能性より強い形の連続性を有するような関数です。グラフ上の任意の2点を結ぶ直線の傾きの絶対値はある定数$K$を超えないような関数になっています。すなわち、この上界（supremum）がK-Lipschitz定数です。

d_Y (f(x_1), f(x_2)) \leq K d_X (x_1, x_2) \hspace{1cm}(\forall x_1, x_2 \in X)

さらに連続性を一般化させたものはヘルダー関数です。WGANでWasserstein距離が用いられているのはJensen-Shannon divergenceよりも最適化しやすいためです。パラメタライズされた関数$\{f_w\}_{w \in \mathcal{W}}$に対して次のよう定式化します。

\max_{w \in \mathcal{W}} \mathbb{E}_{x \sim p_{r}(x)} [f_w(x)] - \mathbb{E}_{z \sim p_{\theta}(z)} [f_w (g_\theta (z))]

このリプシッツ関数$f_w$をニューラルネットワークで近似していくことになります。これがdiscriminatorであり、Wasserstein距離の計算を表しています。$g_\theta$がgeneratorです。Wasserstein距離を最小化させるようなパラメータ$\theta$を求めるためにWasserstein距離を$\theta$で微分します。

\begin{align}
\nabla_{\boldsymbol \theta}W( P_r, P_{\theta}) &= -\mathbb{E}_{z \sim p(z)}\left[\nabla_{\boldsymbol \theta} f(g_{\boldsymbol \theta}(z))\right] \\
&\simeq \frac{1}{M}\sum_{m=1}^M \nabla_{\boldsymbol \theta}f\left(g_{\boldsymbol \theta}(z^{(m)})\right)
\end{align}

Mはバッチ数です。また$f_w$をリプシッツ関数にするため、$w$ ← clip(w, -0.01, 0.01)とさせます。$(w, \theta)$いずれの学習にもRMSPropを用います。

Improved WGAN(Gulrajani et al. (2017))では、gradient penaltyとして1-リプシッツ連続の緩い束縛条件を導入し、勾配のクリッピングを適用して、さらに改善しています。WGAN-GP (Gradient Penalty)とも呼ばれています。Generatorに関するlossはWGANと同じまま、discriminatorに関する誤差を下式のように修正しています。

L(x^{(i)} , g_\theta (z^{(i)}; w)) = - f_w (x^{(i)}) + f_w (g_\theta (z^{(i)})) + \alpha (|| \nabla_\hat{x}^{(i)} f_w (\hat{x}^{(i)}) || - 1)^2

第1項＋第2項がオリジナルのWGANであり、第3項目の勾配ペナルティ（gp）正則化が特徴です。

ここで、$\alpha$はハイパーパラメータ、$\hat{x}^{(i)}$は$z^{(i)} \sim p_z(z)$における$x^{(i)} \sim p_{data}(x)$と$g_\theta (z^{(i)})$間のサンプリングされた線形和となります。

\hat{x}^{(i)} = \varepsilon x^{(i)} + (1-\varepsilon) g_\theta (z^{(i)})　\\
\varepsilon \sim \mathcal{U}(0,1)

Deep Deterministic policy gradient (DDPG)

Deep Deterministic Policy Gradient(DDPG)はDQNの連続版です。DQNでは、行動は離散値しか利用できません。DQNではベルマン方程式の誤差を最小にすることで、最適な行動価値関数$Q^{\ast}(s, a)$を推定しようします。仮に、最適な行動価値関数$Q^{\ast}(s,a)$を知っているなら、どのような状態$s$が与えられても、最適な行動$a^{\ast}(s)$は以下の最適化問題を解くことで得られます。

a^{\ast}(s) = \arg \max_a Q^{\ast}(s, a).

DQNでは行動が離散なので、最適な行動$a^{\ast}$を選ぶのは簡単です。一方、$a$が連続値である場合は、都度最適化問題のサブルーチンを解く必要があり実用的ではありません。

そこで、DDPDでは、方策$\pi(a|s)$を決定的にし、$Q$関数と方策の最適化を交互に組み込むことで、連続値の行動を求めることができるようにした方法です。パラメータ$\theta$をもつ方策$\pi_{\theta}$を以下のように定義します。

a \sim \pi_\theta (s) = p_{\theta} (a|s)

これは状態$s$での行動$a$を選択する条件付き確率分布を表しています。一方、決定的な方策は下式のようになります。

a = \mu_\theta(s)

これは、状態$s$で行動$a$を出力するという決定的方策となっています。DDPGでは、$Q$関数を近似するネットワークと、方策を求めるネットワークを組み合わせることで、$Q$関数と行動が得られるようになります。

\max_a Q(s,a) \approx Q(s, \mu(s))

DDPGの概略図を示します。

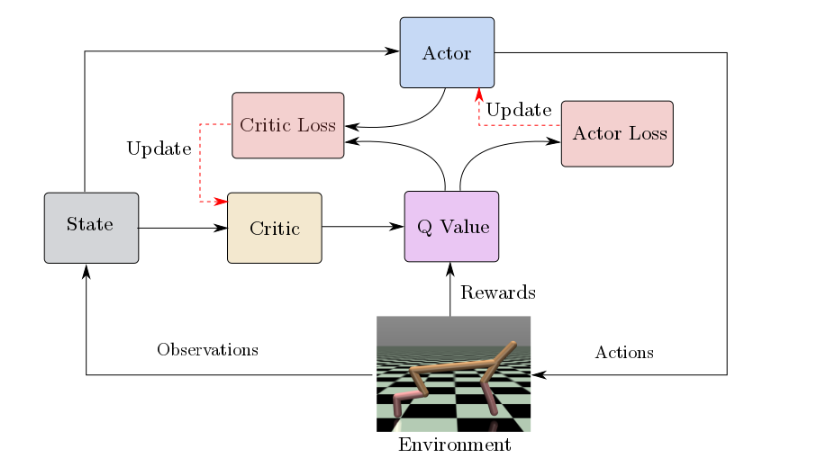
Actor-Criticと似ていますが、学習方式が異なります。

1. Actor network (Policy network: $\mu_{\theta}(s_t)$)
   Critic networkによって更新された行動価値関数$Q_w(s, a)$に基づき、方策$\mu_{\theta}(s_t)$の重み$\theta$を更新し、この方策から行動を決定します。このときは交差エントロピーを最小化（尤度の最大化）させるように学習させます。

2. Critic network (Q-value function: $Q_w(s, a)$)
   Actorの行動を批判します。すなわち、状態$s_t$, 行動$a_t$での報酬推定値（行動価値関数$Q(s_t, \mu_{\theta}(s_t))$）と即時報酬$R(s_t, \mu_{\theta}(s_t))$の2乗誤差（TD誤差、Mean squared Bellman error (MSBE)）を計算します。この勾配を用いて、Q関数のパラメータ$w$を更新します。それぞれ交互にactorとcriticを学習させモデルを更新していくいきます。

これらを式で書くと下式のようになります。

\begin{align}
\nabla_\theta &= \alpha \nabla_\theta  \log{ \mu_{\theta} (s_t)} \hat{Q}_w \left(s_{t},  \mu_{\theta}(s_t)\right) \\
\nabla_w &= \beta \left(R(s_t, \mu_{\theta}(s_t)) + \gamma \hat{Q}_w (s_{t+1}, \mu_{\theta}(s_{t+1})) - \hat{Q}_w (s_t, \mu_{\theta}(s_t))\right) \nabla_{w} \hat{Q}_w (s_t, \mu_{\theta}(s_t))
\end{align}

ここで、$\alpha$はactorの学習率、$\beta$はcriticの学習率、$\gamma$は割引率です。

DDPGの特徴

Experience Replay: $Q^{\ast}(s, a)$を近似するDNNを学習する際に利用される方法です。学習を進めていくと、価値関数や方策関数値の相関が高くなってしまい、$Q^{\ast}$関数の近似値のバリアンスが大きくなり、学習が不安定なってしまいます。このような問題を回避するために、エージェントの様々な経験をバッファーに保存し、シャッフルし、それを用いる工夫が施されています。学習を安定させるために、どの程度バッファーに保存するかなどハイパーパラメータとして調整する必要があります。

Target network: 直接、TD誤差から得られた勾配と共にactorとcriticのニューラルネットワークの重みを更新すると発散するか学習が進みません。そのため、学習の安定性が増すためにTD誤差のターゲットを生成するネットワークを用います。Critic networkの損失関数は下式となります。

\begin{align}
\text{target}_t &=  r + \gamma \max_{a_{t+1}} Q_{w_{\text{targ}}} \left(s_{t+1}, \mu_{\theta_{\text{targ}}} (s_{t+1})\right) \\
L(w) &= \frac{1}{N} \sum_t \bigg(\text{target}_t - Q_w (s_t, \mu_{\theta}(s_t) ) \bigg)^2
\end{align}

ここで、$N$はリプレイバッファからサンプリングされたミニバッチのサイズです。TD誤差の予測値であるTD targetは、「即時報酬$r$」と「critic networkから計算される報酬予測値（$Q_{\text{targ}}$値）」に割引率$\gamma$を掛けた和で計算されます。また、critic networkの損失関数$L$は先ほどのTD targetと行動$\mu_{\theta} (s_t)$ での $Q(s_t, \mu_{\theta} (s_t))$値からMSBE lossを計算し、最小化することで重み$w$を更新します。

また、target networkの重み$w$は、通常、過去のネットワークからコピーされます。DDPGでは、polyak averagingによってアップデートされます。

$$
w_{\text{targ}} \leftarrow \rho w_{\text{targ}} + (1-\rho)w
$$

ここで、$\rho$は0から1の間のハイパーパラメータであり、通常１に近く設定します。

一方、Actor networkではDeterministic Policy Gradientからのサンプリングを用いて重みを更新します。確率的方策勾配$\nabla_\theta \mu (a | s, \theta)$は方策のパフォーマンスの勾配であり、deterministic policy gradientはMarkov Decision Processでは下式となります。

\nabla_\theta \mu (a | s, \theta)  \approx  \mathbb{E}_{\mu'} \left[ \nabla_{a} Q_w (s, a) |_{s=s_t, a=\mu (s_t)}  \nabla_{\theta} \mu_{\theta} (s) |_{s=s_t} \right] 

期待値の方策項はactionに対する分布ではありません。必要なのは、ミニバッチに対する平均、パラメータに関するactor networkの結果の勾配を乗じた行動に対するcritic networkの結果の勾配だけです。

一方、本論文では、方策はgenerator $G_\theta$であり、インプットとしてサンプル$z$をとっています。これは強化学習での状態$s$に対応しています。アウトプットは分子グラフであり、行動$a = G_{\theta}(z) $に対応しています。また、Experience replayやtarget networksは用いられていません。

そのため、即時報酬を予測できる学習可能かつ微分可能な報酬関数$R_\psi$を導入しています。これは分子の合成可能スコア（Synthetic Accessibility）によって定義された平均2乗誤差関数です。

モデル

MolGANのアーキテクチャは主に3つから成っています。

• generator $ G_{\theta}$
• discriminator $ D_{\phi}$
• reward network $R_{\psi}$

分子グラフ

無向グラフの構造$G$を次のように定義します。ノード（原子）の属性を$T$次元のワンホットベクトル$x_i$、分子全体を表すためにアノテーション行列$\mathbf{X} = [x_1, ..., x_n]^T \in \mathbb{R}^{N×T}$とします。原子間の結合情報を表すため隣接テンソルは$\mathbf{A} \in \mathbb{R}^{N×N×Y}$です。ここで、$A_{ij} \in \mathbb{R}^Y$で$(i, j)$間のエッジの種類（{単結合、二重結合、三重結合、結合無し}）のワンホットベクトルです。

Generatorは事前分布$p(z)$からグラフを構成するのに必要な情報

• 隣接テンソル$\mathbf{A}$（エッジの属性と接続情報）
• アノテーション行列$\mathbf{X}$（ノードの属性）

を生成します。次にカテゴリカルもしくはGumbel-Softmaxに基づくサンプリングによりスパース構造のテンソル$\tilde{\mathbf{A}}$と行列$\tilde{\mathbf{X}}$がそれぞれ得られます。これらのグラフが化合物情報に相当します。生成されたグラフは、Relational-GCNのアーキテクチャを有するdiscriminatorやreward networkに入力され、生成されたノードの順序によらず識別や報酬関数の計算を行うことができます。

詳細

Generator: 事前分布からサンプリングされ、分子を表すannotated graph $G$が生成されます。ノードとエッジは、それぞれ原子と結合数でアノテーションされており、discriminatorはデータセットと$G$から生成したサンプルを識別します。$G_\theta, D_\phi$はimproved WGANを用いて学習され、generatorは経験分布と合うように学習することで最終的な結果として有効な分子が出力されるアルゴリズムとなっています。

Teward network: サンプルの価値関数を近似するために用いられ、強化学習を用いて微分不可能な指標に対し分子構造を最適化します。データセットや$G$のサンプルは$\mathcal{R}$のインプットですが、discriminatorと異なり、スコア（生成された分子の水に対する溶解性など）が与えられます。Reward networkはRDKitを用いて得られたスコアから学習します。有効でない分子の場合は報酬は与えられないようにしています。

Discriminator: WGANのlossと強化学習のlossの線形和を用いて学習しています。

L(\theta) = \lambda L_{WGAN} + (1-\lambda) L_{RL}

ここで$\lambda \in [0,1]$はGANと強化学習での生成モデルに対する2つコンポーネント間のトレードオフ（目的特性を重視するか有効な分子生成を重視するか）を調整するハイパーパラメータとなっています。$\lambda=0$なら完全な強化学習であり、$\lambda=1$ならGANによる生成モデルです。

Generator

$G_\phi (z)$は$z \sim \mathcal{N}(0,I), z \in \mathbb{R}^D$からサンプリングされたD次元のベクトルであり、アウトプットはグラフです。

Discriminatorとreward network

Discriminatorのreward networkのインプットはグラフ構造であり、アウトプットはスカラーです。ネットワークは同じアーキテクチャですがパラメータは共有しません。graph convolution層でグラフ隣接テンソル$A$を用いてノードのシグナル$X$を畳込みます。複数のエッジに対応するgraph convolution networkのRelational-GCN (Schlichtkrull et al., 2017)のモデルとしています。これはKnowledge baseのグラフであるので、すべてのレイヤーでノードの特徴表現は下式で畳込/逆伝播させることができます。

\begin{align}
h_{i}^{'(l+1)} &= f_s^{(l)} (h_i^{'(l)} , x_i) + \sum_{j=1}^N \sum_{y=1}^Y \frac{\tilde{A}_{ijy}}{|\mathcal{N_i}|}f_y^{(l)}(h_j^{(l)}, x_j), \\
h_i^{(l+1)} &= \tanh(h_i^{'(l+1)})
\end{align}

ここで、$h_i^{(l)}$はレイヤー$l$でのノード$i$のシグナルです。$f_{s}^{(l)}$はレイヤー間の自己結合のようにふるまう線形変換関数です。$f_{y}^{l}$はエッジに特異的なアフィン変換です。$N_i$はノードiの隣接するセットになります。

Graphの畳み込みを通じて各層は伝搬した後、ノードをベクターレベルのグラフ表現に埋め込むことができます。これは、Gated Graph Sequence Neural Network (GGS-NN)に従い行います。Readoutとも呼ばれます。

\begin{align}
h'_g &= \sum_{v \in \mathcal{V}} \sigma(i(h_v^{(L)}, x_v)) \odot \tanh(j(h_v^{(L)}, x_v)), \\
h_g &= \tanh (h'_g), \\
\sigma(x) &= \frac{1}{1 + \exp(-x)}
\end{align}

RGCNはMessage Passing Neural Network（MPNN）の特殊な例であると考えることができます。また、さらに一般化されたフレームワークはDeepMindのgraph_netsもあります。

tensorflowでは次のようになります。MPNNと対応できるように少し変更しています。

import tensorflow as tf


def mpnn_rgcn(inputs, units, training, activation, dropout_rate=0.,):
    adjacency_tensor, hidden_tensor, node_tensor = inputs
    graph_convolution_units, auxiliary_units = units

    # message passing
    with tf.variable_scope('graph_convolutions'):
        for unit in graph_convolution_units:
            adj = tf.transpose(adjacency_tensor[:, :, :, 1:], (0, 3, 1, 2))
            message = tf.concat((hidden_tensor, node_tensor), -1) if hidden_tensor is not None else node_tensor
            hidden_tensor = tf.stack([tf.layers.dense(inputs=message, units=unit) for _ in range(adj.shape[1])], 1)
            hidden_tensor = tf.matmul(adj, hidden_tensor)
            hidden_tensor = tf.reduce_sum(hidden_tensor, 1) + tf.layers.dense(inputs=message, units=units)
            hidden_tensor = activation(hidden_tensor) if activation is not None else hidden_tensor
            hidden_tensor = tf.layers.dropout(hidden_tensor, dropout_rate, training=training)

    # readout
    _, hidden_tensor0, node_tensor = inputs
    with tf.variable_scope('graph_aggregation'):
        if hidden_tensor0 is not None:
            message = tf.concat((hidden_tensor, hidden_tensor0, node_tensor), -1)
        else:
            message = tf.concat((hidden_tensor, node_tensor), -1)

        i = tf.layers.dense(message, units=auxiliary_units, activation=tf.nn.sigmoid)
        j = tf.layers.dense(message, units=auxiliary_units, activation=activation)
        output = tf.reduce_sum(i * j, 1)
        output = activation(output) if activation is not None else output
        output = tf.layers.dropout(output, dropout_rate, training=training)

    return output

実験条件

Generator architecture

• 最大ノード N = 9,
• 原子タイプ T = 5 (C, O, N, Fと one padding),　
• 結合タイプ Y = 5 (単, 二重, 三重結合, リング, 結合無し)
• Generatorは正規分布$\mathcal{N}(0,I)$から32次元のベクトルをサンプリング
• 3-layer MLP of [128, 256, 512]
• 活性化関数$\tanh$

Discriminator and reward network architecture

Generatorの出力は512次元になっているため、ノード、エッジをそれぞれ59=45, 59*9=405次元にした後、(5, 9), (5, 9, 9)にreshapeします。また、隣接テンソルは対称性があるので平均化させておきます。このグラフ構造をRelational GCN encoder with 2 layers [64, 32]で畳み込み計算します。その後、128次元のグラフ表現にし、2 layer MLP [128, 1] with tanhで計算しています。Reward networkではsigmoid functionを用いています。

評価指標

Samanta et alの論文中で利用される指標を使っています。分子が正しく生成できるか、データセットに存在しない分子を生成できるか、同じ分子を生成していないかなどを見るための指標です。

• Validity = 有効な分子数 / 全生成分子数
• Novelty = データセットに存在しない有効なサンプルセット数 / 全生成サンプル数
• Uniqueness = 生成されたサンプルのうち重複していない数 / 全生成サンプル数

結果

実際の論文のソースコードはgithubに公開されています。実際に実装してみたかったのですが、時間が足りませんでした・・・10 epoch試した結果を示します。

2018-12-17 20:38:53 Validation --> {'NP score': 0.926981851250385,
 'QED score': 0.49032351626089926,
 'SA score': 0.3339037990758661,
 'diversity score': 0.5755544722836816,
 'drugcandidate score': 0.4007257305767061,
 'la': 1.0,
 'logP score': 0.3475431831460153,
 'loss D': -114.99824,
 'loss G': 64.350525,
 'loss RL': -0.6873395,
 'loss V': 0.6542503,
 'novel score': 72.6204128440367,
 'unique score': 5.848623853211009,
 'valid score': 69.760000705719}

30 min位計算してみましたが、論文で出ているようなvalidスコアには全然なりませんでした。もう少し試したみたいですね。

MolGANの問題

強化学習をしているとmode collapseが発生します。また、正しいグラフはあまり生成されません。生成モデルから生成したグラフの隣接行列が正しいものでないため、2分子が生成されてしまいました。

グラフの学習方法を工夫する必要があるかもしれません。

おわりに

MolGANの要素技術についてまとめました。
生成モデル(WGANs)、強化学習(DDPG)、グラフ畳み込み（relational-GCN）と様々な方法が用いられています。こういった機械学習の方法を組み合わせ、活性の高い医薬品や新規化合物が合成できたら良いですね。

要素技術の実装部分があまり追えていないので、こちらも実装していきたいのと強化学習をどんどん試していきたいと思います。

Reference

• Cao and Kipf, MolGAN : An implicit generative model for small molecular graphs
• GANと損失関数の計算についてまとめた
• Arjovsky et al., Wasserstein Generative Adversarial Networks, 2017)
• Marco Cuturi, Sinkhorn Distances: Lightspeed Computation of Optimal Transport, NIPS2013
• Gulrajani et al., Improved Training of Wasserstein GANs, NIPS2017
• Silver et al., Deterministic policy gradient algorithms. In International Conference on Machine Learning, 2014.
• Deep Deterministic Policy Gradients in TensorFlow
• M. Schlichtkrull et al., Modeling Relational Data with Graph Convolutional Networks, arXiv preprint arXiv:1703.06103, 2017