ゲーム作りとかCGとかに関わる数学(初歩)②
この記事は2023年アドベントカレンダーの12/24の記事
の続きです。前の記事を読んでない人は前の記事を読んでおいてください。で、良ければいいねとストックもしておいてくださいw
前回は時間がないのと、数式多めのせいかブラウザが編集中に何度も落ちるので切りましたので、その続きを書いていきます。
今回のもブラウザが頻繁に落ち始めたらそこで切ろうと思います。やっぱり数式は負担が大きいのかな?
では、ベクトルの続きからやっていきましょう
ベクトルの続き…
2点を結ぶベクトルを作る
これは分かり切っているし、前回も説明してるのですが一応おさらいとこの後の話の伏線もこめてお話しします。
点Pから点Qに向かうベクトルを作りたいとします。このとき、これを覚えておいてください
「終点から始点を引く」
と。つまりPからQに向かうベクトルを作りたい場合は単純にQ-Pでいいわけです。
例えば$P=(P_x,P_y,P_z)$,$Q=(Q_x,Q_y,Q_z)$とするとベクトル$\overrightarrow{PQ}$は
\overrightarrow{PQ}=Q-P=(Q_x-P_x,Q_y-P_y,Q_z-P_z)
ですね。
この「終点から始点を引く」が2点を移動するベクトルだとすると、通常の座標点そのものもまたベクトルと言えますね?原点O=(0,0,0)とすると座標Pとは、原点から点Pへ移動するベクトル$\overrightarrow{OP}$と言えますし、同様に点Qは原点から点Qへ移動するベクトル$\overrightarrow{OQ}$と言えます
\displaylines{
P=\vec{P}=\overrightarrow{OP}=(P_x-0,P_y-0,P_z-0)\\
Q=\vec{Q}=\overrightarrow{OQ}=(Q_x-0,Q_y-0,Q_z-0)
}
と考えると、PからQに向かうベクトルとと言うのはベクトル$\vec{Q}$からベクトル$\vec{P}$を引き算したものであると言えますね。
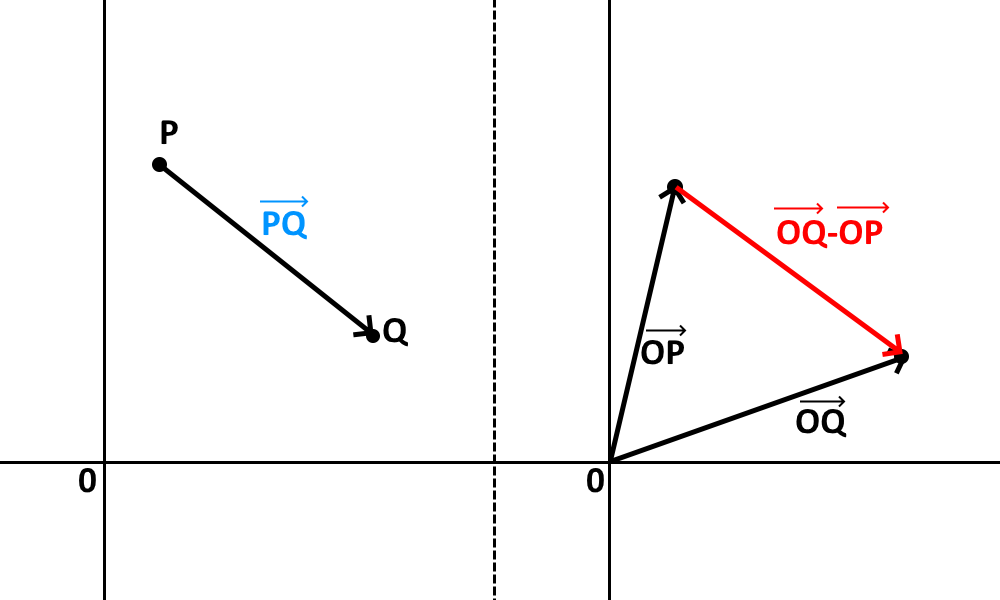
このことから座標そのものをベクトルとして扱ってもなんら差し支えないという事が分かりますね?ごくごく当たり前の事なのですが、大事な事です。
勿論プログラムでも
struct Vector3{//ベクトル
float x;
float y;
float z;
};
using Position3=Vector3;//座標(ベクトルと同じ)
と書いてもなんら問題ないわけです。どうせ3つの要素をまとめてるだけですし、演算も同じですし。
ベクトル自身への内積=ノルム²
これもごくごく当たり前のことですが、豆知識と言うか知っておいて欲しいというか、の話です。
前の記事でベクトルの内積を説明しましたが、あれ、自分自身との内積をとったらどうなるんでしょうか?
ベクトル$\vec{V}=(x,y,z)$とすると
\vec{V}\cdot\vec{V}=(x,y,z)\cdot(x,y,z)=x\times x+y\times y+z\times z=x^2+y^2+z^2=\|\vec{V}\|^2
というわけで、ベクトルの大きさ(ノルム)の2乗と等しくなります。当たり前の話なのですが、頭に入れておきましょう。
「球」もベクトルで表現できるよ?
さて、直前の話題で座標の引き算とベクトルのノルムの2乗について解説したわけですが、それを用いると球もベクトルでやたらとシンプルに表現できます。
さて、「球」ってなんでしょ?特定の点$P_c$からの距離が等しい任意の点Pの集合体です。(お分かりかとは思いますが、この点$P_c$は球の中心点です。centerの意で中心点の添え字をcにしています)
そう考えると、特定の点からのノルムが定数なのだから
\|\overrightarrow{P-P_c}\|=r
です。めっちゃ簡単な式で表せますね?これがベクトルの強みですね。これ両辺を二乗すると結局
\displaylines{
\|\overrightarrow{P-P_c}\|^2=r^2\\
\overrightarrow{P-P_c}\cdot\overrightarrow{P-P_c}=r^2\\
(x-x_c,y-y_c,z-z_c)\cdot(x-x_c,y-y_c,z-z_c)=r^2\\
(x-x_c)^2+(y-y_c)^2+(z-z_c)^2=r^2
}
てな感じで見覚えのある球の方程式になります。
球と直線の交点(当たり判定)
ベクトル方程式で解いてみる
まず$P=P_0+Vt$と$|P-P_c|=r$に交点があるかどうかを考えてみましょう。お分かりのようにこの点Pが一致するところがあれば「交点がある」となるわけですが、今回も変数はtのみです。
で、連立方程式を立てるとPの部分を$P_0+Vt$に置き換えて$|P_0+Vt-P_c|=r$
はい、まぁとはいえノルムなんでどのみち2乗しないといけないんですよね。面倒です。
面倒ですがx,y,zをバラバラで計算するよりマシです。
\displaylines{
\|P_0+Vt-P_c\|^2=r^2\\
(P_0+Vt-P_c)\cdot(P_0+Vt-P_c)=r^2\\
P_0\cdot P_0+(V\cdot V)t^2+P_c\cdot P_c+2P_0Vt-2P_cVt-2P_0\cdot P_c=r^2\\
(V\cdot V)t^2+2((P_0-P_c)\cdot V)t+(P_c\cdot P_c + P_0\cdot P_0-2P_0\cdot P_c-r^2)=0
}
はい、見た目フクザツですが、$Ax^2+Bx+c=0$の形になっているので、中学校で習った判別式と解の公式が使えますね。
\displaylines{
D=b^2-4ac\\
x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}
}
なお、今回の場合はBの部分が2の倍数になっているので、もう少し簡略化できて
\displaylines{
D=b^2-ac\\
x=\frac{-b\pm\sqrt{b^2-ac}}{a}
}
の方を使う事が出来ます。
とすると
\displaylines{
D=\sqrt{((P_0-P_c)\cdot V)^2-V^2(P_0^2-2P_0\cdot P_c-r^2)}\\
t=\frac{-(P_0-P_c)\cdot V\pm\sqrt{D}}{V^2}
}
はい、簡略化して書いてるはずなのに、うんざりするくらいに面倒ですね。
float A=Dot(V,V);
if(A==0.0f){
return;
}
float B=Dot(P0-Pc,V);
float C=Dot(P0,P0)+Dot(Pc,Pc)-2*Dot(P0,Pc)-r*r;
float D=B*B-A*C;
float t[2]={};
if(D>=0){
t[0]=(-B+sqrt(D))/A;
t[1]=(-B-sqrt(D))/A;
}
プログラム的には事前にA,B,Cは計算しておいて変数に入れておくので、意外とプログラム的には難しくないんですが理屈として、分かりづらいですね(いやホンマはこれくらい我慢してほしいんやけど…)
というわけで、ワイが考えた画期的な「図で見て分かりやすい」当たり判定を紹介します。
作図から幾何学的に当たり判定して交点を求める
結論から言います。
ズバリ~~~~!!球体の中心から直線に垂線を下ろしてその長さを求めます。
なんのこっちゃ?って話かもしれませんが、まぁ落ち着いて下の図を見てください。
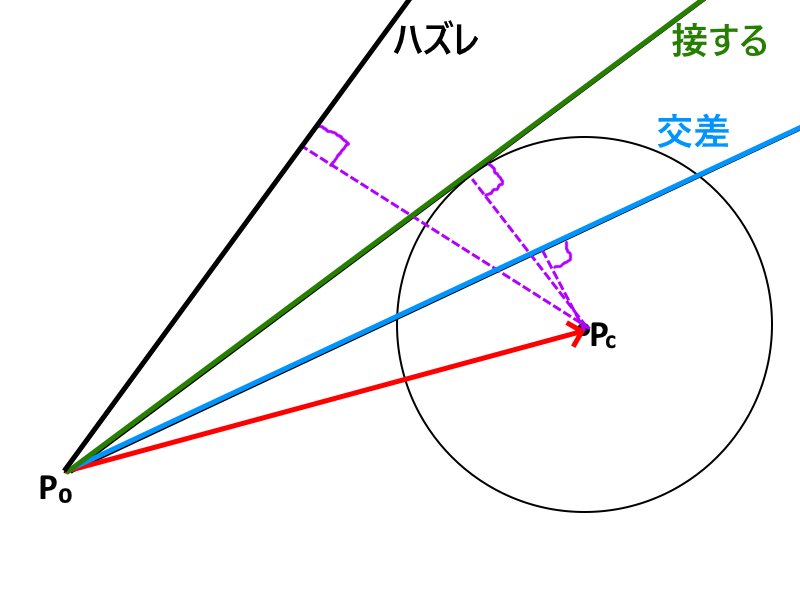
当たり判定はどう考えても垂線の長さに関連しているのが分かりますね?ちょうど「接する」の時が分岐点になっています。じゃあ、垂線と何の関係で決まるのでしょうか?そうですね「半径」です。
こうなります。
- 接する:垂線=半径
- 交差:垂線<半径
- ハズレ:垂線>半径
では垂線を求めていきましょう。ここで実はポイントになるのが図にしれッと書いてある「直線の基準点から球の中心点へのベクトル」です。
これを仮にベクトル$\vec{C}$としておきます。
で、「当たり判定」だけやるなら簡単で、外積でで求まります。
前回の外積の定義を見直しておいて欲しいんですが、
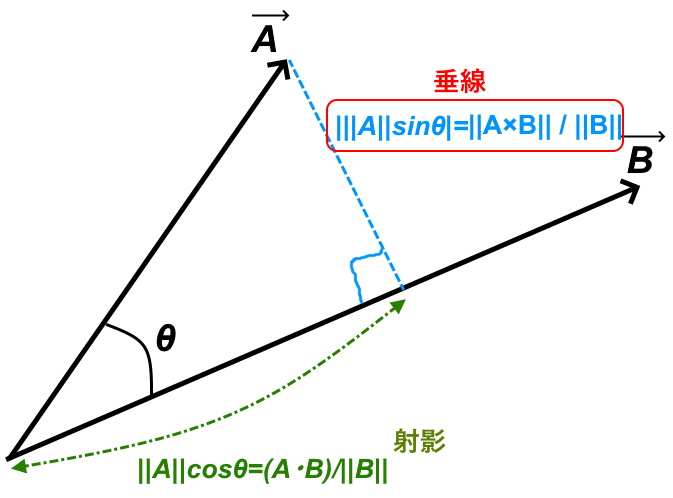
\|\vec{A}\times\vec{B}\|=|\|\vec{A}\|\|\vec{B}\|sin\theta|
こんな感じのことがちょろっと書いてたと思います。そう、3Dベクトルの外積って向き的には2つのベクトル双方に直交するベクトルになるんですが、その大きさ(ノルム)は|A||B|sinθなんですよね。内積と対になってる感じです。
これに関しては僕なりの考察があるので、あとでおまけで解説します。ともかくこれを使って垂線の長さを作ります。
両辺を|B|側で割ると垂線の長さになります。
で、当たる条件が
垂線≦半径
なわけだから
\frac{\|\vec{A}\times \vec{B}\|}{\|\vec{B}\|}\leqq r
が交差条件(接するも含む)となります。
プログラムで書くとこう…
//直線
stuct Line{
Position3 p0;//基準点
Vector3 vec;//方向ベクトル
};
//球体
struct Sphere{
Position3 center;//中心点
float r;//半径
};
bool IsHit(const Line& line,const Sphere& sp){
line.vec.normalize();//直線のベクトルを正規化しておく
Vector3 C=sp.center-line.p0;//基準点→球の中心
float vertLen=Cross(C,line.vec).Length();//外積ベクトルの大きさを取得
return vertLen<=sp.r;
}
と言う感じです。
でもこの外積を使うやり方、当たり判定は取れるけど交点が求めづらい(tを求めづらい)のよね・・・
ということで、ちょっとやり方を変えます。内積を使って求めます。ひとまず下図を見てください。
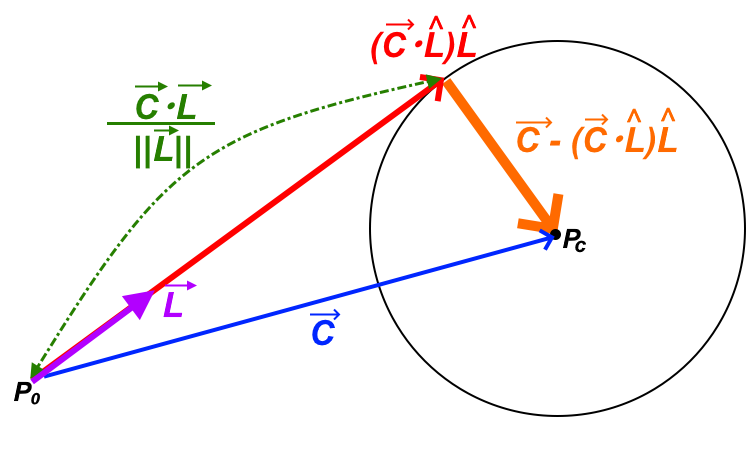
目的はオレンジのベクトルの大きさを求める事です。何で外積で求まったのにわざわざ回りくどく内積を使っているのかは後で解説します。
まず、直線と円の中心ベクトルと、円の中心から直線に下ろした垂線で直角三角形を作ります。
そうすると図のように、斜辺ベクトルが$\vec{C}$になります。
となると、垂線を下したところまでの長さは射影長と言えるので$射影長=|\vec{C}|cos\theta$になります。
計算を楽にするためにあらかじめ$\hat{L}=\frac{\vec{L}}{|\vec{L}|}$としておきます。そうするとベクトルの引き算を用いれば
\displaylines{
射影ベクトル=(\vec{C}\cdot \hat{L})\hat{L}\\
垂線ベクトル=\vec{C}-(\vec{C}\cdot \hat{L})\hat{L}\\
垂線長=\|\vec{C}-(\vec{C}\cdot \hat{L})\hat{L}\|\\
当たる条件:\|\vec{C}-(\vec{C}\cdot \hat{L})\hat{L}\|\leqq r^2
}
のように垂線ベクトルから垂線ベクトルの長さつまり垂線の長さが求まり、さらには直線と球が交点を持つかどうかが分かるわけです。
はい、外積を使ったら一発なのになんでこんなまどろっこしい方法で解いたのかと言うと、tを求めたい(交点までの距離を求めたい)からです。
ではガッツリ当たってる前提で今度は交点を求めてみましょう。基準点から交点までの距離tを求めてみたいと思います。
下の図を見てください。
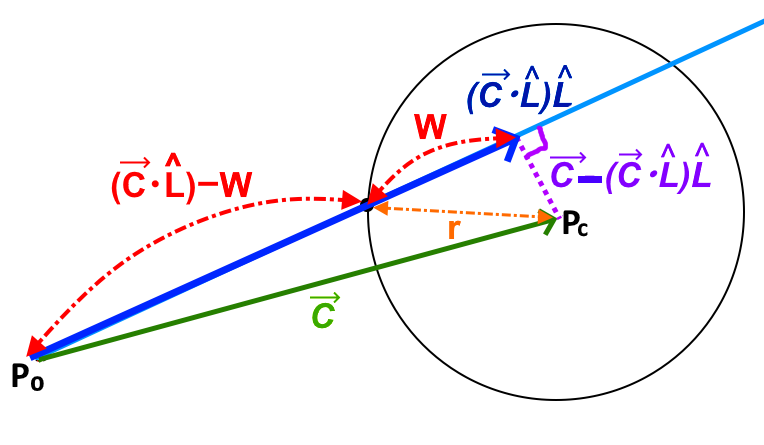
ちょっとごちゃついてますが、ゆるしてね。
まず、球体の中心から直線ベクトルに垂線を下ろしていますが、これは直線と球体の交点のちょうど真ん中になります。なぜなら半径は常にrなので、交点2つと中心点は二等辺三角形となり、垂線はそれを2分割するように引かれるからです。
基準点からそのちょうど真ん中までの距離は先ほど求めたように射影長つまり$\vec{C}\cdot\hat{L}$となります。
で、あとはこの垂線下ろした点から実際の交点までの距離を求めたいのですが、垂線長は分かってるのですからあとはピタゴラスの定理を用いれば求まります。
求めたい「垂線下ろした点から交点までの距離」を仮にWと置くとピタゴラスの定理より
\displaylines{
r^2=W^2+\|\vec{C}-(\vec{C}\cdot \hat{L})\hat{L}\|^2\\
W^2=r^2-\|\vec{C}-(\vec{C}\cdot \hat{L})\hat{L}\|^2\\
W=\pm\sqrt{r^2-\|\vec{C}-(\vec{C}\cdot \hat{L})\hat{L}\|^2}\\
t=\vec{C}\cdot\hat{L}+W
}
はい、Wに$\pm$がついてますが、これは接線になってない限り2つ交点があるためマイナスなら手前の交点、プラスなら奥側の交点までの距離となります。
ですから実際の交点は
P=P_0 + \hat{L}{(\vec{C}\cdot\hat{L}\pm\sqrt{r^2-\|\vec{C}-(\vec{C}\cdot \hat{L})\hat{L}\|^2}})
ぱっと見カッコの位置がちょっとややこしいですが、$\hat{L}(\vec{C}$のカッコが最後のカッコに掛かっています。
ともかくこれで交点が求まります。ひとまず手前の交点を返すプログラムを書きます。
//lineのvecは予め正規化しておく必要があります。
bool IsHit(const Line& line,const Sphere& sp,float& t){
Vector3 C=sp.center-line.p0;
float shadowLen=Dot(C,line.vec);//射影長
Vector3 shadowVec=line.vec*shadhowLen;
Vector3 vertVec=C-shadowVec;
float vertLen=vertVec.Length();
if(vertLen>sp.r){
return false;
}
float W=sqrt(sp.r*sp.r-vertLen*vertLen);
t=shadowLen-W;//手前の方だけ使う
return true;
}
(中略)
float t=0.0f;
if(IsHit(line,sp,t)){
//当たってたら座標を求める
Position3 P=line.p0+line.vec*t;
}
こんな感じですね。
カプセル形状の当たり判定
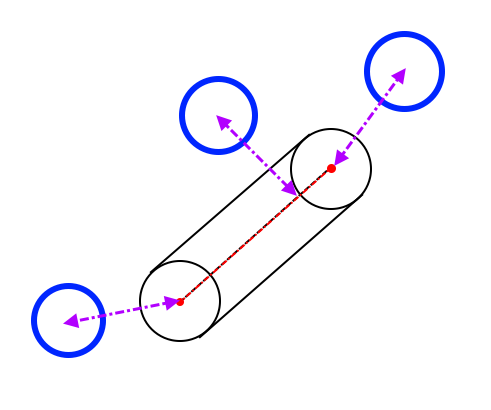
そもそも「カプセル形状」って何?って思われるかもしれませんが、UnityやUnrealEngineの基本形状のひとつで、同じ大きさの球体を2つ用意して、それを筒で包む感じの形状です。
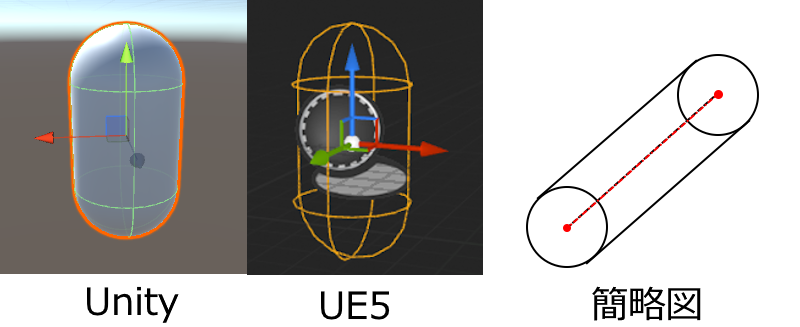
ある意味、球体をキューッと伸ばして、線分との距離がr(定数)の部分をなぞった感じになっているのが分かります。
この形状は当たり判定によく使用されるのですが、考えられる理由は
- 回転にも対応している(球体は回転しても変わらないし、直方体は回転すると面倒)
- 扱いやすい
- 計算が比較的楽
あくまでも「比較的」なんですけどね。何と比べてかというと直方体の回転であるOBB(OrientedBoundingBox)に比べればって話です。
球とカプセル形状の当たり判定
このカプセル形状との当たり判定で最も簡単なものは、球体に対してです。
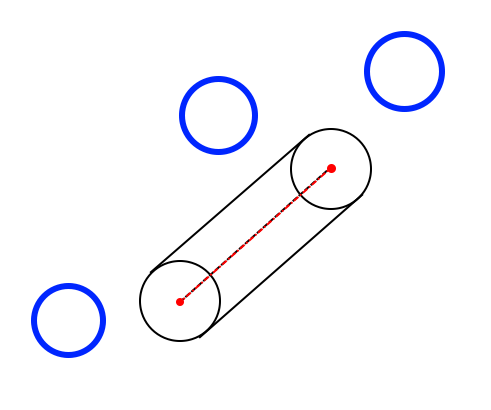
図は2Dで書いてますが、ベクトルを使えば3Dにも通用します。まず、それぞれの球体と線分の最短距離を考えます。これが求まれば半径+カプセルの太さ(カプセル半径)より距離が離れていれば当たらないのは分かりますね?
お気づきかなとは思いますが、線分の端点より遠いなら単純に線分の端点と球の中心点との距離が最短距離となります。つまり端点においては球体と何ら変わりないわけですね。
では、端点ではない所はどうかと言うと、最短距離=垂線です。垂線からちょっとでもズレるとピタゴラスの定理により必ず垂線より大きくなってしまいます。
と言う事は
- 端点では単純に点と点の距離を測る
- 線分上では垂線の長さを測る
ということになりますが、場合分け面倒ですね。もうちょっとなんとかならないものでしょうか?
この動画のように端点以外は垂線でついてきて、端点でピタッと止まるようにしたい。
言い換えると「範囲外に出たら端点の値にしたい」これはいわゆるクランプ関数ですね。C++にもstd::clampがあります。
じゃあ何をクランプすればいいのかと言うと、垂線ではなく射影長です。
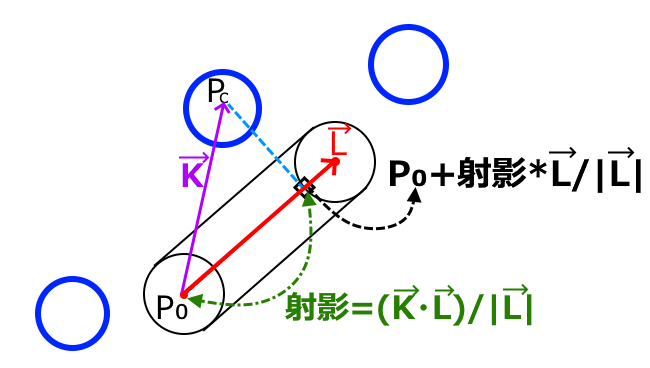
カプセル形状の端点の片方を仮に$P_0$とします。そしてもう一つの端点までのベクトルを$\vec{L}$とします。
球体の中心ベクトルを$P_c$とします。そして端点$P_0$から球の中心へのベクトルを仮に$\vec{K}$とします。
そうすると、垂線を下したところの座標は
P=P_0+\frac{{\vec{K}\cdot\vec{L}}}{\|\vec{L}\|}\frac{\vec{L}}{\|\vec{L}\|}=P_0+\frac{{\vec{K}\cdot\vec{L}}}{\|\vec{L}\|^2}\vec{L}
となります。
ここで「あれ?正規化してないの?」と思った人は鋭いですね。ふふふ・・・敢えてやってないのです。この後のクランプ作業のために。
ここで$\frac{\vec{K}\cdot\vec{L}}{|\vec{L}|^2}$の値について考えてみましょう。
仮に、$P_c$がもう一つの端点である$P_0+\vec{L}$の真上に来てたとします(要は垂線下ろしたところがそのまま$P_0+\vec{L}$と言う状態)。
そうすると射影長は$|\vec{L}|$になりますよね?と言う事は、先ほどの式が
\displaylines{
P=P_0+\frac{{\vec{K}\cdot\vec{L}}}{\|\vec{L}\|^2}\vec{L}\\
P=P_0+\frac{\|\vec{L}\|}{\|\vec{L}\|}\vec{L}
}
こんな感じになります。事実$P_0+\vec{L}$で正しいわけです。ここで注目すべきは$\frac{|\vec{L}|}{|\vec{L}|}$この部分です。当然1.0なんですが、これ今度は左端の場合だと0.0になるのは分かりますね?そもそも射影長が0なので。
つまり実はこの部分$\frac{\vec{K}\cdot\vec{L}}{|\vec{L}|^2}$が、元の線分の長さに対する射影長の割合を表しているのです。0.0だったら射影長0で、1.0だったら射影長$|\vec{L}|$です。
では、射影長が端点の外側に来たとするとどうなるのかと言うと、$P_0$側でない端点の向こうなら1.0<射影長となり、$P_0$側の向こうなら、射影長<0.0つまりマイナスになります。
ここでクランプを使うわけです。つまり
0.0\leqq\frac{\vec{K}\cdot\vec{L}}{\|\vec{L}\|^2}\leqq1.0
になるようにするわけです。最終的にそれに対して元の正規化していないベクトル$\vec{L}$をかけているわけですから、下の動画のように求める点が線分の外側に行けなくなるわけです(「追加解説用」の方を見てください)
あとはこの求めた点と円の中心をピタゴラスの定理で距離を測ればいいわけです。解説は2Dの図でしたが、このやり方は距離しか測っていないため、当然3Dでも使えます。
カプセルとカプセルの当たり判定[2D]
ちょっとここからは2Dと3Dでやりかたが異なるというか、3Dのほうがかなりヤヤコシイ話になるので、先に2Dの話からやっておきます。
2Dのカプセルどうしの当たり判定に関してはお互いの端点どうして最短距離を測ることで求められます。先ほどの「球とカプセル」の応用ですね。
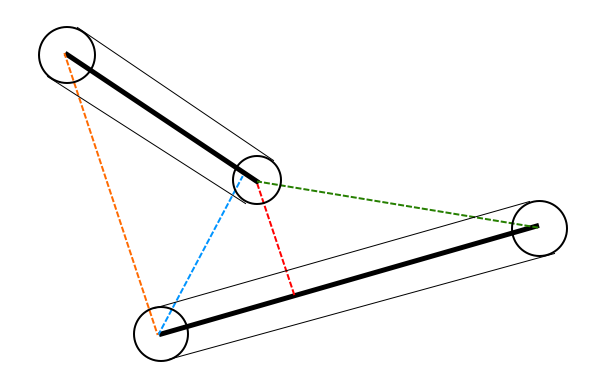
はい、線分が曲がってない限りはこの2つの線の長さのどれかが最短距離にあたるわけです。
円からカプセルに変わっただけで計算の手間が4倍になってますね。円の当たり判定がパフォーマンスに優れてる所以ですね。コードを書いてみます。円とカプセルを最初に書いておいて、それを利用したカプセルとカプセルの当たり判定を書きます。
//カプセルと円が当たったか?
bool IsHit(const Capsule& cap, const Position2& pos,float radius) {
//手順
//①まず、カプセル形状の端点cap.posAからccの中心点までのベクトルvpを作ります。
auto T = pos - cap.posA;//(ターゲットまでのベクトル)
//②次にカプセル形状そのもののベクトルposA→posBへのベクトルvを作ります。
auto V = cap.posB - cap.posA;
//③①と②の内積を求めます。
auto dot = Dot(T, V);
//④③の結果を②の大きさの2乗で割ります
auto f = dot / V.SQMagniture();
//⑤④の結果をクランプします
f = Clamp(f);
//⑥⑤の結果を②の結果にかけます
V *= f;
//⑦①のベクトルから②のベクトルを引きます
V = T - V;
//⑧⑦のベクトルの大きさを測ります
auto d=V.Magnitude();
//⑨⑧の値と、cap.radius+cc.radiusの値を比較します。
return d<=cap.radius+radius;
}
//カプセルとカプセルが当たったか?
//カプセルと円の当たり判定を4回行うだけ
bool IsHit(const Capsule& capA, const Capsule& capB) {
//手順
//①CapA.posA→CapBの最短距離
if (IsHit(capB, capA.posA, capA.radius)) {
return true;
}
//②CapA.posB→CapBの最短距離
if (IsHit(capB, capA.posB, capA.radius)) {
return true;
}
//③CapB.posA→CapAの最短距離
if (IsHit(capA, capB.posA, capB.radius)) {
return true;
}
//④CapA.posB→CapBの最短距離
if (IsHit(capA, capB.posB, capB.radius)) {
return true;
}
return false;
}
(※これだけだと、クロスした時に失敗しますので、下にある追記を見てね)
ここまでは簡単なんですよ・・・ここまではね・・・。
この後に3Dカプセルどうしの当たり判定に入っていくのですが、急に難しくなります。
記事も長くなってきてまたブラウザが落ち始めたので、一旦ここで区切ります。ちょっと予告編ですが
カプセルとカプセルの当たり判定(予告編)
- いきなり完成品を作るのは大変なので、まず直線(レイ)と直線(レイ)の当たり判定を行います
- 次に直線(レイ)とカプセルの当たり判定を行います
- 最後にカプセルの話の集大成としてカプセルとカプセルの当たり判定を行います。
次はマジでガッツリややこしいので、少し時間下さい。
それではお疲れさまでした。
追記(アップして30分くらいでさっそくご指摘が入りましたので…)
「ちょうどカプセルとカプセルがクロスしてる時に当たり判定外れるんじゃないですか?」
はい、その通りです。

ピャー、恥ずかちぃ~~~。
まぁ、とはいえ、あとはクロスの時さえ判定できれば大丈夫そうですね。ん?・・・クロス?クロス・・・?
あっ(察し)ということで、ここは外積を使ってクロス判定してみましょう。
2Dなので、外積関数はこうなります
///外積を返す
float
Cross(const Vector2& va, const Vector2& vb) {
return va.x*vb.y-va.y*vb.x;
}
で、この外積の特徴、前回の記事でも書きましたが計算順序で符号が変わります。2Dの時は得られるスカラー値の符号、つまりプラスマイナスが変わります。
今回はこれを利用します。
さて、どう利用するのか。線分どうしがクロスしてたらどうなるのでしょう?
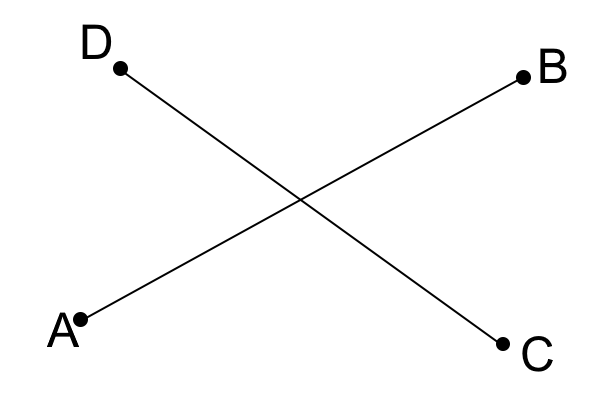
はい、図のようにAから見ると、もう一つの線分CDのCとDが線分ABによって分断されています。
これはCから見た場合、線分ABが線分CDによって分断されています。
これを両方満たせば「クロスしている」と言えるわけです。で、どうやって確かめればいいのでしょうか?ここで利用できるのが外積です。
順序で符号が反転するのを利用するわけです。う~ん、順序で符号が反転するというよりも
\displaylines{
\vec{A}\times\vec{B}=\|\vec{A}\|\|\vec{B}\|sinθ\\
\vec{B}\times\vec{A}=-\vec{A}\times\vec{B}=-\|\vec{A}\|\|\vec{B}\|sinθ=\|\vec{A}\|\|\vec{B}\|sin(-θ)
}
なので、乗算の向きによって符号が決定するわけですね。2Dで言うと乗算の順序が反時計回りならプラス、時計回りならマイナスってわけです(ゲームの2D座標系だとこれがまた逆になりますが、あまり気にしなくていいです)
先ほどの図の状況なら
\displaylines{
(\vec{A}\times\vec{C})(\vec{A}\times\vec{D})<0\\
(\vec{C}\times\vec{A})(\vec{C}\times\vec{B})<0
}
となるわけです。ところが
例えばこういう状況なら、
\displaylines{
(\vec{A}\times\vec{C})(\vec{A}\times\vec{D})>0\\
(\vec{C}\times\vec{A})(\vec{C}\times\vec{B})<0
}
このように外積をとると線分でぶった切られてる場合は符号が互い違いになるんですよね。これを利用します。
//カプセルとカプセルが当たったか?
bool IsHit(const Capsule& capA, const Capsule& capB) {
//手順
//①CapA.posA→CapBの最短距離
if (IsHit(capB, capA.posA, capA.radius)) {
return true;
}
//②CapA.posB→CapBの最短距離
if (IsHit(capB, capA.posB, capA.radius)) {
return true;
}
//③CapB.posA→CapAの最短距離
if (IsHit(capA, capB.posA, capB.radius)) {
return true;
}
//④CapA.posB→CapBの最短距離
if (IsHit(capA, capB.posB, capB.radius)) {
return true;
}
//⑤クロスしてる時
//AB×AD * AB×AC < 0 && CD×CA * CD×CB < 0
return Cross(capA.posB - capA.posA, capB.posA - capA.posA) *
Cross(capA.posB - capA.posA, capB.posB - capA.posA)<0.0f &&
Cross(capB.posB - capB.posA, capA.posA - capB.posA) *
Cross(capB.posB - capB.posA, capA.posB - capB.posA)<0.0f;
}
これでOK?
ご指摘してくれた人、本当に、ありがとう~~~!!
読者からの「こうしたらいいんじゃない?」投稿
また、別の読者さんからカプセルと球の当たり判定に関して別の解法を提示されました。
直線と球の当たり判定を応用します。ここでポイントになる考えは以下の通り
- 「厚みを持ったカプセルと球」ではなく、「線分と球」ただし球の半径は元の半径+カプセルの厚みとして計算する
- その球と直線の当たり判定を行い当たっていたら、得られた交点までの距離tが線分の端点の距離内に入っているかどうかを判定
ですね。コードにすると、こう
//直線と円の当たり判定
bool IsHit(const Position2& startPos, const Vector2& V, const Position2& center, float r,
float& t ) {
float A = Dot(V, V);
if (A == 0.0f) {
return false;
}
float B = Dot(startPos - center, V);
float C = Dot(startPos, startPos)+ Dot(center, center) - 2 * Dot(startPos, center) - r * r;
float D = B * B - A * C;
if (D < 0) {
return false;
}
t=(-B - sqrtf(D)) / A;
if (t < 0.0f) {
t = (-B + sqrtf(D)) / A;
if (t < 0.0f) {
return false;
}
}
return true;
}
bool IsHit(const Capsule& cap, const Position2& pos, float radius) {
//手順
//カプセルの厚みと円の半径を足した「新しい半径」を計算します
float r = radius + cap.radius;
//線分のベクトルを正規化します
auto segVec = (cap.posB - cap.posA);
auto segVecN = segVec.Normalized();
float t = 0.0f;
//直線との当たり判定
if (!IsHit(cap.posA, segVecN, pos, r, t)) {
return false;
}
if (0.0f <= t && t <= segVec.Magnitude()) {
return true;
}
return false;
}