1.はじめに
傘寿達成😂 内祝記念投稿🎉
MATLAB の三次元プロットには長年お世話になってきました。ところが、視線関連のコマンドやプロパティについては、view や Projection 以外には使った経験がありません。しかも、理解不十分のままで誤用までしていました。例えば、裸眼立体視のグラフの作成を、view の 方位角が異なる2つの画像を横に並べるだけで済ませていました( → MATLABで裸眼立体視 - Qiita)。しかし、実は、それだけでは左右の画像の大きさが微妙に異なるので完璧ではなかったのです。
これ以外にも見逃している重要なことが沢山ありそうで気になります。そこで、今更ながらではありますが、視線関連のコマンドやプロパティについて、マニュアル類だけに頼らず、実際に自分で使い込みながら細かく体験してみました。その結果を、個人的な解釈も交えながら詳しく解説してみようと思います。
動作確認環境: MATLAB R2019a( Toolbox なし )
2.各コマンドやプロパティの意味
2.1 コマンド一覧
MATLAB の視線関連コマンドには表1の左の欄に示すものがあり、これらとほぼ一対一の対応で、右隣りのプロバティが用意されています。「*」印が付いたプロパティには、それぞれに関連した CameraPositionMode, CameraViewAngleMode, CameraTargetMode, CameraUpVectorMode というプロパティもあり、auto(既定) と manual の2つの選択肢があります。ただし、「*」印のプロパティに具体的な数値を設定しさえすれば、それらの ………Mode プロパティは自動的に manual に変わるので、通常はそれほど気にすることはありません。auto に戻すときだけは ………Mode プロパティによる直接操作が必要になります。
なお、この記事では、一般には用いられていない独特の用語を使用する場合があります。既に使われている用語では定義が曖昧だったり、読み手によって解釈が異なったり で真意が伝わりにくいことがあるためです。まずは、表1で使われている用語を次のように定義しておきます。
- 観察対象: 1つのグラフの座標(axes)上に描かれる点・線・面・テキストなどの総称。タイトル、座標タイトル・目盛数値などは含みません。(Object と同義語かも)
- 作図箱: 観察対象を包含する直方体の箱。各辺は $x,y,z$ 軸と平行。その大きさと位置は axis( [$x_{min}$ $x_{max}$ $y_{min}$ $y_{max}$ $z_{min}$ $z_{max}$ ] )で決まります。figure 上には、6角形(特別な場合には4角形)として投影されます。(Plot Box と同義語かも)
- 縦画角: 一般にいう画角は画面の対角線を見渡す視角のことです。しかし、MATLAB では、画面の高さに相当する視角が重要になるため、これを縦画角と定義しておきます。また一般には、画角の外側は視野外になって見ることができないというのが常識ですが、ここで使う縦画角は表示画像の拡大/縮小率を決めるためのもので、視野を制限するためのものではありません(詳細は後述)。
表1 MATLAB の視線関連コマンド
| コマンド | プロパティ | 意味 | 値 |
|---|---|---|---|
| view | View | 作図箱の中心から見た視点の方向 | $[\lambda, \phi]$ (度) |
| campos | CameraPosition * | 視点を置く位置の座標 | $[x,y,z]$ |
| camva | CameraViewAngle * | 視点から観察対象を見る縦画角 | $\theta$ (度) |
| camproj | Projection | 三次元から二次元への投影法 | orthographic/perspective |
| camtarget | CameraTarget * | 視線の先を指示する点の座標 | $[x,y,z]$ |
| camup | CameraUpVector * | 観察対象の上下方向を決めるベクトル | $[x,y,z]$ |
| camroll | --- | 観察対象を視線周りに回転させる角度 | $\varphi$ (度) |
| $\hspace{4em}$ | $\hspace{8em}$ | $\hspace{15em}$ | $\hspace{10em}$ |
(上の表の様式は ここ を参考にさせていただきました。)
表1にも、それぞれについての簡単な意味は付記しました。しかし、その詳細な機能まで文章だけで書こうとすると長くなってしまいます。まずは次に続くアニメーションを見て身体で感じ取ってください。
以降、文字数が少々多めにはなりますが、【コマンド名よりも意味が伝わり易い】プロパティ名を優先して使用することにします。この場合のプロパティの設定例や読み出しの例について、下記に簡単に示しておきます。
hax=gca; % 現在編集中の座標(axes)のハンドルを取得
hax.View=[-10,45]; % その座標の View プロパティを設定
hax.Projection='perspective'; % その座標の投影法を設定
a=hax.CameraPosition; % その座標の CameraPosition プロパティを変数 a に取得(a ← [x,y,z])
2.2 Projection
Projection で図の投影法を指定します。図1の左側が既定の orthographic(正投影法)、右側が perspective(透視投影法) です。第三角法の設計図を見慣れてきた人には、正投影法にもそれほどの違和感はありません。むしろ、平行な線同士はどこまでも平行に見える方が都合が良い場合もあります。しかし、図1のモデルで比べてみれば、やはり、目で見たとおりに自然に感じられるのは透視投影法です。そこで、本記事では、特に断らない限り、透視投影法の使用を前提にすることにします。また、この写実的な効果が自然に表現できるように、$\pmb{x,y,z}$ 全軸とも等スケール( axis equal )のグラフに限定して考えることにします。
図1では、Projection だけでなく、他の CameraPosition や CameraViewAngle プロパティも manual モードにしてその値を操作しています。しかし、ここでは細かな話は抜きにして、まずは、Projection の種類による効果の違いを目で見て感じていただくだけで十分です。
図1 Projection: 左=orthographic(正投影法), 右=perspective(透視投影法)
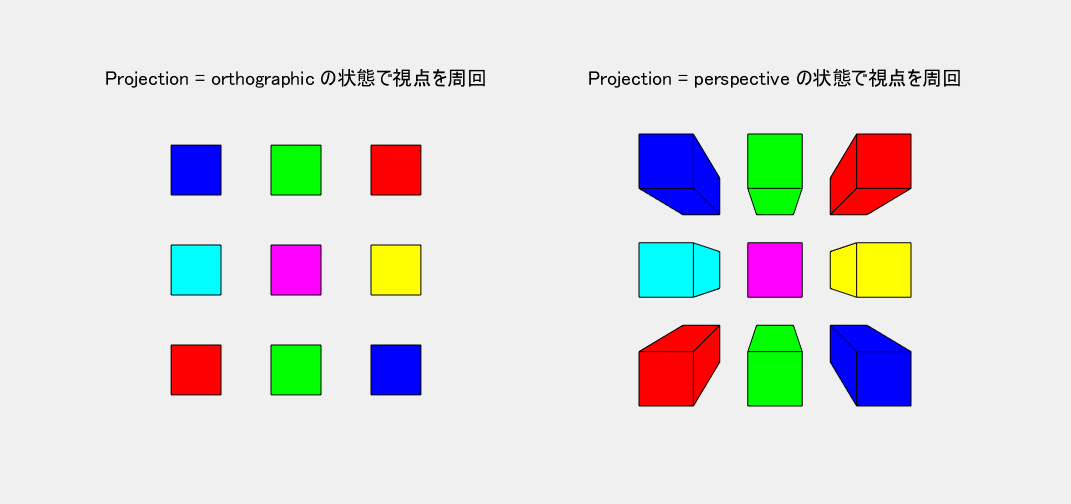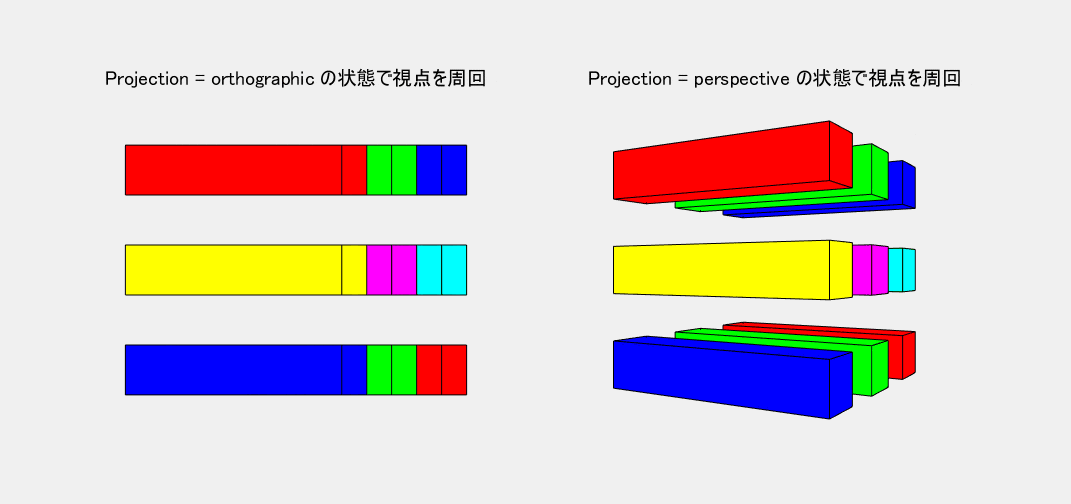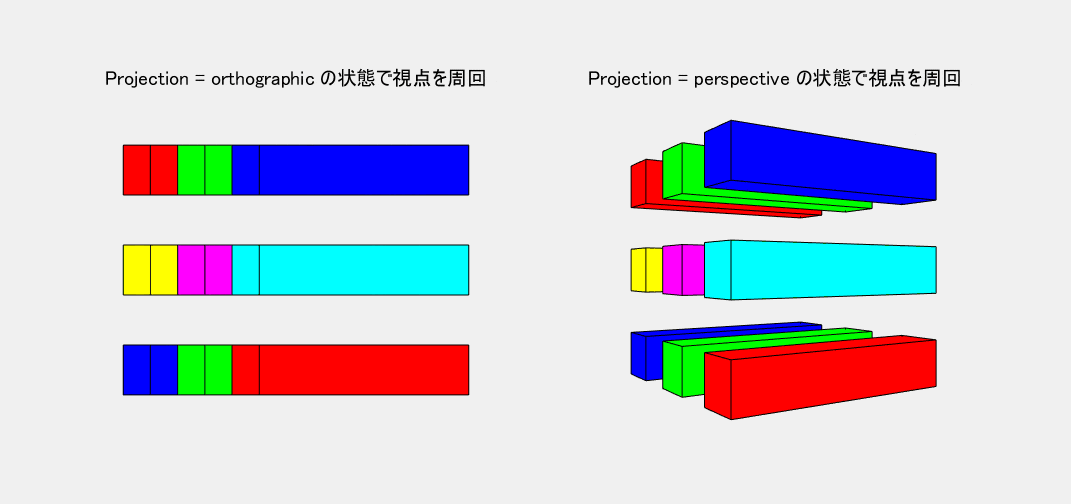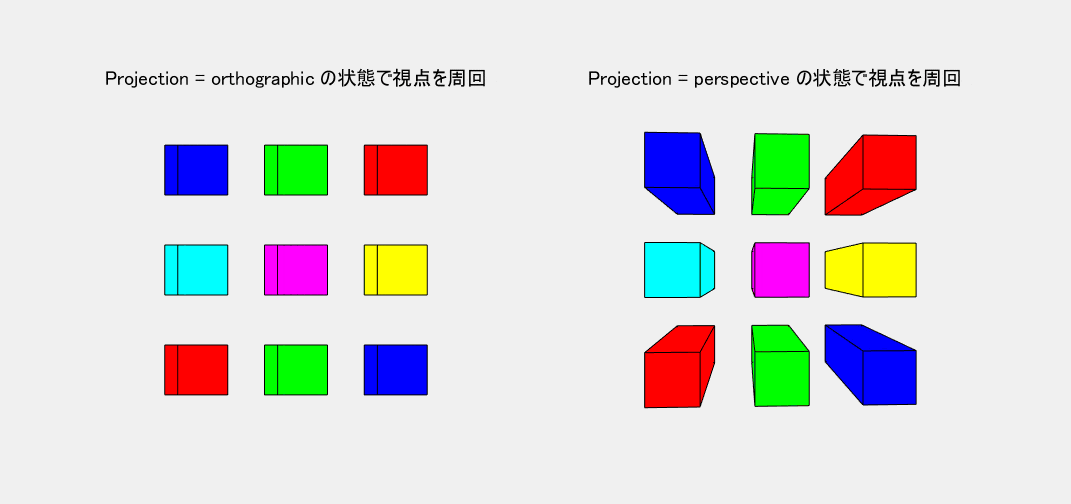
ヘルプセンターのドキュメンテーションの控えめな図では、両投影法の違いがあまりはっきりしません。しかし、図1を見れば、その差は明白です。
プログラム
図1を描画するプログラムを次に示します。
ここをクリックしてプログラムを開/閉
% view_point23.m
% Projection の 'orthographic' と 'perspective' の効果の違いを示すた
% めに、9本の角材群をモデルにして、azimuth を漸増させて回転させる
% 動画を作成。
clear
close all
% 1つの figure(hf) 内に、横並びの2つの二次元プロット用画面(ax3,ax4)
% を作る(ローカル関数の呼び出しによる)。
% ほぼ、それぞれの定位置にタイトルを表示するためだけの画面
[hf,ax3,ax4] = make_2_axes();
% それぞれの axes の上層に重ねて、同一サイズの axes を作る。
% ここにはメインの三次元プロットを表示する。
ax1=axes('Position',ax3.Position);
ax2=axes('Position',ax4.Position);
% ===============================================
% 角材1本の展開図データ
X=[0 1 NaN NaN NaN ;
0 1 1 0 0 ;
0 1 1 0 0 ;
0 1 NaN NaN NaN ];
Y=[5 5 NaN NaN NaN ;
5 5 5 5 5 ;
0 0 0 0 0 ;
0 0 NaN NaN NaN ];
Z=[0 0 NaN NaN NaN ;
1 1 0 0 1 ;
1 1 0 0 1 ;
0 0 NaN NaN NaN ];
% 9本の角材の配置位置と色
posx=[1 3 5 1 3 5 1 3 5]-1;
posz=[1 1 1 3 3 3 5 5 5]-1;
col={'r' 'g' 'b' 'c' 'm' 'y' 'b' 'g' 'r'};
% ===============================================
axes(ax1); % 左側の座標を開く
% 角材群を描画
for n=1:9
surf(X+posx(n),Y,Z+posz(n),'FaceColor',col{n});
hold on
end
axis equal
ax1.Projection='orthographic'; % 正投影法を指定
ax1.CameraViewAngle=31; % 縦画角は固定
axis(ax1,'off'); % 座標軸は非表示
hchild=get(ax1,'Children'); % 左側の図を取得(右側に貼り付けるため)
% 回転アニメのために必要なデータ Pcen, Lcam の準備
Ax=axis(ax1);
Xmin=Ax(1); Xmax=Ax(2); % 描画箱のX座標の最小値と最大値
Ymin=Ax(3); Ymax=Ax(4); % 〃 Y座標 〃
Zmin=Ax(5); Zmax=Ax(6); % 〃 Z座標 〃
Pmin=[Xmin Ymin Zmin]; % 描画箱の最小座標の頂点のベクトル
Pmax=[Xmax Ymax Zmax]; % 〃 最大座標 〃
DD=Pmax-Pmin; % 描画箱の Pmin からの対角線ベクトル
Pcen=Pmin+DD/2; % 描画箱の中心点を示すベクトル
Lcam=norm(DD)*1.5; % Pcen と Pcam の間の距離の指定値
% ===============================================
axes(ax2); % 右側の座標を開く
copyobj(hchild(:),ax2); % 左側の図を貼り付け
axis equal
axis(Ax); % axis は左の図と合わせる
ax2.Projection='perspective'; % 透視投影法を指定
ax2.CameraViewAngle=35; % 縦画角は固定。均衡を考え、やや大きめ。
axis(ax2,'off'); % 座標軸は非表示
% ===============================================
% View の azimuth を連続変化させて視点を周回。
az0=0; % azimuth 初期値
el0=0; % elevation(一定値)
azd=3; % azimuth の変化ステップ
% 1回転分のアニメ gif 動画を作成
filename = 'view_point23.gif'; % 動画のファイル名
delay=0.0417; % 一コマの秒数(24コマ/秒)
azim=[az0:azd:az0+359]; % azimuth を等間隔で変化。
for n=1:length(azim)
az=azim(n);
Pcam=Pcen+Lcam*[cosd(el0)*cosd(az-90) cosd(el0)*sind(az-90) sind(el0)];
ax1.CameraPosition=Pcam;
ax2.CameraPosition=Pcam;
drawnow;
frames=getframe(hf); % figure画像を取得。
[A, map] = rgb2ind(frame2im(frames), 256); % 画像形式変換
if n == 1
imwrite(A, map, filename, 'gif', 'DelayTime', delay, ...
'LoopCount',Inf);
% 表示はdelay秒間。1コマ目で繰返し再生回数の設定。
else
imwrite(A, map, filename, 'gif', 'DelayTime', delay, ...
'WriteMode', 'append');
% 2コマ目以降には、"追記"の指示が必要。
end
end
% その後、無限ループで連続回転させる。
disp('無限ループで実行中です。実行の停止は、Ctrl-C で。')
while true
az=az+azd;
if az>=180
az=az-360;
elseif az<-180
az=az+360;
end
Pcam=Pcen+Lcam*[cosd(el0)*cosd(az-90) cosd(el0)*sind(az-90) sin(el0)];
ax1.CameraPosition=Pcam;
ax2.CameraPosition=Pcam;
drawnow;
pause(0.05); % 0.05秒の休止
end
% ===============================================
% ローカル関数
% ===============================================
function [hf,axA,axB] = make_2_axes()
% 1つの figure 内に横並びの2つの画面を作って、
% それぞれのタイトルを表示する。
% まずは、作図の目安にするため、既定の axes のサイズを取得
hfx=figure(1);
hax=axes;
Pf=hfx.Position; Pa=hax.Position;
Wa=Pf(3)*Pa(3); % axes の既定の幅 [px]
Ha=Pf(4)*Pa(4); % axes の既定の高さ [px]
close(1); % 用済みの figure を削除
% 標準サイズより小さめの axes を準備
k=0.7; % axes の倍率
Wa=round(k*Wa); Ha=round(k*Ha); % 小さな axes の幅と高さ [px]
Mt=0.25; Mb=0.15; Ml=0.15; Mc=0.05; Mr=0.15;
% Wa,Ha の値をベースにした、figure 内の
% 上,下,左,中,右の margin。
% 中 margin とは axes 間の間隔のこと。
% 2つの axes を持った新しい figure を開く。
WT=2+Ml+Mc+Mr; % 新しい figure の幅と高さの見積もり
HT=1+Mt+Mb; % (Wa,Ha の値をベース)
hf=figure(1);
hf.Position=[100 50 Wa*WT Ha*HT]; % px 単位の figure の Position。
axA=axes('Position',[Ml/WT Mb/HT 1/WT 1/HT],'Color','none');
% 左側の axes の Position を設定
axB=axes('Position',[(Ml+1+Mc)/WT Mb/HT 1/WT 1/HT],'Color','none');
% 右側の axes の Position を設定
for n=[axA axB]
axes(n)
axis off
hold on
if n==axA
title('Projection = orthographic の状態で視点を周回')
else
title('Projection = perspective の状態で視点を周回')
end
end
end
2.3 View および CameraViewAngle
図1では、都合(perspective の効果を強調するため)によって CameraPosition を操作して図を回転させています。しかし、一般には View で回転させるほうが簡単で近道です。図2では、View の2要素( azimuth (方位角)、elevation (仰角) )のうちの azimuth を漸増させながら観察対象を回転させています(実際は観察対象は止まっていて、その周りを自分が周回しています)。この図では示していませんが、 elevation の方を操作すれば、観察対象を上から見下ろしたり、下から見上げたりすることができます。これらが View (視点がある方向) の機能です。
一方、CameraViewAngle(縦画角) の機能を示すために、左右2つの図にそれぞれ異なる条件を設定しています。左側の図では、CameraViewAngleMode を既定の auto のままにして CameraViewAngle の値を自動調整させています。右側の図では manual モードで CameraViewAngle の値をある一定値に固定しています。
なお、両図を囲む赤枠(以降も、この記事での専門用語として使用)は、二次元プロットにおいて、グラフ面(ただし、目盛数値やタイトルを除く)として確保される領域(axes)の縁(ふち)を示しています。通常の図ではこの赤枠は描かれません。CameraViewAngle の auto の効果を分かり易くするために特別に表示させています。
図2 View による作図箱周りの周回(CameraViewAngle: 左=auto / 右=一定値)
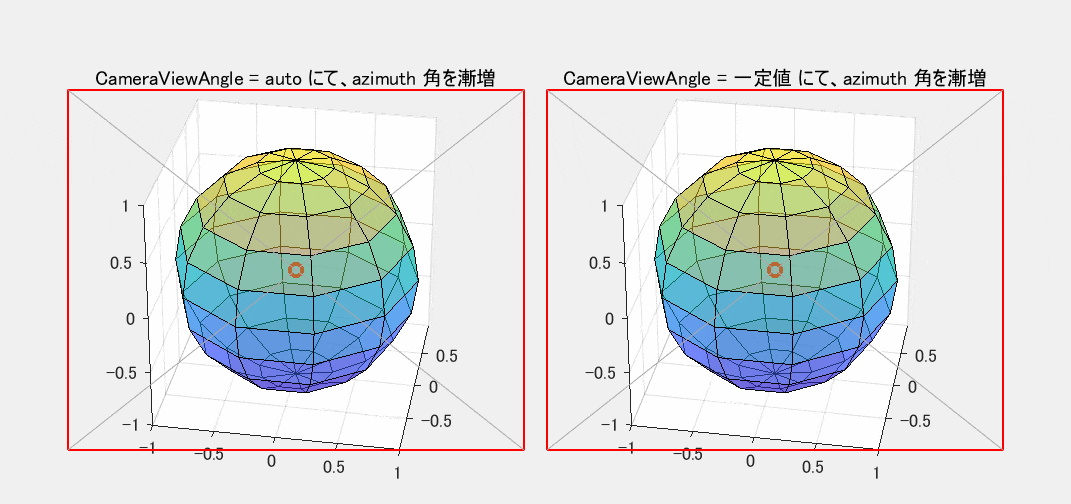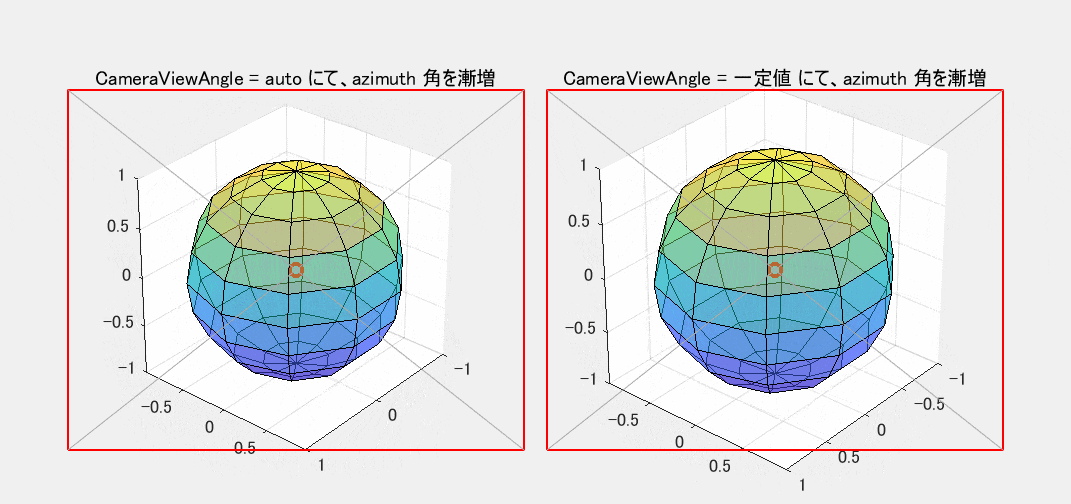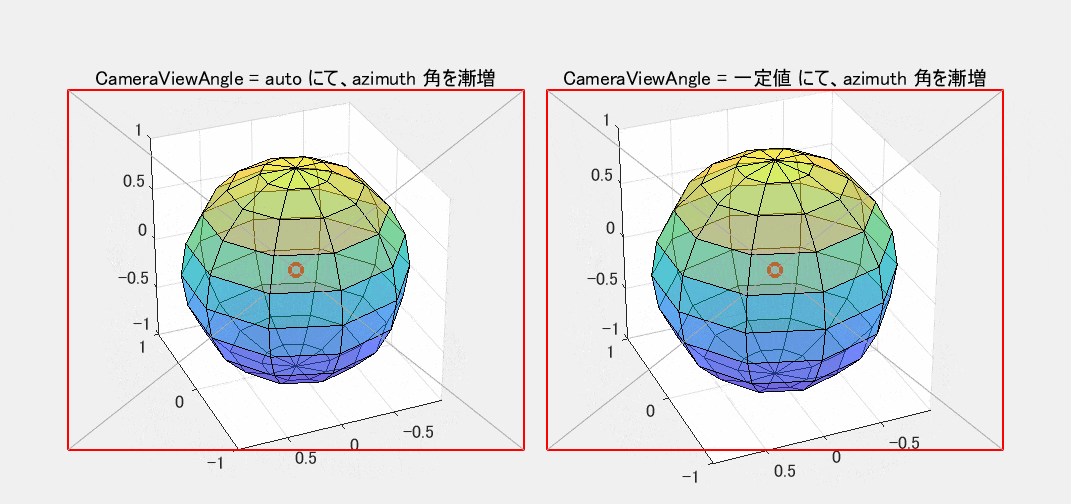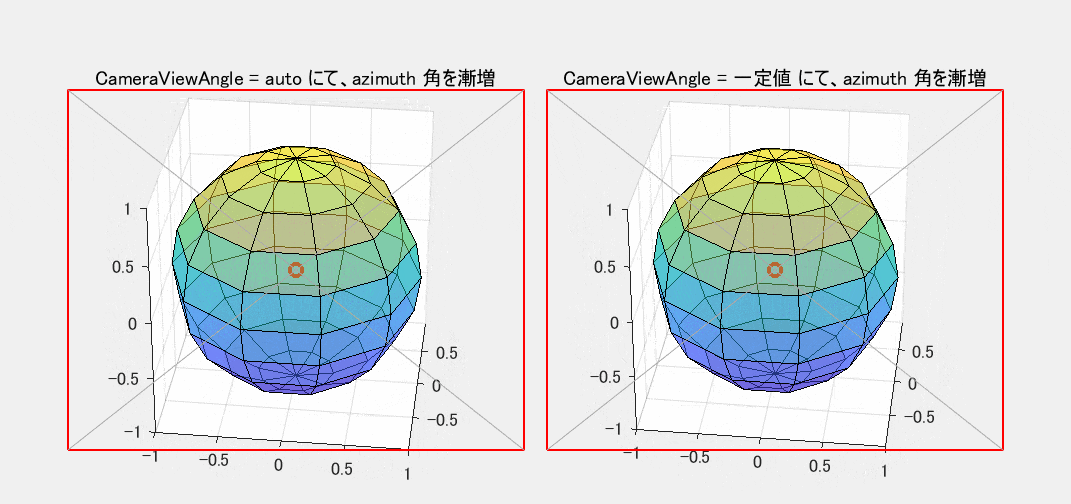
縦画角を固定した右側の図では、視点の方向 View を変化させても、観察対象の球の大きさは変わりません。縦画角が一定であれば、これが自然な動作です。
一方、左側の図では、観察対象の球の大きさが View の変化につれて変動しています。 CameraViewAngleMode が auto の場合、MATLAB は【作図箱が投影されて出来た多角形(白地の部分)】をできるだけ大きく表示し、かつ、赤枠内に完全に収まるように縦画角を自動調整します。左の図の動きを観察すれば、MATLAB のこの調整方針が読み取れるはずです。右側の図では、6角形の端が赤枠外にはみ出してもお構いなしです。
なお、左の図をさらに細かく観察すると、「多角形をできるだけ大きく表示する」といいながら、その下部は赤枠に接しているものの、上部にはまだ若干の伸びしろが有るように見えます。なぜでしょう?。実はもう一つの制約条件があります。すなわち、CameraTarget(視線の先の点。既定の auto では 作図箱の中心と一致する)は必ず赤枠の中心に置かなければならないという条件です。球体の内側にある赤〇印は作図箱の中心(既定では同時に CameraTarget でもある)を示しています。この〇印が、要求された条件によって、赤枠内の対角線の交点(赤枠の中心)に引き留められています。ここで、作図箱の上側の頂点は下側の頂点よりも遠方にあることに注意してください。透視投影法では遠方にある方が小さく見え、より中心に寄った位置に描かれて、赤枠の上辺との間に多少の余裕ができます。
CameraViewAngleMode は auto が既定であり、殆どの人はそのまま利用しているものと思われます。この縦画角の自動調整機能のおかげで、利用者は観察対象の規模の大小に煩わされず、常に自動的に、丁度良い大きさの図が描けて助かっています。ところが、「View を変えても大きさは変えたくない」という用途では、逆に、これが邪魔になってきます。しかし、解決法は簡単で、CameraViewAngle に適度な一定値を設定するだけでOKです。
プログラム
図2を描画するプログラムを次に示します。
ここをクリックしてプログラムを開/閉
% view_point11.m
% CameraViewAngle が auto と manual のそれぞれの条件で、
% View の azimuth を連続変化させたときの動画を作成。
clear
close all
% 1つの figure(hf) 内に横並びの2つの二次元プロット用画面(ax3,ax4)
% を作って、それぞれの axes いっぱいに赤枠を描く(ローカル関数の
% 呼び出しによる)。
[hf,ax3,ax4] = make_2_axes();
% それぞれの axes の上層に重ねて、同一サイズの axes を作る。
% ここにはメインの三次元プロットを表示する。
ax1=axes('Position',ax3.Position);
ax2=axes('Position',ax4.Position);
% ===============================================
[X,Y,Z]=sphere(10); % 球のデータ
axes(ax1); % 左側の座標を開く
surf(X,Y,Z,'FaceAlpha',0.5); % 球面の表示
axis equal
hold on
plot3(0,0,0,'or','LineWidth',2); % Pcen 相当の点に赤〇印
view([10 30]); % 既定の [-37.5 30] のままでは、manual モー
% ド側の図が小さめになるので、適度に変更。
ax1.Projection='perspective'; % 透視投影法を指示
% ===============================================
axes(ax2); % 右側の座標を開く
% 球面の表示
surf(X,Y,Z,'FaceAlpha',0.5); % 球面の表示
axis equal
hold on
plot3(0,0,0,'or','LineWidth',2); % Pcen 相当の点に赤〇印
view(ax1.View); % 左の図と同じ View に設定
ax2.Projection='perspective'; % 透視投影法を指示
va0=ax2.CameraViewAngle; % CameraViewAngle の初期値を取得。
ax2.CameraViewAngle=va0; % 初期値をそのまま不変値として設定する。
% 自動的に manual モードとなる。
% ===============================================
% 最下層の座標を ax2 とし、その上層に次の順で座標を重ねていく。
axes(ax1); % ax2 の図が大きくなっても、ax1 の図が隠されないように。
axes(ax4); % 赤枠やタイトルは最優先で常に表示されているように。
axes(ax3); % 〃
% ===============================================
% View の azimuth を連続変化させて視点を周回。
axv=ax1.View;
az0=axv(1); % azimuth 初期値
el0=axv(2); % elevation 値(一定)
azd=3; % azimuth の変化ステップ
% 1回転分のアニメ gif 動画を作成
filename = 'view_point11.gif'; % 動画のファイル名
delay=0.0417; % 一コマの秒数(24コマ/秒)
azim=[az0:azd:az0+359]; % azimuth を等間隔で変化。
for n=1:length(azim)
ax1.View=[azim(n) el0];
ax2.View=[azim(n) el0];
drawnow;
frames=getframe(hf); % figure画像を取得。
[A, map] = rgb2ind(frame2im(frames), 256); % 画像形式変換
if n == 1
imwrite(A, map, filename, 'gif', 'DelayTime', delay, ...
'LoopCount',Inf);
% 表示はdelay秒間。1コマ目で繰返し再生回数の設定。
else
imwrite(A, map, filename, 'gif', 'DelayTime', delay, ...
'WriteMode', 'append');
% 2コマ目以降には、"追記"の指示が必要。
end
end
% 引き続き、無限ループで連続回転
disp('無限ループで実行中です。実行の停止は、Ctrl-C で。')
az=az0;
while true
az=az+azd;
if az>=180
az=az-360;
elseif az<-180
az=az+360;
end
ax1.View=[az el0];
ax2.View=[az el0];
drawnow;
pause(0.05); % 0.05秒の休止
end
% ===============================================
% ローカル関数
% ===============================================
function [hf,axA,axB] = make_2_axes()
% 1つの figure 内に横並びの2つの画面を作って、
% それぞれの axes いっぱいに赤枠を描く。
% まずは、作図の目安にするため、既定の axes のサイズを取得
hfx=figure(1);
hax=axes;
Pf=hfx.Position; Pa=hax.Position;
Wa=Pf(3)*Pa(3); % axes の既定の幅 [px]
Ha=Pf(4)*Pa(4); % axes の既定の高さ [px]
close(1); % 用済みの figure を削除
% 標準サイズより小さめの axes を準備
k=0.7; % axes の倍率
Wa=round(k*Wa); Ha=round(k*Ha); % 小さな axes の幅と高さ [px]
Mt=0.25; Mb=0.15; Ml=0.15; Mc=0.05; Mr=0.15;
% Wa,Ha の値をベースにした、figure 内の
% 上,下,左,中,右の margin。
% 中 margin とは axes 間の間隔のこと。
% 2つの axes を持った新しい figure を開く。
WT=2+Ml+Mc+Mr; % 新しい figure の幅と高さの見積もり
HT=1+Mt+Mb; % (Wa,Ha の値をベース)
hf=figure(1);
hf.Position=[100 50 Wa*WT Ha*HT]; % px 単位の figure の Position。
axA=axes('Position',[Ml/WT Mb/HT 1/WT 1/HT],'Color','w');
% 左側の axes の Position を設定
axB=axes('Position',[(Ml+1+Mc)/WT Mb/HT 1/WT 1/HT],'Color','w');
% 右側の axes の Position を設定
for n=[axA axB]
axes(n)
axis off
axis([0 1 0 1]);
hold on
plot([0 1 1 0 0],[0 0 1 1 0],'r','LineWidth',1); % 赤色の外枠
plot([0 1 NaN 0 1],[0 1 NaN 1 0],'Color','#aaa'); % 対角線
if n==axA
title('CameraViewAngle = auto にて、azimuth 角を漸増')
else
title('CameraViewAngle = 一定値 にて、azimuth 角を漸増')
end
end
end
2.4 CameraPosition と 再度 CameraViewAngle
縦画角の自動調整機能がオフのとき、観察対象の表示サイズを調整するためには、視点を近付けたり遠ざけたりする(CameraPosition)か、視点の位置はそのままでズームレンズで覗く(CameraViewAngle)か の2つの方法があります。後者の場合、画角が小さい望遠レンズでは観察対象が大きく見え、画角が大きい広角レンズでは小さく見えます。
図3が前者の方法を、図4が後者の方法を採用した場合の動作です。球体が小さめに見えるときには、両者の違いはあまり目立ちません。しかし、大きくなると違いがはっきりしてきます。CameraViewAngle を変えている図4では、画像が相似形のままで拡大縮小するだけです。それに対し、図3の CameraPosition を変えた場合には、球の表側と裏側の緯線の重なり具合が変化しているのが確認できます。したがって相似形にはなりません。これは日常の経験から考えても当然の現象です。
(注: 図3と図4の動きを同期させたい場合には、モニタ画面上に2つの図が同時に表示されている状態で、ブラウザの「ページ更新」ボタンをクリックしてください。)
図3 CameraPosition による遠近移動(CameraViewAngle: 左=auto / 右=一定値)
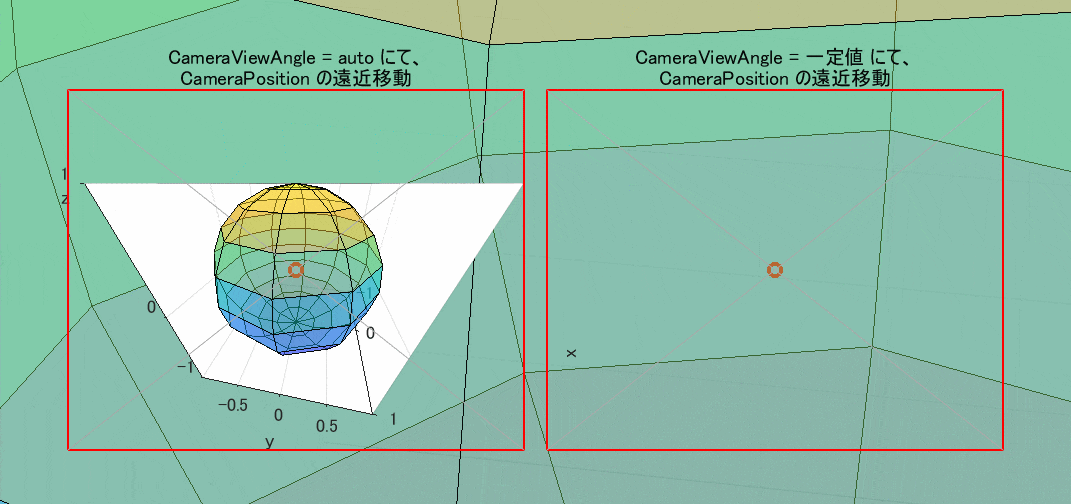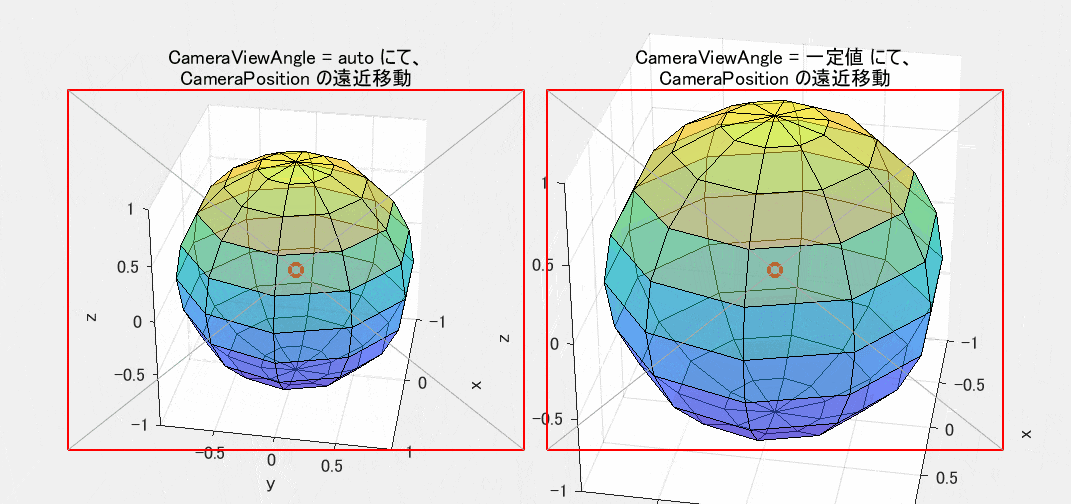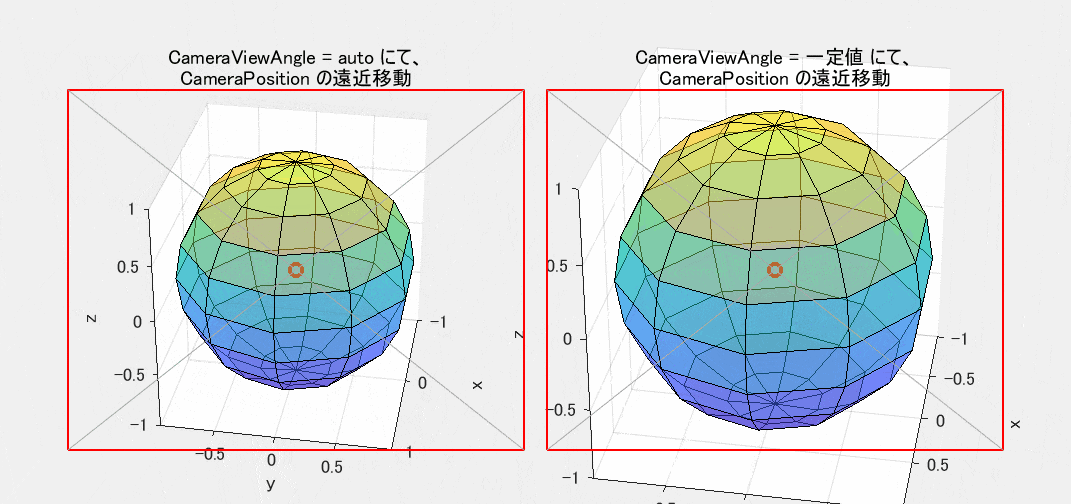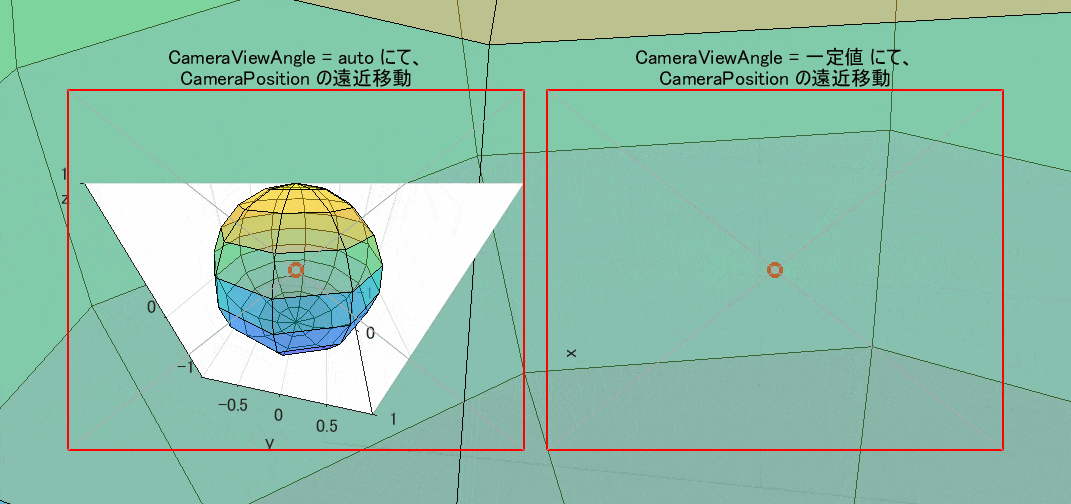
図4 CameraViewAngle による拡大縮小(左=一定値 / 右=増減)
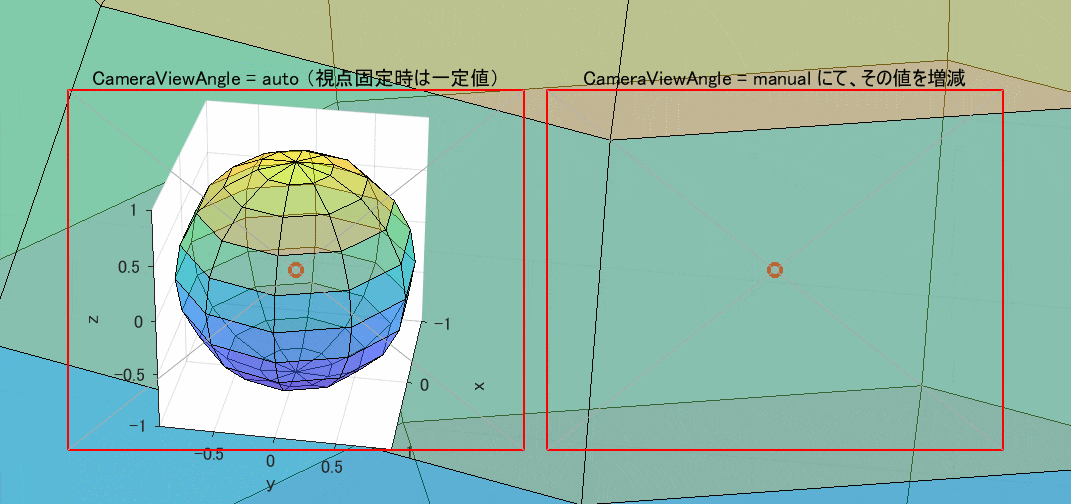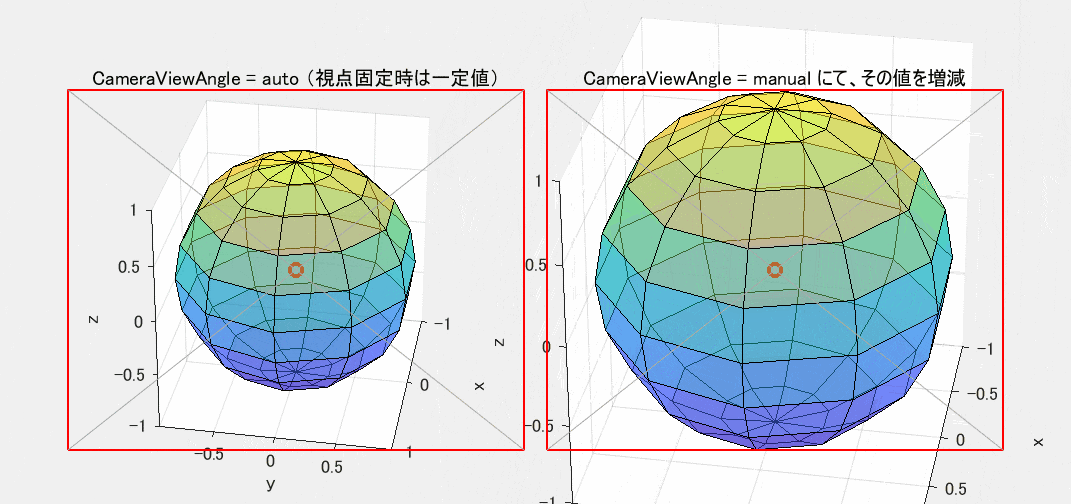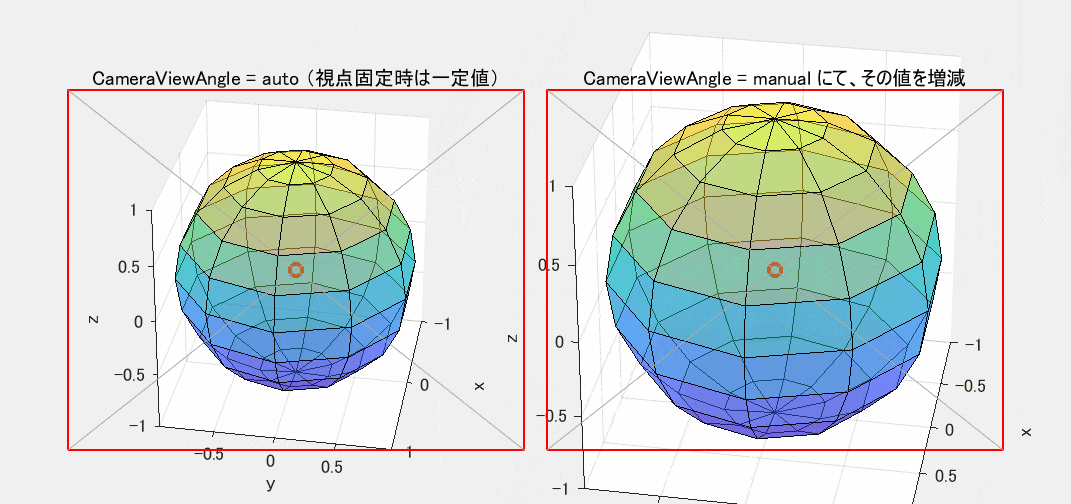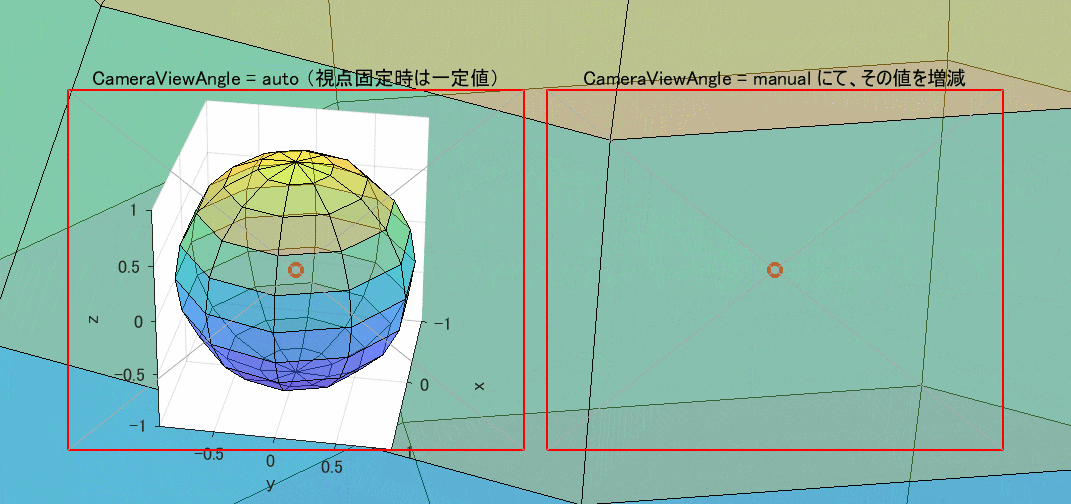
なお、図3,4とも Projection は perspective(透視投影)に設定しています。この設定を orthographic(正投影)に変えると、図3の方も画像が相似形のまま拡大縮小するだけになってしまいます(図示は省略)。orthographic は、観察対象からの遠近を問わず、常にそれを無限遠方から見たときと同じ形にするという便宜的な投影法です。現実の見え方と合わなくなるのは仕方がないことです。
それにしても、CameraViewAngleMode が manual のときには、その画角次第では、観察対象が無制限に拡大し、figure の全域までも埋め尽くすというド迫力には驚きます。
さて、一般に、一つの figure に二次元と三次元のグラフ(axes)を混在させると、三次元グラフだけが小さめに表示されて見劣りすることがあります。そんなときには、縦画角のこの性質を利用して、三次元グラフの CameraViewAngle を小さめに設定して図を拡大すると、バランスがとれた望ましい形に整えることができます。
図3,4用のプログラムは、他の図のプログラムとの類似部分が多いので掲載は割愛します。強いて特筆すべき点を挙げれば、拡大されたときの動きをじっくりと見られるように、時間ステップを非線形化しているところでしょうか。
2.5 CameraTarget
いままでは CameraTargetMode が既定の auto のままだったため、視線の先の点、言い換えれば赤枠の中心、さらには視野の中心をも意味する CameraTarget は【作図箱の中心点(赤〇印)】と一致していました。しかし、図5では、manual モードに切り替えて視野の中心位置を変化させています。青〇印が CameraTarget として新たに指定した点です。この点を【赤〇印を通り $y$ 軸に平行な緑色の線】の上で移動させています(この図では作図箱の中心を原点に置いているため、緑色の線は $y$ 軸そのものです)。
さて、CameraViewAngleMode の auto の効果はもう十分に理解できたと思いますが、ここでも左側にそのまま表示しています。しかし、ここでは、右側の CameraViewAngle を固定した図だけにご注目ください。
この動きはなかなか複雑です。自分が居る位置からは移動せずに、首を左右に傾げることなく、視線を上下左右に動かし(言い換えれば、頭を左右軸、上下軸周りだけで回転させ)ながら青〇印を追っているだけの状態です。しかし、直感による予想とは異なり、景色が相似形のまま単純に平行移動するわけではありません。説明は省きますが、道理に合わせてじっくりと考えてみれば、この動きが当然の結果であることは理解できると思います。なお、青〇印が赤〇印から大きく離れている状態では、肝心の観察対象を 網膜の片隅でしか見ていません。この状態での利用機会はそれほど多くはなさそうに思えます。
既述のように、右の図では CameraViewAngle を固定しています。それでも、図2の場合とは異なって、振れが大きな所では球体の大きさが少し変化し、しかも歪んでいるように見えます。これは、広角レンズで集合写真を撮ったとき、端の方の人だけが膨れて見えるのと同じようなもので、透視投影法の原理からみて当然の現象です。
図5 CameraTarget による視野の中心の移動(CameraViewAngle: 左=auto / 右=一定値)
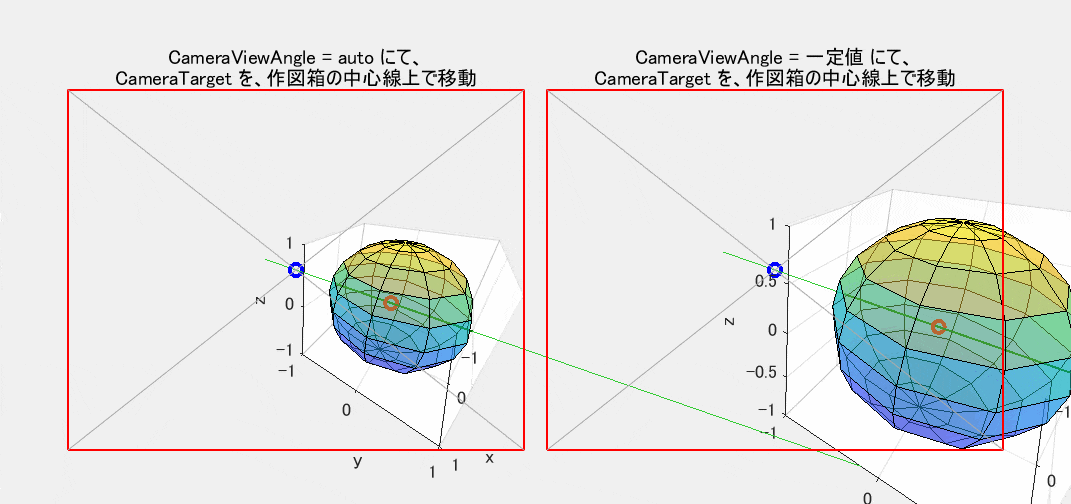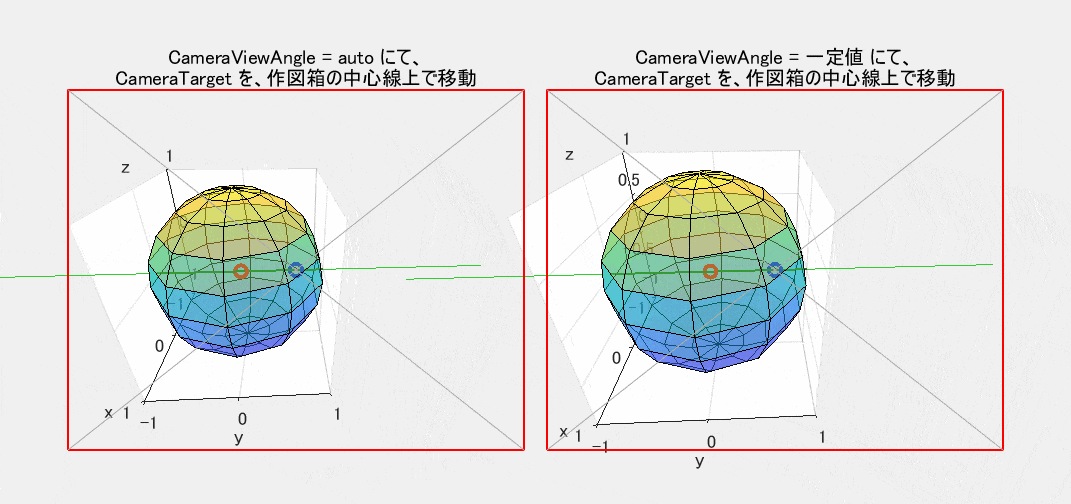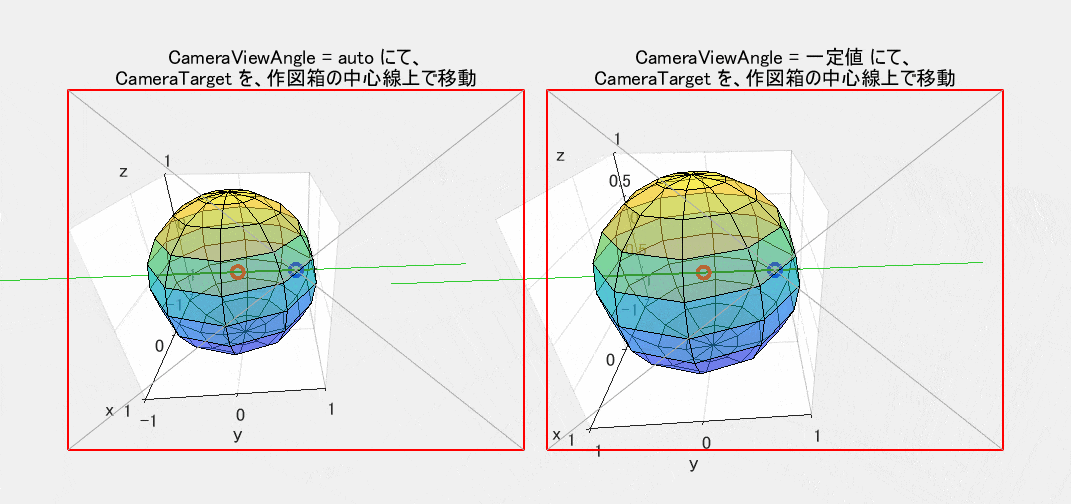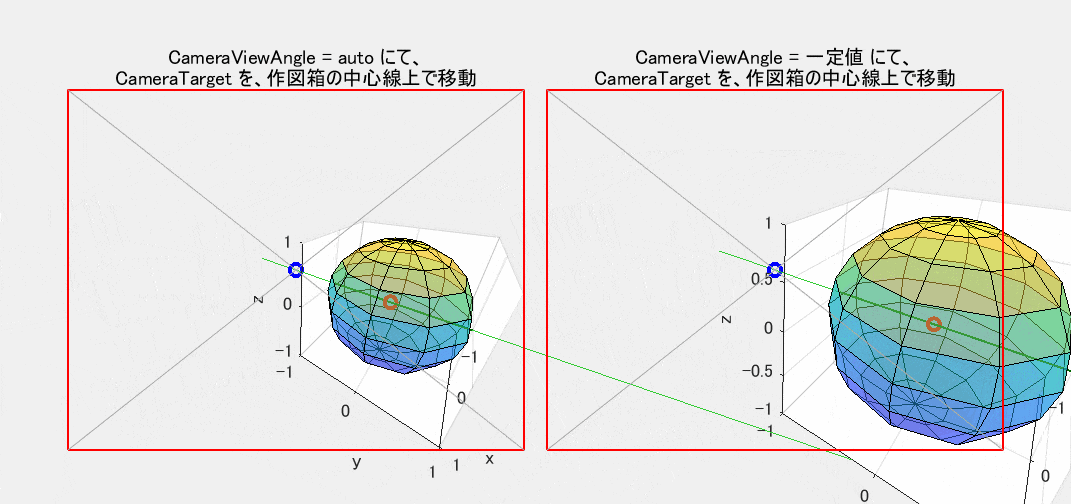
図5用のプログラムも、他の図のプログラムとの類似部分が多いので掲載は割愛します。
2.6 CameraUpVector
CameraUpVector を指定すると、【そのベクトルを、始点が CameraTarget と一致するように平行移動した状態での二次元投影像】が赤枠の真上を向くように、観察対象全体が CameraTarget を中心にして回転します。回転前後の図形は相似形です(CameraViewAngle が固定されていれば合同です)。図6は、図5のプログラムに、CameraUpVector として $y$ 軸方向の単位ベクトル [0 1 0] を指定した結果の動作です。図5では、CameraTarget を $y$ 軸上で動かしているので、ちょうどこの線が真上を向くように視野が回転します。なお、CameraUpVector を指定していない図5では、既定によって $z$ 軸方向の単位ベクトル [0 0 1] を指定したのと同様の動作になっています。
図6は、【図5の作図箱の緑色の中心線】が視野の真上を向くように、首の左右の傾きだけで調整(言い換えれば、頭を前後軸周りだけで回転)した場合と同じ形状になります。したがって、この動作は、単に、二次元図形を同一面内で回転しているに過ぎません。もし、回転だけが目的であれば、わざわざ三次元ベクトルを使ってまで操作する必要はありません。1つのスカラー量だけで十分です。関連コマンドの camroll($\varphi$) を使えば、三次元図を、視線(視点→視野の中心)を軸にして、反時計回りに $\varphi$ 度だけ回転することができます。なお、このコマンド名に直結するプロパティはありませんが、間接的に CameraUpVector プロパティを使っているものと思われます。
図6 図5に CameraUpVector を指定(CameraViewAngle: 左=auto / 右=一定値)
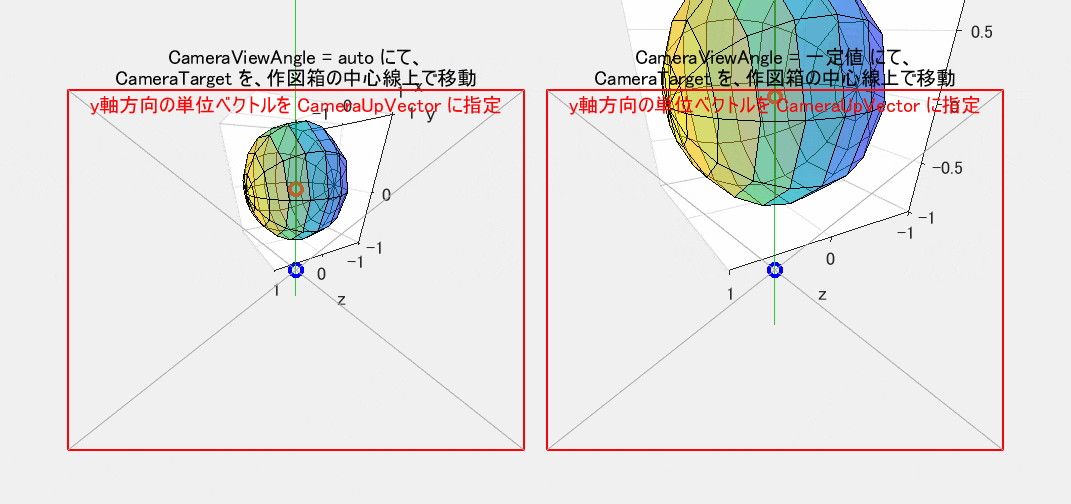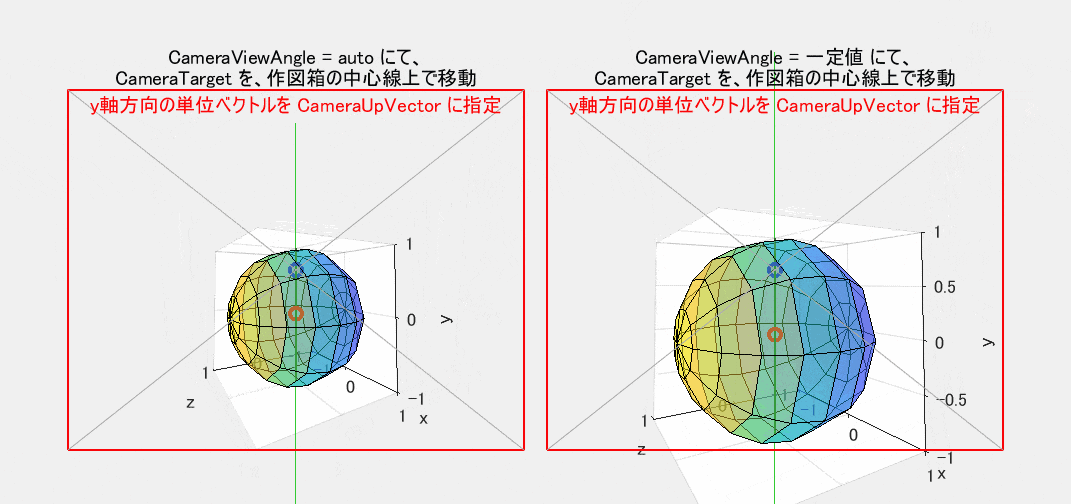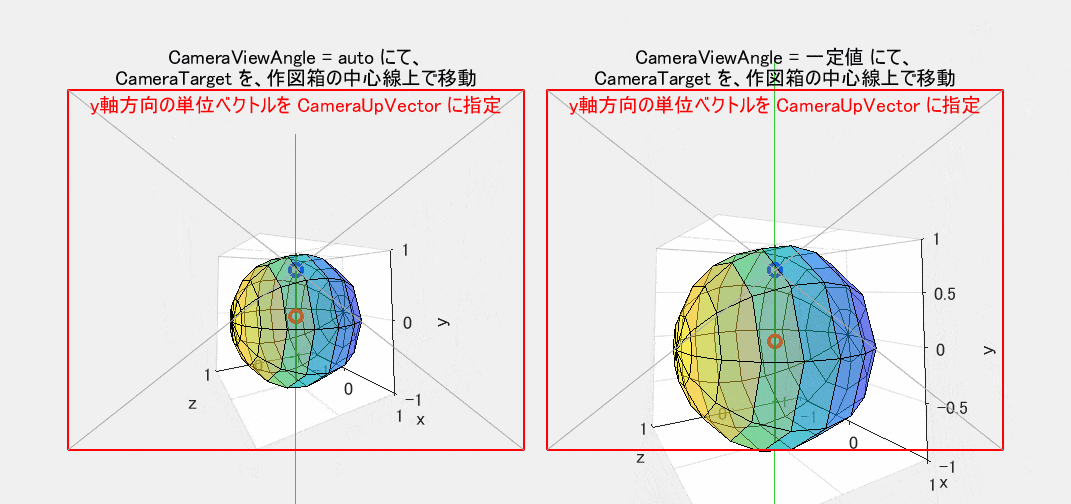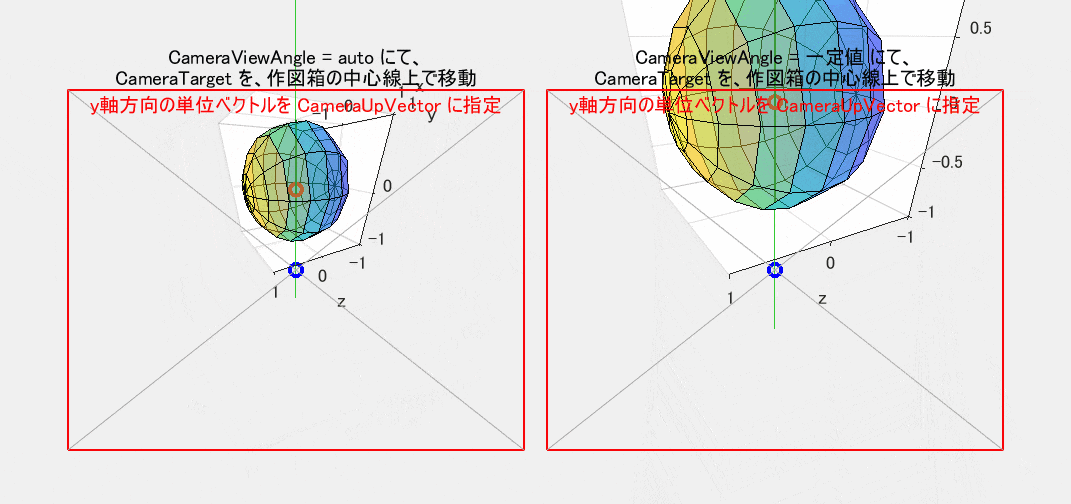
図6用のプログラムも、他の図のプログラムとの類似部分が多いので割愛します。
3.応用
ここでは、RICOH THETA などで撮影した全方位画像を、MATLAB を使って鑑賞する例を紹介します。三次元プロットで作図した普通の球殻の外側に、図7に示した原画像を裏返しにして貼り付けます。そして、この球殻の内側に入って CameraPosition や CameraViewAngle を操作しながら動き回ると、図8のような動画を作ることができます。Projection は perspective にし、CameraTarget は常に球殻の中心に置いています。
一見、閉所恐怖に襲われそうな場面設定ですが、ご心配は無用です。予想に反し、広大な宇宙から地球を眺めているような開放的な感覚に浸ることができます。一応はうまく動作しているように見えますが、天頂や足元が画面の中心に来るようなとき、画像の微妙な位置の調整が困難です。そのため、芸術的な拘りは諦めて適当なところで妥協しています。CameraTarget の調整で画像の位置は動かせますが、画像全体の予期しない回転も伴うのでなかなか難しいところです。まだまだ改良・検討の余地がありそうです。
プログラム
図8を描画するプログラムを次に示します。
ここをクリックしてプログラムを開/閉
% view_point30.m
% 平和祈念像の静止画の全方位写真からアニメ gif 動画を作成する。
% ① 見せ場のシーンを4つ決めて、 それぞれの figure を作成する。
% ② 各シーンでの視点関連プロパティも記録しておく。
% ③ それらのシーンの間を、プロパティを補間しながら移動する。
% (動画のサイズを低減するために、MATLAB 画面は小さくする)
clear
close all
% 平和祈念像の全方位写真画像の取り込み
A=imread('peace_park01.jpg'); % 変数 A に画像を取り込む
A=flipud(A); % 上下反転(MATLAB の画像処理事情より)
A=fliplr(A); % 左右反転(裏から見て正像となるように)
[X,Y,Z]=sphere(30); % 球殻のデータを生成(半径は 1.0)
Ptgt=[0 0 0]; % 視線の先は、常に球殻の中心
% 未加工のオリジナル三次元球面画像の作成
figure(1)
s = surf(X,Y,Z); % 球殻を描く
hold on
axis equal
s.FaceColor = 'texturemap'; % 球殻表面に
s.CData = A; % 画像を貼り付ける。
s.EdgeColor = 'none'; % 球殻のメッシュ線を削除
ax=gca;
h1=get(ax,'Children'); % 未加工のオリジナル三次元球面画像を
% 再利用のために h1 にコピーしておく。
% ======================
% 見せ場シーン1
% 平和祈念像の寄り画像
% ======================
% このシーンのプロパティ
Lcam=0.1; az=-205; el=-27; va=26;
% Lcam: 球の中心から視点までの距離(半径は 1.0)
% az: 球の中心から視点までの水平角度 [度]
% az 増で、天頂から見て反時計回り
% el: 球の中心から視点までの垂直角度 [度]
% 地表から天頂に向かう方向が +
% va: 縦視角 [度]
Scn(1,:)=[Lcam az el va]; % シーン配列の1行目として記録
% 見せ場シーン吟味用の figure にプロパティを適用
x=Lcam*cosd(el)*cosd(az); y=Lcam*cosd(el)*sind(az); z=Lcam*sind(el);
ax.CameraPosition=[x y z]; % 視点の座標
ax.CameraViewAngle=va; % 視角
ax.CameraTarget=Ptgt; % 視線の先の座標
ax.Projection='perspective'; % 透視図法
% ======================
% 見せ場シーン2
% 平和祈念像の引き画像
% ======================
% このシーンのプロパティ
Lcam=0.1; az=-205; el=0; va=80;
Scn(2,:)=[Lcam az el va]; % シーン配列の2行目として記録
figure(2)
axes;
ax=gca;
copyobj(h1,ax); % 未加工のオリジナル球面画像を貼り付け
axis equal
% 見せ場シーン吟味用の figure にプロパティを適用
x=Lcam*cosd(el)*cosd(az); y=Lcam*cosd(el)*sind(az); z=Lcam*sind(el);
ax.CameraPosition=[x y z];
ax.CameraViewAngle=va;
ax.CameraTarget=Ptgt;
ax.Projection='perspective';
% ======================
% 見せ場シーン3
% 天頂中心の超広角画像
% ======================
% このシーンのプロパティ
Lcam=1; az=-200; el=-89; va=85;
Scn(3,:)=[Lcam az el va]; % シーン配列の3行目として記録
figure(3)
axes;
ax=gca;
copyobj(h1,ax); % 未加工のオリジナル球面画像を貼り付け
axis equal
% 見せ場シーン吟味用の figure にプロパティを適用
x=Lcam*cosd(el)*cosd(az); y=Lcam*cosd(el)*sind(az); z=Lcam*sind(el);
ax.CameraPosition=[x y z];
ax.CameraViewAngle=va;
ax.CameraTarget=Ptgt;
ax.Projection='perspective';
% ======================
% 見せ場シーン4
% 足元中心の超広角画像
% ======================
% このシーンのプロパティ
Lcam=1; az=-200; el=89; va=125;
Scn(4,:)=[Lcam az el va]; % シーン配列の4行目として記録
figure(4)
axes;
ax=gca;
copyobj(h1,ax); % 未加工のオリジナル球面画像を貼り付け
axis equal
% 見せ場シーン吟味用の figure にプロパティを適用
x=Lcam*cosd(el)*cosd(az); y=Lcam*cosd(el)*sind(az); z=Lcam*sind(el);
ax.CameraPosition=[x y z];
ax.CameraViewAngle=va;
ax.CameraTarget=Ptgt;
ax.Projection='perspective';
% ===============================
% アニメ gif の繰り返し動画を作成
% ===============================
hf=figure(5);
% アニメ gif の容量削減のため figure のサイズを小さくする。
hP=hf.Position;
hf.Position=[hP(1) hP(2) hP(3)*0.45 hP(4)*0.45];
axes;
ax=gca;
copyobj(h1,ax); % 未加工のオリジナル球面画像を貼り付け
axis equal
ax.CameraTarget=Ptgt;
ax.Projection='perspective';
% ===== 動画のファイル名 =====
filename = 'view_point30.gif'; % 動画のファイル名
delay=1/24; % 一コマの秒数(24コマ/秒)
Nf=0; % 全カット通しでのコマ番号
% ======================================================
% 【見せ場シーン1】から【見せ場シーン2】への移行カット
% ======================================================
nf=30; % このカットで使用するコマ数
% 開始・終了シーンのプロパティと、1コマ当たりの差分
Scn0=Scn(1,:); Scn1=Scn(2,:); dScn=(Scn1-Scn0)/nf;
Sc=Scn0; % ブロパティに初期値を設定
for n=1:nf+1
Nf=Nf+1;
Lcam=Sc(1); az=Sc(2); el=Sc(3); va=Sc(4); % プロパティ値の更新
x=Lcam*cosd(el)*cosd(az); y=Lcam*cosd(el)*sind(az); z=Lcam*sind(el);
ax.CameraPosition=[x y z];
ax.CameraViewAngle=va;
drawnow;
if n==1 | n==nf+1
delayT=1.0;
else
delayT=delay;
end
frames=getframe(hf); % figure画像を取得。
[B, map] = rgb2ind(frame2im(frames), 256); % 画像形式変換
if n == 1
imwrite(B, map, filename, 'gif', 'DelayTime', delayT, ...
'LoopCount',Inf);
% 表示はdelay秒間。1コマ目で繰返し再生回数の設定。
else
imwrite(B, map, filename, 'gif', 'DelayTime', delayT, ...
'WriteMode', 'append');
% 2コマ目以降には、"追記"の指示が必要。
end
Sc=Sc+dScn; % プロパティ値を1コマ分だけ変化
end
% ======================================================
% 【見せ場シーン2】から、周囲を一回りして元に戻るカット
% ======================================================
nf=20; % このカットで使用するコマ数
Scn0=Scn(2,:); Scn1=[Scn(2,1) Scn(2,2)+360 Scn(2,[3 4])];
dScn=(Scn1-Scn0)/nf;
Sc=Scn0; % ブロパティに初期値を設定
for n=1:nf+1
Nf=Nf+1;
Lcam=Sc(1); az=Sc(2); el=Sc(3); va=Sc(4); % プロパティ値の更新
x=Lcam*cosd(el)*cosd(az); y=Lcam*cosd(el)*sind(az); z=Lcam*sind(el);
ax.CameraPosition=[x y z];
ax.CameraViewAngle=va;
drawnow;
if n==nf+1
delayT=1.0;
else
delayT=delay;
end
frames=getframe(hf); % figure画像を取得。
[B, map] = rgb2ind(frame2im(frames), 256); % 画像形式変換
imwrite(B, map, filename, 'gif', 'DelayTime', delayT, ...
'WriteMode', 'append');
Sc=Sc+dScn; % プロパティ値を1コマ分だけ変化
end
% ======================================================
% 【見せ場シーン2】から【見せ場シーン3】への移行カット
% ======================================================
nf=30; % このカットで使用するコマ数
% 開始・終了シーンのプロパティと、1コマ当たりの差分
Scn0=Scn(2,:); Scn1=Scn(3,:); dScn=(Scn1-Scn0)/nf;
Sc=Scn0; % ブロパティに初期値を設定
for n=1:nf+1
Nf=Nf+1;
Lcam=Sc(1); az=Sc(2); el=Sc(3); va=Sc(4); % プロパティ値の更新
x=Lcam*cosd(el)*cosd(az); y=Lcam*cosd(el)*sind(az); z=Lcam*sind(el);
ax.CameraPosition=[x y z];
ax.CameraViewAngle=va;
drawnow;
if n==nf+1
delayT=1.0;
else
delayT=delay;
end
frames=getframe(hf); % figure画像を取得。
[B, map] = rgb2ind(frame2im(frames), 256); % 画像形式変換
imwrite(B, map, filename, 'gif', 'DelayTime', delayT, ...
'WriteMode', 'append');
Sc=Sc+dScn; % プロパティ値を1コマ分だけ変化
end
% ======================================================
% 【見せ場シーン3】から【見せ場シーン4】への移行カット
% ======================================================
nf=40; % このカットで使用するコマ数
% 開始・終了シーンのプロパティと、1コマ当たりの差分
Scn0=Scn(3,:); Scn1=Scn(4,:); dScn=(Scn1-Scn0)/nf;
Sc=Scn0; % ブロパティに初期値を設定
for n=1:nf+1
Nf=Nf+1;
Lcam=Sc(1); az=Sc(2); el=Sc(3); va=Sc(4); % プロパティ値の更新
x=Lcam*cosd(el)*cosd(az); y=Lcam*cosd(el)*sind(az); z=Lcam*sind(el);
ax.CameraPosition=[x y z];
ax.CameraViewAngle=va;
drawnow;
if n==nf+1
delayT=1.0;
else
delayT=delay;
end
frames=getframe(hf); % figure画像を取得。
[B, map] = rgb2ind(frame2im(frames), 256); % 画像形式変換
imwrite(B, map, filename, 'gif', 'DelayTime', delayT, ...
'WriteMode', 'append');
Sc=Sc+dScn; % プロパティ値を1コマ分だけ変化
end
4.定量的な解釈
4.1 諸量や用語の図解
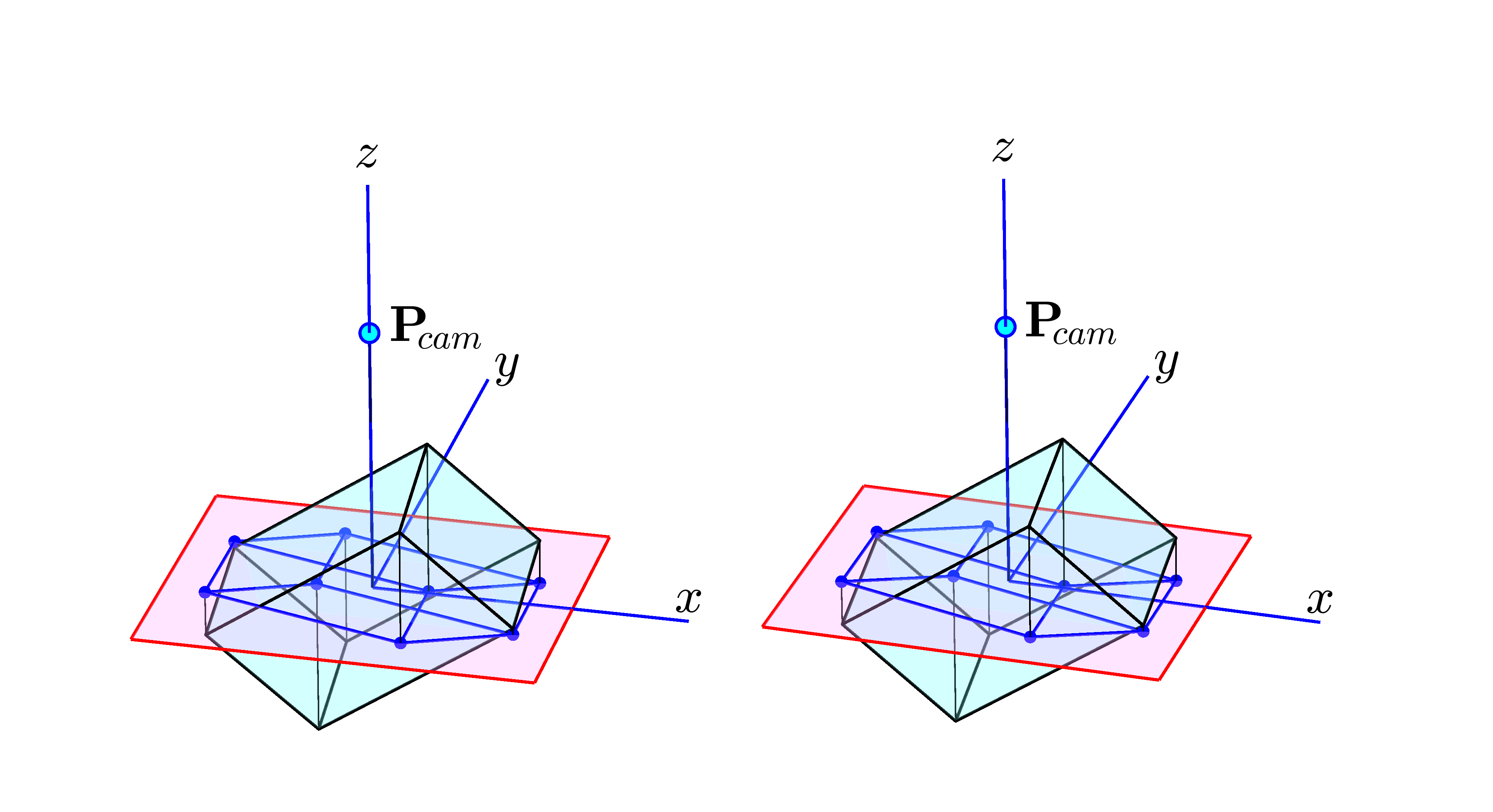
数式ばかりを使って説明するのでは、書く側も読む側も疲れます。図解で分かるものはそれで済まそうと思います。しかし、二次元の図を使って三次元のモデルを示そうとすると、多くの線が込み入って勘違いが多くなりそうです。そこで、できるだけ、裸眼立体視による三次元図を利用してみようと思います。左右の画像間の距離が 60~65 [mm] 程度になるようにブラウザの画面の大きさを調整してから閲覧してください。この条件を満たせない状態で見ようとすると、気分が悪くなることがあります。なお、これらの図は平行法での使用を前提としています。左の図は左目で、右の図は右目で見てください。
さて、観察対象を第3象限と第4象限の境界付近から眺めれば、$x$ 軸は右向き、$y$ 軸は上向きの見慣れた表現になります。しかし、図が複雑になる傾向があるので、やむなく、第1象限の上部から見下ろした図を描くことにしました。$x, y$ 軸の正/負の方向について見誤りやすいのでご注意ください。
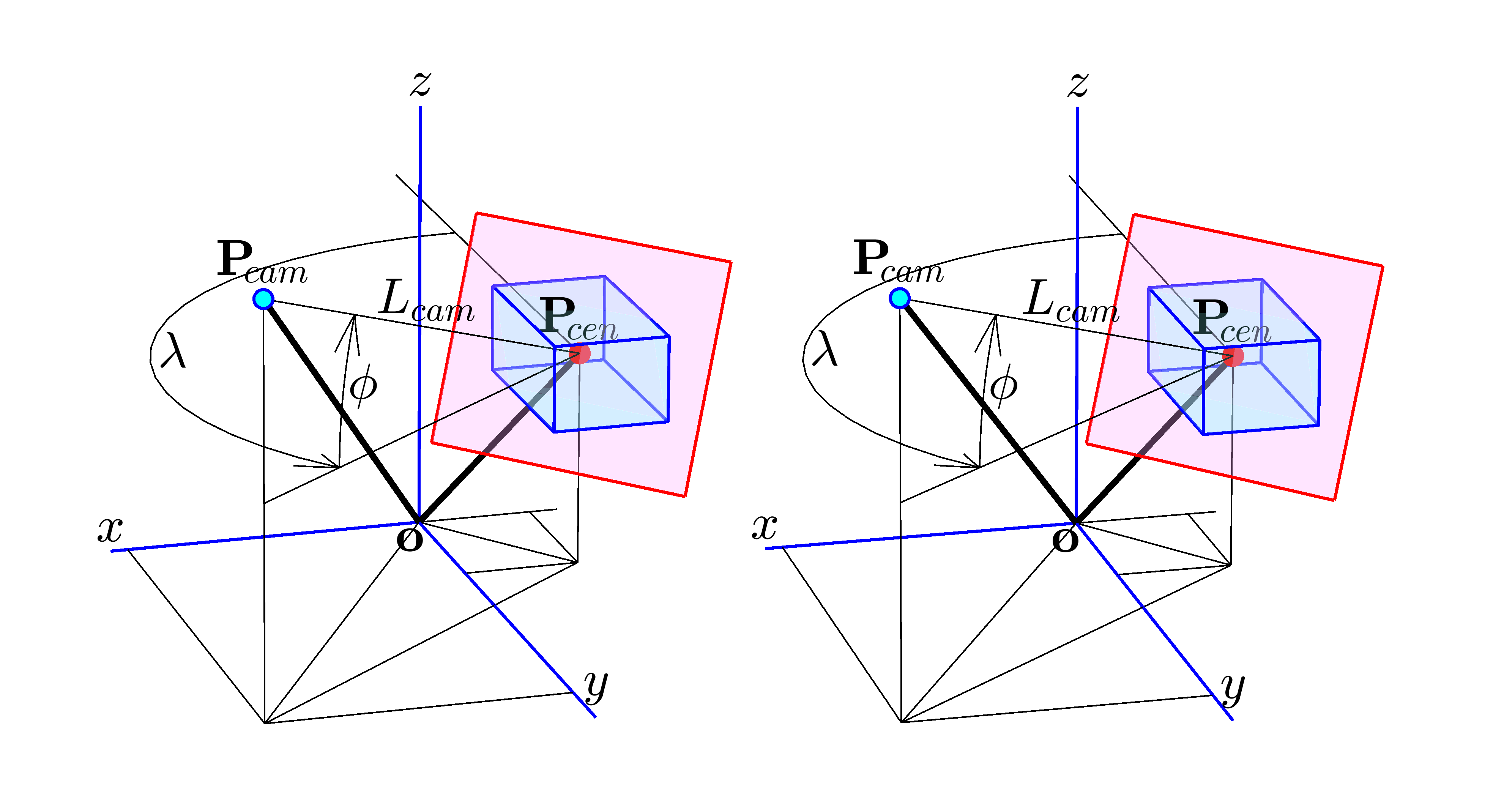
図9は観察系全体を示す基本図です。前掲の図2~6では、簡潔さを重視して、作図箱の中心を原点 $\mathbf{o}$ と一致させていました。しかし、図9は、より一般的な説明にも使えるように、これらの点を分離して配置させたものです。右手系の直交座標上に水色の作図箱が置かれています。その中心点は $\mathbf{P}_{\!cen}$ というベクトルで表しています。この点と中心を共有し、赤く縁取りされたピンク色の平面が配置されています。この赤い縁取りが前述の赤枠に対応しています。両者とも似たようなものですが、ここでは混同を避けるために仮想赤枠と呼ぶことにします。
$\mathbf{P}_{\!cam}$ は視点(CameraPosition)の座標値を表すベクトルです。視点の位置は、View の要素である方位角 (azimuth) $\lambda$ と仰角 (elevation) $\phi$ でも、やんわりと指定することはできます(ただし、長さ $L_{cam}$ は MATLAB が自動的に決めます)。方位角 $\lambda$ の基準線は $\mathbf{P}_{\!cen}$ を通り $y$ 軸の負側に平行に伸びた直線です。この $\lambda$ の正方向は、$z$ 軸の正側から見て反時計回りです。 また、仰角 $\phi$ は、$xy$ 平面と逆視線( $\mathbf{P}_{\!cam}{-}\mathbf{P}_{\!cen}$ )との角度差で表し、$z$ 軸の正側への逆視線が正の値になります。
図中の $L_{cam}$ は、二つの点 $\mathbf{P}_{\!cen}$ と $\mathbf{P}_{\!cam}$ の間の長さを示す量です。これは従属的に導かれるもので、独立したプロパティではありませんが、今後も多用される重要なパラメータです。なお、この立体視図からでは詳細には読み取れませんが、赤枠を含むピンク色の面は常に視線 $\mathbf{P}_{\!cen}{-}\mathbf{P}_{\!cam}$ と直交しており、赤枠の上辺と下辺は常に $xy$ 平面と平行になっています。
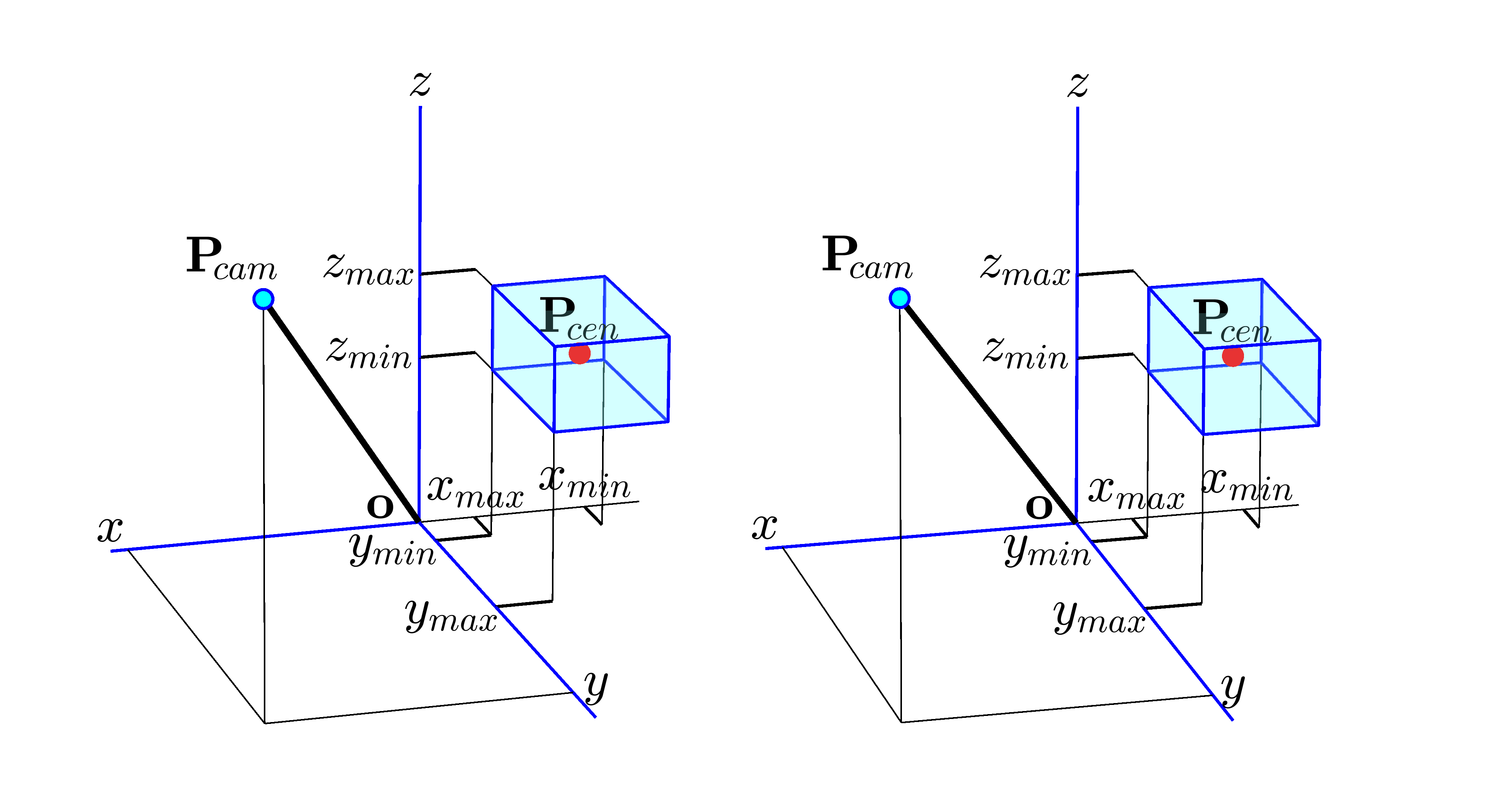
図示するまでもなさそうですが、作図箱の位置や大きさを示すパラメータ $x_{min}$, $x_{max}$, $y_{min}$, $y_{max}$, $z_{min}$, $z_{max}$ については図10に示すとおりです。
仮想赤枠は、スクリーン面に表示される二次元 axes の座標枠(赤枠)に対応するものです。しかし、axes を開いただけの段階では、この仮想赤枠の大きさはまだ定まりません。決まっているのは枠のアスペクト比(幅/高さ)$K_{asp}$ だけです。この値は例えば下記のようにして求められます。
hf=gcf; ha=gca; % figure と axes のハンドル
% アスペクト比
Kasp=hf.Position(3)*ha.Position(3)/(hf.Position(4)*ha.Position(4));
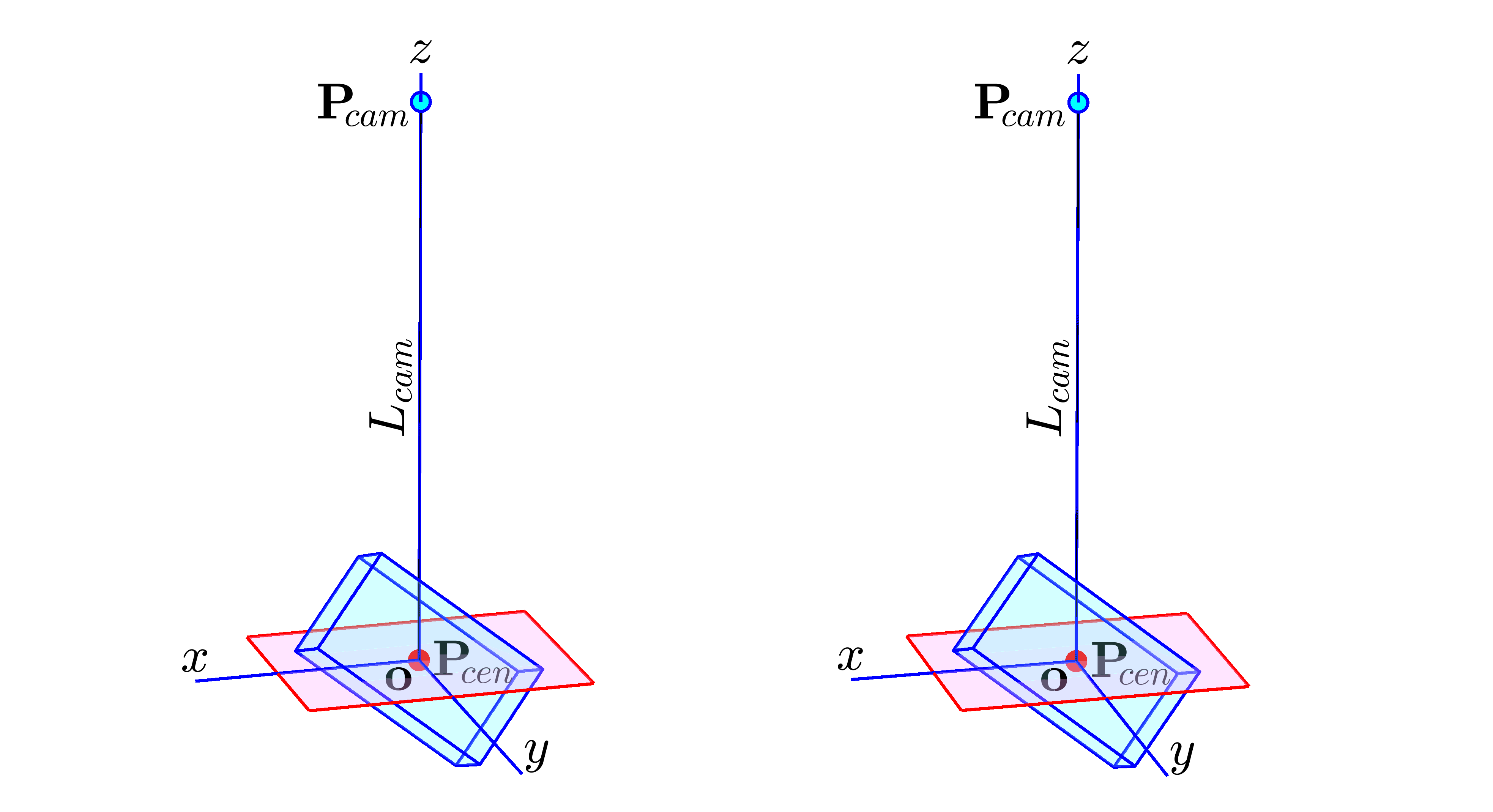
これに加えて $L_{cam}$ と CameraViewAngle $\theta$ が与えられると、仮想赤枠の大きさは次のようにして決まります。(図11参照)
$$
\begin{align}
&H_r=2L_{cam}\tan(\theta/2)\tag{1}\\
&W_r=K_{asp}H_r\tag{2}
\end{align}
$$
図11 縦画角 CameraViewAngle $\theta$ の定義
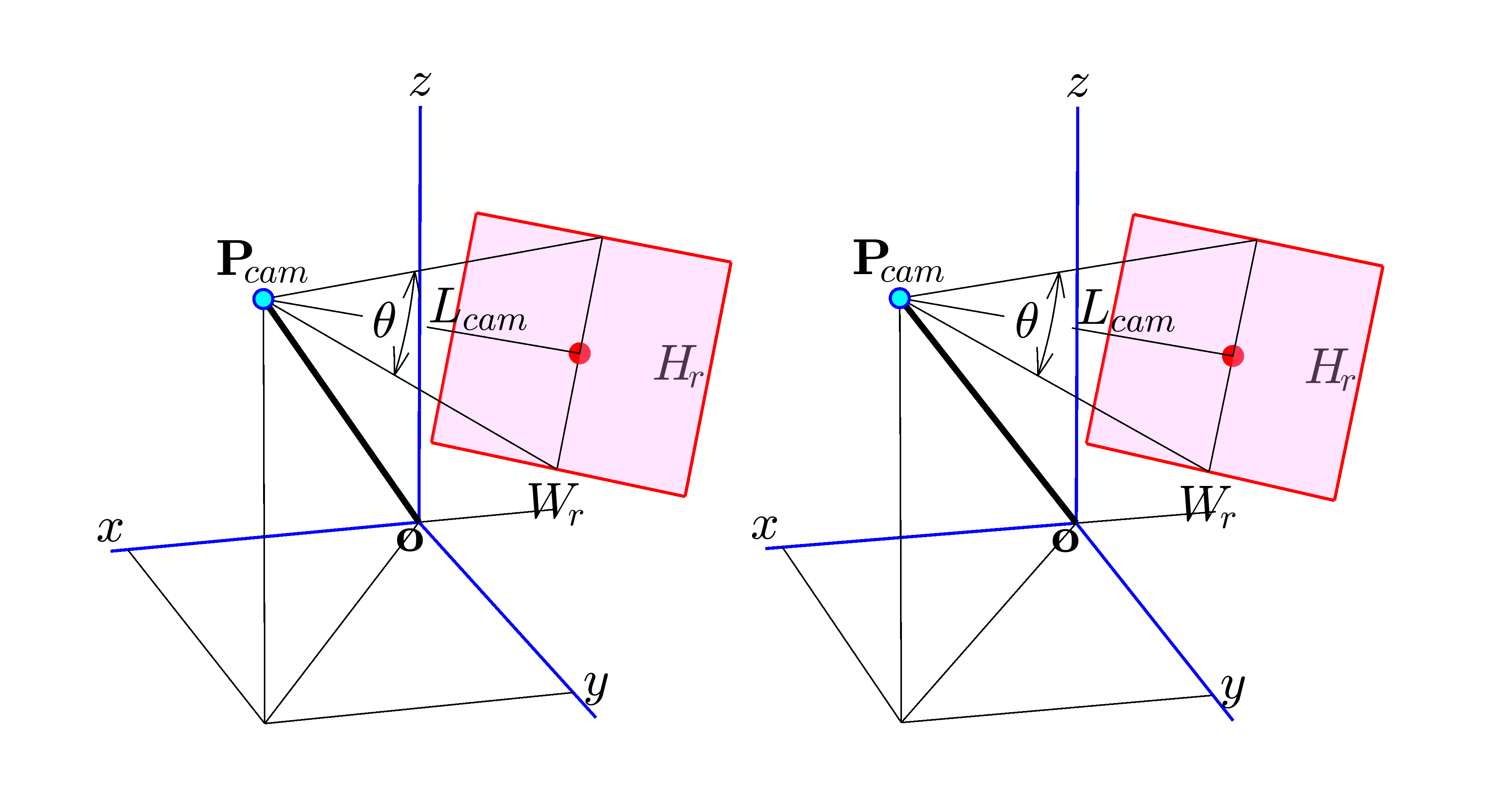
最終的には、仮想赤枠面(その延長面も含む)に投影(図15,16)された図形が、【この仮想赤枠とスクリーン上の赤枠とがピッタリと重なり合うように】相似的に拡大縮小されて axes 面に貼り付けられます。もし、仮想赤枠の外側にも投影図形が存在すれば、それらも排除されることなく、axes の外側にそのまま貼り付けられます。ただし、CameraViewAngleMode が auto の場合には、すべての観察対象が仮想赤枠内にきれいに収まるように、枠が自動的に伸縮する(CameraViewAngle が自動調整される)ため、観察対象の投影図形が axes 外にまで溢れ出すことはありません。
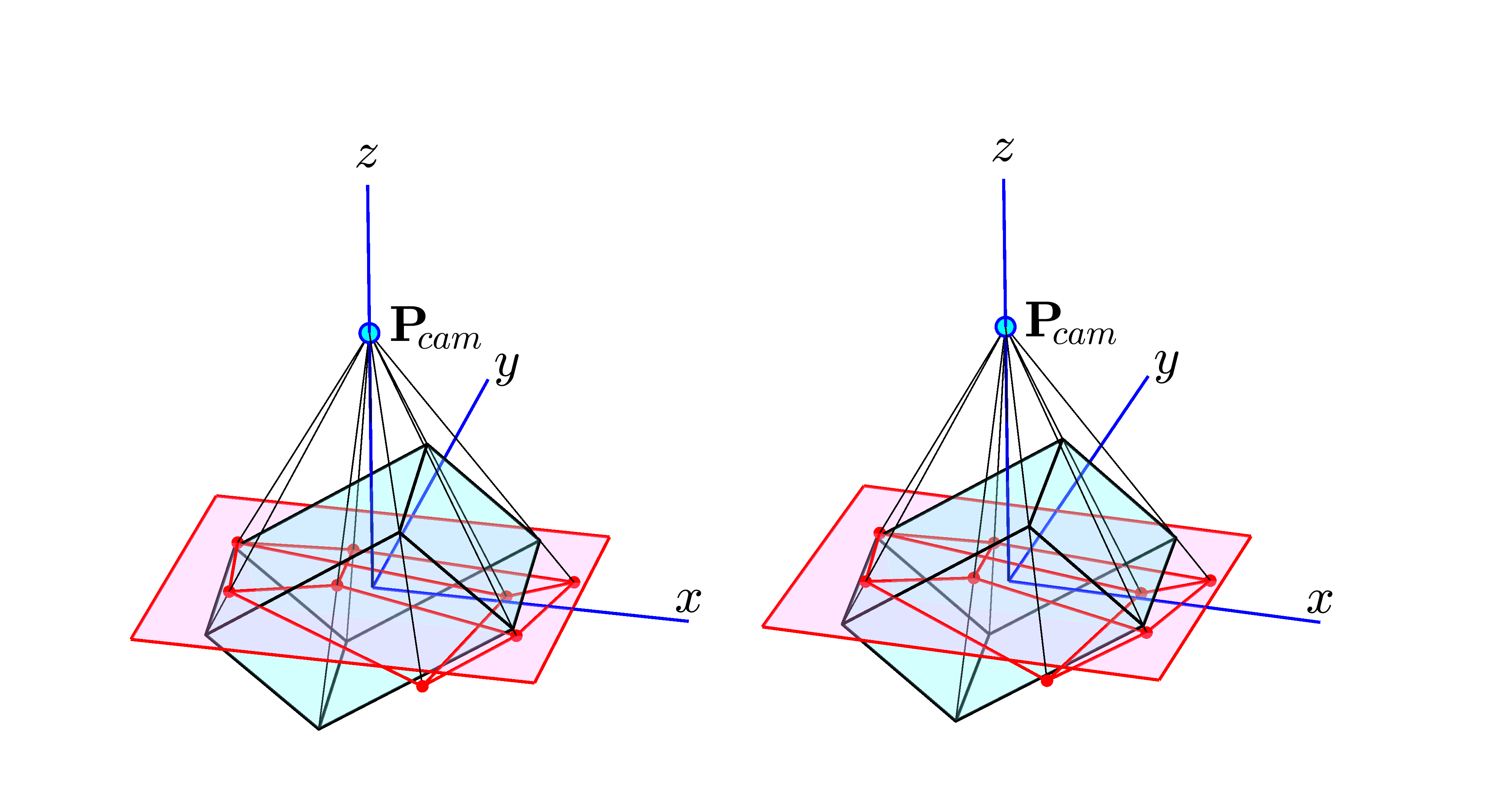
図9だけでは、CameraTarget の説明にはまだ不十分です。既定では、CameraTargetMode は auto なので、CameraTarget $\mathbf{P}_{\!tgt}$ は作図箱の中心 $\mathbf{P}_{\!cen}$ と一致しています。しかし、manual モードにすれば別の位置に設定することもできます。図12は、この状態をも考慮して一般化した観察系の構成です。
図12 CameraTarget $\mathbf{P}_{\!tgt}$ を任意の位置に移動した状態
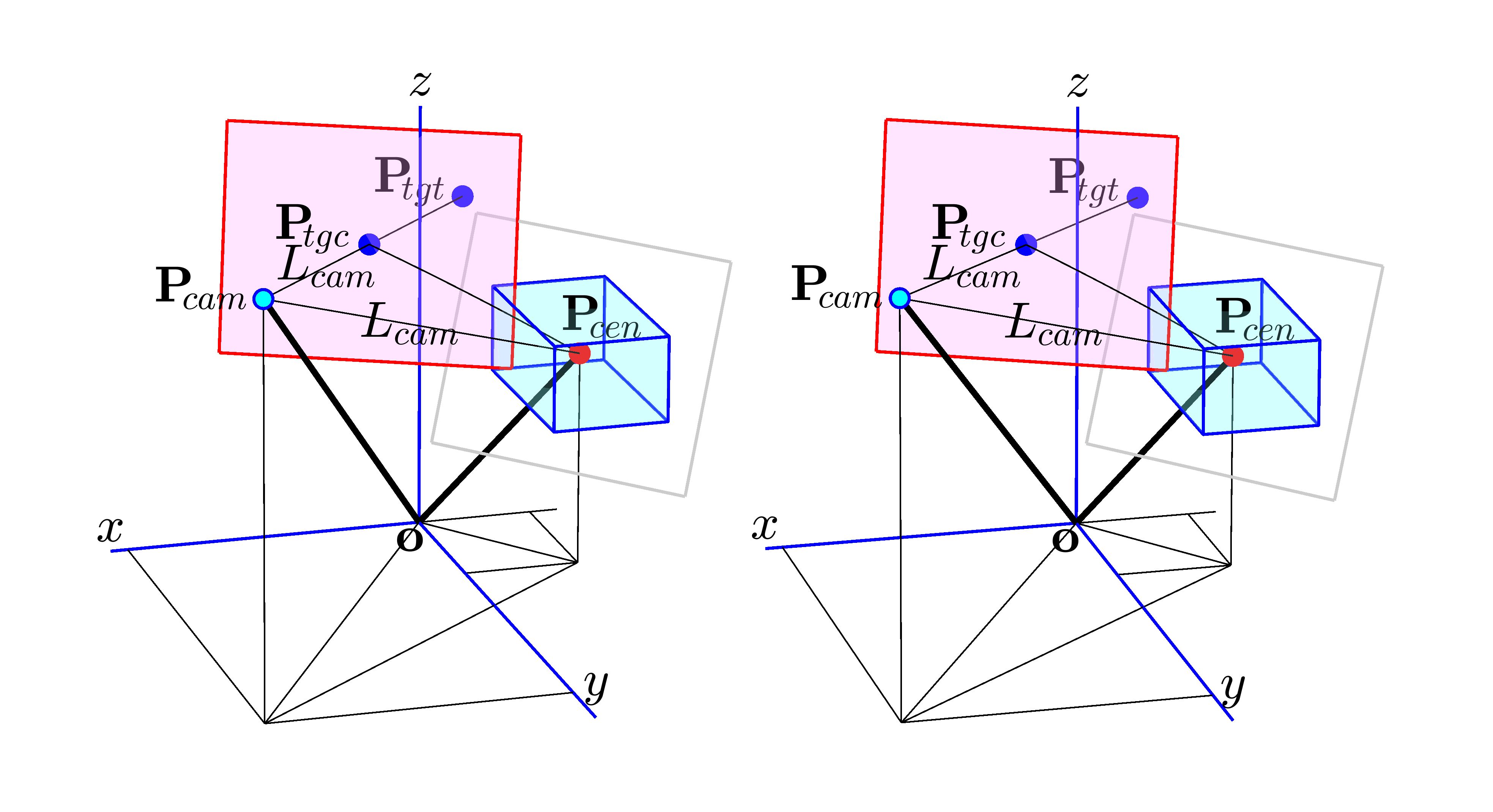
図中の $\mathbf{P}_{\!tgt}$ は、プロパティとして直接指定した CameraTarget の座標です。しかし、ここで重要になるのは、この $\mathbf{P}_{\!tgt}$ よりも、これと $\mathbf{P}_{\!cam}$ を結ぶ直線上にある、$\mathbf{P}_{\!cam}$ から $L_{cam}$ だけ離れた点 $\mathbf{P}_{\!tgc}$ です。図9では $\mathbf{P}_{\!cen}$ と重なっていたため特に命名はしていませんでしたが、ここではこの点 $\mathbf{P}_{\!tgc}$ を仮想赤枠中心と呼ぶことにします。新しい仮想赤枠の面は、$\mathbf{P}_{\!tgc}$ を中心にして、新しい視線 $\mathbf{P}_{\!tgc}{-}\mathbf{P}_{\!cam}$ と直交して配置されます。赤枠の大きさや、上辺と下辺の $xy$ 面との平行性は図9と同じように保たれています。
4.2 描画アルゴリズムの推定
4.2.1 不足している情報
これまで図示してきた諸量の関係を数式化すれば、MATLAB による三次元プロットは自己流でも再現できそうに思えます。しかし、実は、まだ解決しなければならない未知の部分が残っていました。それは次の2点です。
- View プロパティでは $L_{cam}$ を指定できません。MATLAB が自動的に見繕って決めているようですが、その決め方が分かりません。
- CameraTarget を指定し、Projection を正投影法にしたとき、MATLAB は、既出の図だけからは説明できないような三次元プロットを出力します。
これらの問題の解決には途方もない時間と労力が必要でした。苦労話を長々と披露したいところですが、読む人には迷惑でしかありません。気前よく結論だけを書くことにします。
View で方位角と仰角を指定したとき、$L_{cam}$ の値は次のようにして決まります。つまり、作図箱の対角線の5倍に相当する長さになります。なお、$L_x{=}x_{max}{-}x_{min}$、$L_y{=}y_{max}{-}y_{min}$、$L_z{=}z_{max}{-}z_{min}$ としています。
$$
L_{cam}=5\sqrt{{L_x}^2+{L_y}^2+{L_z}^2}\tag{3}
$$
また、正投影法で CameraTarget を指定したときだけは、特殊な投影方法が採用されており、次のようなステップを踏んでいるようです。それなりの採用理由はありそうですが、なかなか思い当たりません。
- まずは、本来の $\mathbf{P}_{\!tgc}$ を中心にした仮想赤枠面ではなく、これと平行で $\mathbf{P}_{\!tgt}$ を中心にした平面に「正投影」します。
- その投影された平面画像を、さらに本来の仮想赤枠面に「透視投影」します。
4.2.2 推定アルゴリズムの検証
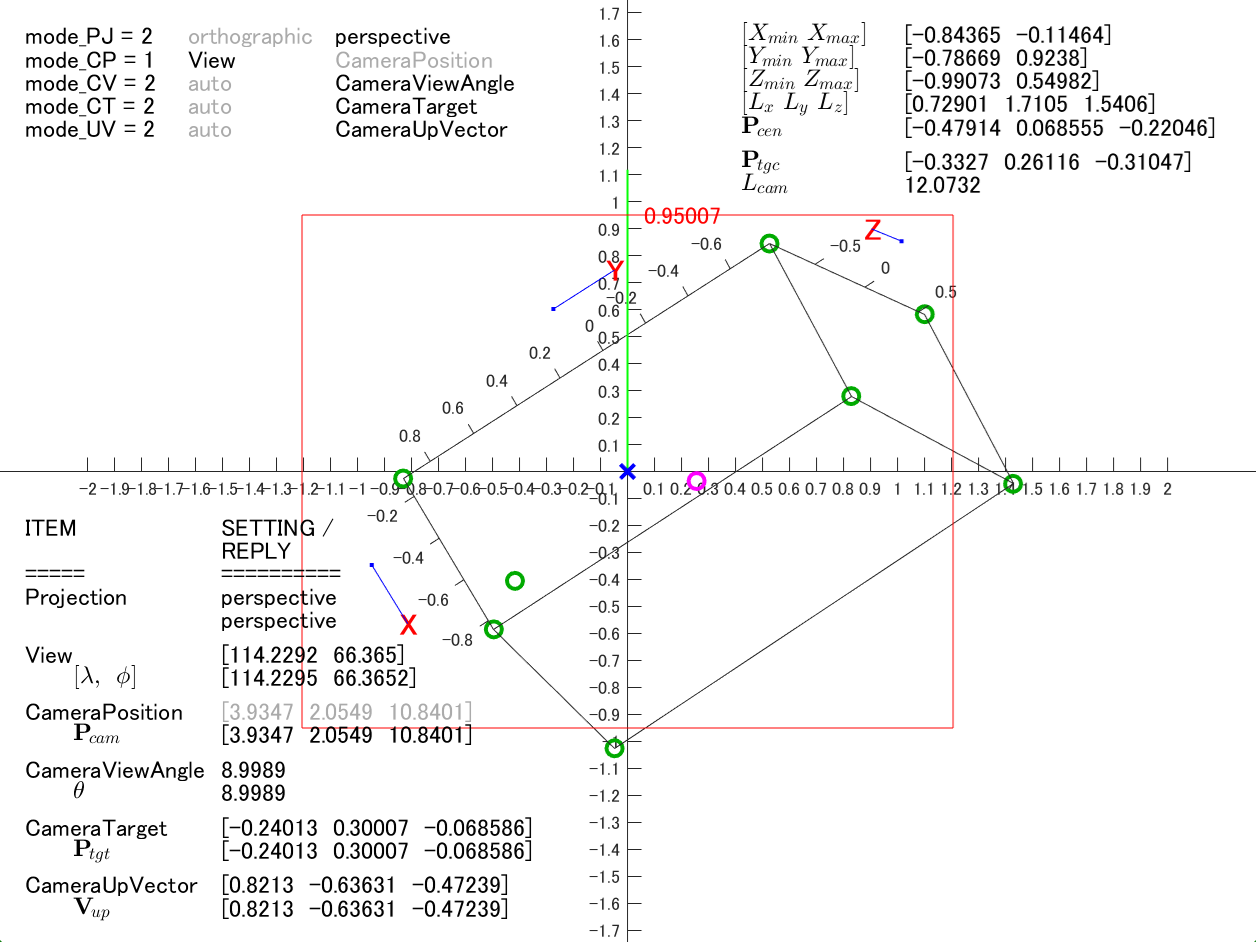
以上の2点をも考慮に入れて MATLAB の三次元プロットのアルゴリズムを推定し、それに沿った検証プログラムを作成しました。その出力結果の一例を図13に示しています。この図は次の三層が重なった構造になっています。
- 第1層は、赤枠を表示する層です。この層には、プロパティの設定値や返り値などの値も表示しています。
- 第2層は、純粋に MATLAB 本来の流儀だけに沿って作図される三次元プロット層です。アルゴリズムの検証だけであれば複雑なプロットまでは必要ないので、描画される観察対象は作図箱だけです。図10に示した作図箱の各パラメータは、実行の都度、乱数で生成されます。また各 ………Mode プロパティの選択に応じて、設定が必要になるプロパティ値も乱数で与えられます。
- 第3層は十文字座標の二次元プロット層です。推定したアルゴリズムに沿って、第2層と同一の乱数を使って作図箱の頂点の位置を計算し、緑色の〇印でマーキングしています。緑色の〇印マーカーが、第2層の作図箱の頂点にピッタリと一致していれば、推定したアルゴリズムが正しいことが確認できます。
ここで、地味ではあっても大切なこととして、第2層の三次元図と第3層の二次元図では、両図のスケールが一致していることが挙げられます。しかし、「正投影法で CameraTarget を指定」の場合だけは、それぞれ個別のスケールとなってしまいます。これは、MATLAB の特殊な投影方法に起因するものですのでお目溢しください。
図13の左上に示しているように、5 種類の動作モードのそれぞれについて 2 つの選択肢があります、したがって、アルゴリズムの確認は $2^5{=}32$ 種類の全ての組み合わせについて行わなければなりません。それにも怯まず、全ての種類について飽きるほどプログラムを実行しました。しかし、最終的に行き着いたプログラムでは、緑〇のマーキング位置がズレたことはありません。推定したアルゴリズムはかなり正しそうです。
プログラム
具体的な推定アルゴリズムは本文中には記載しておりません。下記のプログラムを参照ください。詳細なコメントを付記しているので読みやすいと思います。全体で 650 行程度ありますが、推定アルゴリズムに直接関係するのは 247~376 行あたりです。
ここをクリックしてプログラムを開/閉
% view_point31.m
% 三次元データを二次元図に投影するための推定アルゴリズムの妥当性を確認
% 方法:
% ① 三次元の作図箱を MATLAB 本来の作図方法で描かせる。
% ② 推定したアルゴリズムにより、
% 作図箱の各頂点の本来あるべき位置を計算する。
% ③ 二次元図にその推定位置をマーキングする。
% ④ 三次元図と二次元図を重ねてみて、
% 頂点とマーキングが一致することを確認。
clear
close all
% 投影法の選択
mode_PJ=2; % 1: 正投影法、 2: 透視投影法
% CameraPositionの設定方法を選択
mode_CP=2; % 1: auto(Viewなどで決まる)、 2: 値を指定(manual)
% CameraViewAngle の設定方法を選択
mode_CV=2; % 1: auto、 2: 値を指定(manual)
% CameraTarget の設定方法を選択
mode_CT=1; % 1: auto、 2: 値を指定(manual)
% CameraUpVector の設定方法を選択
mode_UV=1; % 1: auto、 2: 値を指定(manual)
% データの入力方法
method_IN=1; % 1: auto(乱数)、 2: 手入力
% 手入力データ
% ============
% とりあえず設定はしておくが、method_IN==1 の時には、後で乱数データ
% によって上書きされて値が変わる。
% また、「仮値」とは、プロパティの設定モードが auto のときには、
% 設定はしても採用されないことがあることを示している。
% 作図箱のデータ BOX [Xmin Xmax Ymin Ymax Zmin Zmax]
% 方位角、仰角の仮値 azx, elx
% 視点までの距離の仮値 Lcamx
% 画角の仮値 cvax
% CameraTarget の仮値 Ptgx
% CameraUpVector の仮値 cuvx
%{
% すべてが正しい例
% (mode_** の設定は 2,1,2,2,2 とすること)
BOX=[-0.84365 -0.11464 -0.78669 0.9238 -0.99073 0.54982];
azx=114.2292; elx=66.365;
Lcamx=5; % dummy
cvax=8.9989;
Ptgx=[-0.24013 0.30007 -0.068586];
cuvx=[0.8213 -0.63631 -0.47239];
%}
% View と CameraViewAngle の返り値がおかしい例
% (mode_** の設定は 2,2,1,1,1 とすること)
BOX=[-0.78888 0.18766 -0.68956 -0.43454 -0.99868 -0.43281];
azx=18.2919; elx=66.7624;
Lcamx=2.4225;
cvax=10; % dummy
Ptgx=[0 0 0]; % dummy
cuvx=[0 0 1]; % dummy
% ================
% 従属的に決まる値
Xmin=BOX(1);
Xmax=BOX(2);
Ymin=BOX(3);
Ymax=BOX(4);
Zmin=BOX(5);
Zmax=BOX(6);
% ===================
% === 既定 figure ===
% ===================
fg0=figure(1); % 既定の figure を生成
Pf=fg0.Position; % 既定の figure の配置情報を取得
% =================
% === 既定 axes ===
% =================
axes; % 既定の axes を生成
ax0=gca;
Pa=ax0.Position; % 既定の axes の配置情報を取得
Hrp=Pf(4)*Pa(4); % axes の既定の pixel サイズを取得
Wrp=Pf(3)*Pa(3); % Wrp:幅、Hrp:高さ [px]
Kasp=Wrp/Hrp; % axes の既定の アスペクト比を取得
close 1; % 用済みの旧 figure を削除
% =========================
% === サイズ拡張 figure ===
% =========================
% 既定サイズ axes の周辺領域を広げるため、大きな figure を用意する
fg1=figure(1); % 同一図番で figure を再生成
fg1.Color='w'; % 背景は白色
s_size=get(0,'ScreenSize'); % スクリーンサイズを取得 [px]
% [1 1 width height]
Xo=s_size(3)/2; % figure と axes の中心点の座標 [px]
Yo=s_size(4)/2-20;
Ks=1.5; % figure 領域の拡大倍率
fg1.Position=[Xo-Ks*Pf(3)/2 Yo-Ks*Pf(4)/2 Ks*Pf(3) Ks*Pf(4)];
% figure の拡張処理
% ======================
% === 赤枠(第1層) ===
% ======================
% 既定と同一サイズの axes を配置し、外縁に赤枠を描く。
% なお、figure と axes の中心は一致させる。
axes; % 既定の axes を生成
ax1=gca;
ax1.Position=[(1-Pa(3)/Ks)/2 (1-Pa(4)/Ks)/2 Pa(3)/Ks Pa(4)/Ks];
% 既定サイズの axes の配置位置を、
% 新 figure 上の normalized スケ
% ールで指定。
axis([-1 1 -1 1]); % ここでは axis equal にはしない
axt=axis; % axes のフルスケール値を取得
x0=axt(1); x1=axt(2); y0=axt(3); y1=axt(4); % axes 外周を
plot([x0 x1 x1 x0 x0],[y0 y0 y1 y1 y0],'r'); % 赤枠で囲む
axis(axis); % axis の値は4行前に宣言した値をそのまま保持して
% いるのだが、ここで再宣言しておかないと、これ
% 以降で赤枠外に追加 plotしたときに、赤枠の大き
% さが変えられてしまう。
% (text の追加だけなら問題なし)★★★★
hold on
axis off; % 座標軸は削除
Pax=ax1.Position; % 赤枠の位置情報を取得 [normalized]
ax1.Color='none'; % 背景は透明
% ================================
% === 視線関連定数の乱数を設定 ===
% ================================
if method_IN==1 % 乱数設定が指示された場合、
% 手入力済データに乱数を上書き。
% 作図箱の端点の座標を乱数で生成
n=0;
while true
n=n+1;
Pbox=(sort(rand([2 3]))-0.5)*2; % 端点の座標
if min(Pbox(2,:)-Pbox(1,:))/max(Pbox(2,:)-Pbox(1,:))>0.2;
% 細過ぎや薄過ぎの作図箱は不採用
break
end
if n>100
error('適度な形状の作図箱が見つかりません');
end
end
Xmin=Pbox(1,1);
Xmax=Pbox(2,1);
Ymin=Pbox(1,2);
Ymax=Pbox(2,2);
Zmin=Pbox(1,3);
Zmax=Pbox(2,3);
% 以降、「仮値」は、プロパティの設定モードが auto のときには、
% 設定はしても採用されないことがあることを示す。
% 方位角、仰角の仮値を乱数で生成
azx=(rand-0.5)*2*180;
elx=(rand-0.5)*2*90;
% 視点までの距離の仮値を乱数で生成
Lcamx=2+10*rand;
% 画角の仮値を乱数で生成
cvax=7+5*rand;
% CameraTarget の仮値を乱数で生成
Ptgx=(rand([1 3])-0.5)*1;
% CameraUpVector の仮値を乱数で生成
cuvx=(rand([1 3])-0.5)*2;
end
% 従属的に決まる値
Lx=Xmax-Xmin; % 作図箱の各辺の長さ
Ly=Ymax-Ymin;
Lz=Zmax-Zmin;
Pcen=([Xmin Ymin Zmin]+[Xmax Ymax Zmax])/2; % 作図箱の中心座標
% =========================
% === 3D axes(第2層) ===
% =========================
% ===== MATLAB の通常コマンドによる自動描画 =====
ax2=axes('Position',Pax); % 赤枠と同サイズの axes 層を重ねる
hcen=plot3(Pcen(1),Pcen(2),Pcen(3),'om','MarkerSize',8,'LineWidth',2);
% 作図箱の中心にマゼンタ色の〇印
hold on
box on; % 作図箱の各辺を可視化
axis equal;
axis([Xmin Xmax Ymin Ymax Zmin Zmax]); % 作図箱の大きさと位置を指定
ax2.Color='none'; % 第2層の背景は透明
if mode_PJ==2 % 透視投影法の指定があるとき
ax2.Projection='perspective'; % 指定に従う。
end
if mode_CP==1 % 視点 Pcam を View で指定するとき
ax2.View=[azx elx]; % 方位角、仰角の設定
Lcam=5*sqrt(Lx^2+Ly^2+Lz^2); % Pcen から Pcam までの距離
Pcam=Pcen+Lcam*[cosd(elx)*[cosd(azx-90) sind(azx-90)] sind(elx)];
% 視点の座標
% ここでは不使用。後で使う。
elseif mode_CP==2 % 視点 Pcam を CameraPosition で指定
Pcam=Pcen+Lcamx*[cosd(elx)*[cosd(azx-90) sind(azx-90)] sind(elx)];
ax2.CameraPosition=Pcam; % Pcam 座標を設定
Lcam=norm(Pcam-Pcen); % Pcen から Pcam までの距離
% ここでは不使用。後で使う。
end
if mode_CV==2 % CameraViewAngleMode が manual のとき
ax2.CameraViewAngle=cvax;
end
if mode_CT==2 % CameraTargetMode が manual のとき
ax2.CameraTarget=Ptgx;
Ptgt=Ptgx;
elseif mode_CT==1 % CameraTargetMode が auto のとき
Ptgt=Pcen;
end
% Pcam と Ptgt を通る直線上にある、Pcam から距離 Lcam だけ先の点の座標
Ptgc=Pcam+Lcam*(Ptgt-Pcam)/norm(Ptgt-Pcam);
% CameraTarget Ptgt に青×印
htgt=plot3(Ptgt(1),Ptgt(2),Ptgt(3),'xb','MarkerSize',10,'LineWidth',2);
htgt.Clipping='off'; % 青×印が6角形外にあっても表示
uistack(hcen,'top'); % マゼンタ〇印は、青×印よりも上層
if mode_UV==2 % CameraUpVectorMode が manual のとき
ax2.CameraUpVector=cuvx;
Vu=Ptgt+cuvx; % 始点を Ptgt に置いたときの
% CameraUpVector の先端
huv=plot3([Vu(1) Ptgt(1)],[Vu(2) Ptgt(2)],[Vu(3) Ptgt(3)],'g', ...
'LineWidth',1); % CameraUpVector の緑色の線
huv.Clipping='off'; % 緑色の線は6角形外にあっても表示
end
% =========================
% === 2D axes(第3層) ===
% =========================
% 推定した描画アルゴリズムの正否確認ための描画
% 座標の準備
ax3=axes('Position',Pax); % 赤枠と同サイズの axes 層を重ねる
hold on
axis equal;
axis([Kasp*[-1 1] -1 1]*2); % 目盛り値の範囲を決めているだけ。
% あとで、Lcam と CameraViewAngle
% を第2層と同値にしているので、座
% 標のスケールが変わる訳ではない。
ax3.CameraPosition=[0 0 Lcam]; % この約 10 行あとで、Pcam が
% [0 0 Lcam] となるような座標変換を
% 施しているので、それに沿った
% Pcam の再設定である。
ax3.CameraViewAngle=cvax; % 当面、manual の指定値で作図する。
% auto モードのときは、あとで修正。
ax3.Clipping='off';
ax3.Color='none'; % 第3層の背景は透明
ax3.XAxisLocation = 'origin'; % 原点を中心にした
ax3.YAxisLocation = 'origin'; % 十文字座標軸
xticks([-2:0.1:2]);
yticks([-2:0.1:2]);
box off; % axes の外枠は非表示
% ===== 推定アルゴリズムによる投影変換の計算 =====
Nr=(Pcam-Ptgt)/norm(Pcam-Ptgt); % 仮想赤枠面の、視点方向
% の単位法線ベクトル
Nz=[0 0 1]; % z 軸方向の単位ベクトル
Nw=cross(Nz,Nr)/norm(cross(Nz,Nr));
% 視点から見て仮想赤枠面内で
% 右向きの単位ベクトル
Nh=cross(Nr,Nw); % 視点から見て仮想赤枠面内で
% 上向きの単位ベクトル
% 三次元座標上の仮想赤枠の特定点
Pa1=Nh; % 仮想赤枠中心から上へ 1.0 の点
Pa2=Nw; % 仮想赤枠中心から右へ 1.0 の点
Pa3=Lcam*Nr; % 仮想赤枠中心から見た視点
% 仮想赤枠の中心が原点 [0 0 0] と一致するように平行移動し、
% さらに、仮想赤枠を x,y 面内に埋め込み、
% 上辺・下辺が x 軸に、左辺・右辺が y 軸に平行になるように
% 三次元回転したとき、上記各点 Pa1,Pa2,Pa3 の座標は下記となるべき。
Pb1=[0 1 0];
Pb2=[1 0 0];
Pb3=[0 0 Lcam];
% 上記の座標変換のために、原点を中心とした三次元回転行列を求める
MPa=[Pa1' Pa2' Pa3']; % 変換前の点群の座標を示す行列
MPb=[Pb1' Pb2' Pb3']; % 変換後 〃
Mconv=MPb*inv(MPa); % 原点を中心にした三次元回転行列
% 【平行移動 & 三次元回転】前の作図箱の各頂点の座標
Va=[[Xmin Ymin Zmin]' [Xmax Ymin Zmin]' ...
[Xmax Ymax Zmin]' [Xmin Ymax Zmin]' ...
[Xmin Ymin Zmax]' [Xmax Ymin Zmax]' ...
[Xmax Ymax Zmax]' [Xmin Ymax Zmax]'];
% 【平行移動 & 三次元回転】後の作図箱の各頂点の座標
Vb=Mconv*(Va-Ptgc'*(ones(1,size(Va,2))));
% Projection の種類により、二次元へのデータ化の方法は異なる。
if mode_PJ==1 % === 正投影のとき ===
Vb(3,:)=[]; % z 軸データのみ削除して二次元化。
if mode_CT==1 % CameraTargetMode が auto のとき
Vc=Vb; % そのまま、最終データ。
elseif mode_CT==2 % CameraTargetMode が manual のとき
Vc=Vb*Lcam/norm(Pcam-Ptgt); % サイズを補正して最終データ。等価
% 的に、Ptgt 面に正投影された像を、
% Ptgc 面に透視投影したことになる。
end
elseif mode_PJ==2 % === 透視投影のとき ===
Kps=Lcam./(Lcam-Vb(3,:)); % z 成分による
% 各点の x,y 成分の補正倍率
Vc(1,:)=Vb(1,:).*Kps; % x 成分の補正
Vc(2,:)=Vb(2,:).*Kps; % y 成分の補正
end
% CameraUpVectorMode が manual のとき、CameraUpVector が二次元座標上で
% 真上を向くように、点群全体をまとめて回転。
if mode_UV==2
cuv2=Mconv*cuvx'; % 三次元の Up ベクトルを回転して、
cuv2(3)=[]; % x,y 面上に投影し、二次元ベクトル化
varphi=90-atan2d(cuv2(2),cuv2(1));
% そのベクトルを真上に向けるための回転角
Mrot=[cosd(varphi) -sind(varphi) ; sind(varphi) cosd(varphi)];
% 原点を中心にした二次元回転行列
Vc=Mrot*Vc; % 二次元化された画像全体を回転
end
% CameraViewAngleMode が auto のときの縦画角の計算
% 大きさの制限を赤枠の上下で受けるか、左右で受けるかにより別処理。
MaxH=max(abs(Vc(2,:)));
MaxW=max(abs(Vc(1,:)));
if MaxW/MaxH>Kasp % 赤枠の左右で CameraViewAngle が決まるとき
varK=MaxW/Kasp; % 赤枠に収めるのに必要な画像倍率はこれ。
else % 赤枠の上下で CameraViewAngle が決まるとき
varK=MaxH; % 赤枠に収めるのに必要な画像倍率はこれ。
end
% CameraViewAngleMode が auto のときに必要となる最終的な縦画角の値
cva_auto=2*atand(varK/Lcam);
if mode_CV==1 % CameraViewAngleMode が auto のとき
ax3.CameraViewAngle=cva_auto;
% 新しい CameraViewAngle を設定
cva_final=cva_auto;
elseif mode_CV==2 % CameraViewAngleMode が manual のとき
cva_final=cvax; % 最初の指定値がそのまま最終値となる。
end
% 作図箱の8個の頂点の予想位置を緑色の〇印でマーキング。
% この緑〇印と三次元プロットの頂点の位置が完全に重なれば、
% 推定した描画アルゴリズムが正しいことが証明されたことになる。
plot(Vc(1,:),Vc(2,:), ...
'o','LineWidth',2,'Color','#0a0','MarkerSize',8);
% ====================================================
% === 確認のため、赤枠座標上にモード設定内容を表示 ===
% ====================================================
axes(ax1); % 赤枠座標の呼び出し
% 文字書き込み位置の準備
% 赤枠の axis を [-1 1 -1 1] としたスケールにて
xt0=-1.85; % 文字群の左端
yt0=1.25; % 文字群の下端
ytp=0.09; % 文字の行間の基本ピッチ
xp1=0.5; % 左端からのインデント
xp2=0.95; % 〃
yt=[1:5]; % 各行の下端からの位置
yt=yt*ytp+yt0;
text(xt0,yt(5),['mode\_PJ' ' = ' num2str(mode_PJ)],'FontSize',12);
% Projection の種類
text(xt0,yt(4),['mode\_CP' ' = ' num2str(mode_CP)],'FontSize',12);
% CameraPosition の設定方法
text(xt0,yt(3),['mode\_CV' ' = ' num2str(mode_CV)],'FontSize',12);
% CameraViewAngle の設定方法
text(xt0,yt(2),['mode\_CT' ' = ' num2str(mode_CT)],'FontSize',12);
% CameraTarget の設定方法
text(xt0,yt(1),['mode\_UV' ' = ' num2str(mode_UV)],'FontSize',12);
% CameraUpVector の設定方法
htx(5,1)=text(xt0+xp1,yt(5),'orthographic','FontSize',12);
htx(4,1)=text(xt0+xp1,yt(4),'View','FontSize',12);
htx(3,1)=text(xt0+xp1,yt(3),'auto','FontSize',12);
htx(2,1)=text(xt0+xp1,yt(2),'auto','FontSize',12);
htx(1,1)=text(xt0+xp1,yt(1),'auto','FontSize',12);
htx(5,2)=text(xt0+xp2,yt(5),'perspective','FontSize',12);
htx(4,2)=text(xt0+xp2,yt(4),'CameraPosition','FontSize',12);
htx(3,2)=text(xt0+xp2,yt(3),'CameraViewAngle','FontSize',12);
htx(2,2)=text(xt0+xp2,yt(2),'CameraTarget','FontSize',12);
htx(1,2)=text(xt0+xp2,yt(1),'CameraUpVector','FontSize',12);
if mode_PJ==1
htx(5,2).Color='#aaa';
else
htx(5,1).Color='#aaa';
end
if mode_CP==1
htx(4,2).Color='#aaa';
else
htx(4,1).Color='#aaa';
end
if mode_CV==1
htx(3,2).Color='#aaa';
else
htx(3,1).Color='#aaa';
end
if mode_CT==1
htx(2,2).Color='#aaa';
else
htx(2,1).Color='#aaa';
end
if mode_UV==1
htx(1,2).Color='#aaa';
else
htx(1,1).Color='#aaa';
end
% ========================================
% === 赤枠座標上に各プロパティ値を表示 ===
% ========================================
% 文字書き込み位置の準備
% 赤枠の axis を [-1 1 -1 1] としたスケールにて
xt0=-1.85; % 文字群の左端
yt0=-1.70; % 文字群の下端
ytp=0.09; % 文字の行間の基本ピッチ
xp1=0.6; % 左端からのインデント
yt=[]; % 各行の下端からの位置
for n=1:6
yt=[yt (n-1)*2.5+[0 1]];
end
yt=[yt max(yt)+[1 2 3]]*ytp+yt0;
% タイトル行の位置も追加
% ==================
% プロパティ名を表示
text(xt0,yt(15),'ITEM','FontSize',12);
text(xt0,yt(13),'=====','FontSize',12);
text(xt0,yt(12),'Projection','FontSize',12);
text(xt0,yt(10),'View','FontSize',12);
text(xt0,yt(9), '$$\hspace{2em}[\lambda,\hspace{0.5em}\phi]$$', ...
'FontSize',12,'Interpreter','latex');
text(xt0,yt(8), 'CameraPosition','FontSize',12);
text(xt0,yt(7), '$$\hspace{2em}{\mathbf{P}}_{\!cam}$$', ...
'FontSize',12,'Interpreter','latex');
text(xt0,yt(6), 'CameraViewAngle','FontSize',12);
text(xt0,yt(5), '$$\hspace{2em}\theta$$','FontSize',12, ...
'Interpreter','latex');
text(xt0,yt(4), 'CameraTarget','FontSize',12);
text(xt0,yt(3), '$$\hspace{2em}{\mathbf{P}}_{\!tgt}$$', ...
'FontSize',12,'Interpreter','latex');
text(xt0,yt(2), 'CameraUpVector','FontSize',12);
text(xt0,yt(1), '$$\hspace{2em}{\mathbf{V}}_{\!up}$$', ...
'FontSize',12,'Interpreter','latex');
% ========================
% プロパティの設定値を表示
% 黒色文字は直接的な設定値。灰色文字は間接的に決まる値。
text(xt0+xp1,yt(15),'SETTING /','FontSize',12);
if mode_PJ==1
text(xt0+xp1,yt(12),'orthographic','FontSize',12);
elseif mode_PJ==2
text(xt0+xp1,yt(12),'perspective','FontSize',12);
end
if mode_CP==1
text(xt0+xp1,yt(10),['[' num2str(azx) ' ' num2str(elx) ']'], ...
'FontSize',12);
text(xt0+xp1,yt(8),['[' num2str(Pcam(1)) ...
' ' num2str(Pcam(2)) ' ' num2str(Pcam(3)) ']'], ...
'Color','#aaa','FontSize',12);
elseif mode_CP==2
text(xt0+xp1,yt(10),['[' num2str(azx) ' ' num2str(elx) ']'], ...
'Color','#aaa','FontSize',12);
text(xt0+xp1,yt(8),['[' num2str(Pcam(1)) ' ' num2str(Pcam(2)) ...
' ' num2str(Pcam(3)) ']'],'FontSize',12);
end
if mode_CV==2
text(xt0+xp1,yt(6),num2str(cvax),'FontSize',12);
elseif mode_CV==1
text(xt0+xp1,yt(6),num2str(cva_auto),'Color','#aaa','FontSize',12);
end
if mode_CT==2
text(xt0+xp1,yt(4),['[' num2str(Ptgt(1)) ...
' ' num2str(Ptgt(2)) ' ' num2str(Ptgt(3)) ']'],'FontSize',12);
elseif mode_CT==1
text(xt0+xp1,yt(4),['[' num2str(Ptgt(1)) ...
' ' num2str(Ptgt(2)) ' ' num2str(Ptgt(3)) ']'], ...
'Color','#aaa','FontSize',12);
end
if mode_UV==2
text(xt0+xp1,yt(2),['[' num2str(cuvx(1)) ...
' ' num2str(cuvx(2)) ' ' num2str(cuvx(3)) ']'],'FontSize',12);
elseif mode_UV==1
text(xt0+xp1,yt(2),'[0 0 1]','Color','#aaa','FontSize',12);
end
% ====================================
% Query によるプロパティの返り値を表示
text(xt0+xp1,yt(14),'REPLY','FontSize',12);
text(xt0+xp1,yt(13),'==========','FontSize',12);
text(xt0+xp1,yt(11),ax2.Projection,'FontSize',12);
aa=ax2.View;
text(xt0+xp1,yt(9),['[' num2str(aa(1)) ' ' num2str(aa(2)) ']'], ...
'FontSize',12);
aa=ax2.CameraPosition;
text(xt0+xp1,yt(7),['[' num2str(aa(1)) ...
' ' num2str(aa(2)) ' ' num2str(aa(3)) ']'],'FontSize',12);
text(xt0+xp1,yt(5),num2str(ax2.CameraViewAngle),'FontSize',12);
aa=ax2.CameraTarget;
text(xt0+xp1,yt(3),['[' num2str(aa(1)) ...
' ' num2str(aa(2)) ' ' num2str(aa(3)) ']'],'FontSize',12);
aa=ax2.CameraUpVector;
text(xt0+xp1,yt(1),['[' num2str(aa(1)) ...
' ' num2str(aa(2)) ' ' num2str(aa(3)) ']'],'FontSize',12);
% ================================================
% === 赤枠座標上に作図箱の位置データなどを表示 ===
% ================================================
% 文字書き込み位置の準備
% 赤枠の axis を [-1 1 -1 1] としたスケールにて
xt0=0.35; % 文字群の左端
yt0=1.03; % 文字群の下端
ytp=0.09; % 文字の行間の基本ピッチ
xp1=0.5; % 左端からのインデント
yt=[1:7]; % 各行の下端からの位置
yt(3:7)=yt(3:7)+0.5;
yt=yt*ytp+yt0;
text(xt0,yt(7),'$$[X_{min}\hspace{0.3em}X_{max}]$$','FontSize',12, ...
'Interpreter','latex');
text(xt0,yt(6),'$$[Y_{min}\hspace{0.3em}Y_{max}]$$','FontSize',12, ...
'Interpreter','latex');
text(xt0,yt(5),'$$[Z_{min}\hspace{0.3em}Z_{max}]$$','FontSize',12, ...
'Interpreter','latex');
text(xt0,yt(4),'$$[L_x\ L_y\ L_z]$$','FontSize',12, ...
'Interpreter','latex');
text(xt0,yt(3),'$${\mathbf{P}}_{\!cen}$$','FontSize',12, ...
'Interpreter','latex');
text(xt0,yt(2),'$${\mathbf{P}}_{\!tgc}$$','FontSize',12, ...
'Interpreter','latex');
text(xt0,yt(1),'$$L_{cam}$$','FontSize',12,'Interpreter','latex');
text(xt0+xp1,yt(7),['[' num2str(Xmin) ' ' num2str(Xmax) ']'], ...
'FontSize',12)
text(xt0+xp1,yt(6),['[' num2str(Ymin) ' ' num2str(Ymax) ']'], ...
'FontSize',12)
text(xt0+xp1,yt(5),['[' num2str(Zmin) ' ' num2str(Zmax) ']'], ...
'FontSize',12)
text(xt0+xp1,yt(4),['[' num2str(Lx) ' ' num2str(Ly) ' ' ...
num2str(Lz) ']'],'FontSize',12)
text(xt0+xp1,yt(3),['[' num2str(Pcen(1)) ' ' num2str(Pcen(2)) ...
' ' num2str(Pcen(3)) ']'],'FontSize',12)
text(xt0+xp1,yt(2),['[' num2str(Ptgc(1)) ' ' num2str(Ptgc(2)) ...
' ' num2str(Ptgc(3)) ']'],'FontSize',12)
text(xt0+xp1,yt(1),num2str(Lcam),'FontSize',12)
% 赤枠の上端位置の二次元、三次元座標スケールによる値を表示
Hr_final=Lcam*tand(cva_final/2); % 赤枠の最終高さの半分
text(0.05,1,num2str(Hr_final),'Color','r','FontSize',12);
% ==========================================================
% === 第2層の三次元図に、軸ラベル と 正方向の矢印を追記 ===
% ==========================================================
% Hr_final の値が決まるまでは、矢印の長さの適値が定まらないため、
% ここにきて、やっと記述できるようになった。
axes(ax2);
ax2.Clipping='off'; % これが無いと矢印が表示されない
% 軸ラベル
hhx=xlabel('X','Color','r','FontSize',15,'FontWeight','bold');
hhy=ylabel('Y','Color','r','FontSize',15,'FontWeight','bold');
hhz=zlabel('Z','Color','r','FontSize',15,'FontWeight','bold');
% 正方向の矢印(のようなもの)
hhx.VerticalAlignment='middle';
hhy.VerticalAlignment='middle';
hhz.VerticalAlignment='middle';
hhx.HorizontalAlignment='center';
hhy.HorizontalAlignment='center';
hhz.HorizontalAlignment='center';
Px1=hhx.Position;
Py1=hhy.Position;
Pz1=hhz.Position;
Px2=Px1+[1 0 0]*0.3*Hr_final;
Py2=Py1+[0 1 0]*0.3*Hr_final;
Pz2=Pz1+[0 0 1]*0.3*Hr_final;
plot3([Px1(1) Px2(1)],[Px1(2) Px2(2)],[Px1(3) Px2(3)],'b' );
plot3(Px2(1),Px2(2),Px2(3),'.b');
plot3([Py1(1) Py2(1)],[Py1(2) Py2(2)],[Py1(3) Py2(3)],'b' );
plot3(Py2(1),Py2(2),Py2(3),'.b');
plot3([Pz1(1) Pz2(1)],[Pz1(2) Pz2(2)],[Pz1(3) Pz2(3)],'b' );
plot3(Pz2(1),Pz2(2),Pz2(3),'.b');
axes(ax1); % 赤枠 axes を最上レイヤーに。
% (プロパティ情報が覆い隠されないように)
%{
% おかしな値に赤矢印をつける(通常はコメント化)
[xan1,yan1]=axe2fig(gca,[-0.38 -0.68],[-0.76 -0.76]);
annotation('arrow',xan1,yan1,'LineWidth',2,'Color','r');
[xan2,yan2]=axe2fig(gca,[-0.7 -1.0],[-1.2 -1.2]);
annotation('arrow',xan2,yan2,'LineWidth',2,'Color','r');
% ==================================================================
% axes の座標値を figure の normalized 単位に変換するローカル関数
function [x1_2,y1_2]=axe2fig(haxe,x1x2,y1y2)
% 【入力】
% haxe: 現在アクティブになっている axes のハンドル。
% 呼び出し側での引数は「gca」とすること。
% x1x2: axes 上の点の x座標群(点の数に相当する要素数の行ベクトル)
% y1y2: 〃 y 〃
% 【出力】
% x1_2: x1x2 を normalized 単位に変換後の行ベクトル
% y1_2: y1y2 〃
ap=haxe.Position;
al=ap(1); ab=ap(2); aw=ap(3); ah=ap(4);
area=axis(haxe);
xmin=area(1); xmax=area(2); ymin=area(3); ymax=area(4);
x1_2=aw*(x1x2-xmin)/(xmax-xmin)+al;
y1_2=ah*(y1y2-ymin)/(ymax-ymin)+ab;
end
%}
ただし、観察対象や仮想赤枠に対しては、あらかじめ平行移動と回転の操作を施し、図9が図14の状態になるように変換して計算を楽にしています。仮想赤枠の中心を原点とし、右方向を $x$ 軸、上方向を $y$ 軸と一致させています。この結果、$\mathbf{P}_{\!cam}$ は $z$ 軸上に乗ることになります。
また、Projection の種類による投影像の差異を説明するために、図15には正投影法、図16には透視投影法の原理を示しています。なお、投影法の特徴を分かり易く伝えるため、これらの図だけは他の図とは表現方法を変え、$L_{cam}$ を短かめにし、第4象限上方から観察するようにしています。
4.2.3 三次元と二次元の関連性
三次元プロットと二次元プロットでは、コマンドも plot3 と plot のように異なっているし、全く別の動作モードのように見えますが、ある程度の連続性はあります。これを心得ておくと、一部の疑問点の解消に役立つこともあります。
-
本来、平面的で単純な二次元プロットにおいては、CameraViewAngle $\theta$ や視点距離 $L_{cam}$ などという高位の概念は不要のように思われます。しかし、二次元座標でも、CameraPosition プロパティを読み取れば、返り値は [$x_c$ $y_c$ $L_{cam}$] のように三次元形式で返されます( [$x_c$, $y_c$ は赤枠の中心座標、$L_{cam}$ はスクリーン面から仮想視点までの距離] )。また、CameraViewAngle の返り値 $\theta$ も当たり前のように読み取れます。この場合も、(1), (2)式はそのまま成立し、赤枠の大きさと CameraViewAngle $\theta$ や $L_{cam}$ との間の整合性は三次元のときと同様に保たれます。これにより、図13のように二次元図と三次元図を重ねた場合、両図に、同一の CameraViewAngle と、$L_{cam}$ が同一となるような CameraPosition を設定しておけば、両図のスケールを同一にすることができます。
-
普通、二次元プロットでは、わざわざ CameraPosition を設定するようなことはありません。この場合、CameraPosition プロパティの返り値に含まれる $L_{cam}$ の値は次のような値になっています。
$$
L_{cam}=5\sqrt{{L_x}^2+{L_y}^2+4}\tag{4}
$$
二次元とはいいながら、(3)式で $L_z{=}0$ と置くのではなく、スクリーン面を挟んで、手前と背後に厚さ 1.0 の仮想 $z$ 層を持つ作図箱が存在しているイメージです。
5.利用上の注意点
5.1 一部の返り値がおかしい
図17には、別の条件で実行した検証結果を示しています。緑〇印の位置については問題ありませんが、左下に表示されている View と CameraViewAngle の値(赤矢印)が問題です。それぞれのプロパティ値は上下 2 段に示されていますが、上段が本来とるべき値、下段がクエリに対する返り値です。これらの値は一致しているべきなのですが、ここでは異なった値を示しています。
図17 推定描画アルゴリズムの検証画面(返り値がおかしい例)
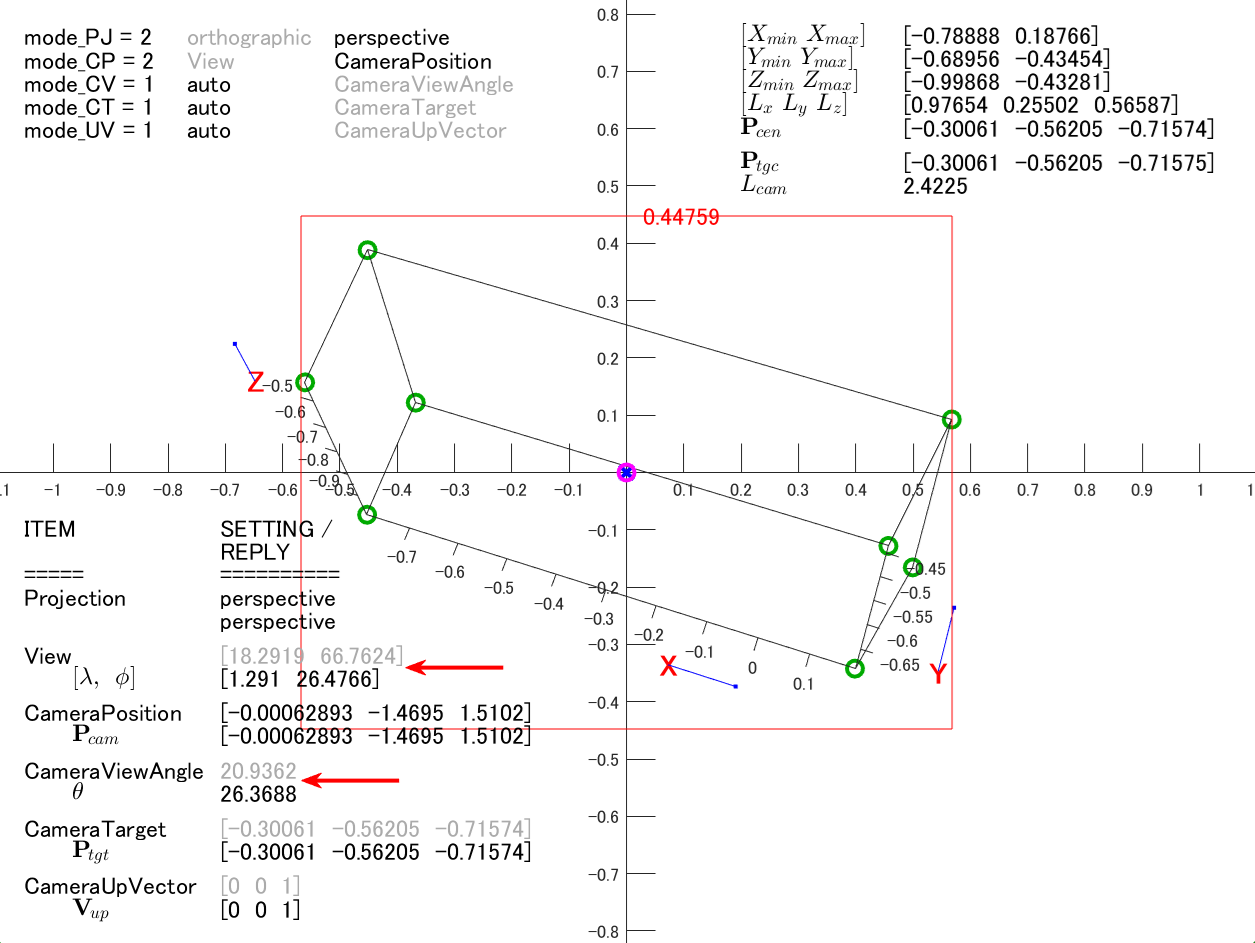
この検証では、視点を View ではなく CameraPosition $\mathbf{P}_{\!cam}$ で指定しているので、上段に示している View は直接の設定値ではありません。$\mathbf{P}_{\!cam}$ と $\mathbf{P}_{\!cen}$ の値から容易に逆算できる本来あるべき View の値です。間接的に導いた値であることを示すために淡色の文字で表記しています。
また、ここでは、CameraViewAngleMode は auto の状態なので、CameraViewAngle $\theta$ も直接には設定していません。したがって、この上段の値も、緑〇印の位置を求める過程で間接的に導出された CameraViewAngle の値を示しています。この計算はやや複雑なので、むしろ、上段の値の方の信憑性を疑われかねませんが、それは杞憂です。MATLAB の返り値をそのまま使って緑〇印の位置を計算すると、全く異なった位置にズレてしまいます。しかし、上段の値を使用すれば正しい図が描かれます。
これら二つのプロパティの返り値の性質について調べたところ、次のようなことが分かりました。
CameraViewAngle
auto モード中なので、投影画像は赤枠内に押し込められます。その画像の大きさが赤枠の上下で制限されているときだけは正しい値を返します。しかし、赤枠の左右で制限されるときには値がおかしくなります。普通の赤枠では横幅の方が大きいため、おかしな値になる頻度は下がりますが、続けて実行していればいつかは必ず発生します。どうも、赤枠のアスペクト比が恒常的に 1.0 であるかのように錯覚して返り値を計算しているように見えます。おかしな返り値をそのまま使って作図すると、本来よりも小さい画像になってしまいます。
View
作図箱が正六面体(立方体)で CameraTargetMode が auto のときだけは正しい値を返します。それ以外では奇妙で複雑な値を返してきます。一例を示せば図18のようになります。何か有益な意味を持った値のような気もしますが、残念ながら、この図からは何も思いつきません。
図18 CameraPosition を指定したときの View による返り値
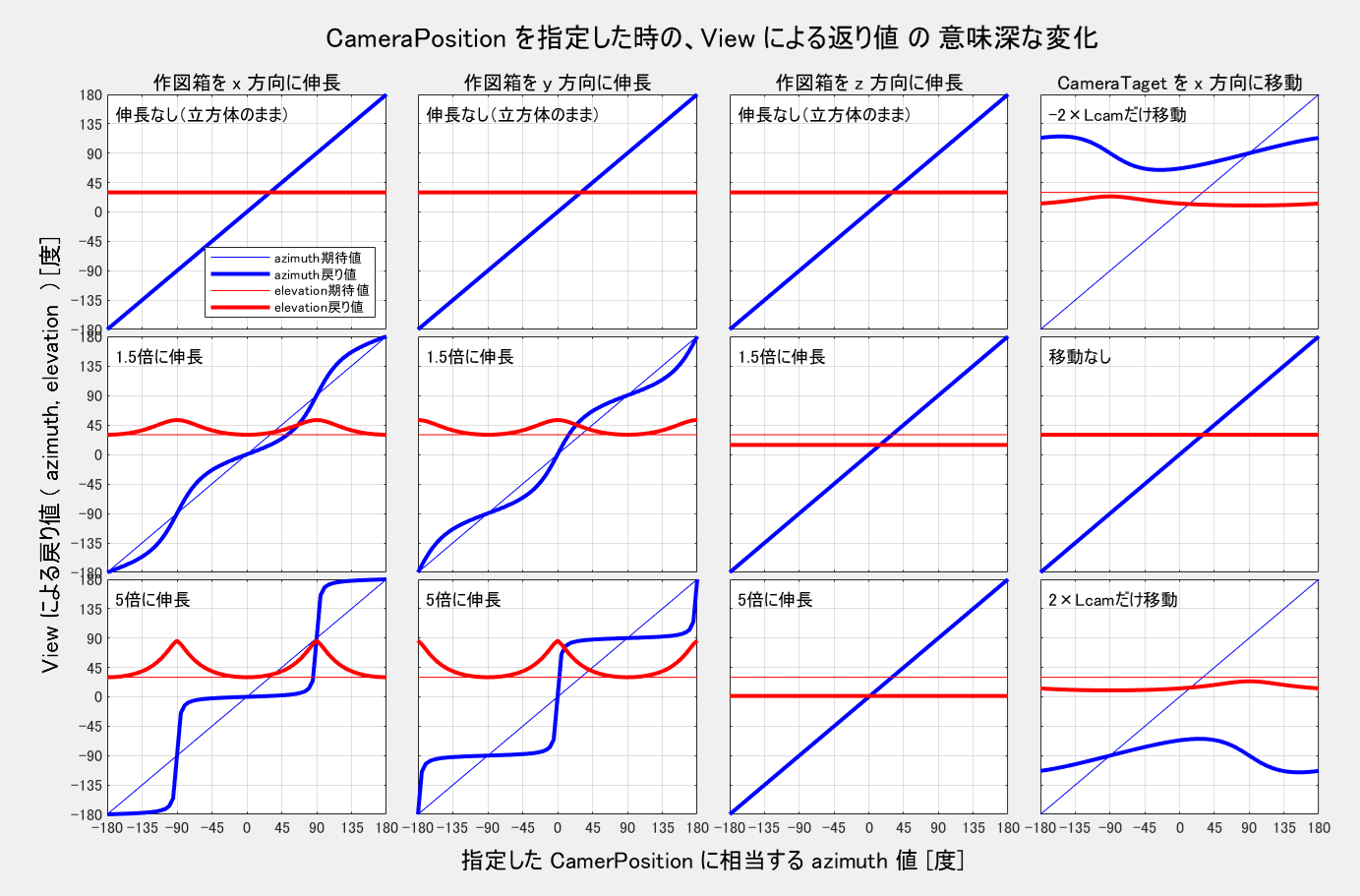
5.2 その他
それほど大きな問題ではありませんが、その他の細かい注意点を挙げておきます。
- 今までの説明からも明らかですが、View と CameraPosition の動作はお互いに競合しています。その点を十分に認識して使用する必要があります。MATLAB のドキュメンテーションには次のような記述がありますが、このことを言っているのかどうか良くは分かりません。別件であるならば、これも注意点の一つになります。
方位角と仰角を設定すると、カメラ関連の他のプロパティがリセットされることがあります。最適な結果を得るには、カメラ関連の他のプロパティを設定する前に、方位角と仰角を設定してください。
- CameraTarget や CameraUpVector を指定したり、CameraViewAngle と CameraPosition を同時指定したりすると、マウスを使った figure の「三次元回転」操作が不便になります。これらの図を回転操作しようとすると、強制的に auto モードに切り替り、画像が一瞬にして想定外の形式に変わります。こうなると、思考が中断されて士気が低下してしまいます(「表示の復元」マークをクリックすれば元には戻せます)。
- ドキュメンテーションには、CameraViewAngle の既定値が 6.6086 度とあります。しかし、この意味を十分には掴みきれていません。既定値の定義を「具体値を指定しないときに自動的に設定される値」と解釈すると、【 View ≡ [-37.5 30]、CameraPosition ≡ 「View と $L_{cam}$ に依存」、Projection ≡ orthographic、CameraTarget ≡ $\mathbf{P}_{\!cen}$、CameraUpVector ≡ [0 0 1] 】については納得できます。しかし、値は未設定のまま CameraViewAngleMode を manual にして三次元図を描かせても、CameraViewAngle の返り値は 6.6086 にはなりません。作図箱のパラメータなどによっても変わりますが別の値になります。確かに、二次元図で axis normal の場合には、多くのケースで 6.6086 が返りますが、この値でなければならない必然性が分かりません。強いて、三次元図において 6.6086 が返る条件を探してみると、CameraViewAngleMode が auto、Projection が orthographic の状態で、$L_x{=}L_y{=}L_z$ かつ View が [0 90] の場合です。
6.おわりに
モヤモヤしていた点が当初よりは解消されました。しかし、まだ、不可解な返り値など、考えが及ばない問題が残っています。何かお気づきの点があれば、コメントいただければ幸いです。