はじめに
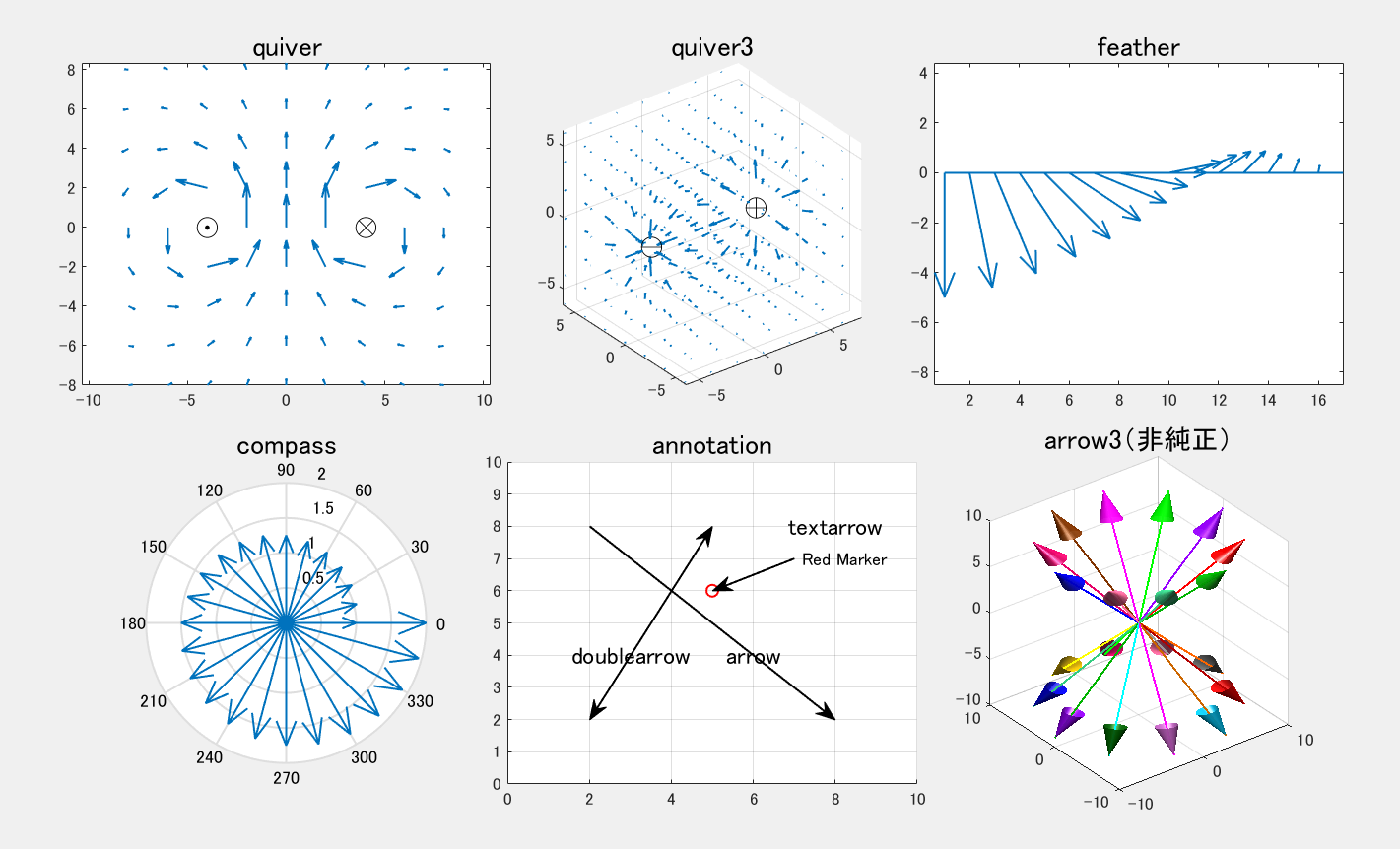
MATLAB のグラフを描いていると、線の先端を矢印にしたくなることが良くあります。この希望を叶えるために色々と調べてみると、MATLAB には既に矢印を表示するコマンドが沢山あることが分かります(その一部を図1に示しています)。
しかし、quiver, quiver3, feather, compass は、それぞれの目的に合わせて機能が特化されており、汎用的な矢印としての自由な流用は難しそうです。また、annotation 用の矢印は、座標の単位系が一般の plot 用とは異なるため、利用するには一手間かかって面倒です。さらに、MATLAB の File Exchange には arrow3 という矢印ツールもあります。しかし、純正品ではないため標準では組み込まれていません。機能的には高級ですが、やや凝りすぎの感もあって地味な用途には馴染みません。
このように、どの矢印も「帯に短し、襷に長し」で、目的に合ったコマンドはなかなか見当たりません。線を矢印に変えるにはたった2本の短い線を追加すれば済むことですが、これが意外と厄介です。水平線や垂直線の先端に追加するのであればまだ何とかなりますが、曲線や傾いた直線になると、もう面倒になってヤル気が失せてしまいます。
そこで、矢印をもっと自由に気軽に扱えるように、比較的軽い装備のローカル関数を作ってみました。なお、この関数は axis equal(全軸等スケール)の環境を前提としています。これ以外の環境では矢印の形が歪むという難点があります。しかし、これは多くの既存のコマンドでも見られる現象なので我慢することにします。
図1 MATLABに既存の矢印関連コマンド
動作確認バージョン: MATLAB R2019a
二次元の矢印を描く関数(plot_arrow2d())
これは 矢印(主軸部+先端部)の一部である先端部のV字だけを描く関数です。関数の引数は、【矢印化したい主軸上の任意の1点】と【矢印の先端の点】の座標 および V字部分の【長さ】と【開き角度】です。戻り値はV字図形のハンドルだけです。描かれるV字は、線幅が 0.5 で黒一色だけですが、ハンドルのプロパティを書き換えれば任意の太さや色に変更できます。具体的なスクリプトについては、後続の関数も含めて、記事の最後にある「図2の描画用プログラム」の項を参照ください。
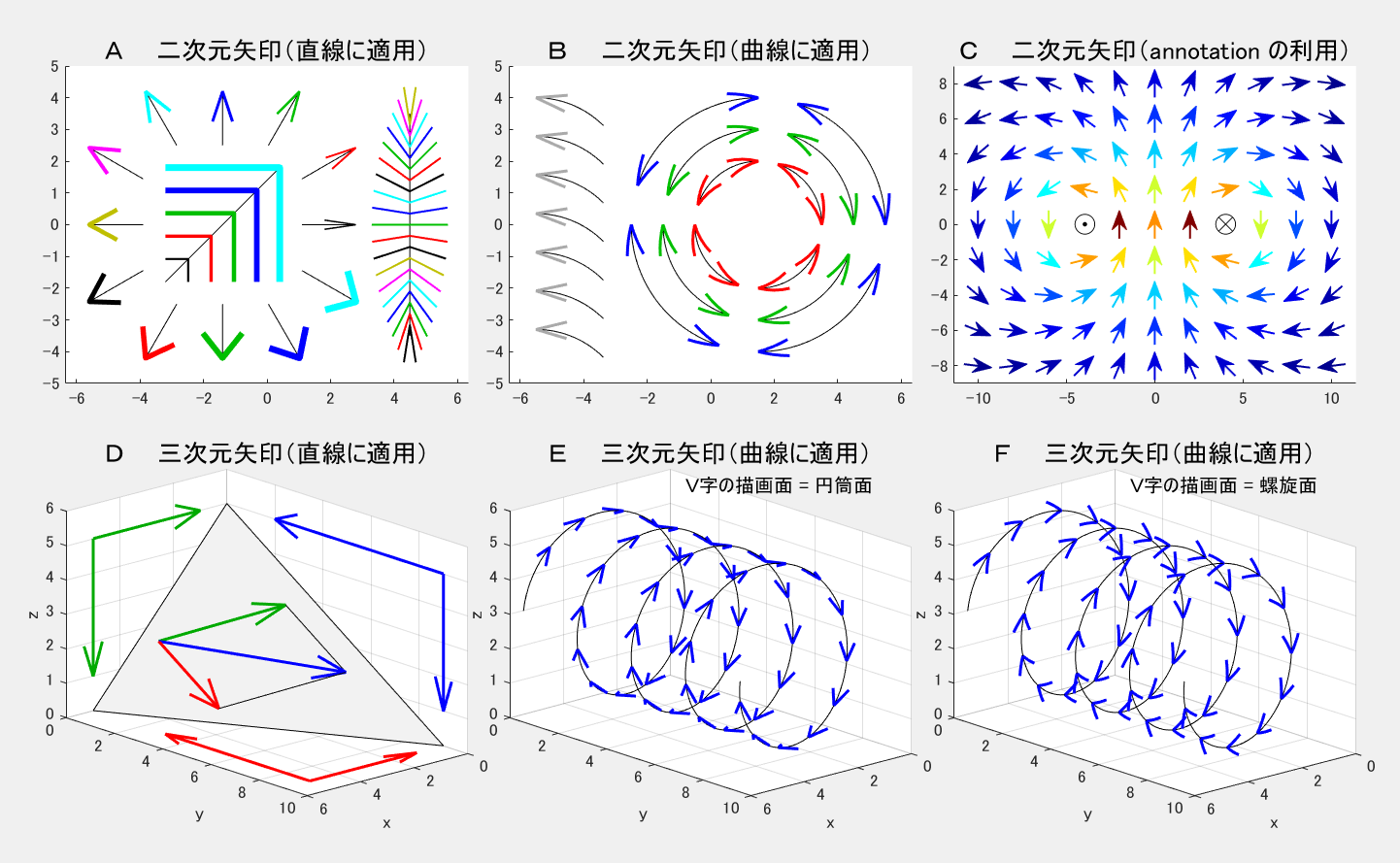
簡素で単純な矢印ですが、お好み次第で図2Aのような色々な使い方が可能です。なお、主軸が直線の場合には問題ありませんが、曲線の場合、その先端にV字を付けたとき、角度的な整合性が悪く不自然さを感じることがあります。その場合でも、入力引数の【矢印化したい主軸上の任意の1点】を、先端に至近の折点ではなく、適度に離れた折点に選び直せば、そこそこ我慢できる程度には修正することができます(図2B左。最下段は無修正、最上段は過修正)。しかし、この少々姑息な手段が受け入れられない場合には、曲率半径を追加指定してV字を湾曲させれば、もっと自然な形に馴染ませることができます(図2B右)。これでもまだ違和感があるときには、オプションの引数でV字の傾き角度を指定すれば、その分だけ遠心力方向に変位するので、ほぼ完璧に修正することができます。
三次元の矢印を描く関数(plot_arrow3d())
二次元の矢印と似たようなものですが、三次元の場合には【どの平面上にV字を描くのか】の指定も必要になります。この描画平面はその法線の向きで指定します。なお、このローカル関数からは、さらに別物の 点群回転(rot_points_3d()) や、平面と垂線の交点の計算(intsec_Plane_and_PerpLine())用のローカル関数も呼び出して利用しています。使用の際には、こちらも忘れずに仲間に入れておいてください。
ところで、描画平面に中途半端な傾きがある場合には、法線のベクトルを求めるのも大変な作業です。これを簡単にできるように、3点の座標から それらを含む平面の法線を求めるローカル関数(find_plane_const()) も添付しておきました。必要に応じてご利用ください。
なお、三次元の矢印では、曲率半径の指定は、主軸の曲線とV字が同一平面内にある場合に限って有益です。それ以外でもエラーにはなりませんが、期待しない結果しか得られません。
これらを利用すると、図2D~Fのような応用が可能です。
アノテーション用矢印の補助ツール(axe2fig())
上で紹介したローカル関数だけでは、矢印の形があまりにも簡素すぎて物足りなさを感じることもあります。そのような場合に備えて、annotation 用の芸術的な矢印も気軽に使えるようにしておきたいものです。この矢印は形が美しいだけでなく、全軸等スケールでなくても歪みは生じない という長所も持っています。
そのために、【axes の座標系で指定された位置情報】を【figure 上の normalized 座標】に変換するローカル関数を作りました(ただし、二次元専用です)。関数の引数は【現在の axes のハンドル(gca)】と【その axes スケールで指定された点群の x,y 座標値】だけです。図1の annotation 用矢印の例や、図2Cもこれを利用して描いています。そのため、異なる座標系のオブジェクトを誤差なくピッタリと重ね合わせることができています。しかし、図2の多くの図では瞬時に作図が終わるのに対し、Cの図だけはかなりの時間がかかるという欠点があります(CORE-i7 で約 0.85 秒。なぜか、ヘルプのドキュメンテーションを開いている場合にはさらに長く 2 秒近くもかかります)。どうも、MATLAB からはあまり歓迎されない利用法のようです。
おわりに
凝った矢印は描けませんが手軽に使えて便利です。お役に立てれば幸いです。
二次元の矢印用関数は、複数のV字を1コマンドで同時処理できるように高機能を追求しました。しかし、三次元用ではプログラムが複雑になり過ぎたため、1回で処理できるV字は一つだけと妥協しました。この記事で挙げた例では1コマンドで1文字のものばかりです。これでも実用上の支障はなさそうです。
ここで紹介したローカル関数の引数は、点座標の指定方法が [x1 y1], [x2 y2] となっています。これは arrow3 でも同様です。しかし、MATLAB オリジナルの plot や annotation コマンドでは [x1 x2], [y1 y2] 方式をとっています。主軸を描くときとV字を描くときで座標の表現方法が異なるのは勘違いしやすくて気になります。そのつど自由にカスタマイズできるローカル関数ですから、ご利用の際にはお好みの方式に作り替えてください。
プログラム
図2の描画用プログラム
提案したローカル関数はプログラムの末尾にあります(ほぼ 300 行目以降)。(余談ですが、MATLAB の最新バージョン R2024a では、末尾以外の位置にもローカル関数を記述できるようになったようです)
矢印の描画には直接の影響はありませんが、このプログラムでは多画面表示用に 私製のユーザー定義関数(make_axes_tidily())も使用しています。しかし、プログラムの流れを追うだけであれば、「axes(hax(n))」を「figure(n)」と読み替えていただくだけで十分です。
% arrow_test02.m
% 矢印用のローカル関数の利用例の図を作成
clear
close all
% 多画面の figure を準備
[hax,hsp,h_number] = make_axes_tidily ...
('A4','land',[2 3],[85 85/1.2679],[30 27 15 10]);
delete(h_number)
% =============================================
% 二次元矢印( plot_arrow2d() の直線への適用 )
axes(hax(1));
axis equal
axis([[-1 1]*12.68 [-1 1]*10]/2);
hold on
% 放射光
p0=[-1.4 0]; % 放射の中心座標
Lo=4.2; % 放射光の上限枠
Li=2.5; % 〃 の下限枠
k=tan(30*pi/180);
Kx=[1 1 k 0 -k -1 -1 -1 -k 0 k 1]; % 放射光の向き
Ky=[0 k 1 1 1 k 0 -k -1 -1 -1 -k];
Cr=[0 4 0 0 0 4 3 0 4 0 0 0]/4; % 私製カラーマップ
Cg=[0 0 3 0 4 0 3 0 0 3 0 4]/4;
Cb=[0 0 0 4 4 4 0 0 0 0 4 4]/4;
xi=Li*Kx+p0(1); % 放射光の根元の座標
yi=Li*Ky+p0(2);
xo=Lo*Kx+p0(1); % 放射光の先端の座標
yo=Lo*Ky+p0(2);
for n=1:length(Kx)
plot([xi(n) xo(n)],[yi(n) yo(n)],'k'); % 主軸の線
% 矢印のV字
hv=plot_arrow2d([xi(n) yi(n)],[xo(n) yo(n)],10+80*n/12,1);
hv.LineWidth=0.5+3*n/12;
hv.Color=[Cr(n) Cg(n) Cb(n)];
end
% 曲尺セット
xl=linspace(-1.8,1.8,6)+p0(1);
yl=linspace(-1.8,1.8,6)+p0(2);
plot(xl,yl,'k');
for n=1:length(xl)-1
% 矢印のV字
hv=plot_arrow2d([xl(n) yl(n)],[xl(n+1) yl(n+1)],90,3.6*n/5);
hv.LineWidth=0.5+3*n/5;
hv.Color=[Cr(n) Cg(n) Cb(n)];
end
% ブラシ
yl=linspace(-3.5,3.5,21);
xl=4.5+0*yl;
plot(xl,yl,'k');
for n=1:length(xl)-2
% 矢印のV字
hv=plot_arrow2d([xl(n) yl(n)],[xl(n+1) yl(n+1)],360*n/20,1.2);
hv.LineWidth=1;
hv.Color=[Cr(mod(n-1,12)+1) Cg(mod(n-1,12)+1) Cb(mod(n-1,12)+1)];
end
title('A 二次元矢印(直線に適用)','FontSize',13);
% =============================================
% 二次元矢印( plot_arrow2d() の曲線への適用 )
axes(hax(2));
axis equal
axis([-6.35 6.35 -5 5]);
hold on
% 直線V字の表現力の限界を例示
ceny=linspace(-6.3,1,7);
R=3;
th=linspace(pi/4,pi/2,16);
for n=1:length(ceny)
x=R*cos(th)-5.5; y=R*sin(th)+ceny(n);
plot(x,y,'k','LineWidth',0.5);
% 矢印のV字
hv=plot_arrow2d([x(end-n) y(end-n)],[x(end) y(end)],30,1);
hv.LineWidth=1.5;
hv.Color='#aaa';
end
% 円弧V字の有用性を例示
p0=[1.5 0];
R=[2:4];
%th=linspace(0,2*pi/5,20);
th=linspace(0,2*pi/5,60);
for n=1:length(R);
for m=1:4
% 円弧
x=R(n)*cos(th+(m-1)*pi/2)+p0(1);
y=R(n)*sin(th+(m-1)*pi/2)+p0(2);
plot(x,y,'k');
% 矢印のV字
ha=plot_arrow2d([x(end-1) y(end-1)],[x(end) y(end)],30,1,R(n));
ha.LineWidth=1.5;
ha.Color=[Cr(n+1) Cg(n+1) Cb(n+1)];
hb=plot_arrow2d([x(2) y(2)],[x(1) y(1)],30,1,-R(n));
hb.LineWidth=1.5;
hb.Color=[Cr(n+1) Cg(n+1) Cb(n+1)];
end
end
title('B 二次元矢印(曲線に適用)','FontSize',13);
% =============================================
% 二次元矢印( annotation の利用 )
axes(hax(3));
% 往復電線路周りの磁界
x=[-10:2:10];
y=[-8:2:8];
[X,Y]=meshgrid(x,y);
d=8;
U1=Y.*(1./((X-d/2).^2+Y.^2));
V1=-(X-d/2)./((X-d/2).^2+Y.^2);
U2=-Y.*(1./((X+d/2).^2+Y.^2));
V2=(X+d/2)./((X+d/2).^2+Y.^2);
U=U1+U2; V=V1+V2; % 磁界のベクトル
L=sqrt(U.^2+V.^2); % 磁界の強さ
U0=U./L; V0=V./L; % 磁界の向きの単位ベクトル
% 磁界の強さの諧調分け(カラーマップ用のインデックス nc)
Lmax=max(max(L));
Lmin=min(min(L));
nc=floor(63.99*(L-Lmin)/(Lmax-Lmin))+1;
% 矢印の回転の中心点を軸の根元から軸の中央に変更
r=0.8; % 矢印の長さの半分
A=atan2(V,U); % 磁界ベクトルの傾き角度
X1=X+r*cos(A+pi); % 磁界ベクトルの根元の座標
Y1=Y+r*sin(A+pi);
X2=X+r*cos(A); % 磁界ベクトルの先端の座標
Y2=Y+r*sin(A);
axis equal
axis([[-9 9]*1.2679 [-9 9]]);
hold on
cmap=jet; % カラーマップとして jet を使用
for l=1:size(X,1)
for c=1:size(X,2)
% axes の axis 座標から figure の normalized 座標に変換
[x1_2,y1_2]=axe2fig(gca,[X1(l,c) X2(l,c)],[Y1(l,c) Y2(l,c)]);
if ~(isnan(x1_2) | isnan(y1_2))
annotation('arrow',x1_2,y1_2,'LineWidth',1, ...
'Color',cmap(nc(l,c),:));
end
end
end
text(4,0,'$$\otimes$$','FontSize',16,'Interpreter','latex', ...
'HorizontalAlign','center','VerticalAlign','middle');
text(-4,0,'$$\odot$$','FontSize',16,'Interpreter','latex', ...
'HorizontalAlign','center','VerticalAlign','middle');
title('C 二次元矢印(annotation の利用)','FontSize',13);
% =============================================
% 三次元矢印( plot_arrow3d() の直線への適用 )
axes(hax(4));
axis equal
axis([0 6 0 10 0 6]);
hold on
p1=[5 0 0];
p2=[0 9 0];
p3=[0 0 5];
fill3([p1(1) p2(1) p3(1)], ...
[p1(2) p2(2) p3(2)], ...
[p1(3) p2(3) p3(3)],[1 1 1]*0.95);
% 3点の座標から平面の式を求める
[a,b,c,d]=find_plane_const(p1,p2,p3);
nor=[a b c];
q1=[3 0.5];
q2=[3 3];
q3=[0.5 3];
q1=[q1 -(dot(q1,[a b])+d)/c];
q2=[q2 -(dot(q2,[a b])+d)/c];
q3=[q3 -(dot(q3,[a b])+d)/c];
q4=q1+(q2-q1)+(q3-q1);
% 主軸の描画
plot3([q1(1) q2(1)],[q1(2) q2(2)],[q1(3) q2(3)],'r','LineWidth',1.5)
% V字の描画
h=plot_arrow3d(q1,q2,40,1,nor);
h.Color='r';
h.LineWidth=1.5;
plot3([q1(1) q3(1)],[q1(2) q3(2)],[q1(3) q3(3)], ...
'Color','#0a0','LineWidth',1.5)
h=plot_arrow3d(q1,q3,40,1,nor);
h.Color='#0a0';
h.LineWidth=1.5;
plot3([q1(1) q4(1)],[q1(2) q4(2)],[q1(3) q4(3)],'b','LineWidth',1.5)
h=plot_arrow3d(q1,q4,40,1,nor);
h.Color='b';
h.LineWidth=1.5;
plot3([q2(1) q4(1)],[q2(2) q4(2)],[q2(3) q4(3)],'k');
plot3([q3(1) q4(1)],[q3(2) q4(2)],[q3(3) q4(3)],'k');
r1=[5 9 0];
r2=[5 3 0];
r3=[1 9 0];
r4=[5 0 5];
r5=[1 0 5];
r6=[5 0 1];
r7=[0 9 5];
r8=[0 2 5];
r9=[0 9 1];
% 主軸の描画
plot3([r1(1) r2(1)],[r1(2) r2(2)],[r1(3) r2(3)],'r','LineWidth',1.5);
% V字の描画
h=plot_arrow3d(r1,r2,40,1,[0 0 1]);
h.Color='r';
h.LineWidth=1.5;
plot3([r1(1) r3(1)],[r1(2) r3(2)],[r1(3) r3(3)],'r','LineWidth',1.5);
h=plot_arrow3d(r1,r3,40,1,[0 0 1]);
h.Color='r';
h.LineWidth=1.5;
plot3([r4(1) r5(1)],[r4(2) r5(2)],[r4(3) r5(3)], ...
'Color','#0a0','LineWidth',1.5);
h=plot_arrow3d(r4,r5,40,1,[0 1 0]);
h.Color='#0a0';
h.LineWidth=1.5;
plot3([r4(1) r6(1)],[r4(2) r6(2)],[r4(3) r6(3)], ...
'Color','#0a0','LineWidth',1.5);
h=plot_arrow3d(r4,r6,40,1,[0 1 0]);
h.Color='#0a0';
h.LineWidth=1.5;
plot3([r7(1) r8(1)],[r7(2) r8(2)],[r7(3) r8(3)],'b','LineWidth',1.5);
h=plot_arrow3d(r7,r8,40,1,[1 0 0]);
h.Color='b';
h.LineWidth=1.5;
plot3([r7(1) r9(1)],[r7(2) r9(2)],[r7(3) r9(3)],'b','LineWidth',1.5);
h=plot_arrow3d(r7,r9,40,1,[1 0 0]);
h.Color='b';
h.LineWidth=1.5;
grid on
view([138 17]);
xlabel('x');
ylabel('y');
zlabel('z');
ax=gca;
ax.CameraViewAngle=7.7; % 図を大きめに拡大
title('D 三次元矢印(直線に適用)','FontSize',13);
% =============================================
% 三次元矢印( plot_arrow3d() の曲線への適用1 )
axes(hax(5));
axis equal
axis([0 6 0 10 0 6]);
hold on
% 螺旋
R=2.5;
th=linspace(0,4*2*pi,4*72+1);
x=R*cos(th)+3;
y=9*th/(th(end));
z=R*sin(th)+3;
plot3(x,y,z,'k')
for n=8:6:length(th)-1
% V字の描画
h=plot_arrow3d([x(n) y(n) z(n)],[x(n+2) y(n+2) z(n+2)], ...
60,0.6,[cos(th(n+1)) 0 sin(th(n+1))]);
h.LineWidth=1.5;
h.Color='b';
end
grid on
view([138 17]);
xlabel('x');
ylabel('y');
zlabel('z');
ax=gca;
ax.CameraViewAngle=7.7; % 図を大きめに拡大
text(0,-1.5,5.2,' V字の描画面 = 円筒面','FontSize',10);
title('E 三次元矢印(曲線に適用)','FontSize',13);
% =============================================
% 三次元矢印( plot_arrow3d() の曲線への適用2 )
axes(hax(6));
axis equal
axis([0 6 0 10 0 6]);
hold on
% 螺旋
R=2.5;
th=linspace(0,4*2*pi,4*72+1);
x=R*cos(th)+3;
y=9*th/(th(end));
z=R*sin(th)+3;
plot3(x,y,z,'k')
for n=8:6:length(th)-1
% V字描画面(螺旋面)の法線の取得
[a,b,c,~]=find_plane_const([x(n) y(n) z(n)], ...
[x(n+1) y(n+1) z(n+1)],[3 y(n+1) 3]);
% V字の描画
h=plot_arrow3d([x(n) y(n) z(n)],[x(n+1) y(n+1) z(n+1)], ...
60,0.6,-[a b c],-2.5,3);
h.LineWidth=1.5;
h.Color='b';
end
grid on
view([138 17]);
xlabel('x');
ylabel('y');
zlabel('z');
ax=gca;
ax.CameraViewAngle=7.7;
text(0,-1.5,5.2,' V字の描画面 = 螺旋面','FontSize',10);
title('F 三次元矢印(曲線に適用)','FontSize',13);
% ===============================
% ■■■ ローカル関数群 ■■■
% ===============================
% ========================================================
% ========================================================
% 矢印の頭のV字の描画(二次元グラフ用。1コマンドで多V字処理可能)
function [h_arw]=plot_arrow2d(xy1,xy2,ang,leng,rad,rev)
% 【入力】
% xy1 : 主軸上に存在する任意の1点のx,y座標(n行2列の行列)
% n: 1コマンドで同時に描くV字の個数
% xy2 : 矢印の先端のx,y座標(n行2列の行列)
% ang : V字の両翼間の開き角度[度]
% leng : V字の両翼の長さ
% 【入力(任意)】
% rad : 主軸の曲率半径(+/- : 左/右へ曲がるカーブ)
% rev : V字中心線の傾き角度の補正量[度](rev>0)
% 【出力】
% h_arw : 描かれたV字図形のハンドル(n行1列のLine配列)
ang=ang*pi/180;
if nargin>=5 % 曲率半径 rad の入力があったときの処理。
if nargin==6 % さらに、V字の傾き角度の補正を指示されたとき。
threv=sign(rad)*rev*pi/180;
else
threv=0;
end
th0=atan2(xy2(:,2)-xy1(:,2), ...
xy2(:,1)-xy1(:,1))+sign(rad)*pi/2+threv;
R=abs(rad);
cen1=R*[cos(th0-ang/2) sin(th0-ang/2)]+xy2; % 円弧1の中心座標
cen2=R*[cos(th0+ang/2) sin(th0+ang/2)]+xy2; % 円弧2の中心座標
th=linspace(0,leng/rad,5); % 弧長バラメータ/半径
x1=R*cos(-pi+th0-ang/2-fliplr(th))+cen1(1); % 円弧1の折線座標
y1=R*sin(-pi+th0-ang/2-fliplr(th))+cen1(2);
x2=R*cos(-pi+th0+ang/2-th)+cen2(1); % 円弧2の折線座標
y2=R*sin(-pi+th0+ang/2-th)+cen2(2);
x=[x1 x2]; y=[y1 y2];
h_arw=plot(x,y,'k');
else % 曲率半径 rad の入力が無いときの処理
th0=atan2(xy2(:,2)-xy1(:,2),xy2(:,1)-xy1(:,1))+pi;
x0=xy2(:,1); y0=xy2(:,2);
x1=leng*cos(th0-ang/2)+x0; y1=leng*sin(th0-ang/2)+y0;
x2=leng*cos(th0+ang/2)+x0; y2=leng*sin(th0+ang/2)+y0;
h_arw=plot([x1 x0 x2]',[y1 y0 y2]','k');
end
end
% ========================================================
% ========================================================
% 矢印の頭のV字の描画(三次元グラフ用。
% 1コマンドで処理できるV字は1つのみ)
function [h_arw]=plot_arrow3d(xyz1,xyz2,ang,leng,nor,rad,rev)
% 【入力】
% xyz1 : 主軸上に存在する任意の1点のx,y,z座標
% (3要素の行ベクトル)
% xyz2 : 矢印の先端のx,y,z座標(3要素の行ベクトル)
% ang : V字の両翼間の角度[度]
% leng : V字の両翼の長さ
% nor : V字描画面の法線のx,y,z座標(3要素の行ベクトル)
% 【入力(任意)】
% rad : 主軸の曲率半径
% (+/- : 法線側から見て左/右へ曲がるカーブ)
% rev : V字中心線の傾き角度の補正量[度](rev>0)
% 【出力】
% h_arw : 描かれたV字図形のハンドル
ang=ang*pi/180;
nor_a=(xyz2-xyz1)/norm(xyz2-xyz1); % 主軸方向の単位ベクトル
% ===================
% 回転前のV字の原図(xy面上で先端を[0 0]に置いてy軸の正方向向き)
if nargin>=6 % 曲率半径 rad の入力があったときの処理。
if nargin==7 % さらに、V字の傾き角度の補正を指示されたとき。
threv=sign(rad)*rev*pi/180;
else
threv=0;
end
th0=sign(rad)*pi/2+pi/2+threv;
R=abs(rad);
cen1=R*[cos(th0-ang/2) sin(th0-ang/2)]; % 円弧1の中心座標
cen2=R*[cos(th0+ang/2) sin(th0+ang/2)]; % 円弧2の中心座標
th=linspace(0,leng/rad,5); % 弧長バラメータ/半径
x1=R*cos(-pi+th0-ang/2-fliplr(th))+cen1(1); % 円弧1の折線座標
y1=R*sin(-pi+th0-ang/2-fliplr(th))+cen1(2);
x2=R*cos(-pi+th0+ang/2-th)+cen2(1); % 円弧2の折線座標
y2=R*sin(-pi+th0+ang/2-th)+cen2(2);
x=[x1 x2]; y=[y1 y2]; z=x*0;
else % 曲率半径 rad の入力が無いときの処理
x=[-1 0 1]*leng*sin(ang/2);
y=-[1 0 1]*leng*cos(ang/2);
z=x*0;
end
nor_z=[0 0 1]; % V字の原図面の法線 [0 0 1]
% ===================
% 1回目の回転
if norm(nor_z-nor)<1e-6 % 【両法線ベクトルが殆ど一致しているとき】
p2=[x;y;z]'; % 点群を縦方向に並べ替え
nor_t=[0 1 0]; % V字の主軸方向のベクトル(+y方向)
elseif norm(nor_z+nor)<1e-6 % 【両法線ベクトルが逆向きで殆ど相殺】
p2=[x;-y;z]'; % yだけを反転し点群を縦方向に並べ替え
nor_t=[0 -1 0]; % V字の主軸方向のベクトル(-y方向)
else % 【両法線ベクトル間に有意差があるとき】
% 法線 nor_z を指定法線 nor に一致させるための回転中心軸と
% 回転角度を求める。スカラー積(sp)の正負で処理を分ける。
sp=dot(nor_z,nor); % 両ベクトルの角度差が90°以下で正。
if sp>=0 % 90°以下
axrot=cross(nor_z,nor); % 両者の外積をとり、回転中心軸を得る。
angrot=asin(norm(axrot)); % 一致させるために回転すべき角度。
else % 90°超
axrot=cross(nor_z,-nor); % 回転中心軸をsp>=0のときとは逆向きに。
angrot=asin(norm(axrot))+pi; % 一致させるために回転すべき角度。
end
% V字の原図を回転(主軸上の情報も1点だけ付加)
p2=rot_points_3d([0 0 0],axrot,[[0 -1 0];[x;y;z]'],angrot);
nor_t=[0 0 0]-p2(1,:); % 回転後のV字の主軸方向のベクトル
nor_t=nor_t/norm(nor_t) ; % 同上の単位ベクトル化
p2(1,:)=[]; % 用済みの付加主軸情報を削除
end
% ===================
% 2回目の回転
% nor_a ベクトルの【1回目の回転後の描画面】への投影ベクトルを
% 単位化したベクトル nor_b を求める。
% ローカル関数の呼び出し
[x2,y2,z2,~]=intsec_Plane_and_PerpLine(nor(1),nor(2),nor(3),0, ...
nor_a(1),nor_a(2),nor_a(3));
nor_b=[x2 y2 z2]/norm([x2 y2 z2]);
if norm(nor_t-nor_b)<1e-6 % 【両主軸方向単位ベクトルが殆ど一致】
p2=p2; % 何もせず
elseif norm(nor_t+nor_b)<1e-6 % 【両主軸方向単位ベクトルが
% 逆向きで殆ど相殺】
p2=-p2; % ベクトルを反転
else % 【両主軸方向単位ベクトル間に有意差があるとき】
% nor_t をnor_b に一致させるための回転中心軸と回転角度を
% 求める。スカラー積(sp)の正負で処理を分ける。
sp=dot(nor_t,nor_b); % 両ベクトルの角度差が90°以下で正。
if sp>=0 % 90°以下
axrot=cross(nor_t,nor_b); % 両者の外積をとり、回転中心軸を得る。
angrot=asin(norm(axrot)); % 一致させるために回転すべき角度。
else % 90°超
axrot=cross(nor_t,-nor_b); % 回転中心軸をsp>=0のときとは逆向きに。
angrot=asin(norm(axrot))+pi; % 一致させるために回転すべき角度。
end
p2=rot_points_3d([0 0 0],axrot,p2,angrot);
end
p2=p2+xyz2; % V字の頂点を指定点まで平行移動
% V字の描画
h_arw=plot3(p2(:,1),p2(:,2),p2(:,3),'k');
end
% ========================================================
% ========================================================
% 多点群を一括して三次元回転させる関数
function [p2]=rot_points_3d(v00,v0,p1,ang)
%【入力】
% v00: 回転軸ベクトルの始点の座標(1行3列の行ベクトル)
% v0: 回転軸ベクトルの向き
% (1行3列の行ベクトル。単位化されていなくても可)
% p1: 回転される前の点群の座標(多行3列の行列)
% ang: 回転角[rad]( v0の右ねじ方向が正。スカラー)
%
%【出力】
% p2: 回転された後の点群の座標(多行3列の行列)
p1t=p1'; % 点群の座標を転置して3行多列化。
nn=v0/norm(v0); % 回転軸ベクトルの単位化
n1=nn(1); n2=nn(2); n3=nn(3); % 回転軸ベクトルのx,y,z成分
sa=sin(ang);
ca=cos(ang);
ca1=1-ca; % 1-cos(ang)
% ロドリゲスの三次元回転行列
R=[n1^2*ca1+ca n1*n2*ca1-n3*sa n3*n1*ca1+n2*sa
n1*n2*ca1+n3*sa n2^2*ca1+ca n2*n3*ca1-n1*sa
n3*n1*ca1-n2*sa n2*n3*ca1+n1*sa n3^2*ca1+ca ];
p1t=p1t-v00'; % 回転ベクトルの始点が原点に来るように、
% 座標全体を平行移動する。
p2t=R*p1t; % v0を中心軸にして点群を回転させる。
p2t=p2t+v00'; % 回転前に行った平行移動を元に戻す。
p2=p2t'; % 転置して多行3列化したうえ、最終出力とする。
end
% ========================================================
% ========================================================
% axes の座標値を figure の normalized 単位に変換するローカル関数
function [x1_2,y1_2]=axe2fig(haxe,x1x2,y1y2)
% 【入力】
% haxe: 現在アクティブになっている axes のハンドル。
% 呼び出し側での引数は「gca」とすること。
% x1x2: axes 上の点の x座標群(点の数に相当する要素数の行ベクトル)
% y1y2: 〃 y 〃
% 【出力】
% x1_2: x1x2 を normalized 単位に変換後の行ベクトル
% y1_2: y1y2 〃
ap=haxe.Position;
al=ap(1); ab=ap(2); aw=ap(3); ah=ap(4);
area=axis(haxe);
xmin=area(1); xmax=area(2); ymin=area(3); ymax=area(4);
x1_2=aw*(x1x2-xmin)/(xmax-xmin)+al;
y1_2=ah*(y1y2-ymin)/(ymax-ymin)+ab;
end
% ========================================================
% ========================================================
% 3点の座標から それらを含む平面の式の係数を求めるローカル関数
function [a,b,c,d]=find_plane_const(xyz1,xyz2,xyz3)
% 【入力】
% xyz1,xyz2,xyz3:
% 3点の座標 [x1 y1 z1],[x2 y2 z2],[x3 y3 z3]。
% 3点は一直線上に並んでいないこと。
% 【出力】
% a,b,c,d:
% 平面の式 ax + by + cz + d = 0 の係数。
% [a b c] が法線の単位ベクトルになるように正規化済。
% ただし、逆向きの -[a b c] も同じく法線。意図に応じて
% 適切な方を選択。
p2=xyz2-xyz1; p3=xyz3-xyz1;
norx=cross(p2,p3);
nor=norx/norm(norx);
a=nor(1); b=nor(2); c=nor(3);
d=-dot(nor,xyz1);
end
% ========================================================
% ========================================================
% 【任意の点】から【任意の平面】への垂線が、その平面と交わる点の座標
function [x2,y2,z2,L]=intsec_Plane_and_PerpLine(a,b,c,d,x1,y1,z1)
% 【入力】
% a,b,c,d: 平面の式 ax + by + cz + d = 0 の係数。
% 正規化前の平面の法線は [a b c] と解釈される。
% x1,y1,z1: 任意の点の座標
% 【出力】
% x2,y2,z2: 平面上にできた交点の座標
% L: 垂線の長さ(法線側のとき +、反対側のとき -)
% 平面の式の係数の正規化
U=[a b c d]/norm([a b c]);
a=U(1); b=U(2); c=U(3); d=U(4);
% 交点の計算
M=[1 0 0 a
0 1 0 b
0 0 1 c
a b c 0];
V=inv(M)*[x1 y1 z1 -d]';
x2=V(1); y2=V(2); z2=V(3); L=V(4);
end
図1の描画用プログラム
紹介したローカル関数とは直接の関係はありませんが、参考までに添付しておきます。既述の多画面表示用のユーザー定義関数のほかに、MATLAB の File Exchange からダウンロードした Jeff Chang 氏と Tom Davis 氏による関数「arrow3」も使用しています。
% arrow_test01.m
% MATLAB に既存の矢印コマンドの応用図を作成
clear
close all
% 多画面の figure を準備
[hax,hsp,h_number] = make_axes_tidily ...
('A4','land',[2 3],[85 85/1.2679],[30 30 20 15]);
delete(h_number)
% ====================================
% quiver
axes(hax(1))
x=[-8:2:8];
y=[-8:2:8];
[X,Y]=meshgrid(x,y);
d=8;
U1=Y.*(1./((X-d/2).^2+Y.^2));
V1=-(X-d/2)./((X-d/2).^2+Y.^2);
U2=-Y.*(1./((X+d/2).^2+Y.^2));
V2=(X+d/2)./((X+d/2).^2+Y.^2);
U=U1+U2;
V=V1+V2;
quiver(X,Y,U,V,'LineWidth',1);
hold on
text(4,0,'$$\otimes$$','FontSize',16,'Interpreter','latex', ...
'HorizontalAlign','center','VerticalAlign','middle');
text(-4,0,'$$\odot$$','FontSize',16,'Interpreter','latex', ...
'HorizontalAlign','center','VerticalAlign','middle');
axis equal
title('quiver','FontSize',14);
% ====================================
% quiver3
axes(hax(2))
x=[-6:2:6];
y=[-6:2:6];
z=[-6:2:6];
d=8;
[X,Y,Z]=meshgrid(x,y,z);
U1=(X-d/2)./(((X-d/2).^2+Y.^2+Z.^2).^(3/2));
V1=Y./(((X-d/2).^2+Y.^2+Z.^2).^(3/2));
W1=Z./(((X-d/2).^2+Y.^2+Z.^2).^(3/2));
U2=-(X+d/2)./(((X+d/2).^2+Y.^2+Z.^2).^(3/2));
V2=-Y./(((X+d/2).^2+Y.^2+Z.^2).^(3/2));
W2=-Z./(((X+d/2).^2+Y.^2+Z.^2).^(3/2));
U=U1+U2;
V=V1+V2;
W=W1+W2;
quiver3(X,Y,Z,U,V,W,'LineWidth',1);
hold on
text(-d/2,0,0,'$$\ominus$$','FontSize',16,'Interpreter','latex', ...
'HorizontalAlign','center','VerticalAlign','middle');
text(d/2,0,0,'$$\oplus$$','FontSize',16,'Interpreter','latex', ...
'HorizontalAlign','center','VerticalAlign','middle');
axis equal
title('quiver3','FontSize',14);
% ====================================
% feather
axes(hax(3))
theta = -pi/2:pi/16:pi/2;
r=5*(1-(theta+pi/2)/pi);
[u,v] = pol2cart(theta,r);
hfe=feather(u,v);
for n=1:length(hfe)
hfe(n).LineWidth=1;
end
axis equal
title('feather','FontSize',14);
% ====================================
% compass
axes(hax(4))
theta = 0:pi/12:2*pi;
r = 1*(1+theta/(2*pi));
[u,v] = pol2cart(theta,r);
hco=compass(u,v);
for n=1:length(hco)
hco(n).LineWidth=1;
end
title('compass','FontSize',14);
% ====================================
% annotation
axes(hax(5))
%ax=axes;
axis([0 10 0 10]);
hold on
grid on
plot(5,6,'or','LineWidth',1);
[x,y]=axe2fig(gca,[2 8],[8 2]);
annotation('arrow',x,y,'LineWidth',1);
[x,y]=axe2fig(gca,[2 5],[2 8]);
annotation('doublearrow',x,y,'LineWidth',1);
[x,y]=axe2fig(gca,[7 5],[7 6]);
annotation('textarrow',x,y,'String','Red Marker','LineWidth',1);
text(6,4,'arrow','FontSize',12,'HorizontalAlign','center');
text(3,4,'doublearrow','FontSize',12,'HorizontalAlign','center');
text(8,8,'textarrow','FontSize',12,'HorizontalAlign','center');
title('annotation','FontSize',14);
% ====================================
% arrow3
axes(hax(6))
th=linspace(0,2*pi,11);
th(end)=[];
arrow3(zeros(10,3),[10*cos(th') 10*sin(th') th'*0+9],'x1',2,4,[],0.95);
hold on
arrow3(zeros(10,3),[10*cos(th') 10*sin(th') th'*0-9],'x1',2,4,[],0.95);
light('Position',[-20 -20 50],'Style','local')
light('Position',[60,60,60]), lighting gouraud
grid on
axis equal
axis([-10 10 -10 10 -10 10]);
title('arrow3(非純正)','FontSize',14);
% ========================================================
% ========================================================
% axes の座標値を figure の normalized 単位に変換するローカル関数
function [x1_2,y1_2]=axe2fig(haxe,x1x2,y1y2)
% 【入力】
% haxe: 現在アクティブになっている axes のハンドル。
% 呼び出し側での引数は「gca」とすること。
% x1x2: axes 上の点の x座標群(点の数に相当する要素数の行ベクトル)
% y1y2: 〃 y 〃
% 【出力】
% x1_2: x1x2 を normalized 単位に変換後の行ベクトル
% y1_2: y1y2 〃
ap=haxe.Position;
al=ap(1); ab=ap(2); aw=ap(3); ah=ap(4);
area=axis(haxe);
xmin=area(1); xmax=area(2); ymin=area(3); ymax=area(4);
x1_2=aw*(x1x2-xmin)/(xmax-xmin)+al;
y1_2=ah*(y1y2-ymin)/(ymax-ymin)+ab;
end