なぜ書こうと思ったか
私は自己学習で統計学を学んでおりますが、実務的にプログラムを用いるのではなく、主に数学を使って理論的に証明したりする方がメインです。
そこで、実務でも生かせるように、Pythonで勉強したいなと思っているのですが、このあたりの話をPythonで解説している本や記事ってあまり多くないなと思いました。「R」で解説しているものがとても多いです。(特に時系列系は・・)
Rは確かに便利だけれど、Rのラーニングコストはかけたくない。Pythonで何とかできないものか・・・
そう思って調べてみたので、ここに書いていきます。
Scipyやstatsmodelsを使おう
scipyには高度な統計的処理のためのツールが多く実装されています。
scipy.statsのドキュメントを見てみましょう。
This module contains a large number of probability distributions, summary and frequency statistics, correlation functions and statistical tests, masked statistics, kernel density estimation, quasi-Monte Carlo functionality, and more.
Statistics is a very large area, and there are topics that are out of scope for SciPy and are covered by other packages. Some of the most important ones are:
直訳: このモジュールは、確率分布、要約統計、度数統計、相関のための関数や、統計的検定、masked statistics、カーネル密度推定、モンテカルロの機能、その他多くのモジュールを取り揃えております。
統計学は非常に広い領域にわたり、scipyでは扱いきれないためほかのパッケージで扱われている領域もあります。
特に重要なのは、
- statsmodels: 回帰、線形モデル、時系列分析、scipy.statsでもカバーしているがそのさらに拡張された領域
- pandas: テーブルデータ、時系列処理機能、ほかの統計言語へのインタフェース。
- PyMC3: ベイズ統計モデル、確率的機械学習
- scikit-learn: 分類、回帰、モデル選択
- rpy2: Rへの橋掛けになるPython
など、こんなにたくさんのパッケージが開発されているんですね。
仮説検定をしよう
では、今回はscipyを使って仮説検定をしてみましょう。
仮説検定とは、次のような手順で進めます。
- データ群 $\mathscr{D}$ を観測する。(収穫したジャガイモ1つずつの重量や、生後2年後に測ったシカの体重など。時系列であれば1時間おきの株の値動きや、毎日の14時の気温など)
- データ群 $\mathscr{D}$ について、帰無仮説 $H_0$を立てる。$H_0$を否定する対立仮説$H_1$を立てる。
- 有意水準$\alpha$を設定する。
- $H_0$が成り立っていると仮定して、データ群から検定統計量 $t=f(\mathscr{D})$ を求める。
- $H_0$が成り立っていると仮定した場合に、検定統計量 $f$ が、先ほど求めた値になる確率 $P(f=t)$ (p値)を調べる。
- $P(f=t)$の値によって、帰無仮説$H_0$を採択または棄却する。
例題1
とあるA駅とB駅の日々の乗降客数を、曜日ごとに集計したデータがあるとします(私がでたらめに作りました)。
| 駅\曜日 | 日 | 月 | 火 | 水 | 木 | 金 | 土 |
|---|---|---|---|---|---|---|---|
| A駅 | 130 | 91 | 110 | 99 | 102 | 88 | 145 |
| B駅 | 5242 | 7213 | 8122 | 7559 | 6999 | 7730 | 6401 |
このデータから、「2つの駅の間には、曜日による乗降客数の違いがある」といえるかどうか確かめましょう。
(まあ、明らかにA駅は平日がすくなく、B駅は平日が多いので明らかといえば明らかですが・・・)
1. データの準備
>> df_stations
A B
日 130 5242
月 91 7213
火 110 8122
水 99 7559
木 102 6999
金 88 7730
土 145 6401
2. 帰無仮説を立てる
帰無仮説は、普通は「成り立ってしまったら面白くない」仮説を設定します。
帰無仮説$H_0$は「2つの駅の違いは、曜日による乗降客数とは関係ない」とします。
対立仮説$H_1$は「2つの駅の違いは、曜日による乗降客数とは関係ないとは言えない」となります。
3. 有意水準を設定する
よく用いられる$\alpha = 0.05$を、今回は採用します。(5%有意)
4. 帰無仮説が成り立つ仮定の下、検定統計量を求める。
今回の場合「独立性の検定」なので、カイ2乗統計量$\chi^2$を計算します。
カイ2乗統計量については、こちらを見るとわかりやすいでしょう。
このように分割表(上記のような2変数の関係を表した表)を用いた場合の独立性検定を行うには、
scipy.stats.chi2_contingencyを用います。contingency tableとは、「分割表」の意味です。
>> from scipy.stats import chi2_contingency
>> chi2, p, dof, expected = chi2_contingency(df_stations)
>> chi2 # カイ2乗統計量
# 66.3978492422048
>> p # p値
# 2.234890796242267e-12 めちゃ低い!
>> dof # 自由度
# 6 (= (7-1) * (2-1))
>> expected # 帰無仮説が成り立つ場合の理想的なデータ
# array([[ 82.14067278, 5289.85932722],
# [ 111.68195719, 7192.31804281],
# [ 125.87155963, 8106.12844037],
# [ 117.09480122, 7540.90519878],
# [ 108.57798165, 6992.42201835],
# [ 119.5412844 , 7698.4587156 ],
# [ 100.09174312, 6445.90825688]])
5. p値を求める。
これは先ほどのchi2_contingencyの戻り値の2つ目の値です。
解釈としては、$H_0$が成り立つ(=2つの駅の違いは、曜日による乗降客数とは関係ない)場合、このようなデータ分布になる確率は0.000000000002234...という値になり、「非常に発生しにくい」データであることになります。
6. 帰無仮説を棄却するか採択する。
今回の有意水準は$\alpha=0.05$であり、p値はこれより小さいので、帰無仮説は棄却され、対立仮説$H_1$を採択することになります。つまり「無関係ではない」ということになりますね。
>> p < 0.05
# True
例題2
時系列データを解析する場合を考えます。
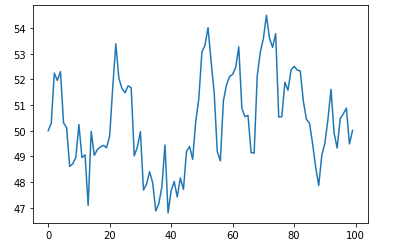
次のデータは、ある架空の国「hogefuga王国」の通貨「hogefugaドル」の、日本円に対する為替レートの遷移です(今回もでたらめに生成してます)。
ちなみにデータはこんな感じ。
array([50. , 50.29018729, 52.24746262, 51.95948449, 52.30537823,
50.30824405, 50.12172432, 48.60905031, 48.70921254, 48.95964847,
50.24004133, 48.95208361, 49.06108964, 47.0873981 , 49.97352252,
49.04393404, 49.2635312 , 49.37430142, 49.42896761, 49.3379284 ,
49.79211113, 51.6852042 , 53.38809255, 52.04678404, 51.64397987,
51.47967125, 51.75186846, 51.67725345, 49.01984971, 49.35769732,
49.96173114, 47.68886876, 47.91758683, 48.40041588, 47.9655245 ,
46.87199508, 47.15860814, 47.83286584, 49.44340886, 46.79513279,
47.65791787, 48.02065927, 47.41468155, 48.16131616, 47.70832925,
49.2027023 , 49.38443245, 48.88218994, 50.36831835, 51.24837892,
53.06043172, 53.33838394, 54.01792043, 52.70299847, 51.48739893,
49.19198816, 48.82556554, 51.17004644, 51.78406776, 52.11195467,
52.19841999, 52.47212234, 53.27458889, 50.88217615, 50.54862287,
50.59606089, 49.15094123, 49.12637222, 52.13693472, 53.06757104,
53.59809557, 54.50360915, 53.60386972, 53.25087725, 53.78453896,
50.53479559, 50.54783952, 51.89105923, 51.57822674, 52.36594804,
52.51303693, 52.36564884, 52.32803107, 51.14820464, 50.44996359,
50.29173659, 49.50658412, 48.58663957, 47.86515488, 49.038624 ,
49.5151172 , 50.43601702, 51.61553717, 49.91537236, 49.32696871,
50.48156464, 50.65876206, 50.87989071, 49.48715774, 50.01020616])
確かめたいこと
この国の通貨の遷移がAR(1)モデルであると仮定して、「定常仮定」かどうかを検定によって求めます。
AR(1)モデルとは、ある時刻$t$における値$y_t$が、
$y_t = a_1y_{t-1} + c + \epsilon_{t}$ ($c$: 定数、 $\epsilon \sim N(0, \sigma^2)$ : かく乱項 ・・・(*)
という関係であらわされる時系列モデルで、$|a_1| < 1$となるモデルを「定常過程」と呼びます。
上記のデータは$y_0=50, a_1 = 0.86, c=7, \sigma=1$として生成しました。
帰無仮説
帰無仮説$H_0$は、「hogefugaドル円の遷移は定常過程ではない」
対立仮説$H_1$は、「hogefugaドル円の遷移は定常過程である」
となります。
帰無仮説の仮定の下、検定統計量を求める。
時系列データが定常過程であるかどうかを確かめるには、ADF検定(拡張Dickey-Fuller検定)を用います。
Pythonで実行するにはstatsmodelsのadfullerを用います。
- statsmodels.tsa.stattools.adfuller: https://www.statsmodels.org/stable/generated/statsmodels.tsa.stattools.adfuller.html#statsmodels.tsa.stattools.adfuller
from stattools.tsa.stattools import adfuller
adf_ctt, p_ctt, _, _, _, _ = adfuller(y, regression="ctt") # 2次トレンド,定数項ありと仮定した場合の検定
adf_ct, p_ct, _, _, _, _ = adfuller(y, regression="ct") # 1次トレンド,定数項ありと仮定した場合の検定
adf_c, p_c, _, _, _, _ = adfuller(y, regression="c") # 定数項ありと仮定した場合の検定
adf_nc, p_nc, _, _, _, _ = adfuller(y, regression="nc") # 定数項なしと仮定した場合の検定
※ n次トレンド: (*)に$t^n$の定数倍(n次トレンド項)が加えられる場合
結果を見てみると
>> p_ctt
# 0.13359927561492813
>> p_ct
# 0.0456032572749854
>> p_c
# 0.015698845576062978
>> p_nc
# 0.645196170543882
となっており、有意水準$\alpha = 0.05$では、「1次トレンドと定数項を仮定した場合」と、「定数項のみを仮定した場合」に、
「hogefugaドルの為替レートは定常過程である」といえそうです。
有効活用するには?
上記の例で、とりあえずpythonでも統計量を簡単に求める方法があることは知ることができました。
「numpyやscipyでごにょごにょやらなアカンのか、、、」という不安は消え去りました。
ということは、あと必要なのは「どの場合にどんな検定を用いるのか」という知識です。
この辺りは、やっぱり統計学の教科書等で勉強していくしかないでしょうね。
がんばる!!!