Python3 を子供に教えるためにオセロを作ってみた（６）最終回

オセロクラスについて解説していきましょう　その３

「関数に渡された X と Y の隣のコマと、その隣のコマを調べる」関数

　さてさて、最も難解かもしれませんが解説していきます。
　これから説明するオセロクラスの関数 ot_next_onepeace() は、**「関数に渡された X と Y の隣のコマと、その隣のコマを調べる」という機能の関数です。
　この言葉がとても重要になる関数です。もう１度言いますね。
　この関数が実行するのは「関数に渡された X と Y の隣のコマと、その隣のコマを調べる」だけです。
　仮にオセロ盤のマス目が100ｘ100の盤だったとしても、この関数が実行するのは「関数に渡された X と Y の隣のコマと、その隣のコマを調べる」**だけなのです。

なぜなら「自分が自分を呼び出す関数（再帰関数）」だから！

　少なからずコマを置けると判断した場合、ひっくり返せる方角を全てひっくり返していかないとなりません。そのためには、８方向に対してひっくり返しができるかどうか？、どこまでひっくり返せるか？を考えなければなりませんよね。

　この関数では、例えば●を特定の座標に置いた場合、その置かれたX座標とY座標、それに調べたい方向のキー文字を引数に渡して、**「関数に渡された X と Y の隣のコマと、その隣のコマを調べる」**のです。（しつこいですね！）

　８方向の隣の座標を表す、ディクショナリ変数ot_directionのキーが三番目の引数として渡されます。'ul' や 'up' というキー文字列です。そのキー文字列に合致するタプル配列[0]にはX座標の隣の手を表す数値が入っています。左方向に探すのであれば-1が入っています。真上か真下なら0で、右方向であれば+1という具合です。同じようにタプル配列[1]にはY座標の隣の手を表す数値が入っています。このタプル配列[0]を nx という変数に、タプル配列[1]をnyという変数に格納します。ディクショナリ配列にアクセスする方式は、ot_direction[キー文字（３番目の引数）][タプル配列の添字]でアクセスします。このやり方を忘れないでくださいね。もしキーに対して値が１つしかなければ一次元配列と同じアクセス方式ot_direction[キー文字（３番目の引数）]でアクセスします。今回はキー文字列に対してタプル配列になっているので、二次元配列と同じアクセス方式になるというわけです。

        self.ot_direction = { 'ul' : ( -1 , -1 ) ,  # 左斜め上
                              'up' : (  0 , -1 ) ,  # 真上
                              'ur' : ( +1 , -1 ) ,  # 右斜め上
                              'lt' : ( -1 ,  0 ) ,  # 左
                              'rt' : ( +1 ,  0 ) ,  # 右
                              'dl' : ( -1 , +1 ) ,  # 左斜め下
                              'dn' : (  0 , +1 ) ,  # 真下
                              'dr' : ( +1 , +1 ) }  # 右斜め下

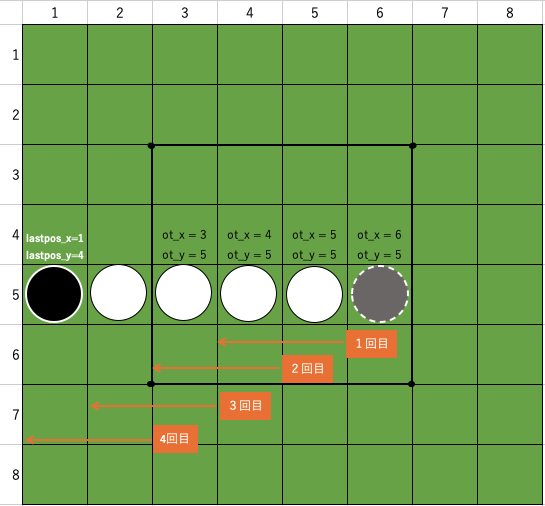
　この関数の１番目と２番目の引数には、コマを置いたX座標 ot_x と、Y座標 ot_y が渡されます。それに対して以下の nx と ny を加算することで、探す方向のコマが確定するわけです。その引数で渡されたX座標 ot_x と、Y座標 ot_yの隣と隣を調べたら、一個ずらしてまた自分の関数を呼びます。図にするとこんな感じです。

1. 1回目は X=6 , Y=5 の左隣のコマと、さらにその左隣のコマを調べます。（○と○ですね！！）
2. この関数は ot_x と ot_y で渡された値を1個ディクショナリ変数のタプル配列に入った数値の指示に従って1つずらして、再び自分の関数を呼びます。
3. 2回目に呼ばれた関数の引数は X=5 , Y=5 になっています。またそこから左隣のコマと、さらにその左隣のコマを調べます。（再び○と○ですね！！）
4. 再びこの関数は ot_x と ot_y で渡された値を1個ディクショナリ変数のタプル配列に入った数値の指示に従って1つずらして、再び自分の関数を呼びます。
5. 3回目に呼ばれた関数の引数は X=4 , Y=5 になっています。またそこから左隣のコマと、さらにその左隣のコマを調べます。（再び○と○ですね！！）
6. 再びこの関数は ot_x と ot_y で渡された値を1個ディクショナリ変数のタプル配列に入った数値の指示に従って1つずらして、再び自分の関数を呼びます。
7. 4回目に呼ばれた関数の引数は X=3 , Y=5 になっています。またそこから左隣のコマと、さらにその左隣のコマを調べます。○● と連続するコマが出現したので、黒の位置をひっくり返せる位置として ot_lastposX と ot_lastposY に格納してこの関数は終わります。

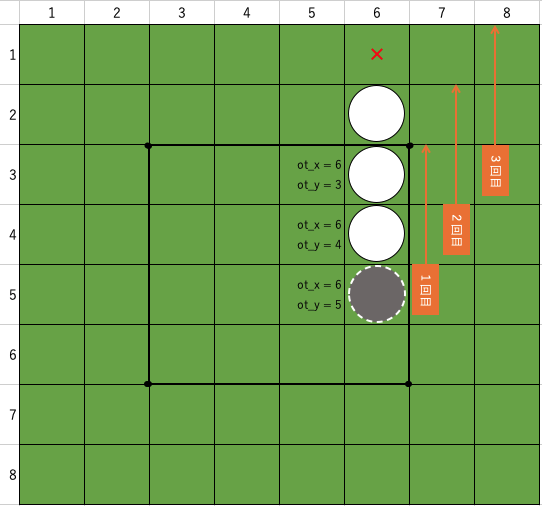
　もしも、左隣のコマと、さらにその左隣のコマが ○○ だった場合でも、1つずらして自分を呼び続けた結果、下図のように○●とならない場合（○・）となるか（○○で終端）は置けないと判断して関数は終了します。

　いかがでしょうか？再帰関数について何となくでも理解できたでしょうか？正直言うと縦横8マスしか無いので、再帰関数にしなくても良いのですが、コードが冗長になりそうなのに加えて、この考え方は応用が効くというポイントも加味して、少し難しいかもしれませんが再帰関数を使ってみました。

　余談ですが、この関数ですが指定方向のコマを1つの文字列にして正規表現で ^○+● で検索して置換してしまうという方法もアリかもな〜？と色々考えましたが、プログラム的に楽しくないのでボツにしましたｗ

    # 次なる一手を置く処理（置けない処理も）
    def ot_next_onepeace(self,ot_x,ot_y,ot_dir):
        # 自分の位置から全方位の次の手が逆手で且つ自手の場合
        nx = self.ot_direction[ot_dir][0]
        ny = self.ot_direction[ot_dir][1]

        # そもそも次の一手は置けない判定
        if ( nx < 0 and ot_x == 1 ) or ( ny < 0 and ot_y == 1 ) or ( nx == 1 and ot_x == 8 ) or ( ny == 1 and ot_y == 8 ):
            return -1

        # 隣の1個をゲットする（自分の手から見て左と上はマイナス方向になる）
        nextpeace = self.ot_peace(ot_x+nx,ot_y+ny)

        # 隣の手が・か自手だったら置けないと判定
        if nextpeace == '・' or nextpeace == self.ot_offdef:
            return -1

        # 隣の隣があるか判定
        cx = ot_x+(nx*2)
        cy = ot_y+(ny*2)

        # 隣の隣がなければ置けないと判定（方向が左か上だったら左端、上端を判断）
        if ( nx < 0 and cx == 0 ) or ( nx > 0 and cx == 9 ) or ( ny < 0 and cy == 0 ) or ( ny > 0 and cy == 9 ):
            return -1

        # 次の次がとれるのでそれを探す
        nextnextpeace = self.ot_peace(cx,cy)

        if nextnextpeace == '・' :
            return -1         # ひっくり返せませんね通知

        if nextnextpeace == self.ot_offdef:
            # ひっくり返せる終端位置を記録する
            self.ot_lastposX = cx
            self.ot_lastposY = cy
            return 1         # ひっくり返せるよ通知

        # 自分の手と自分の手が続いたら、自分の関数をもう一回呼ぶ（再帰）
        return self.ot_next_onepeace(ot_x+nx, ot_y+ny, ot_dir)

指定方向に相手のコマを1つだけひっくり返す関数（これも再帰関数）

　はい、この関数は先ほどの関数とやっていることはほぼ同じです。

　3番目で指定された方向に対して、相手のコマを自分のコマに置き換えていく処理を行っています。但し、この関数も引数で渡されたX座標とY座標の隣のコマしか置き換えを行いません。

　今度は1個ひっくり返したら、ot_x と ot_y で渡された値を1個ディクショナリ変数のタプル配列に入った数値の指示に従って1つずらして、再び自分の関数を呼びます。隣の隣の座標が ot_lastposX と ot_lastposY と合致したら処理を終了します。

    # 手をひっくり返す処理
    def ot_changepeace(self,ot_x,ot_y,ot_dir):
        # 自分の位置から全方位の次の手が逆手で且つ自手の場合
        nx = self.ot_direction[ot_dir][0]
        ny = self.ot_direction[ot_dir][1]
        # 隣の1個をひっくり返す
        nextpeace = self.ot_peace(ot_x+nx,ot_y+ny,self.ot_offdef)

        # 隣の隣が最終位置か判定する
        cx = ot_x+(nx*2)
        cy = ot_y+(ny*2)

        # 隣の隣が最終位置なら終了
        if cx == self.ot_lastposX and cy == self.ot_lastposY:
            return
        return self.ot_changepeace(ot_x+nx, ot_y+ny, ot_dir)

最後のクラス関数2つ解説して終わりです

　ot_peace() 関数ですがこの関数の役割は2つあります。

1. 指定された座標のコマを関数の戻り値として返す
2. 3番目の引数にコマを指定した場合は、指定された座標のコマを引数のコマで置き換えを行います

　Python で面白いなと思ったのは、関数の引数にデフォルト値を指定して、その引数を省略できることです。ですので、ot_peace()を呼び出す時には、引数が2個の場合と、3個の場合があり、それぞれ上記の役割で処理が変わるのです。

　さて、最後のオセロクラスの関数は盤面を表示する関数 ot_display() です。最初にお話ししたと思いますが、この関数は ot_bit 配列に格納されたデータを 8Ｘ8 のマス目に表示することと、●と○の数を表示するという役割を担っています。

   # 指定位置の手を取得する（ついでに書き換えもする）
    def ot_peace(self,ot_x,ot_y,ot_chr=None):
        if ot_chr != None:
            self.ot_bit[(ot_y - 1) * 8 + (ot_x - 1)] = ot_chr
        return self.ot_bit[(ot_y-1)*8+(ot_x-1)]

    # オセロの盤面を表示する
    def ot_display(self):
        print("Ｘ① ② ③ ④ ⑤ ⑥ ⑦ ⑧")
        for l in range(1,9):
            print("{}".format(l), end='' )
            for c in range(1,9):
                print(" {}".format(self.ot_bit[(l-1)*8+(c-1)]), end='')
            print()
        print("            ○：{}　●：{}".format(self.ot_bit.count('○'),self.ot_bit.count('●')))

　以上、いかがでしたでしょうか？難解そうに見えるオセロクラスのプログラムが、徐々に意味のある文章のように見えてきたのではないでしょうか？このプログラムの良さはとりあえず動くということに尽きます。そして、プログラミング上達のステップは他人のソースコードを読むこと、そしてそれを改変していって自分なりに要素を追加して遊んでみることです。

　今回のプログラム解説はこれで終わりですが、また暫くしたら PyQt5 を使ったグラフィカルなオセロゲームを作って、またここに戻ってきます。それまで皆さんも Python で色々いじくり倒して楽しんでくださいね！！

　それではまた！！

c u

    print("to be continue...")