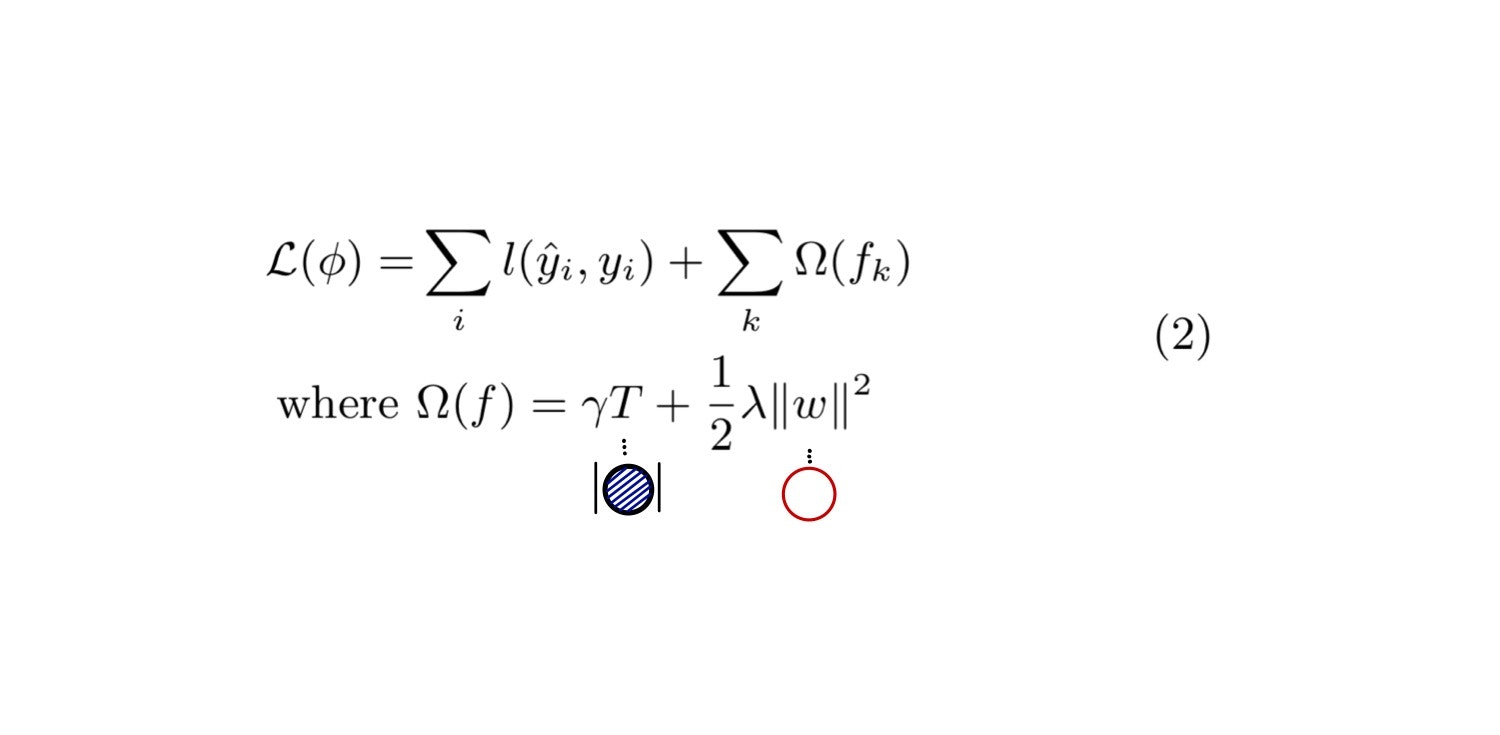はじめに
勾配ブーストを用いた決定木(GBDT)によるクラス分類や回帰はデータ分析コンペでも非常によく使われています。
その中でも2016年に出されたXGBoostはLightGBMと並びよく使われている手法です。
性能が良いことで有名なXGBoost, LightGBMですが、モデル内部でどのような処理が行われているかよくわかっていなかったので論文を読んでみました。
式変形の省略が多く、またイメージしづらい箇所もあり、読みづらかったのですが
一度イメージできれば割とあっさり理解できます。
その体験を踏まえて、イメージ図を多く取り入れながらXGBoostの論文を(途中まで)丁寧に解説します。
XGBoost: A Scalable Tree Boosting System
[論文] (https://arxiv.org/abs/1603.02754)

この記事で述べること
- データの入出力
- XGBoostの木構造
- 損失関数とboosting
- 木構造の学習(split手法)
この記事で述べてないこと
- 実装のフロー
- パラメータチューニングのTips
- メモリ削減のための近似手法
- 大規模データのためのスケール手法(ここが肝)
文量が多くなったので、第1回とします。
(結構疲れました、もしいいねがたくさんもらえたら次回以降も書こうかと。。。)
(追記)
第2回書きました。
XGBoost論文を丁寧に解説する(2): ShrinkageとSubsampling
参考記事
[XGBoost: A Scalable Tree Boosting System] (https://arxiv.org/abs/1603.02754):原著
XGBoost 公式ドキュメント: 論文よりも平易に解説されています。
[XGBoostのお気持ちを一部理解する] (https://qiita.com/kenmatsu4/items/226f926d87de86c28089): みんな大好き@kenmatsu4 さんの記事。この記事を理解されていたら本記事は不要です。
XGBoost論文の解説
XGBoostの構造
データの入出力
入力データ: $\mathcal X$
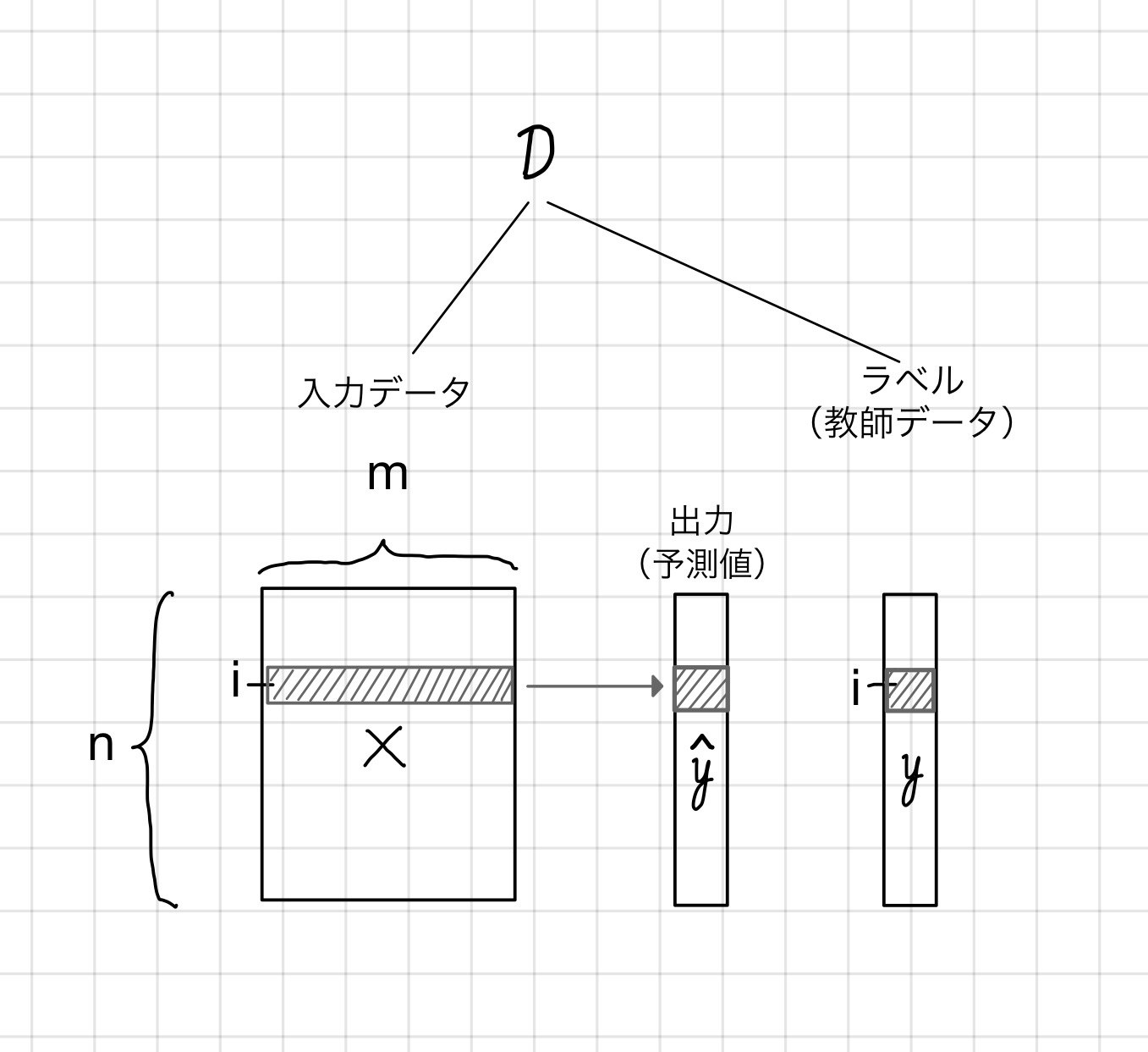
縦(下)方向にサンプル、横(右)方向にデータの属性(特徴量)が並ぶテーブル型のデータ構造を考えます。
サンプル数はn、データの次元数はmとします。また、特定のサンプルを表すインデックスをiとします。
このとき、
i番目のサンプル、XGBoostによる出力値(予測値)、ラベル(教師データ)をそれぞれ
$x_{i}, \hat{y_i}, y_{i}$と表記します。
XGBoostの木構造
決定木の構造

論文のFig.1(抜粋)を使って説明します。
5人の家族がコンピュータゲームを好きかどうかを予測する場合を考えます。(それぞれのコンピュータゲーム好き度を定量化すると言い換えましょう)
家族に与えられた情報(年齢、性別、PCの使用頻度など)を用いて振り分けのルールを作りサンプルを振り分けていくのが木ベースの考え方です。例えば上図のtree1では、
- 年齢が15歳未満か?
- 性別が男か?
といったルールでサンプルを振り分けていきます。ルールにしたがって最終的にたどり着いた木の末端を葉ノード(leaf node)と呼びます。振り分けられた葉ノードに基づいてサンプルを分類するのが決定木によるクラス分類の基本的な考え方です。
木の並列化(アンサンブル)
単一の木を使う場合、データに含まれるノイズに影響を受ける場合があります。そこで、決定木を複数用意して並列化し(アンサンブル)、出力結果をロバストにすることを考えます。
人間でも、一人の人間の決断に従うとときに過激な行動に出ることがありますね。それを避けるために多数決を取るイメージです。
並列化を取り入れた決定木として有名なのはランダムフォレスト(Random Forest)でしょう。サンプルをランダムに繰り返し抽出して、ノイズに強い決定木(群)を作り出します。
上の図では、tree1のほかにtree2を用意しています。出力結果を平均化することにより、最終的な予測を得ます。それぞれの重みを等しくすれば単なる多数決になりますが、一票に重みを付けることを考えます。
XGBoostの構造
さて、ここからXGBoostの構造とデータの入出力について定式化していきます。
XGBoostも並列化された複数の決定木を用います。それぞれの結果をアンサンブルすることで予測値を出力します。下図を基に説明します。
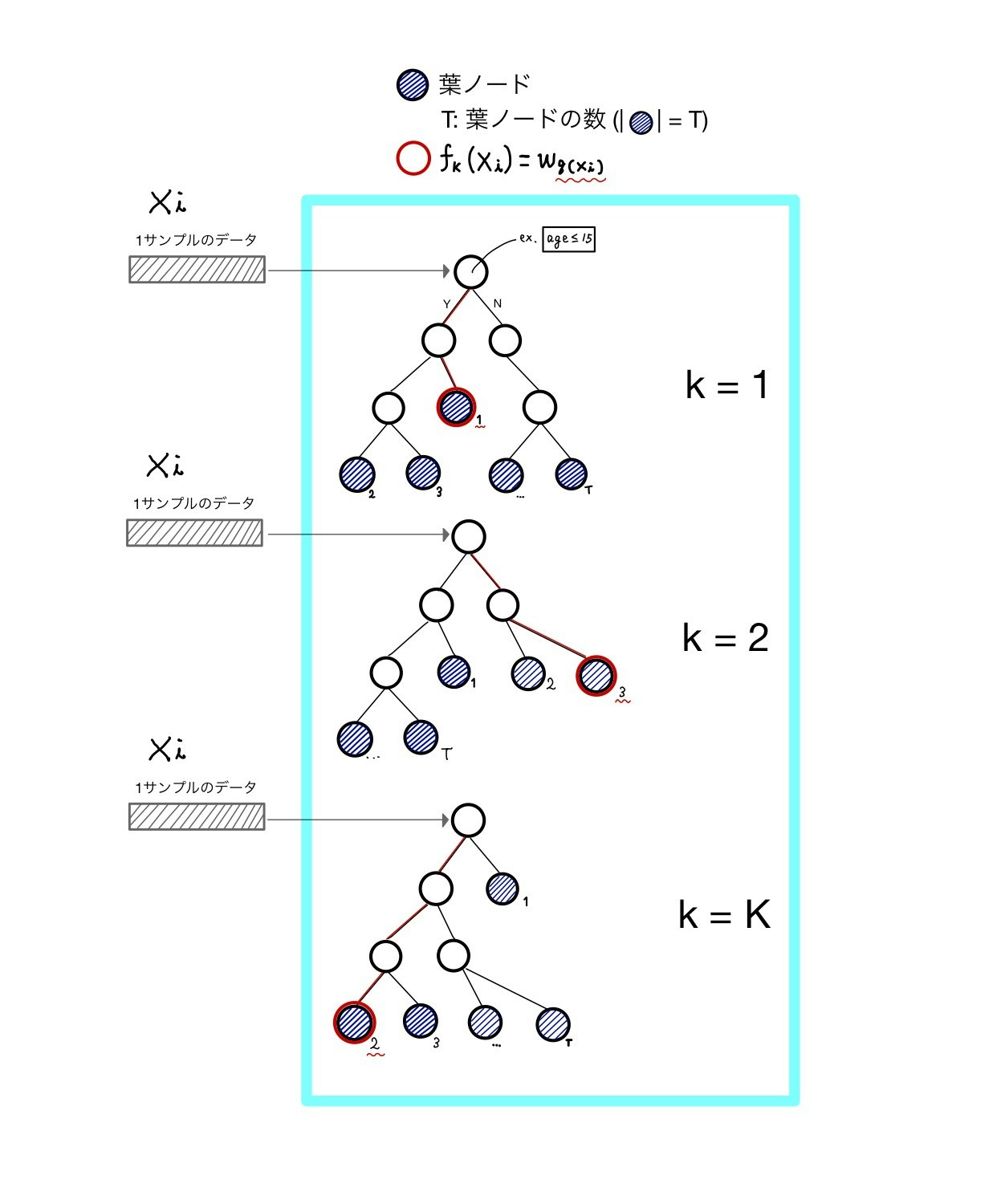
並列化された木の数をKとします。入力データ中の1サンプルデータ($x_{i}$)はそれぞれの木の振り分けルールに従い、最終的な葉ノードに落ち着きます。
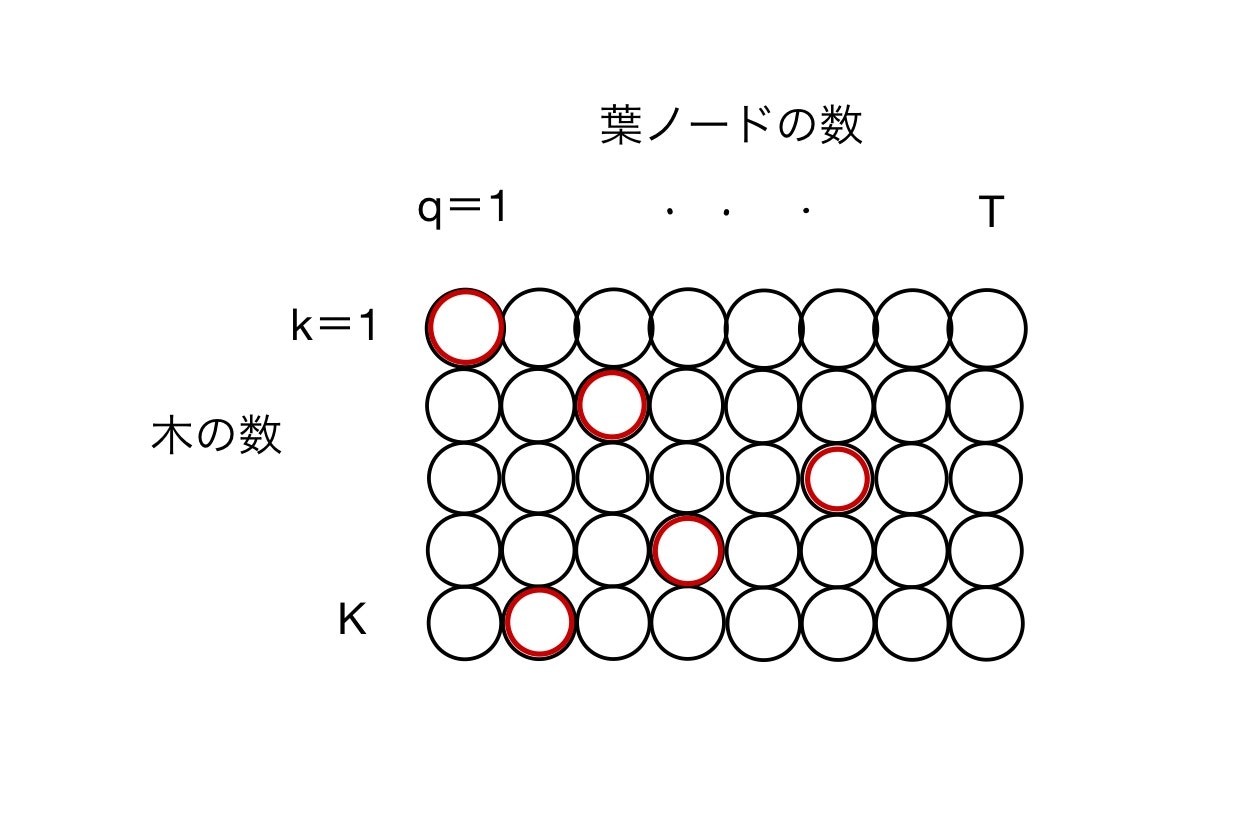
それぞれの木にあるT個の葉ノードをまとめてみましょう。
行番号kが木の数、列番号qがそれぞれの木の葉ノードの数を表しています。
このノードに格納されている値$w$がXGBoostの重み、そして学習する値になります。
注
この図では全ての木について同じ葉ノードの数Tを持っていますが、実際にはそれぞれの木が同じノード数を持つとは限りません。ここでのTは葉ノードの最大数とお考えください。
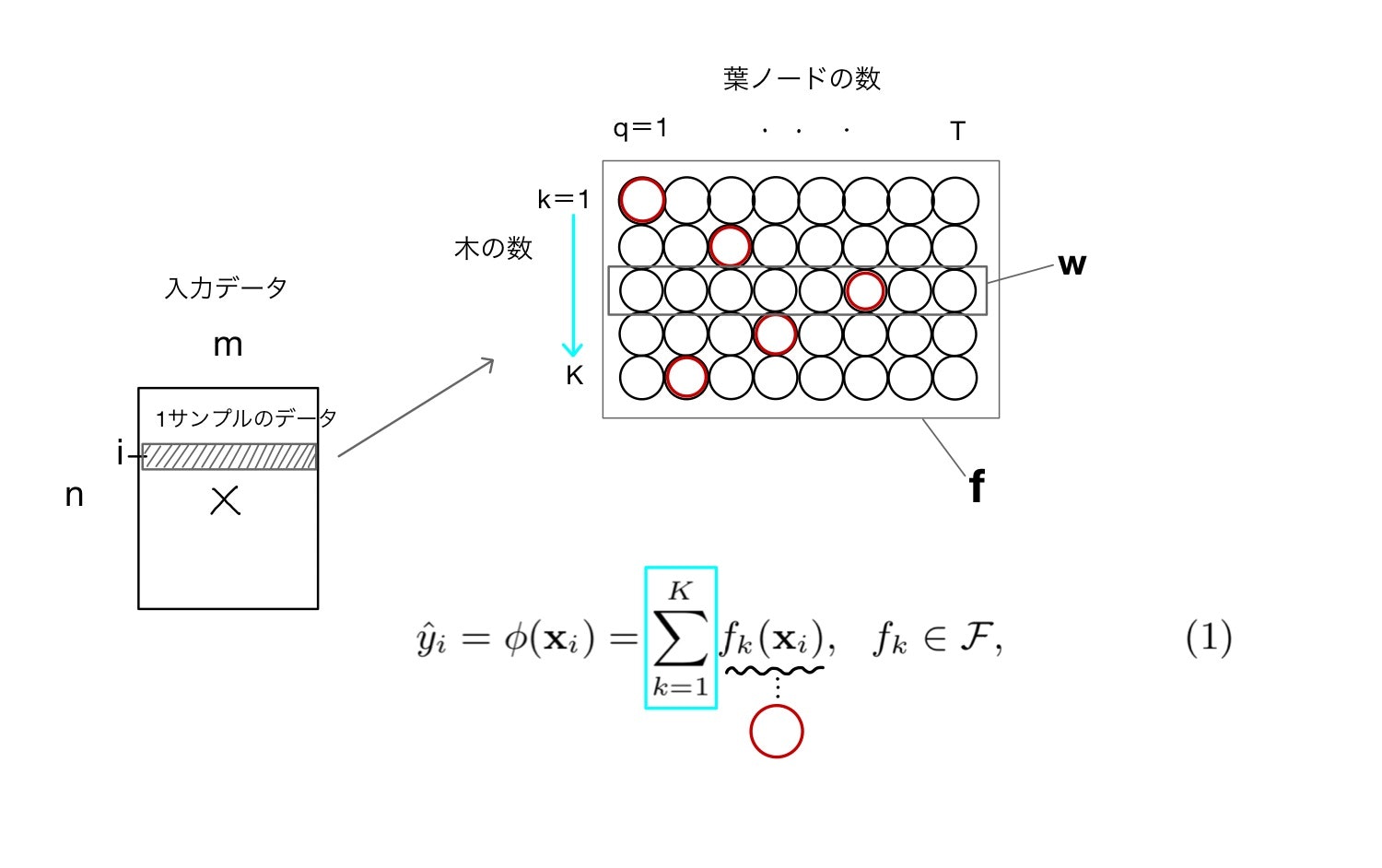
ここまでに様々な記号が出てきましたが、それぞれがどのような入出力関係になっているか整理してみましょう。
- 1サンプルの入力データ$x_{i}$を XGBoostのモデルに与える
- それぞれの木(k)に対して対応する葉ノードの番号qが決まる
- kおよびqから対応する重みが決まる
3の重みを各kに対する1次元ベクトルとして表記しているのが論文中のw、kを含めた2次元ベクトルとして表しているのがfになります。いずれにせよ
$$x_{i} \rightarrow q \rightarrow w_{q} \quad (or : f_{k}) $$
のデータフローをイメージしておいてください。
これでそれぞれの木に対する重みが決定します。最終的な出力($\hat{y}_{i}$)はそれぞれの木の対応する重みを総和したものになります(式(1))
$$\hat{y_i} = \sum_{k=1}^{K} f_k(x_i) \quad \cdots (1)$$
補足:正確には重み×learning rateになります。learning rateに関するテクニックは、その2で解説する予定です。
正則化項付きの損失関数
損失関数を式(2)に示します。
損失関数($\mathcal l$)には、残差二乗平均のような微分可能な凸関数を用います。
各サンプルに対して予測値と教師データとの間の残差を$\mathcal l$で表現し、全てのサンプルに対して総和します。
さらに、第2項目にXGBoostに特有の正則化項があり、それぞれの木に対する$\Omega$の寄与を総和します。
正則化項$\Omega$はさらに$T$と$||\omega||^{2}$に分解できます。
$T$(葉ノードの数)が大きくなるほど損失関数が大きくなるため、木の構造を複雑化するのを抑える効果があります。
$||w||^2$は重み$w$のL2ノルムであり、これも過学習を抑える効果があります。
$\gamma$および$\lambda$はそれぞれの正則化項のバランスを調整するパラメータです。
Gradient Tree Boosting
ここからはXGBoostの学習について見ていきます。
XGBoostのモデルを決定するには
- 木の構造を決定する
- 各葉ノードの出力($f_k(x_i)$もしくは$w_q$)を決定する
必要があります。2から見ていきましょう。
損失関数(式(2))を最小化するような重み$f_k(x_i)$もしくは$w_q$を求めたいのですが、これらの変数はサンプルに依存する値(つまり関数)であるので、通常の最適化手法(例えば確率的勾配降下法)を使うことができません。
そこで、勾配ブースティングでは論文中で”Additive manner”と呼ばれる方法で学習を行い、$f_k(x_i)$を更新して損失関数を下げていきます。下図で説明します。
勾配ブースティングにおける漸化式
注
(2018.08.09)
勾配ブースティングではK=1(単一の木構造)から始まり、ラウンド毎に木の数を増やしていくとのコメントをいただきました(2019.08.09)。この図では初めからK個の木構造があることになっています。確認して図と文を修正予定です。
(2018.08.10)
図と文を修正しました(以下)
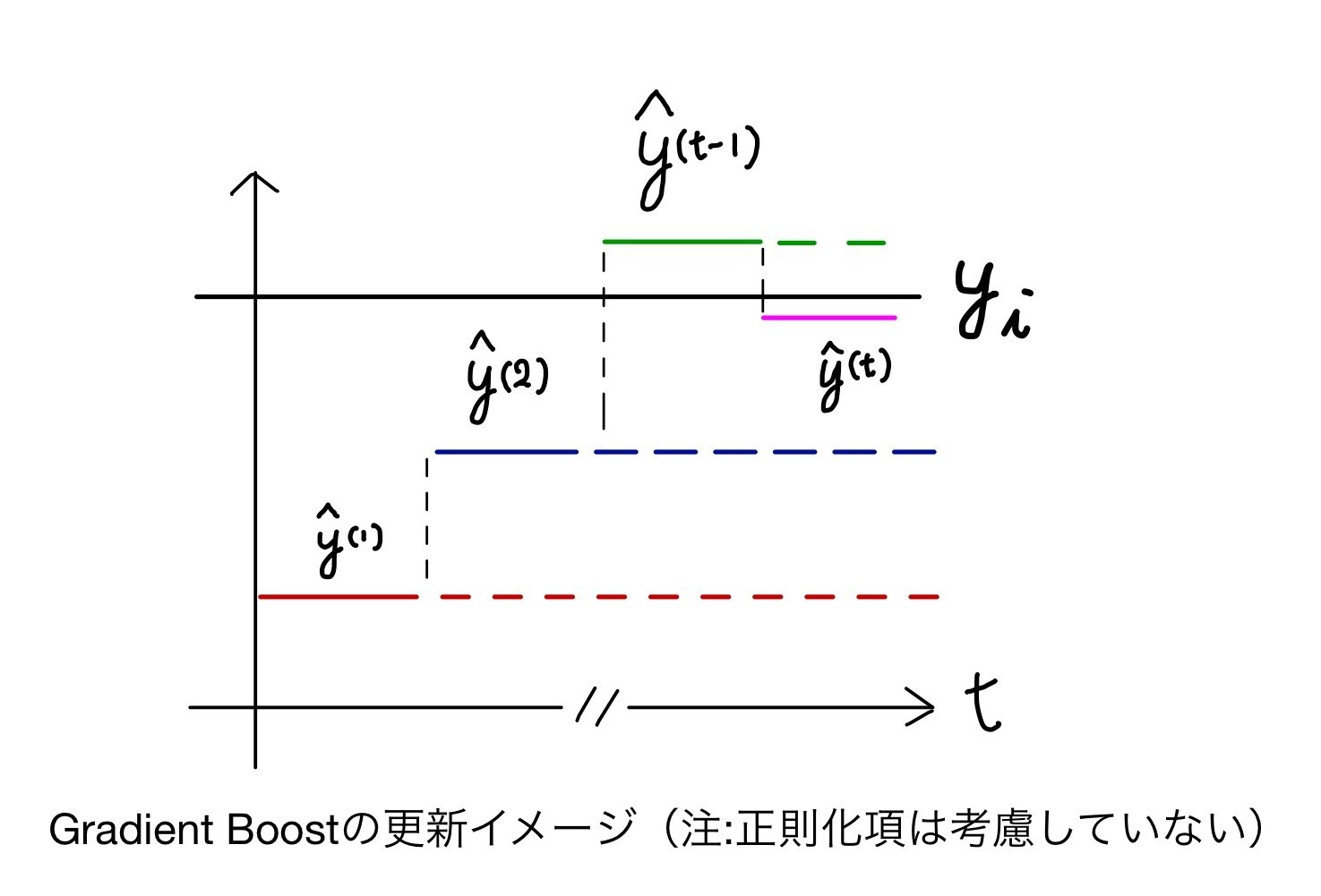
初期状態($t=1$)では、単一の決定木のみが存在します(赤枠)。
1ステップ進めt=2の時に、新しい木を追加することを考えます。
最終的な出力は一つ前の出力に新しく追加された木を加えます。
つまり、以下の式が成り立ちます。
$$\hat{y_i^{(t)}} = \hat{y_i^{(t-1)}} + f_t(x_i)$$
この時、新しい木は真の値とのギャップを埋めるものを採用します。
以下のイメージ図を見たほうが早いでしょう。
このようにして、反復を繰り返しながらモデルの出力値を真の値に近づけていきます。
損失関数(勾配ブースティング版)
XGBoostの出力値を真の値に近づけるために$\hat{y_{i}}^{(t)}$を$t$に関する漸化式の形で表しました。
この漸化式を用いて損失関数を書き直すと
\begin{align}
\mathcal L^{(t)} &= \sum_i^{n} \mathcal l\,(y_i^{(t)}, \hat{y_i}^{(t)}) + \Omega (f_k) \\
&= \sum_i^{n} \mathcal l\,(y_i^{(t)}, \hat{y_i}^{(t-1)} + f_t(x_i)) + \Omega (f_k) \quad \cdots (*)
\end{align}
となります。
注
前出の損失関数$\mathcal L$に対して、漸化式版の損失関数$\mathcal L^{(t)}$では$\Omega$に対する総和$\sum_k$の記述がなくなっています。
論文中これに対する言及は特にないので推測に過ぎませんが、漸化式版の損失関数ではそれぞれの木に対する損失関数を見ていると考えられます(間違っていたら教えてください)
とにかく、今後の議論では決定木の数$k$に対する総和$\sum_k$は考えずに議論が進みます。
(2019.08.09) コメントいただきました。ありがとうございます。
(中略)Boostingでは各ラウンドtごとに木をどんどん増やしていきます. そのため, 現在のラウンドtに付随する変数のみが学習すべき対象となります.
したがって$\mathcal L^{(t)}$で学習すべき変数, 最適化したい変数は$f_t$, $w_t$(tラウンド目での木の情報)であって,
tラウンドにおいてはw_1...w_(t-1)は定数扱いとなります. なので正則化項の∑kのうちtのみ考えれば良い, という流れだと思います.
勾配ブースティングの最適解
テイラー展開
こうして得られた損失関数(*)を見ると、関数 $l(•,•) $の中に最適化したい変数(関数)$f$が入っています。
この$f$を$l$の外にくくり出すことを考えます。
関数$F$の$x$の周りのテイラー展開を2次の項まで近似すると
$$F(x + \Delta t) \simeq F(x) + \frac{dF}{dx} (\Delta x) + \frac{1}{2!} \frac{d^2F}{dx^2} (\Delta x)^2$$
になります。$F$を$l$、$x$を$\hat{y_i}^{(t-1)}$、$\Delta x$を$f_t(x_i)$と置き換えると、
\begin{align}
\mathcal L^{(t)} &= \sum_i^{n} l\,(y_i^{(t)}, \hat{y_i}^{(t-1)} + f_t(x_i)) + \Omega (f_k) \\
&= \sum_i^{n} [l\,(y_i^{(t)}, \hat{y_i}^{(t-1)}) + \frac{\partial }{\partial \hat{y_i}^{(t-1)}} \,l\,(y_i^{(t)}, \hat{y_i}^{(t-1)})\, f_t(x_i)
+ \frac{1}{2!} \frac{\partial^2}{(\partial \hat{y_i}^{(t-1)})^2}\,l\,(y_i^{(t)}, \hat{y_i}^{(t-1)})\, (f_t(x_i))^2]
+ \Omega (f_k) \\
&= \sum_i^{n} [l\,(y_i^{(t)}, \hat{y_i}^{(t-1)}) + g_i \, f_t(x_i)
+ \frac{1}{2} h_i \, f^2_t(x_i)]
+ \Omega (f_k) \\
\end{align}
を得ます。ただし
\begin{align}
where \quad g_i &= \frac{\partial }{\partial \hat{y_i}^{(t-1)}} \,l\,(y_i^{(t)}, \hat{y_i}^{(t-1)}) \\
h_i &= \frac{\partial^2}{(\partial \hat{y_i}^{(t-1)})^2}(l\,(y_i^{(t)}, \hat{y_i}^{(t-1)}) \\
f_t^2(x_i) &= (f_t(x_i))^2
\end{align}
です。
ここで、$l,(y_i^{(t)}, \hat{y_i}^{(t-1)})$は $f_t(x_i)$に依存しない関数なので$\mathcal L^{(t)}$の中で定数項としてみなせます。
この定数項を無視した損失関数を再定義することで
$$ \tilde{\mathcal {L}}^{(t)} = \sum_i^{n} [g_i , f_t(x_i)
+ \frac{1}{2} h_i , f^2_t(x_i)]
- \Omega (f_k) \quad \cdots (3) $$
を最終的に得ます。
総和の変換トリック
さて、数式が出てきました。頭がゴチャゴチャしてきましたね。ラップアップしましょう。
- XGBoostの出力および損失関数をステップ数$t$に関する漸化式で書き直す
- テイラー展開により最適化したい変数$f$を損失関数(の中の関数$l$)からくくり出す
- 定数項を無視したシンプルな損失関数を新たに得る
こんなに式をこねくり回す目的は何だったかというと、最適化したい変数$f$のためです。
端的に言えば変数$f$の最適解を得ることです。
それを念頭においてもう少し進みましょう。
式(3)の正則化項$\Omega$を定義通りに書き換えます。
$$ \tilde{\mathcal {L}}^{(t)} = \sum_i^{n} [g_i , f_t(x_i)
+ \frac{1}{2} h_i , f^2_t(x_i)]
- \gamma T + \frac{1}{2} \lambda \sum_{j=1}^{T}w_j^2 $$
右辺第1項には$\sum_i^{n}$、第3項には$\sum_j^T$の記号がありますね。
この記号の意味を図で示します。
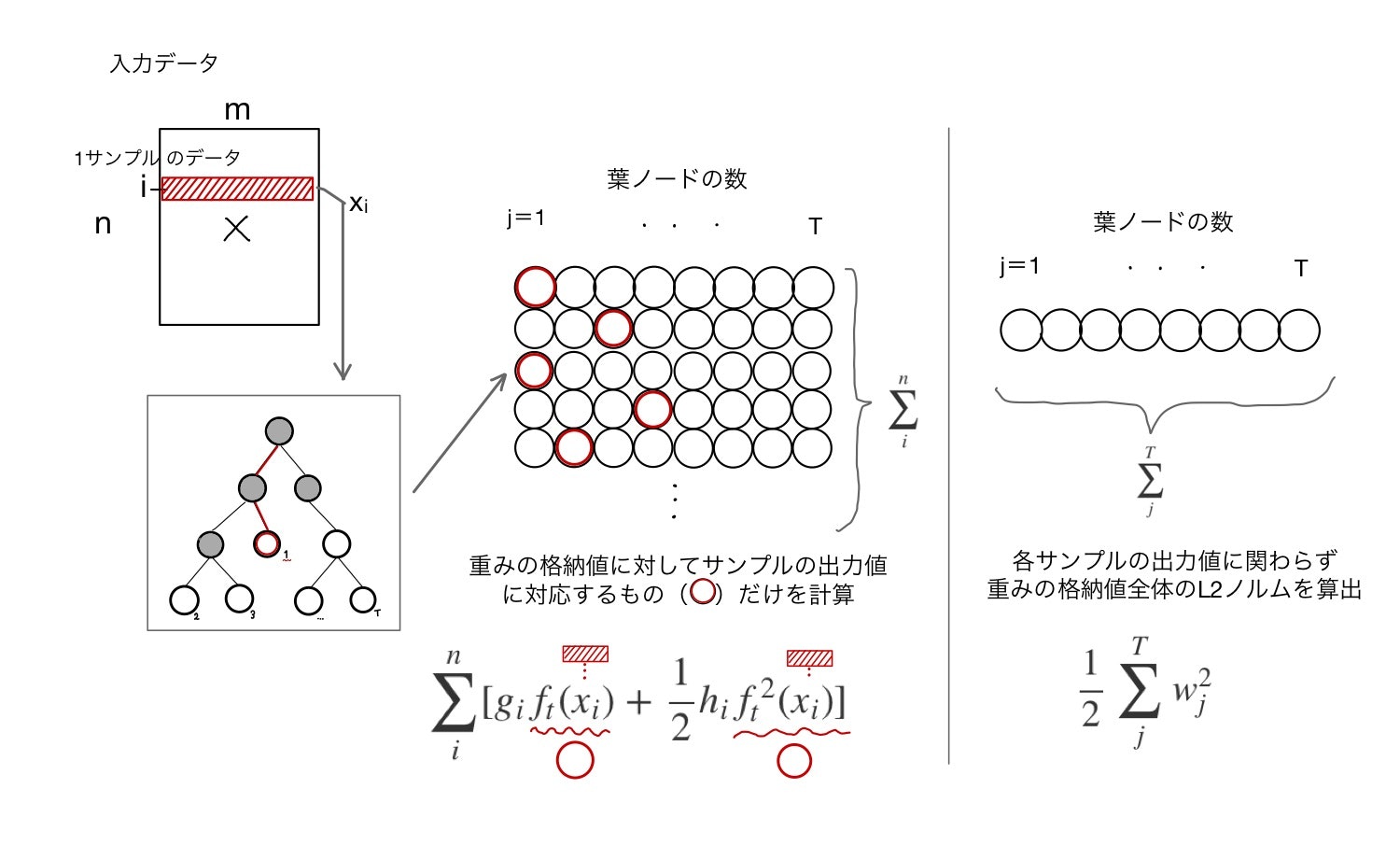
まずは第1項目
1サンプルのデータ$x_i$を単一の決定木に入力したとき、T個ある葉ノードのうちの一つの出力値が対応します(図の赤丸)。
その出力値に対して$g_i$や$h_i$を掛けたり、2乗したりした後に全サンプルの総和を取ったものになります。
つぎに第3項目
この項は正則化項の一部です。サンプルの出力値とは関係なく、対応する木のT個の葉ノードの出力値(重み)の総和の総和を取ります。
注
左の図で表した丸($f_t(x_i)$)と、右の図で示した丸($w_j$)は記号が違うが同じものです。もし忘れていたら上の方の説明を読み返してください。あとで使います。
第1,3項目で総和の方向(変数)が違いますね。これを意識してください。
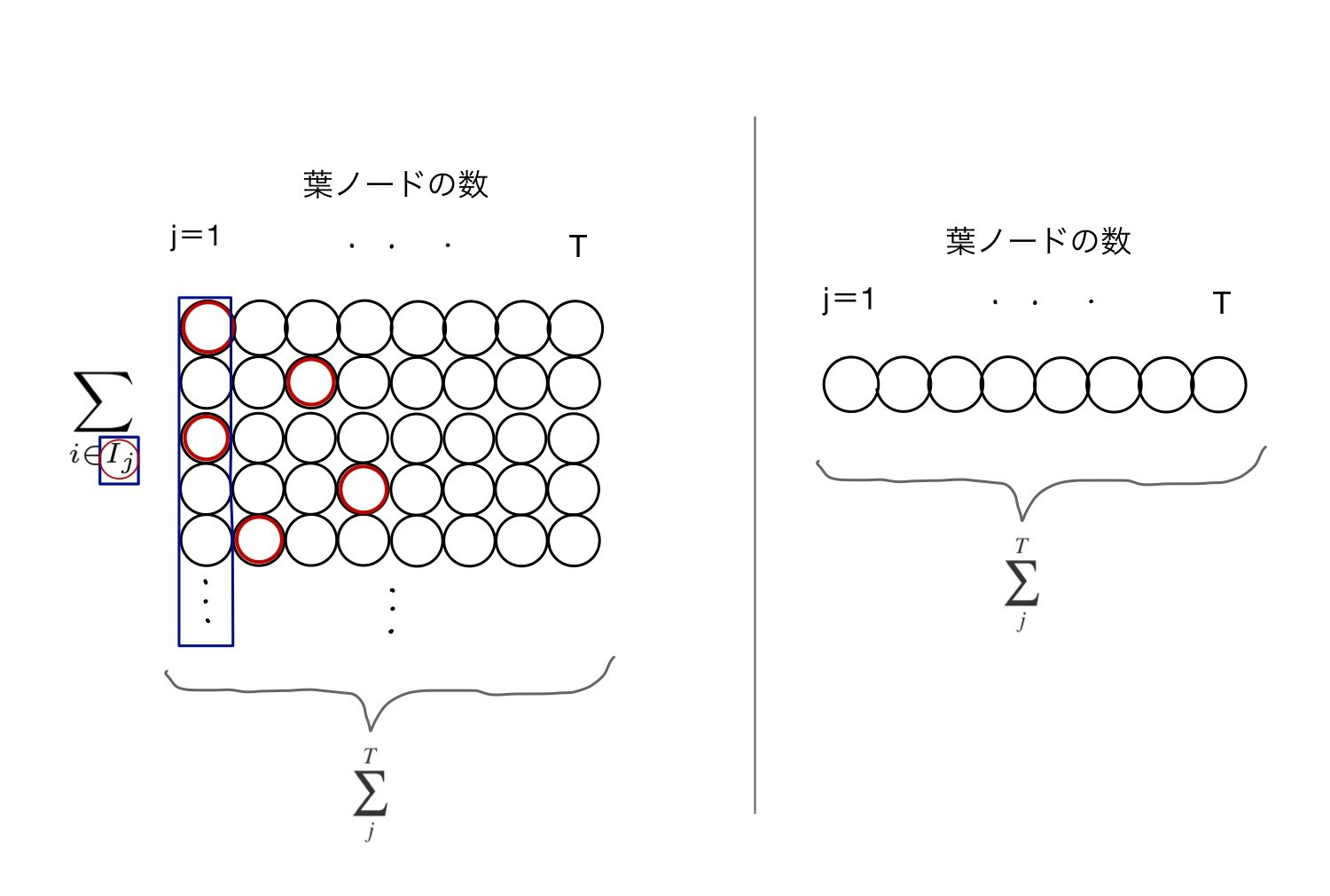
ここで一つトリックを使います。総和の方向を揃えます。
右辺第1項(上図の左)に関して、サンプル方向(下方向)に足していった総和$\sum_{i}$をやめて、第3項(上図右)のように横方向(ノード方向)$\sum_j^T$の総和に変えます。
図で囲まれた青枠の値を横方向に総和していくイメージです。
ただし、青い長方形の中の実際に出力されたノード(赤丸)のみを足す必要があります。
これを表現するために、j列目の全サンプル集合から実際に出力されたサンプルの部分集合(つまり青長方形中の赤丸全体)を$Ij$と表します。
そしてこの赤丸だけの総和をとることを$\sum_{i \in I_j}$と表します。
この形式で損失関数を書き直してみましょう。
$$ \tilde{\mathcal {L}}^{(t)} = \sum_{j=1}^T \sum_{i \in I_j} [g_i , f_t(x_i)
+ \frac{1}{2} h_i , f^2_t(x_i)]
- \gamma T + \frac{1}{2} \lambda \sum_{j=1}^{T}w_j^2 $$
出力値$f_t(x_i)$を$w_j$で書き換え、式を変形します。
$$ \tilde{\mathcal {L}}^{(t)} = \sum_{j=1}^T [(\sum_{i \in I_j} g_i) , w_j
+ \frac{1}{2} (\sum_{i \in I_j} h_i) , w_j^2]
- \gamma T + \frac{1}{2} \lambda \sum_{j=1}^{T}w_j^2 $$
$\sum$の方向を揃えたことで、最適化したい変数$w_j$について括ることができます。
$$ \tilde{\mathcal {L}}^{(t)} = \sum_{j=1}^T [( \sum_{i \in I_j} g_i) , w_j
+ \frac{1}{2} ( \sum_{i \in I_j} h_i + \lambda) w_j^2]
- \gamma T \quad \cdots (4)$$
最適解の導出
式(4)を使って、固定された決定木(つまり$x_i$に対して対応する葉ノードが変化しない)場合の、j番目の葉ノードの最適解を求めます。
損失関数(微分可能な凸関数)の最小値$w_j^*$を求めるために、損失関数を微分してゼロとおきます。
\begin{align}
\frac{\partial \tilde{\mathcal L}^{(t)}}{\partial w_j} &= \frac{\partial}{\partial w_j}(
\sum_{j=1}^T [( \sum_{i \in I_j} g_i) \, w_j
+ \frac{1}{2} ( \sum_{i \in I_j} h_i + \lambda) w_j^2]
+ \gamma T) \\
&= (\sum_{i \in I_j}g_i) + (\sum_{i \in I_j} h_i + \lambda) w_j \\
&= 0 \\
\end{align}
よって$w_j$の最適解
$$ w_j^* = - \frac{\sum_{i \in I_j} g_i}{\sum_{i \in I_j} h_i + \lambda} \quad \cdots (5)$$
を得ます。ようやくたどり着きました。
ここまでを一言でまとめましょう。
固定された木構造におけるXGBoostの最適解の近似値は解析的に求まり、その値は式(5)である。
最適解における損失関数
最適解における損失関数の値を得るために式(4)に$w_j^*$を代入します。
\begin{align}
\tilde{\mathcal {L}}^{(t)} &= \sum_{j=1}^T \left[\left( \sum_{i \in I_j} g_i\right) \, \left(- \frac{\sum_{i \in I_j} g_i}{\sum_{i \in I_j} h_i + \lambda}\right)
+ \frac{1}{2} \left( \sum_{i \in I_j} h_i + \lambda\right) \left(- \frac{\sum_{i \in I_j} g_i}{\sum_{i \in I_j} h_i + \lambda} \right)^2\right]
+ \gamma T \\
&= - \frac{1}{2} \sum_{j=1}^{T} \frac{(\sum_{i \in I_j}g_i)^2}{\sum_{i \in I_j}(h_i + \lambda)} + \gamma T \quad \cdots (6)\\
\end{align}
式(6)により、固定された構造における損失関数の最小値が求まりました。この値は一種の基準となります。
つまり、構造を変えた後のスコアが構造を変える前のスコアより良ければ(低ければ)変えた後の構造の方が良い構造である、と言えます。
決定木の構造を変えるアプローチが見えてきましたね。
木構造の学習
ノードの分割
前章までで、ノードに対する損失関数の最小値が求まりました。これにより、木の構造を変化させた前後の損失関数の値の差を見ることで構造変化を採用するかを決めることができます。
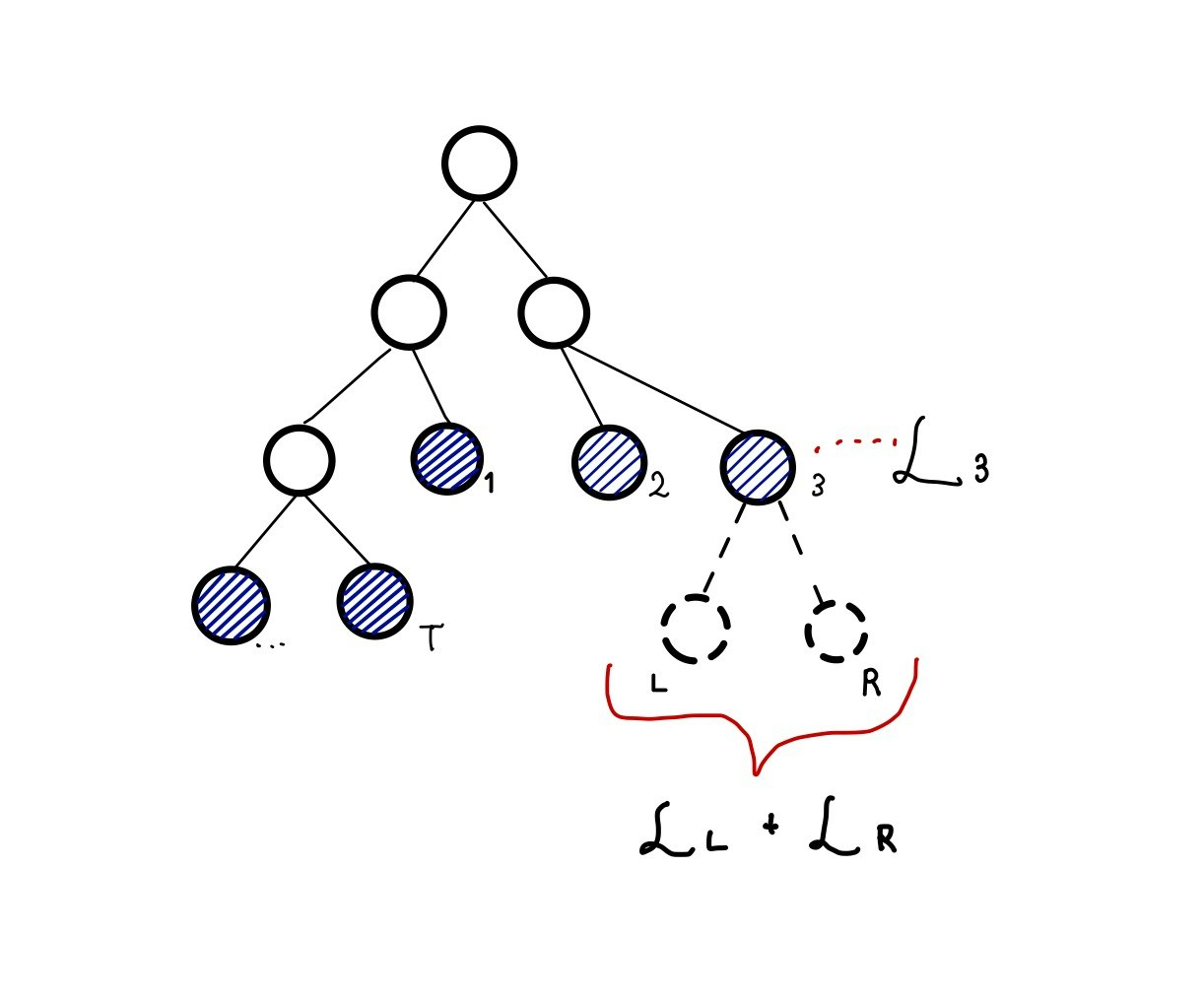
上図のような木構造があるとして、3番目の葉ノードをさらに分割するべきかどうかを考えます。
分割しなかった時の損失関数を$\mathcal L$、分割した後のノードをそれぞれ、$\mathcal L_L$, $\mathcal L_R$として、分割前後の損失関数の差を$\mathcal L_{split}$で定義します。符号に注意して
\begin{align}
\mathcal L_{split} &= \mathcal L - (\mathcal L_L + \mathcal L_R) \\
&= \frac{1}{2}[\frac{(\sum_{i \in I_L} g_i)^2}{\sum_{i \in I_L}h_i + \lambda}
+ \frac{(\sum_{i \in I_R} g_i)^2}{\sum_{i \in I_R}h_i + \lambda}
- \frac{(\sum_{i \in I} g_i)^2}{\sum_{i \in I}h_i + \lambda}] - \gamma \quad \cdots (7)\\
\end{align}
を得ます。
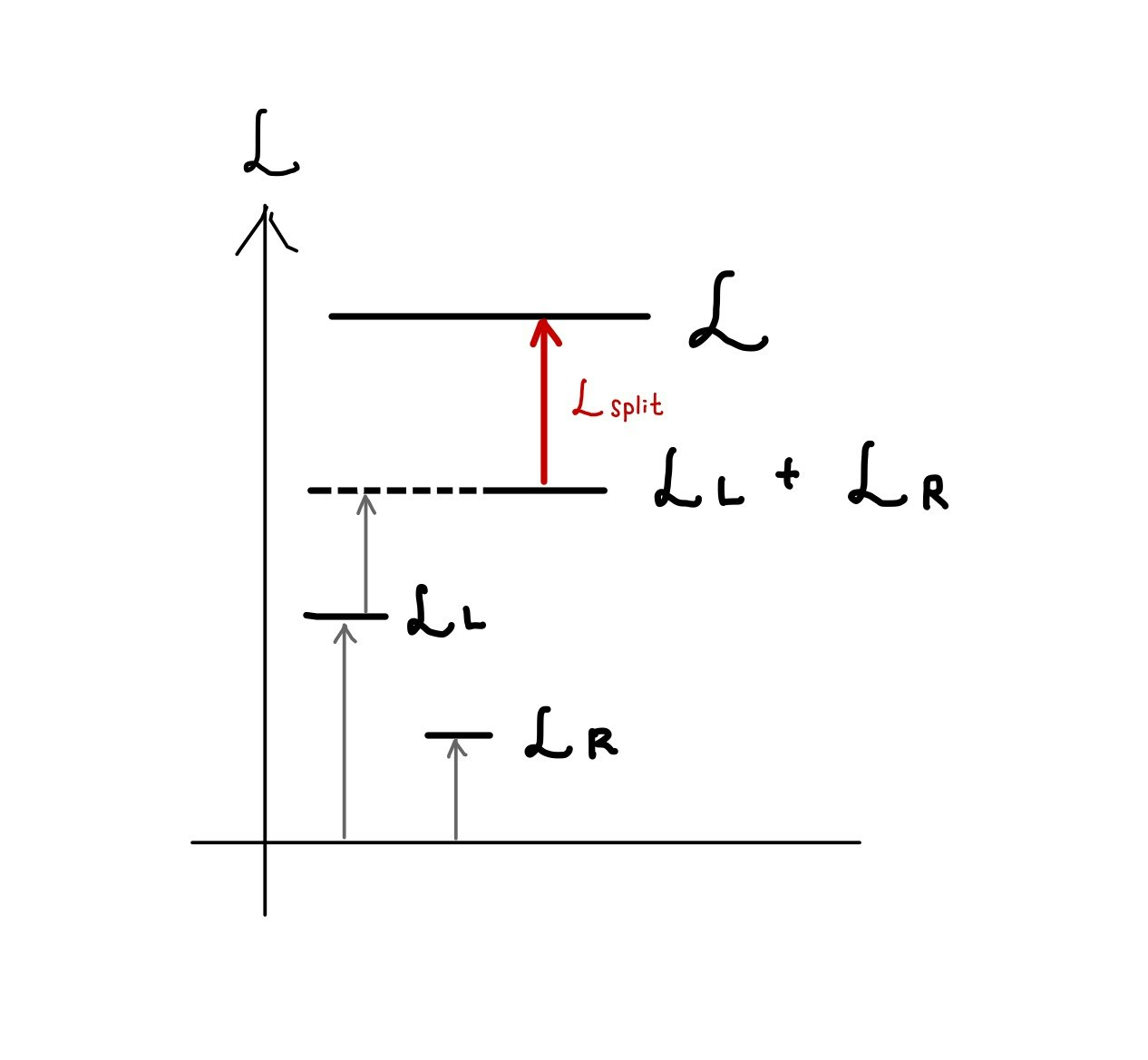
$\mathcal L$, $\mathcal L_L$, $\mathcal L_R$, $\mathcal L_{split}$の関係をエネルギー準位図で表すと以下のようになります。
$\mathcal L_{split}$は分離後から分離前のエネルギー変化を表してますから、この値が正になる時が分割が有効な時です。
このようにして得られた$\mathcal L_{split}$の値を評価することで、木の構造を変化させることができます。
次回
ここまでで、XGBoostの基本的な考え方をまとめました。
長くなったので、一度ここで切ります。
次回は実装のフローの解説や、大規模データスケールさせるための工夫について解説する予定です。