はじめに
第1回の記事で原著論文に沿ってXGBoostの基本事項を学習しました。(論文の2.2まで)
第2回は論文読みをさらに進めていきます。
特に勾配ブースティング法で用いられる学習率の概念をXGBoostにもそのまま適用します。学習率とラウンド数のトレードオフについて説明し、この二つのパラメータはチューニングすべきではないことを記述しました。
- 勾配ブースティング法とその進化版としてのXGBoost(2章)
- 正則化項$\Omega$(※) 前回
- 過学習防止のためのテクニック [今回]
- 木分割のアルゴリズム(3章)
- オンメモリ処理のための近似手法(※)
- スパースなデータへの対応 (※)
- NaNデータへの対応(※)
- スケールアウトのためのシステムデザイン(4章)
- 並列処理(+α?未読)
- 評価(6章)
(※がXGBoostとしての特徴)
しっかり読むと結構分量が多いですが、できるだけ読み進めていきます。(今回は短めです)
過学習防止のためのテクニック
第1回では、過学習を防ぐために、XGBoostの損失関数に正則化項($\Omega$)を導入しました。
加えて、原著2.3章では過学習を防ぐため以下のテクニックが紹介されています。
- Shrinkage
- Column Subsampling
Shrinkage
第1回でXGBoost(というよりGBGTの出力値)が以下のように書けることを説明しました。
$$\hat{y_i^{(t)}} = \hat{y_i^{(t-1)}} + f_t(x_i)$$
時刻(ラウンド)$t$での出力値は、1時刻前の出力値に新しい木の出力を足したものになります。この時、新しい木は真の値とのギャップを埋めるものを採用します。
ところが、新しい木でギャップを全力で(定性的な言い方ですが…)埋めてしまうと、ブースティング法の性能が良いために簡単に過学習してしまいます。
そこで、新しい木の出力$f_t$に学習率に相当する定数$\eta$ ($0 < \eta < 1$)をかけ、出力値を縮小(shrinkage)します。
$$\hat{y_i^{(t)}} = \hat{y_i^{(t-1)}} + \eta ; f_t(x_i)$$
ターゲットである$y_i$に対して最もギャップを埋めるような木を構築するのですが、実際のブースティングではその木の出力は$\eta$倍されるため、論文の言い方を借りると全力(つまり$\eta = 1$)よりもconservative(保守的)に学習は進みます。
そのため、学習率$\eta$を下げるほど学習の進みが遅くなり、学習にかかる時間は増加します。
つまり、学習率$\eta$と学習に必要なラウンド数tはトレードオフの関係になります。
理屈としては$\eta$を下げるほど精密に関数近似できるため、予測器としての性能は良くなります。しかし、代償として計算時間が増大するため有限の時間では計算が終わらなくなります。
学習率のとラウンド数の設定
XGBoostやlightGBMに関する記事や意見をネット上で見ると、学習率(Learning rate)とラウンド数(n_estimators)をチューニングするなという意見をよく耳にします。
ラウンド数の上限に達した場合、そこで学習が強制的にストップするため、特に低いlearning rate、少ないラウンド数を設定した場合、学習が不十分になります。
「じゃあ、どこまでラウンド数を上げるか?」の疑問のものと、ラウンド数を振ってグリッドサーチしようと考えますが、これはしてはいけません。(パラメータ警察が飛んできます)
理由は
- 長いラウンド数は短いラウンド数を含んでいる
- ブースティングの原理上、5000ラウンドの学習は2000ラウンドの学習を含んでいるので、わざわざ短いラウンド数を試す必要はない
- Early stoppingを用いればよい
- 損失関数に改善が見られなかった時にそこで学習を打ち止めにすればラウンド数の上限を探る必要はない
詳細については以下が参考になりました。
天色グラフィティ: なぜn_estimatorsやepochsをパラメータサーチしてはいけないのか
学習率$\eta$についても、低いほど良いため、計算時間との兼ね合いでパラメータを振らずに固定することが多いようです。
$\eta$の値はどれくらいが良いかを調べました。GBGTの考案者Friedmanの論文では0.1以下にするようにとかいてありました。
さらにGBGTのハイパーパラメータについて説明してあるサイトを引用します。
下図に示すのはサイト内のlearning rateに関する情報です。
Laurae++:xgboost/LightGBM parameters

Behaviorの章に、”通常小さい値が良く典型的には0.5”との記述があります。
また、Beliefsの箇所には、”一度固定したら変えるな"、”ハイパーパラメータだと考えるな”、”オプティマイザに渡すな”など、learning rateを変えるべからず的なことが何度も書いてあります。
やはり、0.1以下の値を用いるのが良いと思われます。XGBoostのデフォルト値は0.3と大きめの値になっているので注意です(非力なPCで回すことも想定した値なのでしょうか)
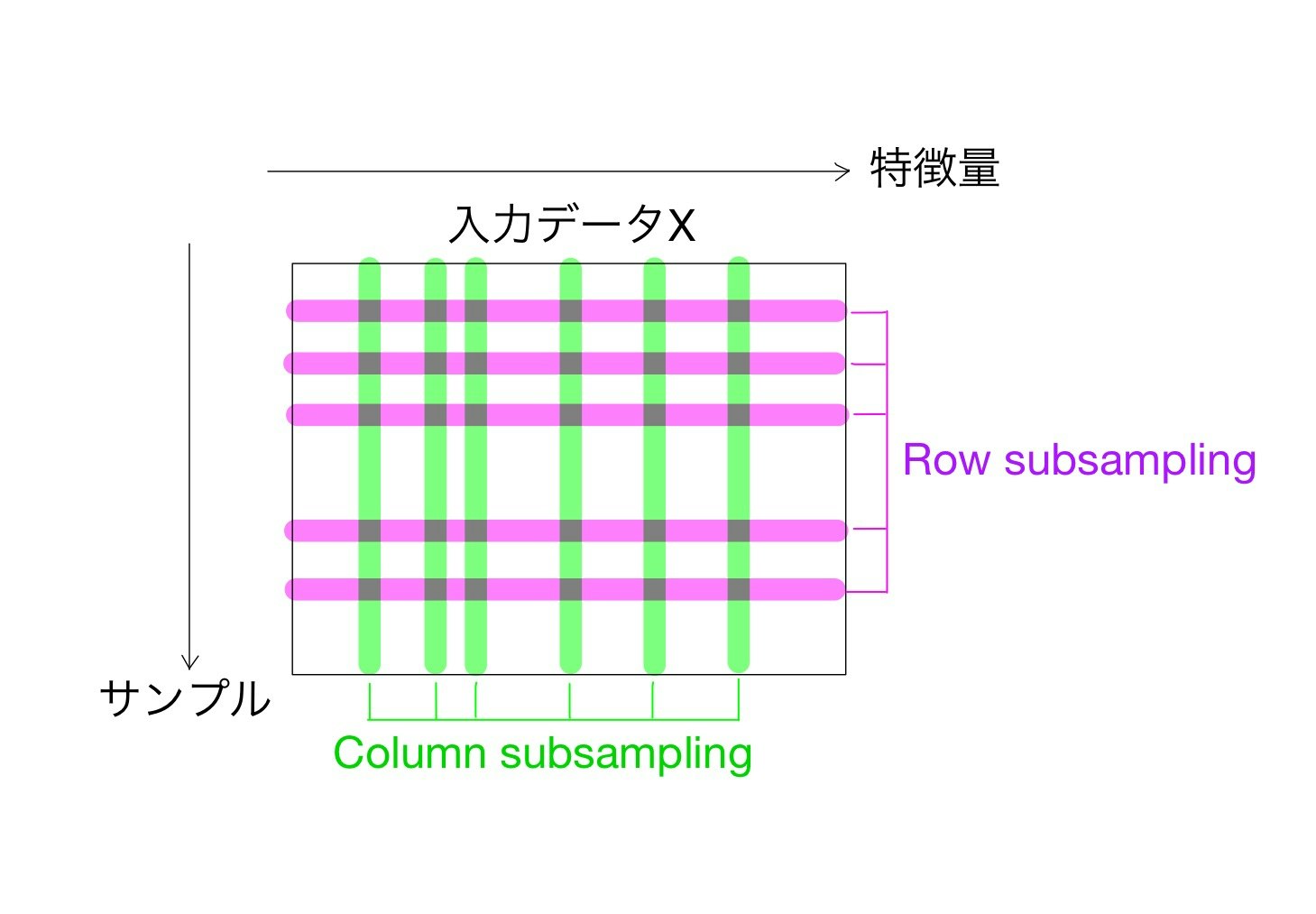
Column subsampling
Shrinkageに続き、もう一つの過学習防止テクニックであるColumn subsampling(おまけにrow subsampling)を解説します。といっても、発想はシンプルです(Random forestにも使われている手法です)
訓練時の各ラウンド毎に入力データの全ての特徴量を用いるのではなくその中のいくつかのものだけを採用します(subsampling)。列方向へのサブサンプリングになることが名前の由来です。
逆に、サンプル方向にサブサンプリングすることをrow subsamplingと言います。
木ごとに列のサブサンプリングを変える手法をColumn subsampling by tree
木のレベルごとに変える手法をColumn subsampling by tree
ノードごとに変える手法をColumn subsampling by node
と言い、別々に調整できるようになっています。
チューニング方法などは上記のサイトを参照してください。
今回のまとめ
Round, learning rateはチューニングしない