はじめに
これまでの記事で、動的計画法(DP法)およびモンテカルロ法(MC法)を用いて強化学習問題を解いて来ました。DP法とMC法の特徴は以下のようになります。
| 手法 | 価値関数の計算 | ブートストラップ | 環境に関する知識 |
|---|---|---|---|
| DP法 | 遷移確率 | 使える | 必要 |
| MC法 | サンプリング | 使えない | 不要 |
DP法ではブートストラップを用いるため、推定しようとしている価値関数を次の状態(行動対)の価値関数を用いて計算することができます。しかし、エピソードを進めるために環境に対する知識、つまり行動$a$をとったときの状態$s'$への遷移確率がわかっている必要があります。
MC法ではサンプリングに基づいてエピソードを生成し、得られた収益を平均することで価値関数の期待値計算をおこないます。この方法では環境に対する知識を必要とせず、得られた報酬およびその総和としての収益をメモリに貯めていけば良いのでした。しかし、エピソードが終了するまで待たなければならないこと、また報酬のみを扱うためブートストラップを使わないことがネックでした。
今回はTD学習(時間的差分学習: Temporal Difference Learning)と呼ばれる手法により、上記のDP法とMC法の利点を掛け合わせた学習をおこないます。すなわち、環境に関する知識を必要とせずにエピソードを前進させつつ、ブートストラップにより逐次(エピソード終端まで待たずに)価値関数を更新します。
期待値(平均)計算の漸進的な考え方
TD法に入る前に、モンテカルロ法で行っている期待値計算を時間の関数として逐次的に処理する考え方を導入します。期末テストの例で説明します。
期末テスト
あるクラスには生徒が10人在籍しています。ある日生徒たちは5教科の期末テストを受け、結果は以下でした。
185, 348, 419, 407, 250, 323, 364, 355, 389, 359
この時の平均点を求めます。平均点$a_{k}$は各点数($r_i$)の合計をデータ点の数で割れば良いので
3399/10 = 339.9点になります。
これを式で表すと
a_k = \frac{1}{k} \sum_{i=1}^{k} r_i
になります。
次の日、転校生Aさんが来てクラスの人数は11人になりました。Aさんにも直ちにテストを受けてもらったところ432点でした。クラス編成が変わったので新たに平均点を求める必要があります。担任の先生は定義通り計算し直します。生徒が一人増えたので各点数は
185, 348, 419, 407, 250, 323, 364, 355, 389, 359, 432
です。この合計点を生徒の総数11人で割って3831/11 = 348.3点になりました。このように得点が更新されるたびに定義に従って平均点を毎回更新しても良いのですが、例えば人数が1億人になると、得点を格納するメモリのコストも計算量も大きくなります。そこで、前回の平均点と今回新たに追加された得点から新しい平均点を算出するようにしたいと思います。上記の平均点の定義を変形させると
\begin{align}
a_{k+1} &= \frac{1}{k+1} \sum_{i=1}^{k+1}r_i \\
&= \frac{1}{k+1}(r_{k+1} + \sum_{i=1}^{k}r_i) \\
&= \frac{1}{k+1}(r_{k+1} + k\frac{1}{k}\sum_{i=1}^{k}r_i) \\
&= \frac{1}{k+1}(r_{k+1} + k a_k) \\
&= \frac{1}{k+1}(r_{k+1} + k a_k + a_k - a_k) \\
&= \frac{1}{k+1}(r_{k+1} + (k+1) a_k - a_k) \\
&= a_k + \frac{1}{k+1}[r_{k+1} - a_k]
\end{align}
となります。この式を解読すると
新しい推定値 ← 古い推定値 + ステップサイズ [ 最新の更新データ ー 古い推定値 ] (*)
となっています。つまり、推定値(この場合平均点)を漸進的に更新したい場合、古い推定値に対してある差分を足してあげます。その差分とは、最新の更新データと古い推定値の差にステップサイズパラメータを掛けたものになります。
実際に、値を代入してみましょう
新しい推定値 ← 339.9 + 1/11 * [432 - 339.9]
となります。最新の更新データと古い推定値との差(432-339.9)が正なので平均点を引き上げる作用をします。その作用幅はステップサイズパラメータで規定されます。実際に新しい推定値は348.3点となり、直接平均値を求める方法と一致します。
モンテカルロ法の漸進的な表現
モンテカルロ法では、各状態行動対においてエピソードを何度も経験させ、得られた収益$R$の平均をとることで価値関数($V$もしくは$Q$)の期待値計算を行うのでした。
上記の式(*)の考え方をモンテカルロ法の価値関数更新に当てはめると
$$V(s_{t}) ← V(s_t) + \alpha[R_{t} - V(s_t)] (1)$$
と書くことができます。
ここで$R_{t}$は時刻$t$に対応する実際の収益で、定数$\alpha$はステップサイズ・パラメータを表しています。前述した平均点の例ではステップサイズ・パラメータはサンプルサイズの逆数でしたが、今回は固定値$\alpha$として表しました。この方法を**$\alpha$不変MC**と呼ぶことにします。
漸進的な表現にしましたが、**実際に更新されるデータ$R_{t}$はエピソードの終わりまで待たなくてはなりません。**これが、収益を使わなければならないモンテカルロ法の最大の欠点です。
TD法
そこで、動的計画法のアイデアを拝借します。収益$R_t$の代わりに次のステップでの推定値を用います。第1回で解説した状態価値関数の導入を思い出します。
価値関数V(Q)とはある状態(状態行動対)から方策にしたがった時の収益($R_t= r_{t+1} + r_{t+2} + ...$)の期待値でした。
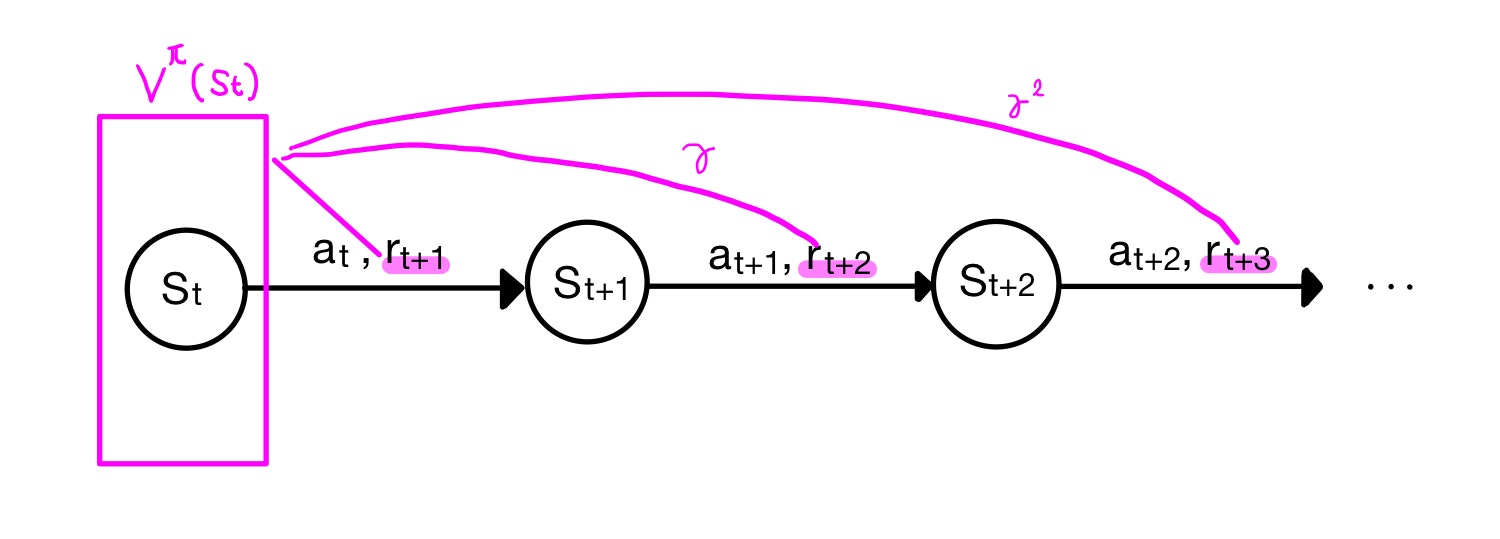
Bellman方程式から、ある状態での価値は、次の状態での価値を用いて表されるのでした。
$$V^\pi(s_t) = r_{t+1} + \gamma V^\pi(s_{t+1})$$
注:実際は次の状態は枝分かれするのでそれらの期待値
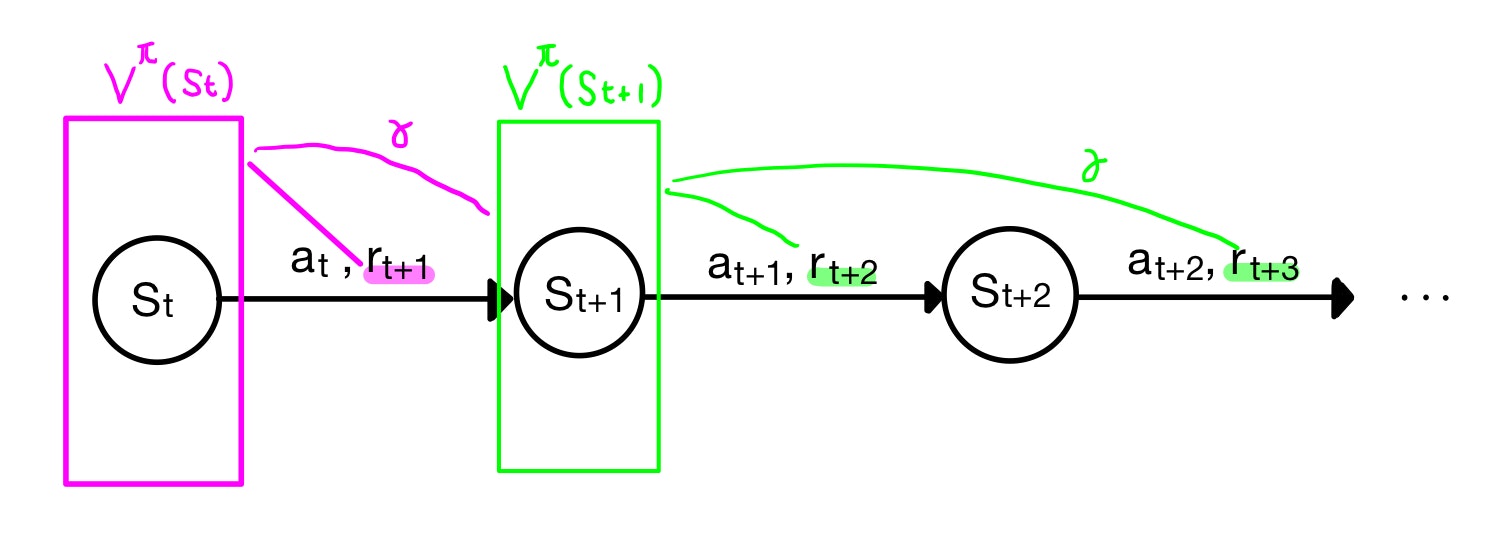
これを用いると、(1)式の収益$R_{t}$をその後に続く報酬$r_{t+1}$と価値関数$V(s_{t+1})$で書き換えることができ、
$$V(s_t) ← V(s_t) + \alpha[r_{t+1} + \gamma V(s_{t+1}) - V(s_t)] (2)$$
となります。結果的に、モンテカルロ法は収益$R_t$を目標として更新するのに対して、TD更新では$r_{t+1} + \gamma V_{t+1}$を目標としています。
TDでは、モンテカルロ法と同じように環境のモデルを知らずともエピソードを進めることで学習を進めます。その際、エピソード終端での収益を待つのではなく、動的計画法のようにブートストラップを用いて(つまり次の状態の推定値を用いて)価値関数の更新を行います。直近の価値関数の推定値を用いるTD法をTD(0)法と呼びます。
TD(0)法による価値関数の推定
初期化:
$\pi \leftarrow$ 評価すべき方策
$V \leftarrow$ 任意の状態価値関数
各エピソードに対して繰り返し:
sを初期化
エピソードの各ステップに対して繰り返し:
a ← sに対して$\pi$で与えられる行動
行動aをとり、報酬rと次状態s'を観測する
$V(s) ← V(s) + \alpha[r + \gamma V(s') - V(s)] $
s ← s'
sが終端状態ならば繰り返しを終了
grid worldの状態価値関数
TD(0)法を用いて[grid world]の状態価値関数を求めてみます。コードはgithubにあります。毎度ですが問題設定は以下。
問題設定
第1回で説明した格子世界
Aにいる状態でどんな行動をとっても+10点、Bも同様に5点。壁にぶつかると-1点、ほかは0点。

for epi in tqdm(range(num_episode)):
delta = 0
i,j = np.random.randint(5, size=2)
agent.set_pos([i,j]) # 移動前の状態に初期化
s = agent.get_pos()
for k in range(num_iteration):
action = ACTIONS[np.random.randint(0,4)]
agent.move(action) # 移動
s_dash = agent.get_pos() # 移動後の状態
reward = agent.reward(s, action)
V[s[0],s[1]] = V[s[0],s[1]] + ALPHA*(reward + GAMMA*V[s_dash[0], s_dash[1]] - V[s[0],s[1]])
s = agent.get_pos()
アルゴリズム通りに実装しています。シンプルですね。
今回、ステップサイズ・パラメータ$\alpha$は0.01としています。このパラメータを大きくすると更新量が大きくなりすぎて価値関数の更新が振動してしまいます。かといって小さすぎると十分な更新がなされないため、エピソード数に対して段々と$\alpha$を減少させていく手法もよく取られます。そうなるともはや$\alpha$不変ではないですね。
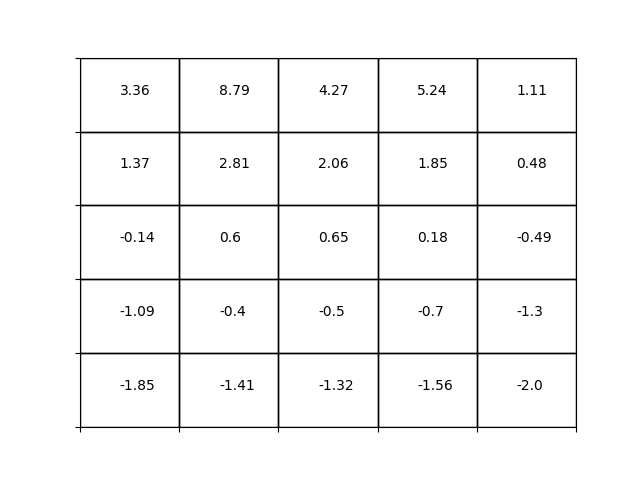
得られた状態価値関数を示します。DP法やMC法と同じく価値関数を精度よく推定できています。
終わりに
今回はTD法の導入と、状態価値関数の推定をおこないました。次の記事では、TD法を用いた制御(最適方策の獲得)を説明します。sarsa法およびQ-learningを実装し、相違点を述べます。