Bancor Protocol

価格決定方程式

Connector Weight

Bancor Protocolは、手元にある資本準備金(balance)を使って、そのトークンの価値を保証し、トークンの新規発行、廃棄をスマートコントラクトで自動化したプログラムである。
はじめに、トークンの時価総額のうちのどのくらいの割合をReseve(depositまたは、connector balance) $R$[eth]として蓄えておくかについてのべる。この割合は、Bancorの中で唯一の定数で固定準備率(fractional reserve ratio) $F$ と呼ばれ、トークンの発行元がはじめに設定できる。この値を一定に保ちながらトークンの価格 $P$[eth]や発行数(供給量) $S$ が価格方程式に基づき決まり、スマートコントラクトによって売買が行われる。上の定義から、トークンの時価総額(Smart Token’s total value)は、

\mbox{Total value} = PS
\tag{1}

であるので、reserve $R$ は、

R=(固定準備率)\times(トークンの時価総額)=FSP
\tag{2}

で決まる。

価格決定方程式

上の(2)式をトークンの価格 $P$ についてとくと、

P=\frac{R}{FS}
\tag{3}

を得る。
この式は、市場の原理にしたがっていて、需要が増える、すなわちそのトークンに蓄えられているreserve $R$[eth] が増えるとき、そのトークンの価格が上がり、供給 $S$ が増える価格が下がることを表している。このように、スマートトークンの価格は(3)式によって決まる。(今回は簡単のためにparent currencyをethだとして単位をつけています。以下では断りがない限りparent currencyはethだと思い計算を行う。)

また、方程式(2)はいわゆる自己無頓着方程式(セルフコンシステント)のような形をしている。
具体的には、reserveの価格は、現在のトークンの価格から計算されるので、$R$はPに依存して決まる。

P=f(P)

価格Pの供給発展

上の(3)式を $P$ 関して完全に解くと、あるsupplyのときにトークンの価格がどのような値になるかを求まる。(supplyを変化させた時にreserveがどれくらい変化するかを求めたいが、価格も同時に変化するのでこの変化が無視できるような微小量の変化を考えることで解くことができる。そこで以下では、微小量で計算を進める)

買い手が新しくスマートトークン微小量購入するときを考えよう。このとき、supply $S$ から微小量$dS$だけ増えた $S+ dS$になったとする。この微小量のスマートトークンを発行するために買い手は、このときのスマートトークンの価格とトークンの量 $dS$ をかけた額のethをdepositすることになる。したがって、reserveの増加量 $dR$ は、

dR=PdS \tag{4}

である。一方、(2)式より、$dR$は、全微分で求まり、$F$ が定数のことに注意すれば、

dR=F d(SP)=FdSP+FSdP \tag{5}

を得る。以上(4),(5)式より、

PdS(1-F)=FSdP

これは、変数分離型の微分方程式なので簡単に解けて、

P=CS^{\frac{1-F}{F}}

となる。ただし、$C$ は積分定数で初期条件として、supply $S_0$ の時に価格を$P_{0}$であるとすると、

P=\bigg(\frac{S}{S_0}\bigg)^{\frac{1-F}{F}}P_0
\tag{6}

と最終的にあるsupply $S$ におけるトークンの価格がもとまった。
この式を元に、様々なConnector Weight(CW) $F$ でその発展を図示すると、以下のようになる。

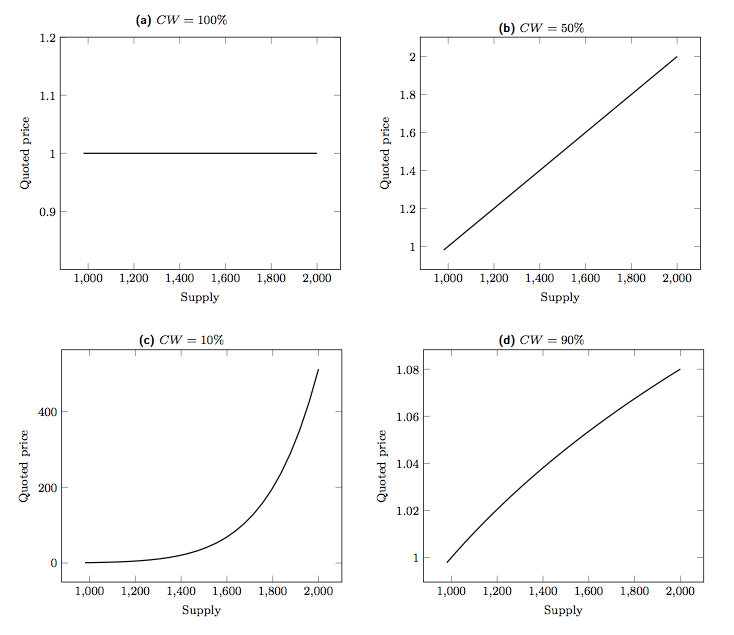
ちなみ、これらを一つのグラフに書き込むと、以下のようになる。この図は、トークンの初めの価格を1ethとして設定し、それ以降有効なグラフである。(初めの交点よりも左側が正しい)定性的には、以下のうように説明できる。$CW=1$の場合は、常にdepositされたethと同等の市場価値になるように調整される。したがって、トークンの価格は、ethの価格と同じになることになる。(30[eth]depositすると市場価値は、30[eth]上がる。)
したがって、トークンの価値もethに対して一定である。一方、$CW$が1から小さくなると、depositされたethに対して、それよりも大きな市場価値がつくことになる。例えば、$CW=0.1$のとき、30[eth]depositすると、市場価格は、300[eth]増加することになる。このため、supplyも低くすみ価格は大きく変化することになる。

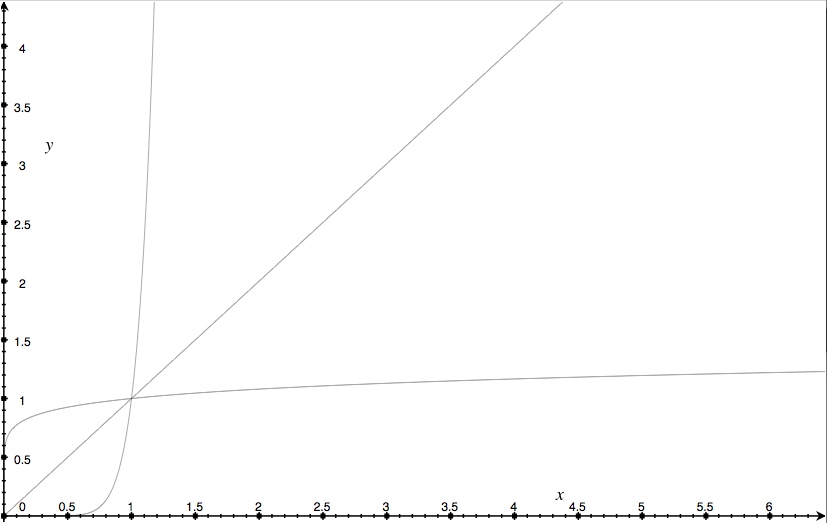
最後に、supplyが$S_0$ のときにスマートトークンをT[BNT]だけ買った場合、どの程度のEthが必要になるかについて求める。必要なEthの量をEで表すと、価格がsupplyとともに、常に変化することに注意すれば、積分、

E=\int^{S_0+T}_{S_0}PdS

によって求まることがわかる。(6)式の結果を用いれば、

E=\int^{S_0+T}_{S_0}\bigg(\frac{S}{S_0}\bigg)^{\frac{1-F}{F}}P_0dS \\
=FS_0P_0\bigg(\sqrt[F]{1+\frac{T}{S_0}}-1\bigg)

が得られる。さらに、$FS_0P_0$は、初めのreserveの値なので、これを$R_0$とすると、最終的に

E=R_0\bigg(\sqrt[F]{1+\frac{T}{S_0}}-1\bigg)
\tag{7}

を得る。さらに、あるEthで購入できるトークンの数が知りたければ、(7)式を $T$について逆解きして、

T=S_0\bigg(\bigg(1+\frac{E}{R_0}\bigg)^{F}-1\bigg)
\tag{8}

と計算される。これらの計算は、スマートコントラクトして取引所など無しに自動で行われている。

結論

今後小さなスケールの経済圏や、youtubeのように個人が通貨を発行し、トークンの市場はロングテールになるだろう。その時、その通貨の流動性を上げるのにbancor Protocolはかなり役に立つだろう。

謝辞

@isseium さんにtypoの指摘をいただき、直させていただきました。ありがとうございます。

Reference

-Eyal Hertzog, Guy Benartzi, Galia Benartzi.Bancor Protocol(white paper)
-Meni Rosenfeld.Formulas for Bancor system
-Bancor プロトコル:Smart Tokenの革新性とは。「Coincidence of Wantsの解決」とそれがもたらす「取引の再発明」
-Why Bancor Will Work?
-Bancor Protocol はトークンエコノミーを支える大発明となるか？（前後編)
-Crypto Note
-bancor(wiki)