はじめに
前回は、100万円を運用したときの将来の収益を平均と標準偏差から、シミュレーションしました。
今回は、つみたて運用をしたときに、将来の資産額をシミュレーションしていきます。
特につみたてNISAに則って計算を行います。
標準偏差を用いなかったとき
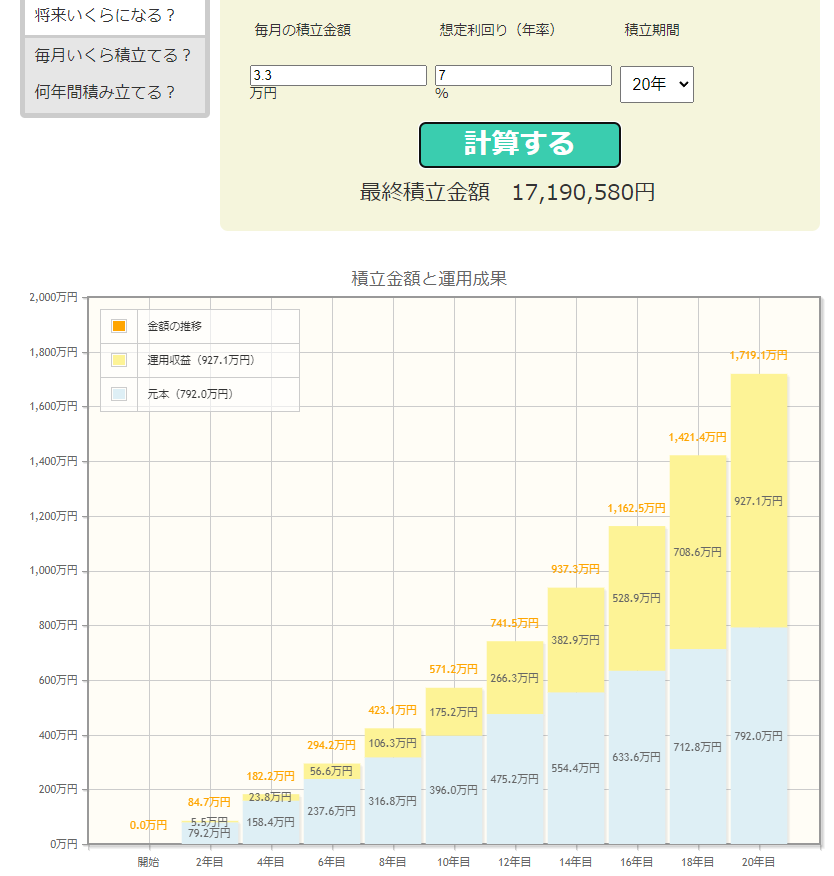
金融庁の資産運用シミュレーションより、
20年後には、つみたてNISAを全くしなかった場合に比べて、2倍になっていますね。
設定
- 年率が平均7.0%、標準偏差25%の正規乱数に従うとする
- 分散投資の意義② 投資のリスクとはより
- 各年の年率は独立試行とする
- 20年間運用するとする
- 100回試算する
code
import numpy
from matplotlib import pyplot
AVERAGE_0 = 0.07
SIGMA_0 = 0.25
# AVERAGE_0 = 0.10
# SIGMA_0 = 0.14
TUMITATE = 40
priceLastArray = []
ax = pyplot.figure().add_subplot(211)
for indtest in range(100):
ganpon = [tumitate]
moneyTotal = [tumitate]
for indYear in range(30):
nenritsuRand = numpy.random.normal(AVERAGE_0,SIGMA_0)
if nenritsuRand < -1:
nenritsuRand = -1+0.0000001
# 株価が0になる(滅亡END)
moneyTotal.append(moneyTotal[-1] * (1.0+nenritsuRand) + TUMITATE)
ganpon.append(ganpon[-1] + TUMITATE)
if indtest < 10:
pyplot.plot(moneyTotal)
priceLastArray.append(moneyTotal[-1])
pyplot.plot(ganpon)
pyplot.yscale("log")
ax.set_xlabel('year')
ax.set_ylabel('price')
ax = pyplot.figure().add_subplot(212)
pyplot.hist(priceLastArray,bins=numpy.logspace(0,5,30))
ax.set_xscale("log")
ax.set_xlabel('price')
ax.set_ylabel('num')
print(f"ganpon:\t{ganpon[-1]:.0f}")
print(f"ave:\t{numpy.average(priceLastArray):.0f}")
print(f"med:\t{numpy.median(priceLastArray):.0f}")
print(f"max:\t{numpy.max(priceLastArray):.0f}")
print(f"min:\t{numpy.min(priceLastArray):.0f}")
print(f"std:\t{numpy.std(priceLastArray):.0f}")
countUnder = 0
for prc in priceLastArray:
if prc < ganpon[-1]:
countUnder+=1
print(f"ganponware:{countUnder/len(priceLastArray)*100}%")
一回試算してみた
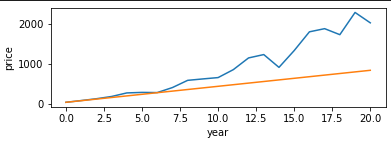
元本840万円をつぎ込んで、合計2026万円です。金融庁シミュレーション結果と近いですね。
100回試算してみた

※上のグラフは100回中10回のみ表示しています。
いやぁ、ばらつきが大きいですね。
最悪400万円、最高7000万円という結果でした。
運よく行けば、ほぼ億万長者ですね!!
平均が1797万円でしたが、これは値の大きい方にばらついてるので、あまり参考にならないです。
中央値1430万円が最もよく起こり得ると考えていいのではないでしょうか。
金融庁の結果にも近いですね。
元本割れしたケースは20%でした。海外株式はリスクが大きい(めっちゃ減ることもめっちゃ増えることも多い)ですね。
ave: 1797
med: 1430
max: 6900
min: 400
std: 1199
ganponware:20.0%
30年運用だと
運用期間だけ30年に伸ばしてみました。

すると、億超えが5%になっています!
5%なら夢がありますよね。
考察
- 株価の変化が正規分布に従うとは考えにくい
- キャピタルゲインとインカムゲインがある
- 各年の株価の変化が独立試行というのも現実に即していない
結論
年率7%でも高リスクになることがわかりました。
高リスク高リターンの商品だと、長期に運用したところで100%安全というわけではないようです。
元本割れのリスクを覚悟がある人だけが、億万長者の可能性をつかめる
ともいえそうです。
逆に、元本割れのリスクの覚悟がないひと、最低ほしい金額が決まっている人は、
より低リスクな金融商品を選ぶべきなのでしょう。
単純な比較はできませんが、一括投資と比べれば長期投資のほうがばらつきが小さくなりました。
長期投資のメリットですね。
次は、確率の観点から、最近話題のFIREの実現可能性を探っても面白いなと思います。
記事書いてほしいですか?