【制御工学】Scilabを使ってナイキスト線図(ベクトル軌跡)を描いてみた！

#概要

制御シミュレーションには，MATLABがよく使われますが，MATLABライクなフリーソフトにScilab(サイラボ)があります．

Scilabであればフリーなので，趣味程度に遊んでみることも気軽にできますし，学生でも使えると思います．（最近は，PythonでもPython-controlを使えば，制御シミュレーションができるので，Python-controlについても機会があれば触れたいと思います．）

一方で，オンラインでの情報が少ないのが欠点かもしれません．今日は，制御で必須のナイキスト線図(ベクトル軌跡)をScilabで描画してみようと思います．

ボード線図についてはこちらにまとめてあります．
https://qiita.com/trami/items/14423f29c394ce5f44b0

#動作環境

• Windows10(64bit)
• Scilab 6.0.2

#ナイキスト線図(ベクトル軌跡)とは
ナイキスト線図，またの名をベクトル軌跡といいます．ナイキスト線図と聞くと，なんか難しそうですが，やっていることは簡単です．周波数伝達関数$G(j\omega)$を複素数平面上に角周波数$\omega$の関数として描画しているだけです．高校の数三で出てきた複素平面です．
じゃあ，ボード線図と何が違うのかというと，本質的にやっていることは同じです．ただ，使う場面が違うと理解しておけばいいでしょうか？ボード線図は，人間でも書くことができ比較的容易に利用できます．一方，ナイキスト線図はものによっては人間だと書くのが難しいです．じゃあ，ボード線図だけでいいじゃないかと．そうゆうわけにはいきません．ナイキスト線図を使えば，安定余裕というものも求められます．安定余裕とは，簡単に言うと，システムが安定をキープするために(不安定になってしまう前に)どれだけの余裕があるのかということです．もちろん安定余裕をボード線図から求めることもっできますが，ナイキスト線図を使った方が若干ラクといった感じでしょうか？まあ，この辺については古典制御の参考書がたくさんあるでしょうから，そちらを参考にしてもらった方がよいかもしれません．

#伝達関数の定義
ではまず伝達関数の定義をします．ここはおまじないだと思ってもらって構いません．
伝達関数は仮に

G(s)=\frac{1}{s^2+2s+3}\

としておきます.

s = %s; //記号変数の定義
Gs = 1/(s^2 + 2*s + 3) //伝達関数の定義 
G = syslin('c', Gs); //連続時間システムの定義

#ナイキスト線図の描画
伝達関数の定義ができたので，早速ナイキスト線図(ナイキスト線図)を描画していきたいと思います．
といっても，Scilabであれば一行でナイキスト線図がかけてしまいます．さすがですね．引数の説明をすると，第2引数は周波数の最小値，第3引数は周波数の最大値，第4引数はsymmetry引数といい，デフォルトでは%t(=true)になっており，これを%f(=false)にしないと周波数が負の範囲も描画されてしまうため，%fを指定します．
詳しくは積分要素のところで解説をします．

nyquist(G, 0, 100000, %f)

では様々な要素について復習をしつつ，ナイキスト線図を描画していってみましょう．

##比例要素

G(s) = K

まずは，比例要素．これ自体に解説はいらないと思いますが，Scilabで実行する時には，注意が必要です．以下のようにしてしまうとエラーが出てしまいます．

K = 1;
Gs = K 

syslin: 入力引数 #2 の型が正しくありません: 線形状態空間または伝達関数を指定してください.

正しくは以下のように書きます．

K = 1;
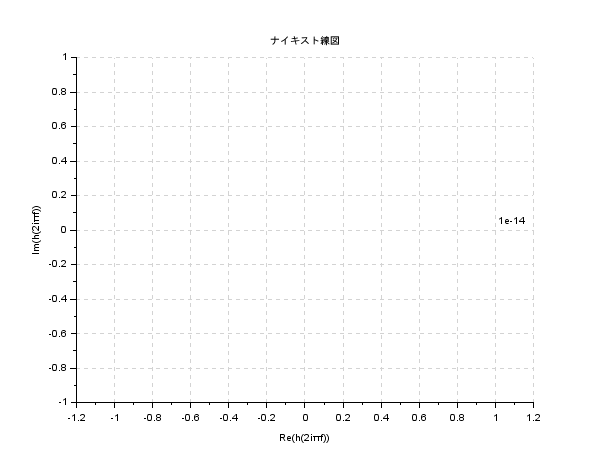
Gs = K / s^0 

おそらくこれは，点が一点なので小さすぎて見えないのではないでしょか？比例定数を変えてみてください．軸のスケールが変わってくることで理解できると思います．

##積分要素

G(s) = \frac{1}{s}\

続いては積分要素です．難しくはないですが大事ですね．

Gs = 1/s  

ここで，以下のようにしてみてください．

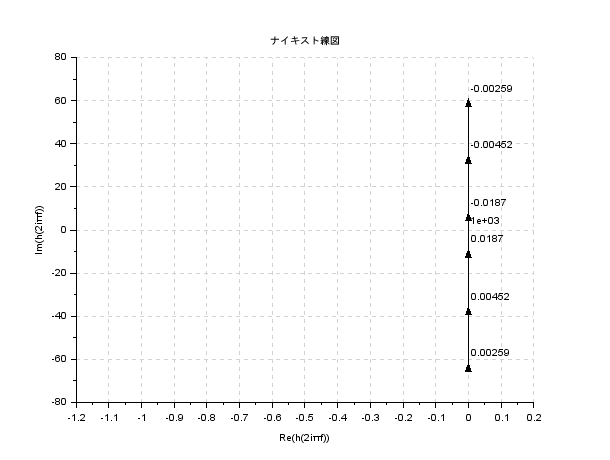
nyquist(G)

おそらく，以下のように表示がされたと思います．

一般的には，ナイキスト線図は，角周波数$\omega$が$0$から$+\infty$を表示するのですが，角周波数$\omega$が$-\infty$から$+\infty$で表示がされてしまっているのです．

ここで次に，nyquist()関数の第2,3引数に値を渡せば，周波数の最小値と最大値が指定できると公式ドキュメントに記述があるので，以下のように変更をしてみます．

nyquist(G, 0, 100000)

しかし，こうしても先ほどと同じまま出力がされると思います．

実はnyquist()関数，symmetry引数というものを取ることができ，これはグラフの対称性を指定する引数になっています．デフォルト(値を指定しない)では，%tとなっており，上下対称のグラフを描く仕様になっています．(この%tはtrueのt)なので，周波数が正の範囲だけを描画させたいときはsymmetry引数をfalseにしてあげる必要があります．具体的には以下のようにします．

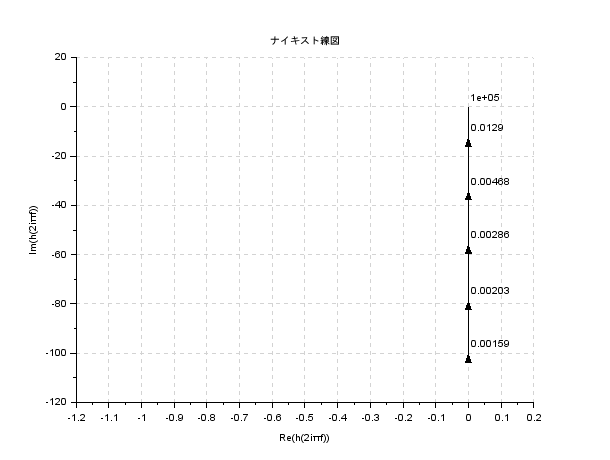
nyquist(G, 0, 100000, %f)

そうすると，以下のような$\omega$が$0$から$10^5$までのナイキスト線図を得ることができます．

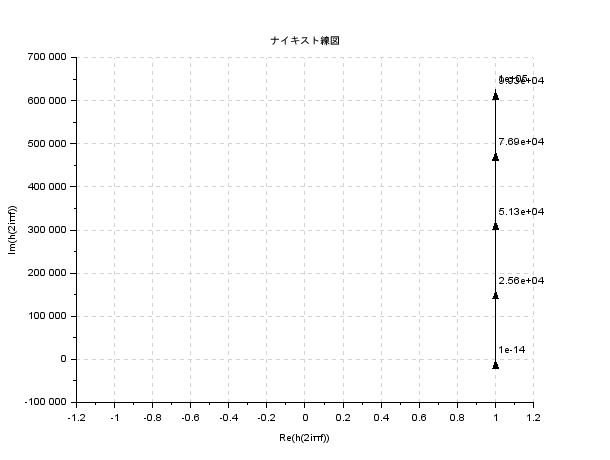
##微分要素

G(s) = s

次は微分要素です．物理的には実現できないのであまり重要ではありませんが，一応挙げておきます．
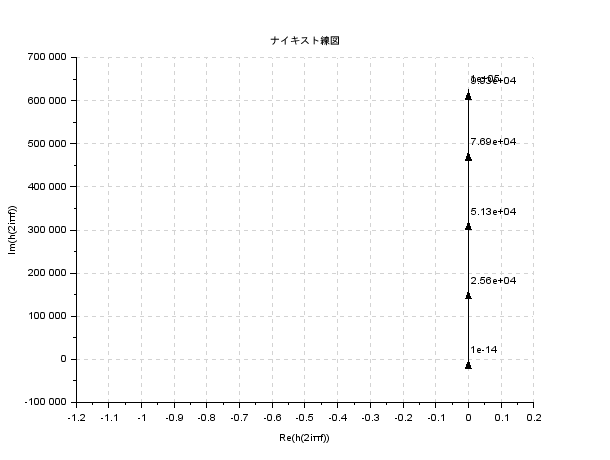
比例要素と同様に分母にs^0を付けるのを忘れないようにしましょう．

Gs = s / s^0

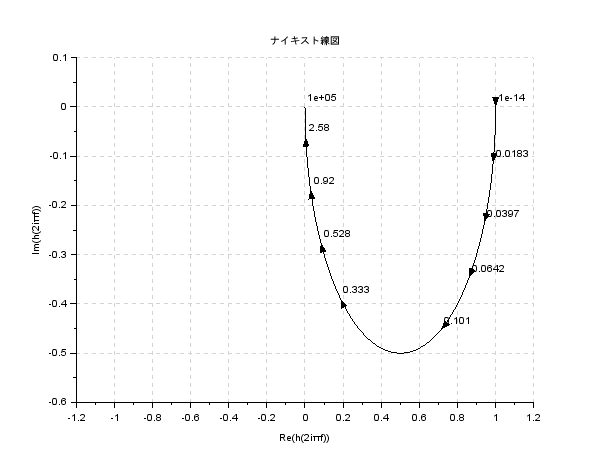
##一次遅れ要素

G(s) = \frac{K}{1+Ts}\

次は一次遅れ要素です．非常に重要ですね．
Kは比例定数，Tは時定数です．RC回路であれば$T=1/CR$，RL回路であれば$T=L/R$となります．また時定数は最終値の$63.2%$に達するまでの時間でした．

T = 1;
K = 1;
Gs = K / (1 + T * s)

##一次進み要素

G(s) = K(1+Ts)

次は一次進み要素です．こちらも微分要素同様あまり重要ではありませんが，挙げておきます．
Kは比例定数，Tは時定数です．

T = 1;
K = 1;
Gs = K * (1 + T*s) / s^0

ボード線図を比べると，一次遅れ要素との対称性がいまいちに思えますね．むしろ微分要素に似ていますね．

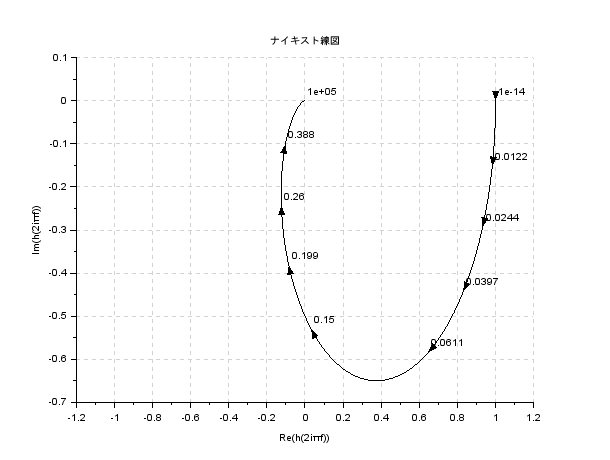
##二次遅れ要素

G(s) = \frac{(\omega_n)^2}{s^2+2\zeta\omega_ns+(\omega _n)^2}\

次は二次遅れ要素です．これも非常に重要ですね．
$\omega_n$は固有角周波数，$\zeta$は減衰定数ですね．

z = 1;
wn = 1;
Gs = 1 / (s^2 + 2*z*wn*s + wn^2)

##むだ時間要素

G(s) = \exp(-Ls)

最後はむだ時間要素です．遅延ですね．

これは，パデ近似を用いる必要があるので，また別の記事でまとめたいと思います．

#まとめ
Scilabを使うととても簡単にナイキスト線図を描くことができました．ナイキスト線図は手計算で描くのが少し難しいのでScilabで確認するとよいのではないでしょうか．
また，ナイキスト線図を使えば安定余裕についても容易にわかるので，安定余裕についてもまとめていきたいと思います．

[ ボード線図 ] https://qiita.com/trami/items/14423f29c394ce5f44b0