【制御工学】Scilabを使ってボード線図を描いてみた！

#概要

制御シミュレーションには，MATLABがよく使われますが，MATLABライクなフリーソフトにScilab(サイラボ)があります．

Scilabであればフリーなので，趣味程度に遊んでみることも気軽にできますし，学生でも使えると思います．（最近は，PythonでもPython-controlを使えば，制御シミュレーションができるので，Python-controlについても機会があれば触れたいと思います．）

一方で，オンラインでの情報が少ないのが欠点かもしれません．今日は，制御で必須のボード線図をScilabで描画してみようと思います．

ナイキスト線図についてはこちらにまとめてあります．
https://qiita.com/trami/items/9fd130779fc0e0adc1bf

#動作環境

• Windows10(64bit)
• Scilab 6.0.2

#ボード線図とは
ボード線図とは，周波数伝達関数のゲインと位相を，角周波数ωを横軸とする1組のグラフで表したものです．前者をゲイン線図，後者を位相線図と呼びます．
ゲイン線図の縦軸は$20\log_{10}|G(j\omega)|$を単位デシベル(dB)で，位相線図の縦軸は位相${\angle}G(j\omega)$を単位(°)で表示します．また，横軸は角周波数$\omega$を対数軸目盛$\log_{10}\omega$上に取り，広い範囲の$\omega$を表現できるようにします．

#伝達関数の定義
まずは伝達関数の定義をします．ここはおまじないだと思ってもらって構いません．
伝達関数は仮に

G(s)=\frac{1}{s^2+2s+3}\

としておきます.

s = %s; //記号変数の定義
Gs = 1/(s^2 + 2*s + 3) //伝達関数の定義 
G = syslin('c', Gs); //連続時間システムの定義

#ボード線図の描画
伝達関数の定義ができたので，早速ボード線図を描画していきたいと思います．
といっても，Scilabであれば一行でボード線図がかけてしまいます．さすがですね．

bode(G)

では様々な要素について復習をしつつ，ボード線図を描画していってみましょう．

##比例要素

G(s) = K

まずは，比例要素．これ自体に解説はいらないと思いますが，Scilabで実行する時には，注意が必要です．以下のようにしてしまうとエラーが出てしまいます．

K = 1;
Gs = K 

syslin: 入力引数 #2 の型が正しくありません: 線形状態空間または伝達関数を指定してください.

正しくは以下のように書きます．

K = 1;
Gs = K / s^0 

Scilabで実行すると，上記のボード線図が得られます．これはオールパスフィルタ(全域通過フィルタ)ですね．
ここで1つ注意点ですが，Scilabでは横軸が角周波数$\omega$ではなく，周波数$f$で表示がされます．角周波数に変換することもできるのですが，副作用が大きいのであまりオススメはしません．

ちなみに完全に余談ですが，ScilabではC言語と違って文末のセミコロン(;)をつけなくてもエラーは出ません．(コンソールに多少の違いはありますが…)

##積分要素

G(s) = \frac{1}{s}\

続いては積分要素です．難しくはないですが大事ですね．

Gs = 1/s  

抑えておきたい点は2つですね．

• ゲイン線図の傾きは$-20$dB/dec
• 位相線図は$90^{\circ}$遅れ

ここでdecはdecadeの略でデカードと読みます．これはローマ字読みに由来するのでしょうか？英語ではディケイドと発音しますね．(仮面ライダーディケイドとかありましたね！)

積分器1つで$-20$dB/dec，$90^{\circ}$遅れ．
では，積分器2つでは？？

もちろん$-40$dB/dec，$180^{\circ}$遅れ．となりますね．

##微分要素

G(s) = s

次は微分要素です．物理的には実現できないのであまり重要ではありませんが，一応あげておきます．
比例要素と同様に分母にs^0を付けるのを忘れないようにしましょう．

Gs = s / s^0

積分器と全くの逆の挙動になりますね．

• ゲイン線図の傾きは$20$dB/dec
• 位相線図は$90^{\circ}$進み

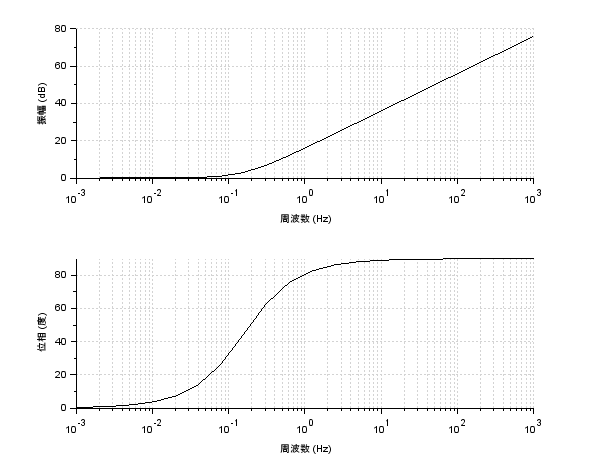
##一次遅れ要素

G(s) = \frac{K}{1+Ts}\

次は一次遅れ要素です．非常に重要ですね．
Kは比例定数，Tは時定数です．RC回路であれば$T=1/CR$，RL回路であれば$T=L/R$となります．また時定数は最終値の$63.2%$に達するまでの時間でした．

T = 1;
K = 1;
Gs = K / (1 + T * s)

抑えておきたい点はたくさんありますね．

• 折れ点は$\omega＝2{\pi}f=T^{-1}$のところ
• 折れ点ではゲインが$-3$dB
• 高周波でのゲイン線図の傾きは$-20$dB/dec
• 位相線図は折れ点で$45^{\circ}$遅れ
• 比例要素と積分要素で折れ線近似できる
• 低域通過フィルタとして機能する

##一次進み要素

G(s) = K(1+Ts)

次は一次進み要素です．こちらも微分要素同様あまり重要ではありませんが，挙げておきます．
Kは比例定数，Tは時定数です．

T = 1;
K = 1;
Gs = K * (1 + T*s) / s^0

これは一次遅れ要素と逆の挙動になりますね．

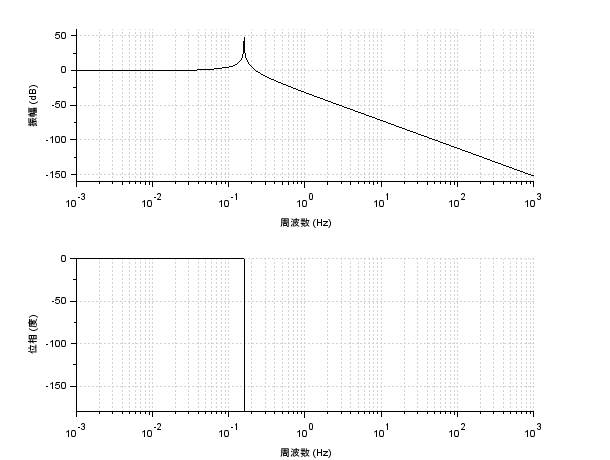
##二次遅れ要素

G(s) = \frac{(\omega_n)^2}{s^2+2\zeta\omega_ns+(\omega _n)^2}\

次は二次遅れ要素です．これも非常に重要ですね．
$\omega_n$は固有角周波数，$\zeta$は減衰定数ですね．

では，減衰係数を0,1に対してボード線図を描いてみます．減衰係数は実際は正の値ですが，今は理想的に0としてみます．

z = 1;
wn = 1;
Gs = 1 / (s^2 + 2*z*wn*s + wn^2)

z = 0;
wn = 1;
Gs = 1 / (s^2 + 2*z*wn*s + wn^2)

抑えておきたい点はたくさんありますね．

• 折れ点は$\omega＝2{\pi}f=w_n$のところ
• 高周波でのゲイン線図の傾きは$-40$dB/dec
• 位相線図は折れ点で$90^{\circ}$遅れ
• 折れ点付近で共振が観測される．
• 減衰係数が$1/\sqrt{2}\sim0.707$より小さいと$0$dBを超える
• 減衰係数が小さいほどピークは鋭くなる

##むだ時間要素

G(s) = \exp(-Ls)

最後はむだ時間要素です．遅延ですね．

これをScilabで描こうとしたのですがエラーが出てしまいました．もしかすると，指数関数は線形ではないからかもしれません．パデ近似なるものを用いる必要があるのかもしれませんが，筆者には力不足なのでわかり次第追記という形にしたいと思います．
[追記2019.6.11]
やはり，むだ時間要素は線形ではないため，そのまま描画することはできないようです．他のサイトでは誤魔化してあったりして悩んでしまったので，もう一度はっきり書いておきます．

Scilabではむだ時間要素は線形ではないため，直接描画することはできません！

むだ時間要素を描画したいときは，パデ近似というものを使って，伝達関数を多項式に近似する必要があります．このパデ近似ですが，MATLABではパデ近似のための関数pade()があるのですが，Scilabではないようです．
パデ近似についてはまた時間があるときにまとめたいと思います．

#まとめ
Scilabを使うととても簡単にボード線図を描くことができました．ボード線図であれば計算機を使わなくても比較的描きやすいですが，確認するにはちょうどいいのではないでしょうか．次は計算機なしでは描画が難しいナイキスト線図や安定余裕などについてまとめていきたいと思います．

[ ナイキスト線図 ] https://qiita.com/trami/items/9fd130779fc0e0adc1bf