0. 概要

MultiHeadAttentionとは入力データの変換器のようなものです。モデルの学習のために入力データの重要な部分を際立たせる感じです。Attentionがその際立たせるという意味のどこに注目するかで、MultiHeadとはその変換器のようなものが複数あって、それぞれをヘッドと呼んでいて、その総和で1つの変換器を完成させるという意味です。
そしてこの記事は、自然言語処理や画像処理でも利用されているTransformerなどでもその内部で用いられるMulti-Head Attentionについて理解することを目的としています。
理解するための方法としては、ライブラリになっているtf.keras.layers.MultiHeadAttentionの計算を手動で再現することにより計算方法を確認していきます。
そしてさらにattention scoresと呼ばれる入力データのどこを注目するのかを可視化することによりAttentionの効果をみていきます。

↓ MultiHeadAttentionの論文からの引用で、右側が Multi-head attentionの構造を示すもの。左側はその一部のScaled Dot-Product Attentionを示すものです。

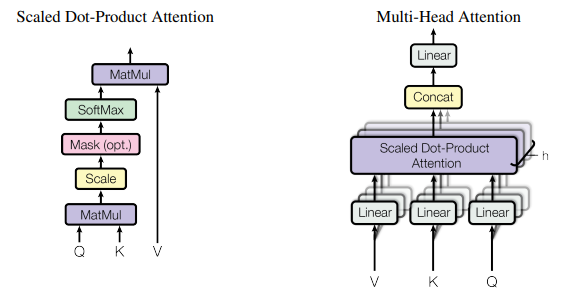
1. MultiHeadAttentionの計算の概要

入力は3つあります。

query: 機械学習に使用したい入力データです。このデータが変換されます。
key: queryとある関係を持つデータです。例えば関係が「類似性」ならば、queryとkeyがどれだけ似ているのかが最初に計算されます。
value: 変換の元データです。queryとkeyの関係性が求められた後で、その関係性に従ってvalueが変換されてqueryの代わりになります。例えばqueryとkeyのデータで2番目の位置のデータが似ているならば、valueの2番目のデータが大きくなってqueryの代わりになります。

query, key, valueを同じデータを指定するとself-attentionと呼ばれます。この記事では以降は、このself-attentionについて記述していきます。

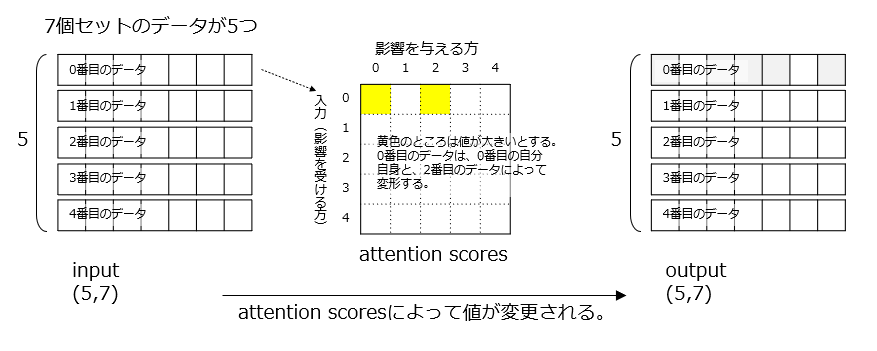
例えば入力データが(5,7)次元のデータとします。上記の図の例だと、7個セットのデータが5個つながっているという感じです。文字列データとしてみる場合、1文字が7要素のベクトルでエンコードされて、5文字で構成されているとみることができます。

Attentionの機構は大まかにいうと上図のattention scoresを学習データから求めて、そのattention scoresで入力データを変換します。attention scoresは入力データが(5,7)次元なら5×5の行列です。行が影響を受ける方、列が影響を与える方に相当し、例えば上記の黄色い部分の数値が大きいならば、入力データの0番目は、自分自身のデータだけでなく2番目のデータからも影響を受けて値が変更されるという感じです。

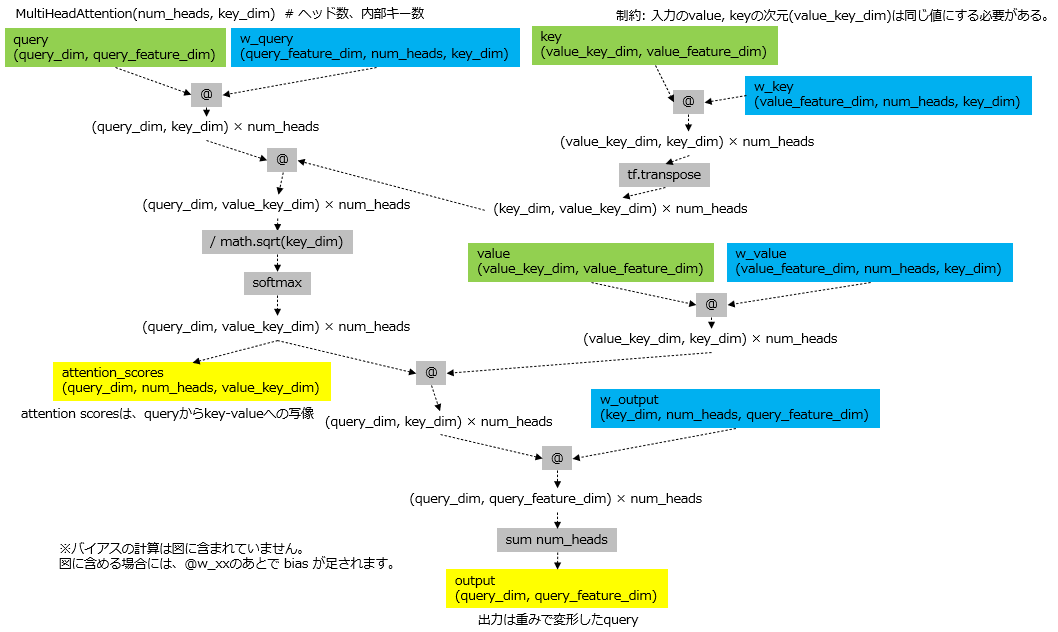
MultiHeadAttention内のパラメータを含めて計算過程を示すと上のようになります。入力は緑色の query, value, keyの3つのテンソルです。出力は、MultiHeadAttentionの実行時の引数であるreturn_attention_scoresをTrueにするとMultiHeadAttentionの出力とattention scoresの2つの図では黄色のところが返ります。MultiHeadAttentionのパラメータである重みは4種類あり、図では青で囲まれています。

@は行列の積を表します。tf.matmulと同じでpython 3.5から実装された機能です。詳細はここに示されています。

各パラメータに付随するバイアスは記載されていません。バイアスは、@ によって行列の積が求められた後で足される値のことです。

2. MultiHeadAttentionの主要な引数

引数はMultiHeadAttentionレイヤーの生成時と、実行時の2つに分かれます。

生成時
- num_heads: ヘッド数、提案論文では 6 が用いられている。kerasのMultiHeadAttentionの場合、同じ入力データをすべてのヘッドが受け取るので、ヘッド数が多いと単に入力に適用するフィルター数が多くなるのと同じになります。よって例えば入力データにn種類の特徴があると想定される場合、n以上のヘッド数を指定すると良いことになります。ここで「n以上」であり「n」ではないのは、各ヘッドの重みの初期値によって同じ特徴を複数のフィルタが捕えようとしてしまい、結果的にn個の特徴を網羅できないことを防ぐためです。
- key_dim: MultiHeadAttentionの内部状態の次数です。入力のkeyのことではありません。これはRNNなどの時系列ニューラルネットワークの内部状態と同じで、モデルが表現できるものの複雑さを表します。多いほど細かくモデル化できますが計算コストがかかるとの過学習のリスクが大きくなります。
実行時
- query: 入力データです。最終的にMultiHeadAttentionは、このデータの中で重要な部分が強調されて出力されるというイメージです。
- value, key: key-valueのセットで、keyがqueryとの関係を保持し、その関係に従ったvalueでqueryが上書きされます。keyは省略可能で、省略するとvalueがkeyの役割も担います。またvalueにqueryと同じデータを渡すと、query = value = keyとなりself-attentionの形式となります。
- return_attention_scores: attention scoresの出力も行います。attenion scoresは、queryとkeyの関係を表すもので関係が類似度ならば似ている箇所を示す行列となります。

3. プログラムの実行環境、準備とバージョン確認

Google Colaboratoryを使用します。

環境の準備とバージョンの確認

# 日本語のmatplotlib環境をインストール
!pip install japanize-matplotlib

# 各種のライブラリ
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
import numpy as np
import math
import matplotlib
import matplotlib.pyplot as plt
import japanize_matplotlib

# 各種のバージョンを確認する
!python --version
print(f"numpy {np.__version__}")
print(f"tensorflow {tf.__version__}")
print(f"matplotlib {matplotlib.__version__}")

実行結果の一部

...
Successfully installed japanize-matplotlib-1.1.3
Python 3.9.16
numpy 1.22.4
tensorflow 2.11.0
matplotlib 3.7.1

この記事を作成時点での各ライブラリのバージョンです。

4. 入力データの作成

入力データの作成

# 総データ数
BATCHES = 1

# データは、(SEQS,CHANNELS)形式とする。
# 時系列データならSEQS個の時系列で、1つのデータはCHANNELS個から形成されているとみる。
# 1次元画像データならSEQS個の画素で、1つの画素はCHANNELS要素数で構成されているとみる。
SEQS = 5
CHANNELS = 7

# 入力データはランダムに生成する。
train_x = np.random.rand(BATCHES,SEQS,CHANNELS)
print(f"train_x{train_x.shape}")
print(train_x)

出力例（乱数を使用しているので実行ごとに数値は異なります）

train_x(1, 5, 7)
[[[0.32490158 0.26017812 0.3843023  0.63927893 0.4235233  0.83661656
   0.54849799]
  [0.22851862 0.04903531 0.79121702 0.70757607 0.60107354 0.17142953
   0.70487199]
  [0.43194427 0.34158653 0.05071445 0.29810708 0.01803537 0.21140811
   0.96329884]
  [0.15951015 0.08968837 0.36834354 0.33316869 0.20606587 0.13913092
   0.26996403]
  [0.39782641 0.581368   0.87842127 0.46452592 0.58710279 0.13579005
   0.45399937]]]

7要素でできているデータが5つ並ぶという(5,7)次元のデータとします。これがバッチ数分だけあるという扱い方をします。まず計算過程をみるので、バッチ数を1にしています。値はランダムに決定されます。

5. 機械学習モデルの構築

機械学習モデルの構築

# ヘッドの数
HEADS = 3

# MultiHeadAttentionの内部状態の次元数
KEY_DIM = 8

# モデルの構築
inputs = layers.Input(shape=(train_x.shape[1:]))
x = inputs
x, att_scores = layers.MultiHeadAttention(num_heads=HEADS,key_dim=KEY_DIM)(x,x,return_attention_scores=True)
model = keras.models.Model(inputs=inputs,outputs=[x,att_scores])
model.summary()

出力例

Model: "model"
__________________________________________________________________________________________________
Layer (type)                   Output Shape         Param #     Connected to
==================================================================================================
input_1 (InputLayer)           [(None, 5, 7)]       0           []

multi_head_attention (MultiHea  ((None, 5, 7),      751         ['input_1[0][0]',
dAttention)                     (None, 3, 5, 5))                 'input_1[0][0]']

==================================================================================================
Total params: 751
Trainable params: 751
Non-trainable params: 0
__________________________________________________________________________________________________

機械学習モデルはMultiHeadAttentionレイヤーだけから構成されています。

6. kerasのMultiHeadAttentionによるattention scoresと出力の計算

# モデルにより計算する。
att_output, att_scores = model.predict(train_x)

# 入出力データの表示
print(f"input{train_x.shape}   -----------")
print(train_x)
print()
print(f"att_output{att_output.shape}  -----------")
print(att_output)
print()
print(f"att_scores{att_scores.shape} -----------")
print(att_scores)
print()

出力例

1/1 [==============================] - 1s 538ms/step
input(1, 5, 7)   -----------
[[[0.32490158 0.26017812 0.3843023  0.63927893 0.4235233  0.83661656
   0.54849799]
  [0.22851862 0.04903531 0.79121702 0.70757607 0.60107354 0.17142953
   0.70487199]
  [0.43194427 0.34158653 0.05071445 0.29810708 0.01803537 0.21140811
   0.96329884]
  [0.15951015 0.08968837 0.36834354 0.33316869 0.20606587 0.13913092
   0.26996403]
  [0.39782641 0.581368   0.87842127 0.46452592 0.58710279 0.13579005
   0.45399937]]]

att_output(1, 5, 7)  -----------
[[[-0.01935837  0.23451312  0.04786216 -0.31212133  0.18013415
    0.25537926  0.17586923]
  [-0.02007195  0.2341773   0.0485854  -0.312371    0.18114641
    0.2551632   0.1763657 ]
  [-0.0195642   0.23460469  0.04772483 -0.3120007   0.18077153
    0.2545155   0.17425014]
  [-0.02060139  0.23423262  0.04830268 -0.31204015  0.182181
    0.25510603  0.17550144]
  [-0.019925    0.23400596  0.04858266 -0.31262937  0.18083808
    0.25478742  0.17601013]]]

att_scores(1, 3, 5, 5) -----------
[[[[0.20107314 0.20571849 0.19305588 0.20196906 0.19818346]
   [0.19956116 0.206497   0.19219774 0.2022371  0.19950701]
   [0.19852804 0.20093425 0.19843031 0.199238   0.20286933]
   [0.19982982 0.2025421  0.19619405 0.2011461  0.20028795]
   [0.19893743 0.20526461 0.19141008 0.20293026 0.20145765]]

  [[0.20234194 0.19659589 0.20314568 0.19938874 0.19852774]
   [0.20439057 0.19854018 0.19828096 0.19882214 0.19996612]
   [0.1981504  0.1989781  0.20315565 0.20173123 0.19798459]
   [0.2019667  0.19963577 0.19904017 0.19913687 0.20022044]
   [0.20230423 0.200125   0.19915625 0.19755708 0.2008574 ]]

  [[0.20181927 0.19517542 0.20552881 0.20081246 0.19666404]
   [0.20416309 0.19777557 0.2002391  0.20127144 0.19655083]
   [0.19733332 0.19420035 0.20823859 0.20359878 0.19662902]
   [0.20185941 0.19888419 0.2001838  0.20064123 0.19843134]
   [0.20559046 0.19726498 0.20071685 0.2004946  0.19593315]]]]

モデルのパラメータは初期値のままで入力データのtrain_xを入れて出力とattention scoresを求めます。次のこの値と同じ値を計算する方法を手動で作成します。

7. MultiHeadAttentionの重みの形状を表示

まず手動での計算の前に、MultiHeadAttentionレイヤーのパラメータの形状を確認します。

MultiHeadAttentionの重みの形状を表示

# index=1にあるMultiHeadAttentionレイヤの重みを取り出して、名前と形を出力する。
for w in model.layers[1].weights:
  print(f" {w.name}, shape={w.shape}")

出力例

multi_head_attention/query/kernel:0, shape=(7, 3, 8)
multi_head_attention/query/bias:0, shape=(3, 8)
multi_head_attention/key/kernel:0, shape=(7, 3, 8)
multi_head_attention/key/bias:0, shape=(3, 8)
multi_head_attention/value/kernel:0, shape=(7, 3, 8)
multi_head_attention/value/bias:0, shape=(3, 8)
multi_head_attention/attention_output/kernel:0, shape=(3, 8, 7)
multi_head_attention/attention_output/bias:0, shape=(7,)

MultiHeadAttentionはquery, key, valueと名付けられた3つの入力を受け取ります。このそれぞれにkernelと呼ばれる重みがかけられて、biasと呼ばれる数値が足し合わされます。kernelの形状は(入力のchannel数, ヘッド数, key_dim)です。biasは(ヘッド数, key_dim)です。key_dimは、入力のkeyの次元ではなくMultiHeadAttentionの内部状態の次元数です。大きな次元数ほど内部の表現が複雑になります。そしてquery,keyから求められたattention scoresとvalueをかけて作られたテンソルに出力用のパラメータがかけられます。出力用のkernelの次元は(ヘッド数, key_dim, 入力のchannel数)、biasは(入力のchannel数)です。

この計算によって出力は、入力のqueryと同じ次元となります。attention scoresは、(ヘッド数, queryのシーケンス数, key/valueのシーケンス数)です。keyとvalueのシーケンス数は同じ値にする必要があります。

8. 手動でMultiHeadAttentionの出力とattention socresを計算する

手動でMultiHeadAttentionの出力とattention socresを計算する

# query, key, value, batch_sizeは1固定
q = k = v = train_x[0]

# MultiHeadAttentionレイヤの重みを、各変数に代入する。
w_q = model.layers[1].weights[0:2] # queryにかける重み
w_k = model.layers[1].weights[2:4] # keyにかける重み
w_v = model.layers[1].weights[4:6] # valueにかける重み
w_o = model.layers[1].weights[6:8] # 出力にかける重み

# 
print(f"query,key,value:{q.shape}")
print(f"w_q_0(kernel):{w_q[0].shape}, w_q_1(bias):{w_q[1].shape}")
print(f"w_k_0(kernel):{w_k[0].shape}, w_k_1(bias):{w_k[1].shape}")
print(f"w_v_0(kernel):{w_v[0].shape}, w_v_1(bias):{w_v[1].shape}")
print(f"wo_0(kernel):{w_o[0].shape}, wo_1(bias):{w_o[1].shape}")

# MultiHeadAttentionレイヤの実装はeinsum(アインシュタインの縮約記法)
# を用いて一度に計算しているが、理解しやすくするためにここでは
# ヘッドごとに分けて計算する。
for head in range(HEADS):
  # queryとkeyのlinear transformation
  qw = q @ w_q[0][:,head,:] + w_q[1][head,:]
  kw = k @ w_k[0][:,head,:] + w_k[1][head,:]

  # scaled dot production
  kw_t = qw @ tf.transpose(kw) / math.sqrt(KEY_DIM)

  # softmax
  _att_scores = tf.nn.softmax(kw_t)

  # 手動計算の_att_scoresと、モデルによる計算のatt_scoresをそれぞれ出力する。
  print(f"calculated attention score head{head}---------------------")
  print(_att_scores)
  print(f"original attention score head{head} ---------------------")
  print(att_scores[0,head])
  print()

# attention outputの手動計算をヘッドごとに行い、その結果を保持する。
_att_outputs = []
for head in range(HEADS):
  # valueのlinear transformation
  vw = v @ w_v[0][:,head,:] + w_v[1][head,:]
  # attention scoreとの掛け算（ここではモデルが出力するattention scoreを用いる）
  av = att_scores[0,head] @ vw
  # 出力を保存する。
  _att_outputs.append(av @ w_o[0][head] + w_o[1])

# 各ヘッドごとの出力は sum によって合計される。
print("calculated attention output ################")
print(sum(_att_outputs))
print("original attention output ################")
print(att_output)

出力例の一部

calculated attention score head0---------------------
tf.Tensor(
[[0.20107314 0.20571849 0.19305588 0.20196906 0.19818346]
...
original attention score head0 ---------------------
[[0.20107314 0.20571849 0.19305588 0.20196906 0.19818346]
...
...
calculated attention output ################
tf.Tensor(
[[-0.01935838 0.23451313 0.04786214 -0.3121213 0.18013413 0.25537926
...
original attention output ################
[[[-0.01935837 0.23451312 0.04786216 -0.31212133 0.18013415
...

各ヘッドごとに計算しています。kerasの実装ではアインシュタインの縮約記法を用いてヘッドごとにループせずに一度に計算をしていますが、ここでは分かりやすくするためにヘッドごとにループしてそれぞれの値を求めています。

まずヘッドごとの出力をオリジナルのkerasライブラリからの出力と比較し、そして最後にヘッドごとの出力を合計したMultiHeadAttention自体の出力をkerasライブラリと比較しています。どちらも計算の誤差でピッタリとは合っていませんがほぼ問題なく計算できています。

出力例の全体を確認する場合はここを開いてください。

query,key,value:(5, 7)
w_q_0(kernel):(7, 3, 8), w_q_1(bias):(3, 8)
w_k_0(kernel):(7, 3, 8), w_k_1(bias):(3, 8)
w_v_0(kernel):(7, 3, 8), w_v_1(bias):(3, 8)
wo_0(kernel):(3, 8, 7), wo_1(bias):(7,)
calculated attention score head0---------------------
tf.Tensor(
[[0.20107314 0.20571849 0.19305588 0.20196906 0.19818346]
[0.19956116 0.206497   0.19219774 0.2022371  0.19950701]
[0.19852805 0.20093426 0.19843033 0.19923802 0.20286934]
[0.19982982 0.2025421  0.19619405 0.2011461  0.20028795]
[0.19893743 0.20526461 0.19141008 0.20293026 0.20145765]], shape=(5, 5), dtype=float32)
original attention score head0 ---------------------
[[0.20107314 0.20571849 0.19305588 0.20196906 0.19818346]
[0.19956116 0.206497   0.19219774 0.2022371  0.19950701]
[0.19852804 0.20093425 0.19843031 0.199238   0.20286933]
[0.19982982 0.2025421  0.19619405 0.2011461  0.20028795]
[0.19893743 0.20526461 0.19141008 0.20293026 0.20145765]]

calculated attention score head1---------------------
tf.Tensor(
[[0.20234193 0.19659588 0.20314567 0.19938873 0.19852772]
[0.20439059 0.19854018 0.19828098 0.19882216 0.19996613]
[0.1981504  0.1989781  0.20315565 0.20173123 0.1979846 ]
[0.2019667  0.19963577 0.19904017 0.19913687 0.20022044]
[0.20230423 0.200125   0.19915625 0.19755708 0.2008574 ]], shape=(5, 5), dtype=float32)
original attention score head1 ---------------------
[[0.20234194 0.19659589 0.20314568 0.19938874 0.19852774]
[0.20439057 0.19854018 0.19828096 0.19882214 0.19996612]
[0.1981504  0.1989781  0.20315565 0.20173123 0.19798459]
[0.2019667  0.19963577 0.19904017 0.19913687 0.20022044]
[0.20230423 0.200125   0.19915625 0.19755708 0.2008574 ]]

calculated attention score head2---------------------
tf.Tensor(
[[0.20181927 0.19517542 0.20552881 0.20081246 0.19666404]
[0.20416309 0.19777557 0.2002391  0.20127144 0.19655083]
[0.19733332 0.19420035 0.20823859 0.20359878 0.19662902]
[0.20185941 0.19888419 0.2001838  0.20064123 0.19843134]
[0.20559046 0.19726498 0.20071685 0.2004946  0.19593315]], shape=(5, 5), dtype=float32)
original attention score head2 ---------------------
[[0.20181927 0.19517542 0.20552881 0.20081246 0.19666404]
[0.20416309 0.19777557 0.2002391  0.20127144 0.19655083]
[0.19733332 0.19420035 0.20823859 0.20359878 0.19662902]
[0.20185941 0.19888419 0.2001838  0.20064123 0.19843134]
[0.20559046 0.19726498 0.20071685 0.2004946  0.19593315]]

calculated attention output ################
tf.Tensor(
[[-0.01935838  0.23451313  0.04786214 -0.3121213   0.18013413  0.25537926
   0.17586923]
[-0.02007196  0.23417734  0.0485854  -0.31237102  0.18114641  0.2551632
   0.17636569]
[-0.0195642   0.2346047   0.04772483 -0.31200075  0.18077154  0.25451547
   0.17425016]
[-0.0206014   0.23423262  0.04830268 -0.31204015  0.18218099  0.255106
   0.17550145]
[-0.01992496  0.23400594  0.04858264 -0.31262934  0.18083805  0.2547874
   0.17601012]], shape=(5, 7), dtype=float32)
original attention output ################
[[[-0.01935837  0.23451312  0.04786216 -0.31212133  0.18013415
    0.25537926  0.17586923]
  [-0.02007195  0.2341773   0.0485854  -0.312371    0.18114641
    0.2551632   0.1763657 ]
  [-0.0195642   0.23460469  0.04772483 -0.3120007   0.18077153
    0.2545155   0.17425014]
  [-0.02060139  0.23423262  0.04830268 -0.31204015  0.182181
    0.25510603  0.17550144]
  [-0.019925    0.23400596  0.04858266 -0.31262937  0.18083808
    0.25478742  0.17601013]]]

9. attention scoresの可視化

ここからはAttentionという機構が何をしているのかを理解するために、MultiHeadAttentionの計算過程で求められるattention scoresを可視化します。attention scoresは、query,key,valueを同じにしたself-attentionの場合には、入力データのどの部分を注目すればモデルが教師データに追従できるかを表すものです。

計算過程の確認とは違い、attention scoresはモデルを学習させて求められるものなので、まず入力データを数多く用意します。

入力データの生成

# 総データ数
BATCHES = 1000

# データは、(SEQS,CHANNELS)形式とする。
SEQS = 5
CHANNELS = 7

# 入力データはランダムに生成する。
train_x = np.random.rand(BATCHES,SEQS,CHANNELS)
print(f"train_x{train_x.shape}")

出力例

train_x(1000, 5, 7)

データ数を1000としています。データの形状は(5,7)と先ほどと変わりません。そして先ほどと同じように入力データはランダムに作成されます。

次に教師データを作成します。

3種類の教師データの作成

# 教師データを3種類作成する。

# 1つのシーケンスデータはそのデータの合計値ですべての要素が入れ替えられる。
# 同じシーケンスデータから教師データを作成しているので、attention scoresは入力queryと同じ場所のvalueが重要になると期待する。
train_y_0 = np.apply_along_axis(func1d=lambda e:[sum(e) for _ in range(len(e))],arr=train_x,axis=2)
print(f"train_y_0{train_y_0.shape} 同じシーケンス内で演算")

# 2番目のシーケンスデータをすべてに足し合わせる。attention scoresは自分自身と2番目のシーケンスが重要になると期待する。
train_y_1 = train_x*1.0 + train_x[:,[1],:]
print(f"train_y_1{train_y_1.shape} 2番目のシーケンスが全体に足される")

# 2番目のシーケンスデータだけになる。attention scoresは2番目のシーケンスが重要になると期待する。
train_y_2 = train_x*0.0 + train_x[:,[1],:]
print(f"train_y_2{train_y_2.shape} 2番目のシーケンスデータにすべてが入れ替えられる")

次の3種類を用意します。入力データは5個のデータが並んでいて、その並びをシーケンスと呼んでいます。また5個のデータのそれぞれ1個は7要素でできています。

1つのシーケンスから答えを導けるデータ
- 例えば1番目のデータから1番目の正解を計算できる。1番目の正解に、1番目以外のデータは使用しない。
- 具体的には7要素の合計値する。
- attention scoresでは、自分のシーケンスのみに影響を受ける、という結果を期待します。
2番目のシーケンスデータを他のシーケンスデータに加える
- 例えば1番目のデータは1番目のデータ＋2番目のデータ、2番目のデータは2倍される、3番目は3番目のデータ＋2番目のデータとなります。
- attention scoresでは、自分のシーケンスと2番目のシーケンスから影響を受ける、という結果を期待します。
2番目のシーケンスデータで他のシーケンスデータを入れ替える
- 1番目、2番目、3番目のデータのすべてが2番目のデータになります。
- attention scoresでは、2番目のデータのみに影響を受ける、という結果を期待します。

これらの3種類の教師データを学ぶモデルを3つ作成します。

モデルの生成

def build_model(num_heads,key_dim,input_shape,type):
  # モデルを作り直す。
  inputs = layers.Input(shape=input_shape)
  x = inputs
  if type=="extended":
    x, att_scores = MultiHeadAttention_biasExpand(num_heads,key_dim)(x,x,return_attention_scores=True)
  else:
    x, att_scores = layers.MultiHeadAttention(num_heads,key_dim)(x,x,return_attention_scores=True)
  return keras.models.Model(inputs=inputs,outputs=x)


models = [
    {"name":"同じシーケンス",
     "train_x":train_x,
     "train_y":train_y_0,
     "model":build_model(num_heads=8,key_dim=CHANNELS,input_shape=train_x.shape[1:],type="extended"),
     },
    {"name":"シーケンス2を加える",
     "train_x":train_x,
     "train_y":train_y_1,
     "model":build_model(num_heads=8,key_dim=CHANNELS,input_shape=train_x.shape[1:],type="extended"),
     },
    {"name":"シーケンス2に入れ替える",
     "train_x":train_x,
     "train_y":train_y_2,
     "model":build_model(num_heads=8,key_dim=CHANNELS,input_shape=train_x.shape[1:],type="extended"),
     },
]

出力例

train_y_0(1000, 5, 7) 同じシーケンス内で演算
train_y_1(1000, 5, 7) 2番目のシーケンスが全体に足される
train_y_2(1000, 5, 7) 2番目のシーケンスデータにすべてが入れ替えられる

モデルはkerasオリジナルのMultiHeadAttentionではなく、後述するバイアス部分を拡張したカスタムレイヤーを使用します。

ヘッド数は8、key_dimは入力データの要素数である7と同じにしています。

モデルの学習

# モデルの学習
for params in models:
  # モデルのコンパイル
  params["model"].compile(optimizer="adam",loss="mse")
  history = params["model"].fit(params["train_x"],params["train_y"],epochs=200,verbose=0)
  print(f"last loss({params['name']}): {history.history['loss'][-1]}")

  # 計算過程の描画
  fig,ax = plt.subplots()
  ax.plot(history.history["loss"])
  ax.set_title(params["name"])
  ax.set_xlabel("epochs")
  ax.set_ylabel("loss (mse)")
  plt.show()

出力例(グラフは省略します)

last loss(同じシーケンス): 0.009346767328679562
last loss(シーケンス2を加える): 0.0012063049944117665
last loss(シーケンス2に入れ替える): 2.331496034457814e-06

入力データは0以上1未満なので最初の平均二乗誤差(mse)約0.01は少し大きい気もしますが、まあある程度学習できています。

学習したモデルに入力データを再度与えて、attention scoresを求めて描画します。

attention scoresの描画

for params in models:
  # attention scores可視化のためにMultiHeadAttentionの出力をモデルの出力とするモデルを作成する。
  eval_model = keras.models.Model(inputs=params["model"].input,outputs=params["model"].layers[-1].output)
  # MultiHeadAttentionの出力を得る。
  att_output, att_scores = eval_model.predict(params["train_x"])
  print(f"train_x:{train_x.shape}")
  print(f"output:{att_output.shape}")
  print(f"att scores:{att_scores.shape}")

  # プロット用のattention scoreは、すべてのヘッドに渡って値を0-1の間に正規化する。
  # これによりどのヘッドが効果を上げているかを見ることができる。
  plot_att_scores = np.apply_along_axis(func1d=sum,arr=att_scores,axis=0)
  mx,mi = max(plot_att_scores.flatten()),min(plot_att_scores.flatten())
  plot_att_scores = (plot_att_scores - mi) / (mx - mi)

  # ヘッド数をattention scoresから取得する。
  nheads = att_scores.shape[1]

  # グラフの列数を計算する。最大を8列とする。
  ncols = 8

  # 描画領域を作成する。
  fig,axs = plt.subplots(nrows=math.ceil(nheads/ncols),ncols=ncols,squeeze=False,figsize=(12,3),facecolor="white")
  fig.suptitle(params["name"])
  fig.subplots_adjust(wspace=0.6,hspace=0.6)
  # 各ヘッドごとに描画する。
  for head in range(nheads):
    ax = axs[head//ncols,head%ncols]
    ax.imshow(plot_att_scores[head],vmax=1,vmin=0)
    ax.set_xticks([i for i in range(plot_att_scores[head].shape[0])])
    ax.set_yticks([i for i in range(plot_att_scores[head].shape[1])])
    ax.xaxis.set_label_position("top")
    ax.xaxis.set_ticks_position("top")
    ax.set_title(f"head {head}")
    ax.set_xlabel("出力")
    ax.set_ylabel("入力")

  # 描画していない領域のクリア
  for col in range(head%ncols+1,ncols):
    axs[-1,col].axis("off")
  plt.show()
  print()

出力例

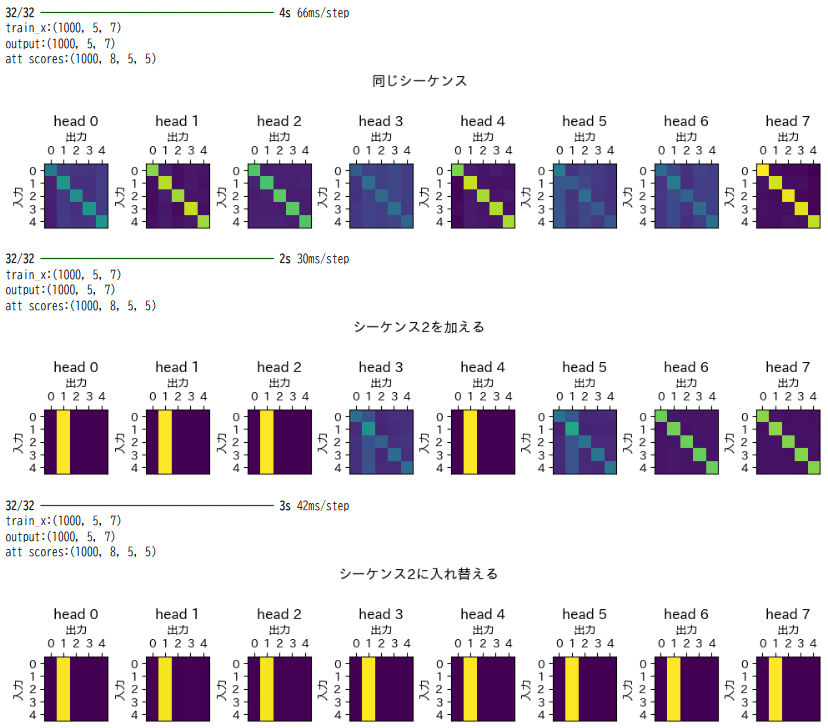
attention scoresは入力データ1つに対して1つが計算されます。ここで図示したattention scoresは入力データの1000個から求められた1000個のattention scoresの平均です。ヘッド数を8としたので、1つのモデルから8つのattention scoresが求められています。図は、明るい色ほど数値が大きく重要な個所を表していることになります。

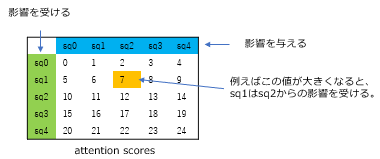
attention scoresの見方です。行、列は入力データのシーケンス数でできています。今回の場合は5です。緑色になっている行が入力です。行列のオレンジでハイライトされた7という個所の値が他の要素よりも大きい場合、[sq0,sq1,...,sq4]と入力があるときにsq1はsq2の値を使って変換される、とみることができます。

これを踏まえて先ほどのattention scoresの結果をみると、同じシーケンスで回答を得ることができる教師データの場合、斜めのラインを見て取ることができます。斜めのラインとは、入力のシーケンスに対して影響を与えるシーケンスは自分自身のみということです。同じシーケンスだけで回答を得られるデータの特徴をよく表しています。

次にシーケンス2を加える教師データの場合、斜めのラインと左から2番目の列の縦ラインが見て取れます。シーケンス2が他のどのシーケンスに対しても影響を与え、かつ、自分自身のデータも回答を得るのに必要である、ということが明らかとなっています。

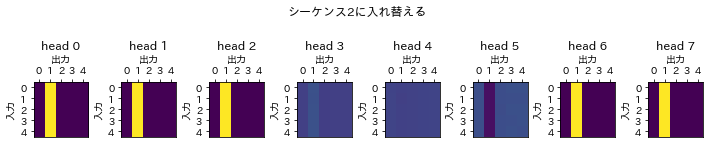
最後にシーケンス2で入れ替える教師データの場合です。斜めのラインが消えて、縦ラインのみが残っています。

このように、教師データを再現するために入力データをどのように変換すればよいのかをMultiHeadAttentionは学ぶことができたとみることができます。

10. カスタムレイヤーによるMultiHeadAttentionのkeyのバイアス拡張について

attention scoresの可視化では、kerasのカスタムレイヤーを用いて独自のMultiHeadAttentionレイヤーを作成して使用していました。その理由は、↓のような縦ラインのattention scoresを作りにくいからです。

その理由を説明するために、まずは入力データに重みの行列を右からかけていることから説明を開始していきます。

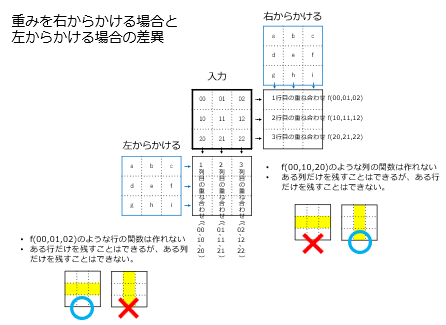
そもそも行列の積は、入力の右から重みをかけると結果は元の入力の行が形を変えるように見れます。例えば計算結果の1行目は入力の1行目を引数とした関数のようなものです。同じ関数が2行目に適用されて計算結果の2行目が得られます。ここでいう関数は線形写像なので例えば1行目と2行目を0にして3行目のみを残すといった非線形な写像はできません。よって右から重みをかけると生成される行列は、ある列のみを残すようなことはできるのですが、ある行だけを常に残すようなことはできません。またちなみに重みを左からかけると逆に行を抽出することは出来ても列を抽出することは出来ません。

ここでattention scoresの計算方法を行列の形式で示します。

右下の赤枠がattention scoresです。この黄色の要素値が他の要素よりも十分に大きい場合、attention scoresに①のような縦のラインが形成されることになります。その場合、そのもとになる1つ上の(4,3)の行列でも②のような縦ラインが形成される必要があります。その行列は転置されたものなので、さらにその上のkeyとw_keyを掛け合わせた行列では③のような横ラインが強調されます。

ここで先の重みを右からかけると入力のある行だけを抜き出すようなことはできない、という事実と合わせて考えるとkeyに右からw_keyをかけている計算では上図のような黄色いラインを作ることができない、ということが分かります。もちろん入力のkeyの値によってはラインができているように見えることもありますが、どのような入力データであっても常に上図のようなラインを形成するようなことはできません。

そこでb_keyと名付けられているkeyに対するバイアスに注目します。kerasでは(1,4)の形状でこれはブロードキャストと呼ばれる(4,4)の形状に引き伸ばされてその上の行列に足し合わされます。ただ引き伸ばされても同じデータが4行になるため相変わらず行ごとの差異は生まれません。そこでこのバイアスを(4,4)の形式で与えます。そのように拡張すると、行ごとの特徴をとらえてある行だけを残すようなバイアスをも作ることができるようになります。

keyのバイアスを拡張した独自のMultiHeadAttentionを以下に示します。

keyのバイアスを拡張したMultiHeadAttentionレイヤー

# カスタムレイヤーの実装
# https://www.tensorflow.org/tutorials/customization/custom_layers?hl=ja
class MultiHeadAttention_biasExpand(tf.keras.layers.Layer):
  def __init__(self,num_heads,key_dim,**kwargs):
    super().__init__()
    self.num_heads = num_heads
    self.key_dim = key_dim

  def build(self, input_shape):
    # kernelの重み
    self.w_query = self.add_weight("w_query",shape=[input_shape[-1],self.num_heads,self.key_dim])
    self.b_query = self.add_weight("b_query",shape=[self.num_heads, self.key_dim])
    self.w_value = self.add_weight("w_value",shape=[input_shape[-1],self.num_heads,self.key_dim])
    self.b_value = self.add_weight("b_value",shape=[self.num_heads, self.key_dim])
    self.w_output = self.add_weight("w_output",shape=[self.num_heads,self.key_dim,input_shape[-1]])
    self.b_output = self.add_weight("b_output",shape=[input_shape[-1]])
    self.w_key = self.add_weight("w_key",shape=[input_shape[-1],self.num_heads,self.key_dim])

    # bias: keyの重みはシーケンス数だけ拡張している。
    self.b_key = self.add_weight("b_key",shape=[self.num_heads, input_shape[-2], self.key_dim])

  def call(self, query, value, **kwargs):
    key = value
    att_scores = []
    for head in range(self.num_heads):
      qw = query @ self.w_query[:,head,:] + self.b_query[head,:]
      kw = key @ self.w_key[:,head,:] + self.b_key[head,:]
      kw_t = qw @ tf.transpose(kw,perm=[0,2,1]) / math.sqrt(self.key_dim)
      att_scores.append(tf.expand_dims(tf.nn.softmax(kw_t),1))
    att_scores = tf.concat(att_scores,1)
    
    att_outputs = []
    for head in range(self.num_heads):
      vw = value @ self.w_value[:,head,:] + self.b_value[head,:]
      av = att_scores[:,head] @ vw
      att_outputs.append(av @ self.w_output[head] + self.b_output)
    return (sum(att_outputs),att_scores)

# 増やしたバイアスの形状を確認する。
# seqs=4, channels=5
inputs = layers.Input(shape=(4,5))
layer = MultiHeadAttention_biasExpand(num_heads=2,key_dim=3)
layer(inputs,inputs)
for w in layer.weights:
  print(f" {w.name}, shape={w.shape}")

出力例

multi_head_attention_bias_expand/w_query:0, shape=(5, 2, 3)
multi_head_attention_bias_expand/b_query:0, shape=(2, 3)
multi_head_attention_bias_expand/w_value:0, shape=(5, 2, 3)
multi_head_attention_bias_expand/b_value:0, shape=(2, 3)
multi_head_attention_bias_expand/w_output:0, shape=(2, 3, 5)
multi_head_attention_bias_expand/b_output:0, shape=(5,)
multi_head_attention_bias_expand/w_key:0, shape=(5, 2, 3)
multi_head_attention_bias_expand/b_key:0, shape=(2, 4, 3)

計算の過程は先に示した手動でMultiHeadAttentionの計算を行うものと同じです。kerasライブラリとの違いは、b_keyの部分です。ヘッド数2, key_dim 3の場合には、kerasではshape=(2,3)となるところこの独自のMultiHeadAttentionではshape=(2,4,3)となります。あいだの4は、入力データのシーケンス数です。

ここからは拡張したMultiHeadAttentionの効果を示すために、拡張していないオリジナルのkerasのMultiHeadAttentionレイヤーを使って実行した例を示します。

モデルの生成の拡張

models = [
    {"name":"同じシーケンス(但しkeyのバイアスが拡張されていないkerasオリジナル)",
     "train_x":train_x,
     "train_y":train_y_0,
     "model":build_model(num_heads=8,key_dim=CHANNELS,input_shape=train_x.shape[1:],type="keras"),
     },
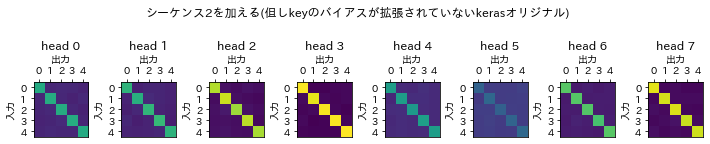
    {"name":"シーケンス2を加える(但しkeyのバイアスが拡張されていないkerasオリジナル)",
     "train_x":train_x,
     "train_y":train_y_1,
     "model":build_model(num_heads=8,key_dim=CHANNELS,input_shape=train_x.shape[1:],type="keras"),
     },
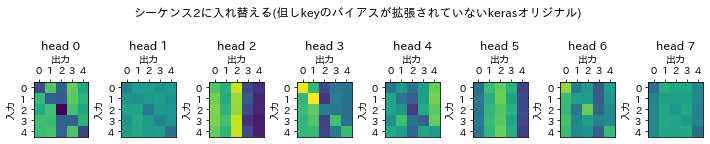
    {"name":"シーケンス2に入れ替える(但しkeyのバイアスが拡張されていないkerasオリジナル)",
     "train_x":train_x,
     "train_y":train_y_2,
     "model":build_model(num_heads=8,key_dim=CHANNELS,input_shape=train_x.shape[1:],type="keras"),
     },
]

まず、3つの教師データに対するkerasライブラリのモデルを作成します。上で既に示した「モデルの生成」のmodels変数を入れ替えます。

先の「モデルの学習」を実行すると以下のような結果が出力されます。

last loss(同じシーケンス(但しkeyのバイアスが拡張されていないkerasオリジナル)): 0.011491662822663784
last loss(シーケンス2を加える(但しkeyのバイアスが拡張されていないkerasオリジナル)): 0.06803781539201736
last loss(シーケンス2に入れ替える(但しkeyのバイアスが拡張されていないkerasオリジナル)): 0.06206922605633736

シーケンス間の影響を与えた下2つの平均二乗誤差(mse)が独自のMultiHeadAttentionレイヤーに比べて明らかに大きくなっています。

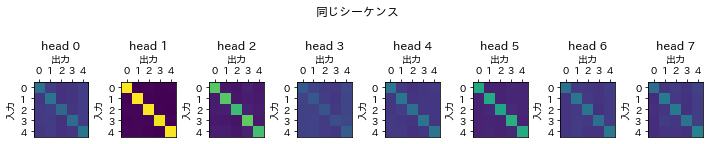
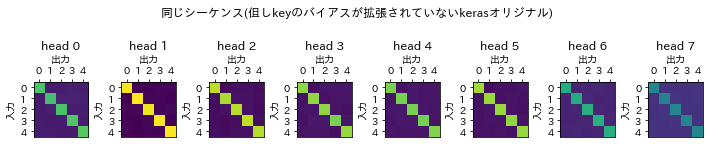
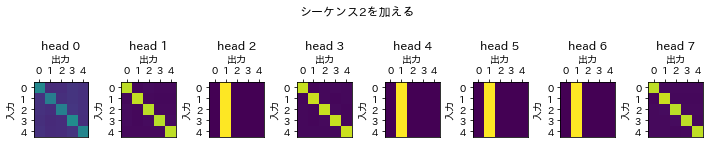
次に図示したattention scoresを確認していきます。図は上に先にすでに示したバイアスが拡張されたもの、下にkerasライブラリのものを示しています。

同じシーケンスのデータだけを使用する場合には、kerasのMultiHeadAttentionでもあまり違いはありません。

シーケンス2を加えるデータの場合、attention scoresから縦のラインが消えています。

シーケンス2に入れ替える場合、バイアスを拡張した独自のものでは縦ラインだけで構成されていてkerasのでは縦ラインが形成できにくいため、attention scoreは入力データの特徴をとらえきれていません。

以上のように今回のデータではattention scoresに縦ラインを作ることはオリジナルのkerasライブラリではできませんでした。ただデータによっては縦ラインを作り出すこともあります。

11. ヘッド数について

attention scoresの可視化の例では8つのヘッドを用いました。ここではあえてヘッド数を1にして実行し、その結果を考察します。

まずバイアスを拡張したモデルとkerasライブラリを比較したときと同様に、「モデルの生成」のmodels変数を入れ替えます。

モデルの生成の拡張

models = [
    {"name":"シーケンス2を加える(但しnum_headsが1の場合)",
     "train_x":train_x,
     "train_y":train_y_1,
     "model":build_model(num_heads=1,key_dim=CHANNELS,input_shape=train_x.shape[1:],type="extended"),
     },
]

「モデルの学習」を実行すると次のような結果が得られます。

last loss(シーケンス2を加える(但しnum_headsが1の場合)): 0.020943202078342438

ヘッド数が8のモデルの損失が約0.0012だったのに比べて200回の学習時点での損失は増えています。

そしてattention scoresを描画すると上図のようになります。1つのヘッドで斜めと縦のラインが学習されつつあります。これは畳み込みニューラルネットワークのフィルターと違い、複数の特徴を1つのヘッドで学習できることを示唆しています。よってここから考えられるMultiHeadAttentionのヘッド数の設計指針は、計算コストが許すならヘッドを多めにする、ただし精度はヘッドを多くしてもあまり変わらないかもしれない、です。

ただ入力データの特徴空間に損失のローカルミニマムがある場合、ヘッド数を増やすことによりいくつかのヘッドがローカルミニマムに陥ってもどれか1つは真の値に近づける、ということも考えられます。

まとめるとヘッド数は、ローカルミニマムがあるような特徴空間ならばヘッド数を増やして真の解を得るためのロバスト性を上げることができる。しかし1つのヘッドが真の解を得たら他のヘッドは恐らく不要なのでたくさんあれば精度が向上していくというわけではない。

12. key_dimについて

MultiHeadAttenionの内部状態の状態数であるkey_dimを1にして実行してみます。

まず「モデルの生成」のmodels変数を以下のように入れ替えます。

モデルの生成の拡張

models = [
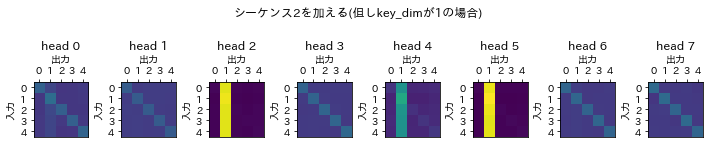
    {"name":"シーケンス2を加える(但しkey_dimが1の場合)",
     "train_x":train_x,
     "train_y":train_y_1,
     "model":build_model(num_heads=8,key_dim=1,input_shape=train_x.shape[1:],type="extended"),
     },
]

「モデルの学習」を行うと次のような結果が得られます。

last loss(シーケンス2を加える(但しkey_dimが1の場合)): 0.07653312385082245

key_dimが8のときには約0.0012だった損失は、増えています。

attention scoresの可視化を行うと、斜めのラインがしっかりと出ていないことが伺えます。このデータはシーケンスの自分自身と2番目のシーケンスから影響を受けるという2つの特徴があり、そのうち1つしか学習していないとも見れます。

これらのことからkey_dimは基本的には大きいほうが良い、ただし従来の様々なニューラルネットワークと同様にパラメータ数が多くなると学習コストが上がるだけでなく過学習のリスクもあることはこのkey_dimの値についても同じです。

参考

公式のtf.keras.layers.MultiHeadAttention API
MultiHeadAttentionの論文

PyTorchでMultiHeadAttentionを検算しているサイト

kerasのMultiHeadAttentionについて質問しているサイト
 kerasのMultiHeadAttentionについて質問しているサイトが引用しているサイト