誰でもわかる！レスポンシブ時代の画像処理入門

（iPhone女子メンターがタイトル画像つくってる流れにあやかってみました笑）

1. Introduction

みなさん、こんにちは。iPhoneメンターのとうようです。
この記事は Life is Tech ! Advent Calendar 2018の21日目の記事です。誕生日の１ヶ月後という理由だけでこの日を取ってみました笑

昨日はえんぽーのインサイト発想に関する記事でしたね。えんぽーの言うように僕が「歩く技術力」ならえんぽーは「歩くUXプロフェッショナル」だなぁと思いながら、深夜に読んでてすごくためになりました😊（※深夜に急いで付け足したのですごい適当なこと言ってます笑でもいい記事だったのは本当だよ）

さて、Qiitaに記事を書くのも久しぶりだなぁという感じになってしまったのですが、今回は僕も卒論シーズンということで今取り組んでる研究で扱っている画像処理の技術について紹介していこうかなと思います。そちらの実装をReact+MobX+TypeScriptでやっているので、iPhoneメンターながら載せるコードもTypeScriptになってしまうのですがご容赦ください。といっても今回はかなり要の部分をしっかりまとめるつもりなので、この記事を理解してもらった暁にはiPhoneなみなさんもSwiftで同じようなコードが書けるようになっていると思います（多分）
ちなみに今週の頭には同じくiPhoneメンターのちゃーりーが画像処理の記事を書いていましたね。ちゃーりーの記事がOpenCVでのアプリケーション例のようなものだったのに対し、こちらはもう少しアルゴリズムチックな話題になります。やってることもかなり違うのでぜひ両方読んでみながら画像処理という分野の幅広さを体感するのもいいんじゃないかなと思います。

そんなわけで今回紹介するのはSeam Carvingという技術です。Seam Carving¹自体は2007年に発表された技術で、画像を「いい感じ」にサイズを変えてくれるという技術です。例えば以下は原著論文に載っている例ですが、このように元の画像を入力としてあたえると画像の内容がなるべく崩れないようにサイズを変えてくれるという技術になっています。（この場合はどちらも入力として幅の狭い画像が与えられてそのとなりの幅の広い画像が出力される例になってます。）

この技術の特にすごい部分は今では機械学習をつかってやりそうなこのような処理を、動的計画法というとても基本的なアルゴリズムを用いて実現しているところです。
そんなSeam Carvingそれ自体は（実際スマホの誕生に触発されて生まれたようなものなのですが）たくさんの解説記事が出ておりめずらしいものではありません。実はPhotoshopにも実装されてたりします。また11年もたっているので多くの発展例や同じようなことを動画に適用する研究などもなされています。

そういう基本的な実装などについては先人たちの記事に任せるとして、今回の僕の記事ではあまり一般の方には広まっていない原著論文のAppendixにかかれている内容と、それを高速化した論文²の内容について、画像処理初心者でもわかりやすいように基本から解説していこうと思います。（実際僕自身が画像処理の基本の解説が少なすぎて理解するまで時間がかかったので...）
もちろんそこらへんは知っているよという人は飛ばして3章から読んでみてください。

論文の紹介ということで堅苦しいイメージになってしまいそうですが、がんばってわかりやすく書こうと思うのでよろしくおねがいします。

2. Basics

2-1. Basics of Image Processing

まずは、基本の基本となる画像処理についてざっくり必要な部分を紹介していきたいと思います。

コンピュータ上での画像は大きくわけると２つの種類にわかれます。それはベクター形式とビットマップ形式です。すごく大雑把に言えばイラレとフォトショの違いです。
このうち画像処理で扱われるのは主にビットマップ形式のほうになります。

ビットマップ形式は拡張子で言えばpngやjpgなどがそれにあたりますが、これらはピクセルという単位を基本単位としています。この１ピクセルにひとつの色が割り当てられており、これを寄せ集めることでちょうどモザイク画と同じ原理でキレイな画像に見えるわけです。

このため写真ではよく4000x3000のようにサイズを表しますが（これが縦横に詰まってるピクセルの数でサイズをあらわしているわけです）、このサイズに使われている数字が大きくなればなるほど高画質な画像と言われ、よりキレイな画像になります。

画像処理においてはこのピクセルの色を足したり引いたり掛けたり割ったりして変えていくことで、１ピクセルに対する処理としては単純なことをしていても、寄せ集めてみるとなんかすごいことになってる、というようなことを実現していきます。
この計算時に扱う数値は基本的にはどのプログラミング言語でもRGBAという４つの数字で表されます。略さずにいうとこれはRed(赤)、Green(緑)、Blue(青)、Alpha(透明度)の４つであり、それぞれを（仕様によって異なる場合もありますが）基本は0〜255の256段階で調節し様々な色を作ります（ちなみに256という数字は2の8乗であり各色の情報が8bitで表されるところから来ています。興味のある方はぜひここらへんのことも調べてみてください。）

すごく簡単な例でいうと、例えばグレイスケールの画像はこのRGBの平均をとったりある定数をかけて３つの値を近いものにすることで灰色にしています。どのように計算するかで変わってくる部分もありますが、赤・緑・青の値が近ければ近いほど色の見え方としては白黒に近づくので「平均をとる」というごく簡単な演算で実現できるわけです。

このようにRGBの値をいじることでグレースケール以外にも色を変えるような画像フィルターは比較的簡単に実現できることはなんとなくわかるかなと思います。ではSeam Carvingのように画像の内容に応じてどうこうする、といった処理はどのように実現するのでしょうか？
この課題にあたったとき、次節で紹介するエネルギーという概念が関わってきます。

2-2. Basics of Energy Function

次に、Seam Carvingでも肝となるエネルギーという概念について紹介していきたいと思います。
エネルギーとは簡単に言えば**「その画像の各ピクセルがどのぐらい◯◯の処理において重要か？」**ということを表す数値です。◯◯と書いたとおりこれは一種類ではないのですが、例えばSeam Carvingでは次のような計算式で出るエネルギーを使います。

e=\left|\frac{\partial I}{\partial x}\right| + \left|\frac{\partial I}{\partial y}\right|

偏微分が出てきましたね。微分を知らない人はもちろんなのですが、たとえ知っていたとしてもこの数式を出されて戸惑う人も多いのではないでしょうか？
微分は本来連続的なものにかけるものですが、プログラミングにおいて画像はピクセルという離散的な値を扱うことになるので単純には適用できないわけです。また二次元かつ密につながっているので隣接しているピクセルが一つあたり8個も存在しておりこれをどう扱うかという問題もでてきます。

ここにはさまざまなやり方があったりするのですが、その中でも様々な実現方法のベースとなるフィルターとしてConvolutionフィルターというものがあります。今回はこのConvolutionフィルターを軸に、Seam Carvingの実装としてよく採用されてるSobelフィルターについて紹介したいと思います。

まずConvolutionフィルターとはそもそもなにかというと日本語で畳み込みと訳されるそのままの意味で、「あるルールに従って１つのピクセルに値を畳み込むような処理」のことを言います。
言葉だけだとわかりにくいので図で見てみましょう。まず登場人物は次の２つです。

（余談ですがXd³のRepeat Grid便利ですね。多分こういう解説では最強な気がします笑）

そしてこの左の行列を使って各ピクセルに対して演算をかけていきます。
この演算はすごく単純で、各ピクセルが左の行列の中心になるように行列を重ね、行列が重なっているピクセルの値に対応する要素の数字を掛けて最後すべて足せば終わりです。次の図にこのことを図解してみましたが、このように中心に行列を畳むように足していくのでたしかに畳み込みという言葉のニュアンス通りだなぁと思えてくると思います（本当の由来は調べてないので注意してください。ただあながち間違っていないと思います。）

これがConvolutionフィルターでした。ちなみに行列がはみ出す端っこのピクセルを考える際にもいくつか方法がありますが一旦詳細は割愛したいと思います。主な例としては端のピクセルを複製したり0として計算したりというものが多いです。

Sobelフィルターはこの行列に以下のような２つの行列を使うものになります。

X=\left(\begin{array}{ccc}-1&0&1\\-2&0&2\\1&0&1\end{array}\right)\\
Y=\left(\begin{array}{ccc}-1&-2&-1\\0&0&0\\1&2&1\end{array}\right)

このような行列でConvolutionフィルターの処理をかけることによってそれぞれ横方向の色の変化量、縦方向の色の変化量を各ピクセルに対して求めることができます。つまり$\left|\frac{\partial I}{\partial x}\right|$や$\left|\frac{\partial I}{\partial y}\right|$が対応してくるわけです。これは順にマイナス・ゼロ・プラスとなっていること、斜め方向への隣接は1で辺を共有してるところは2と大きくなっていることからなんとなくイメージがわくのではないでしょうか。

あとはどうイメージをふくらませて納得感を得られるかの問題なのでぜひ変化量であるということと、ここまで紹介してきた計算方法を照らし合わせながら考えてみてください。
そんなわけでこれを実際に計算してみると色の変化の大きい部分の値が大きくなり、まるでものの輪郭が強調されるかのようなフィルターになってくれます。

（実際にフィルタをかけた画像 http://www.mis.med.akita-u.ac.jp/~kata/image/sobelprew.html より）

Seam Carvingではこの結果を使ってなるべくものの形が崩れないような変形の仕方を見つけていくわけです。詳しくは3-1で紹介するとして、2章の最後として動的計画法について紹介していきます。

2-3. Basics of Dynamic Programming

基礎編の最後として、動的計画法とはなんぞやということも触れておきたいと思います。
動的計画法は競技プログラミングで頻繁に使われるアルゴリズムであり、様々なことに応用することができるテクニックです。

ざっくりまとめると**「直前までの計算結果を使って次の計算をすることを繰り返す」**のが動的計画法です。この性質から簡単な動的計画法は対応する漸化式を書くことが出来ます。
ここではフィボナッチ数列を例にとって見てみましょう。

フィボナッチ数列を知らない人のため軽く紹介しておくと、これは直前２個の和が次の数字になっているという性質をもった数列のことを言います。具体的には次のような数字列です。

1,1,2,3,5,8,13,21,34,...

そしてこれは次のような漸化式で表せます。

F_0 = 1\\
F_1 = 1\\
F_{n+2}=F_{n+1}+F_n

この時点で基本構造がさきほど紹介した動的計画法の概要とほぼ同じことがわかるのではないでしょうか。
実際にコードとして書いてみると以下のようになります。

fibonacci.ts

let fib: number[] = [];
fib[0] = 1;
fib[1] = 1;
for (let i = 2; i < 50; i++) {
  fib[i] = fib[i - 1] + fib[i - 2];
}

こうすることでfib[49]、つまり50番目のフィボナッチ数列の数を求めることが出来ました。

このように数学の数列と非常に似た動的計画法なのですが、この考え方を応用するとさまざまなことが比較的少ない計算回数で求めることができるようになります。
その力を感じるために、基礎編の締めとして動的計画法が使われる代表的な問題でもあるナップザック問題を見てみましょう。

ナップザック問題は次のような問題です。

価値と重さが決まっている複数の品物を容量が一定のナップサックに詰め込むとき、ナップサックに詰め込める品物の価値の和の最大値は何であるか？
（ http://dai1741.github.io/maximum-algo-2012/docs/dynamic-programming/ より）

それではこれを動的計画法で解けるようもう少し形式化したかたちにしてみます。するとこんな問題になります。

今$n$個の価値と重さが決まっている複数の品物があります。品物には番号がついており、$i$番目の品物の価値が$v_i$、重さが$w_i$です。一方ナップザックには重さが$C$になるまでしか品物を詰め込めません。この時ナップザックにつめられる品物の価値の総和の最大値を求めてください。

問題を解くことが今回の目的ではないのでさっそく答えの考え方を紹介していきましょう。
動的計画法を使うということでうまく直前までの答えを使っていくような解き方がわかればよいということになります。今回の場合、求めるのは価値の総和、制限になっているのは重さの総和なのでこの「直前」を重さにからめて考えてあげると良さそうです。

よって次のような配列を作ります。

• $dp[i][j]$: $i$〜$n-1$番目までの商品を使って重さ$j$以下にしたときの価値の総和の最大値

こうすることで次のような漸化式をたてることが出来ます。

dp[n][j] = 0 \\
dp[i][j] = \begin{cases}dp[i+1][j] & (j < w_i)\\\max\left( dp[i+1][j],\  dp[i+1][j-w_{i}] + v_{i}\right) & (j \geq w_i)\end{cases}

$n$番目の品物はない（0から数えてるため）のでその価値はすべて0になります。一方それ以外の場合$n-1$〜$i+1$番目までの結果がすでに決まっていれば、$i$番目までを使ったとき重さ$j$で使える価値の総和の最大値は$i$番目の品物を使わないか、$i$番目の品物を使うかの二択に絞られます。なので下のほうの式のように、重さ$j$が$w_i$より小さいときは品物が使えないので$dp[i+1][j]$、そうでないときは$j-w_i$の重さでつめられる最大価値に$i$の品物をつかって$v_i$を足す場合と使わない場合の大きい方というかたちで決めることが出来ます。

このように漸化式がたつと以下のようにこの問題を解くプログラムが書けます。

knapsack.ts

let dp: number[][] = [];
for (let i = 0; i <= n; i++) {
  for (let j = 0; j <= C; j++) {
    dp[i][j] = 0;
  }
}
for (let i = n - 1; i >= 0; i--) {
  for (let j = 0; j <= C; j++) {
    if (j < w[i]) dp[i][j] = dp[i+1][j];
    else {
      dp[i][j] = Math.max(dp[i+1][j], dp[i+1][j-w[i]] + v[i]);
    }
  }
}

これでdp[0][C]を見てあげれば求めたい答えになっているというわけです。
このようにごく単純に考えると、各品物を入れるか入れないかの二択で繰り返していきすべての場合を調べるという方法で$2^n$回計算しなければいけなそうなところを$nC$回の計算で求めることができました。

これが動的計画法の強みです。

さて、ここまで真面目に読んできてくれた人は、ピクセルのこと、エネルギーのこと、動的計画法のことを大分わかってきたんじゃないでしょうか？この３つさえわかっていればSeam Carvingを理解するまではもうあと一歩です。というわけで次章からその具体的な方法の紹介に入っていきたいと思います。

3. Algorithm

3-1. Seam Carving

それではSeam Carvingが実際どのようなアルゴリズムなのかということについてざっくり見ていきましょう。

そもそもseamという単語は「縫い目」という意味を持ちます。比較的耳にする言葉の中では「シームレス」という単語が一番馴染みがあるのではないのでしょうか。縫い目（seam）を少なくする（less）のでシームレスというわけですね。
Seam Carvingもその字面の通りで、縫い目（seam）を削っていく（carving）ことで画像のサイズを変えていく手法になっていきます。

この写真は英語版Wikipediaから持ってきていますが、この赤い線が削られるseamです。
このseamをどう選ぶか決めるために動的計画法を使い、動的計画法で計算する値としてエネルギーを使います。

具体的な手順を見ていきましょう。
まずは2-2で紹介した手順でエネルギーを計算します。
エネルギーを計算すると変化量の大きいところほど大きい数字が、小さいところほど小さい数字が各ピクセルに割り当てられているかたちになります。この時、なるべく画像の情報を壊さないように削るということはなるべくエネルギーの小さいピクセルから消していくということになります。そのためふくまれるピクセルのエネルギーの総和が一番小さいseamを消していくというのがSeam Carvingの基本戦略になります。

ではどのようにこの「ふくまれるピクセルのエネルギーの総和が一番小さいseam」を探していくのでしょうか？そこで登場するのが動的計画法です。
ここからは少し図を用いて見ていきましょう。

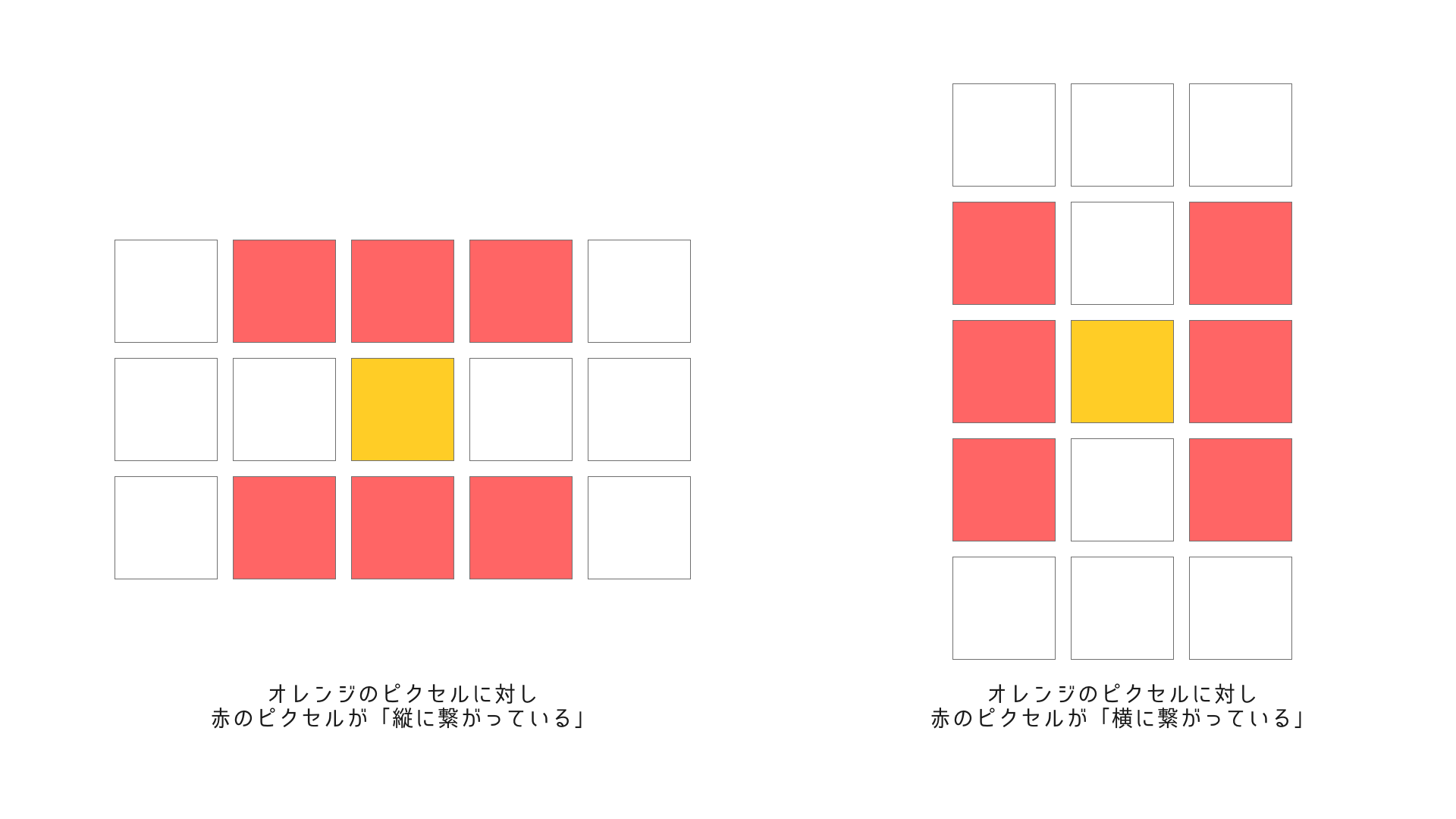
まず大前提としてseamに含まれているピクセルは繋がっていなくてはなりません。この「繋がっている」というのは縦にはしるseamの場合図の左側に表されるように上下に３つずつの合計6ピクセル、横にはしるseamの場合は図の右側のように左右３つずつの合計6ピクセルが繋がったピクセルということになります。

次に行うのは端から順にそのピクセルにたどりつくseamの中で最小のエネルギーになるもののエネルギーを求めていくことです。
この過程が動的計画法でできます。なぜならこの時点ではそこまでのseamがどのように繋がっているかという情報は関係なく、純粋に一個前までの各ピクセルに対するseamのエネルギーの最小値さえ求まっていれば考えてるピクセルにつながるseamのエネルギーの最小値も求められるからです。

よって、今回は縦方向のseamで考えますが、次のような漸化式が成り立ちます。

M[0][x] = energy[y][x] \\
M[y][x] = \min\{M[y-1][x-1], M[y-1][x], M[y-1][x+1]\} + energy[y][x]

なお$x-1$が$0$未満になるなど定義できない場所は正の無限大になっているとします。
この式によってすべてのピクセルに対して**そのピクセルにたどりつくseamのエネルギーの最小値（ただしそのピクセルより下は考えない）**が求まりました。
これを一番端にいくまで繰り返していきます。

消すseamに実際どのピクセルが入っているかを考えるのはここまでくれば簡単です。
まず最終段、つまり縦の場合は$M[height-1]$の部分のエネルギーは実際のseamのエネルギーになっているのでまずこの中から最小のピクセルを探します。

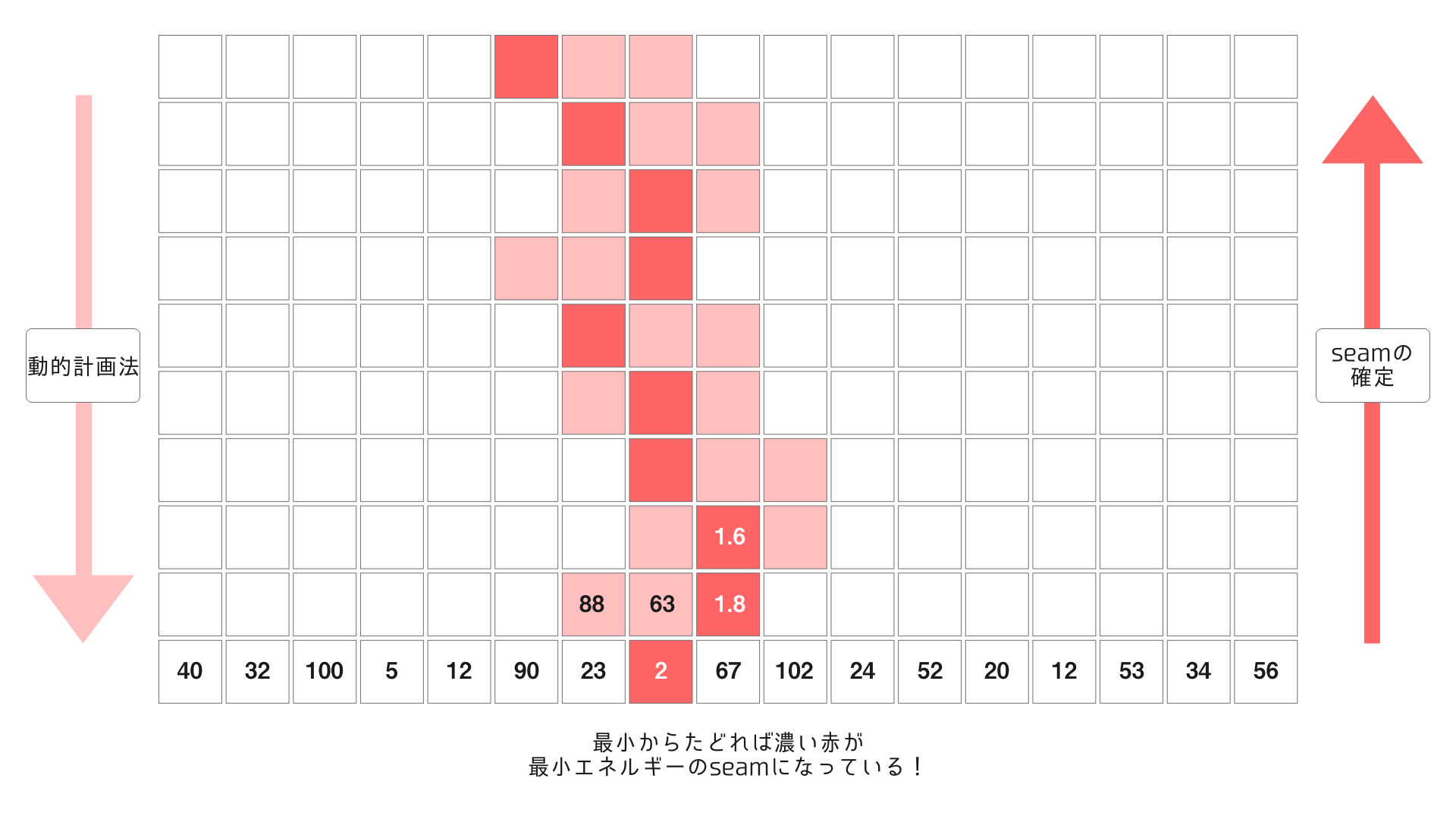
続いて見つかったピクセルから上に繋がっているピクセルの中で$M$の値が最小になっているものをたどっていきます。これを繰り返していけば最小のseamの具体的なかたちがわかります。動的計画法において確定した段はそれ以降触られないので下から計算で選ばれたものをたどっていくというすごく単純な操作でどの値を使っていったのかがわかるのです。

単純なSeam Carvingではここまでできたら、そのseamを消し残った部分でまたエネルギーの計算からやり直していきます。
しかしこの過程は毎ステップ全部のピクセルを調べていかなければならないので、狙ったサイズに変形するという過程ではまだしもインタラクティブにサイズを変えるといった目的ではさすがに計算に時間がかかりすぎます。
それが縦横両方変えなければならない！となると詳しくは解説しませんが⁴どういう順に消すべきなのかも考慮しなきゃいけないのでさらに計算に必要な時間は増していきます。

そこで提案されているのが次の節で紹介するConsistent Index Mapというものです。
これもすごく単純なアイデアで実現されているので、疲れた人はすこしここで休憩しつつ読み進めてみてください。

3-2. Consistent Index Map

さてここまでの内容がSeam Carving自体についてよく知られており、簡単なのでみんなに実装されている部分でした。
続いてこの記事のメインコンテンツである、原著論文のAppendixに書かれたConsistent Index Mapというものの作り方について解説していきたいと思います。

Seam Carvingをインタラクティブに行いたいと思った時、真っ先に思いつくアイデアは「最初に消す順番を決めておいて、それにそって消せばいいじゃない！」というものです。Consistent Index Mapも直訳すればわかるとおりこのアイデアに基づくものです。
一方向のみを考えるのであれば順次消していきながら3-1で紹介したアルゴリズムをあらかじめ実行すればこれは簡単につくれます。

しかしこれには縦横両方を消したい！となった時に問題が起こります。
それぞれの方向で別々に上で言った方法で消す順番を決めてしまうと、そのそれぞれは一方向だけ削っていったときのエネルギーで考えているため悪い結果になりやすい上に、縦のseamと横のseamは交差するときいくつかのピクセルを共有してしまっているので画像がうまくつながらなくなってしまうことがありうるからです。

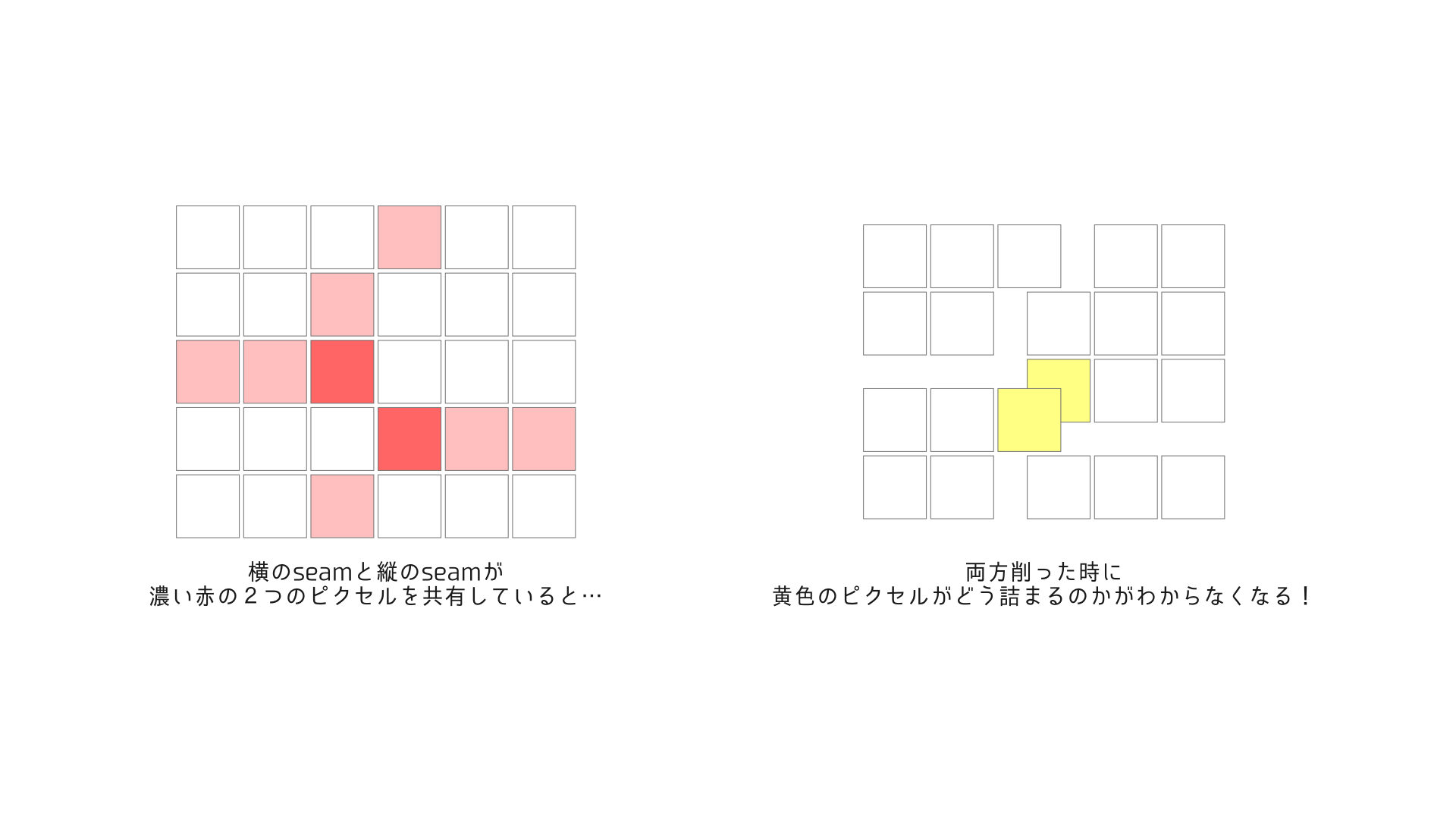
これを解決するためにはひとつseamに対して制約をあたえる必要があります。それはすべてのseamがオリジナルの画像上で繋がっていなければならないというものです。どういうことでしょうか？

通常のSeam Carvingはさきほど説明した通り、seamを計算する際にそれまでに削ったseamを取り除いた画像上で繋がっているものを探していくというアルゴリズムです。このため元の画像上で考えると下の図のように元の画像上では途中で途切れているseamというものが存在してしまいます。

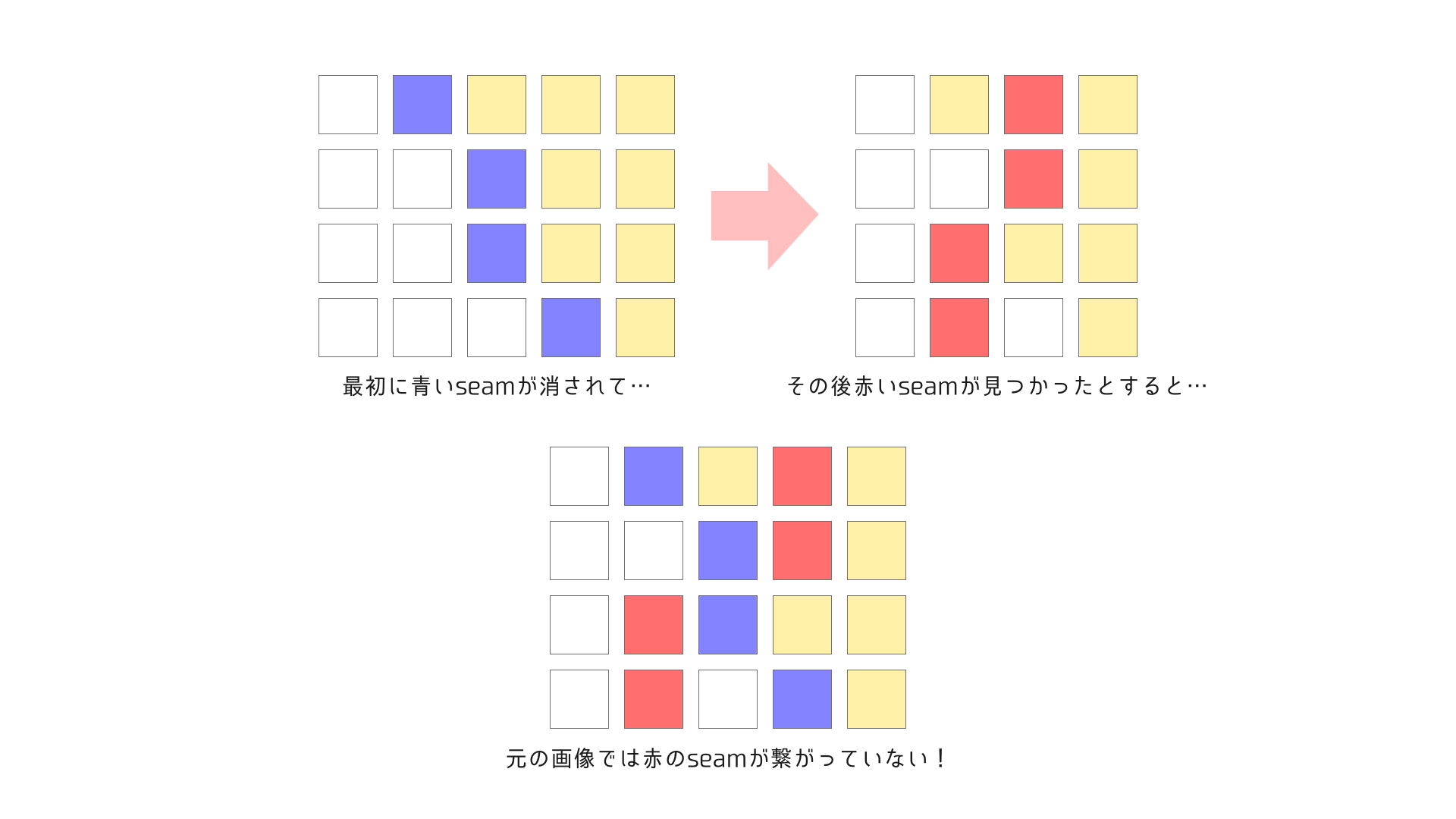
これだと縦と横のseamの交差するパターンがいくつも増えてしまい考えにくいです。そのためこのようなことが無いようにseamを計算していきます。

この求め方はアイデアとしてはかなりシンプルです。
通常のSeam Carvingでは計算する際に各ピクセルごとに考えていました。そのため計算し終わったそこまでのseamを共有する複数のピクセルが存在しえたことになります。

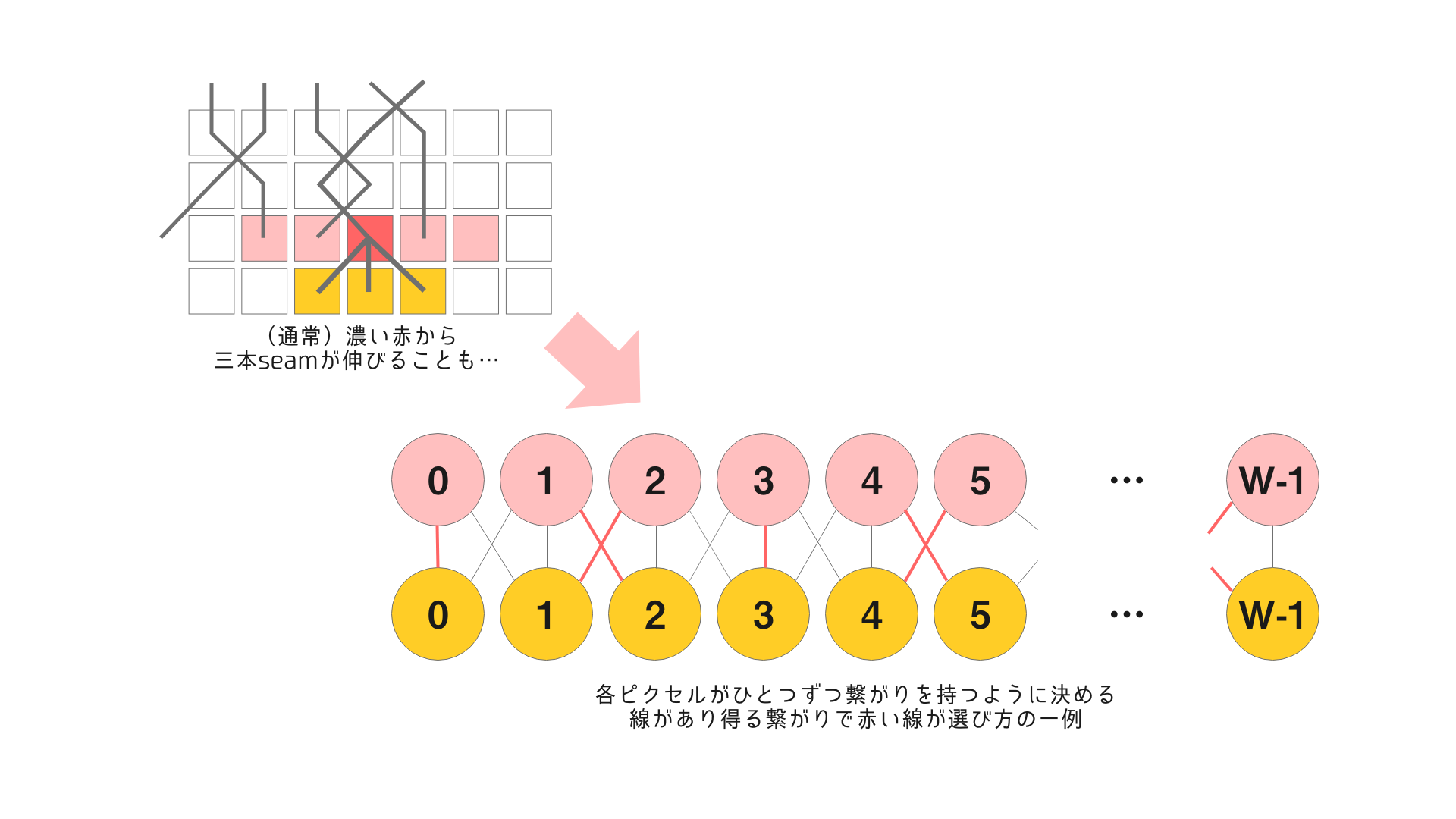
オリジナル画像で繋がったseamを求める際は、このような部分があると困るので、考えている段のピクセルすべてのつながり方を同時に決めてあげます。こうすることで計算し終えるとそれぞれピクセルを共有していないseamが幅や高さ分求まっているわけです。
では、この同時に決めるというのはどうやるのでしょうか？これは全体で最適なseamの組み合わせが求まるように２つの段のつなぎ方を決める、「割当問題」というものになっています。

ここで原著論文ではハンガリアン法というものを使用しています。
その詳細は3-3を紹介してしまうと馬鹿らしくなってしまうので省きますが、これによってオリジナル画像の上で途切れがないseamの一覧が手に入ります。

実際にはこれをまず縦方向で行います。次に横方向も決めるのですが、この時に複数ピクセルを縦と横のseamが共有していたらまずいので割り当てする際に以下のように斜めにすでにつながっているピクセルがあった場合それを避けて横を計算していきます。

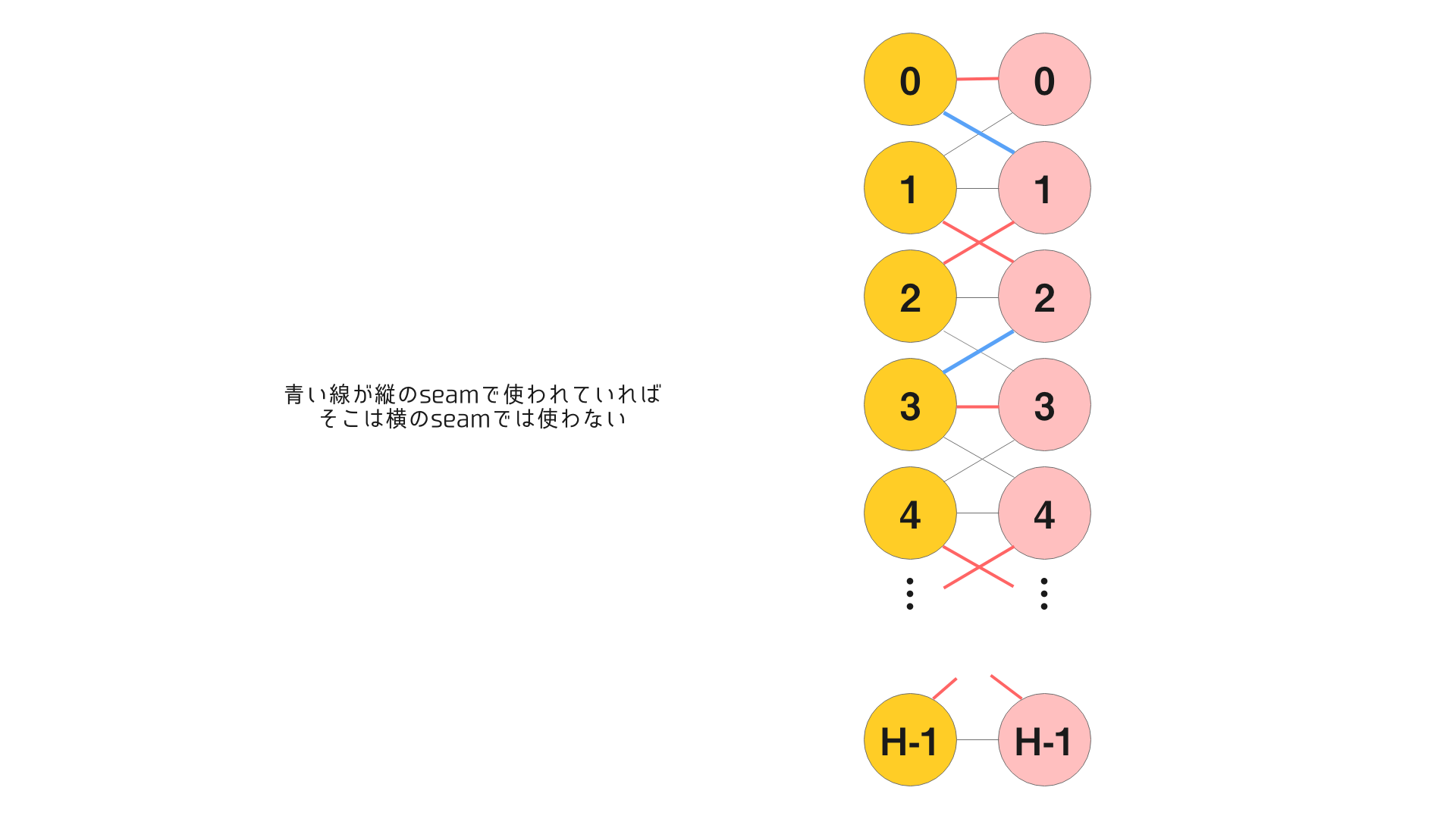
この一手間を加えることで、どっちから消していっても画像が壊れないseamの消す順番表、Consistent Index Mapの縦方向のものと横方向のものを手に入れることが出来ます。

これさえ計算してしまえばいくらでもインタラクティブにSeam Carvingが出来てしまいます（もちろん通常のSeam Carvingより劣ってしまう部分もありますが）
ですがこの過程で用いたハンガリアン法、これがとても重く、nピクセルとnピクセルの割り当てをしようとすると$O(n^3)$⁵の計算をしなければいけないので前計算とはいえすごく時間がかかります。

そこでこの割当部分を高速化しようと提案されたのが最後に紹介するReal-time content-aware image resizingになります。

3-3. Real-time content-aware image resizing

最後に3-2で紹介したものを高速化し、実用的にしてくれた2009年に出ている論文について紹介していきたいと思います。
3-2で問題になっていたのは２つの段の割り当てに必要な計算回数でした。ではこれをどうやって高速化すればよいのでしょうか？

ポイントになるのは割り当ての仕方が各ピクセルに対し三通りしかないという部分です。この制約によって割り当てにわざわざハンガリアン法を用いなくとも割り当てを求めることが可能になります。
そしてここでも出てくるのは動的計画法です。どう考えればよいのでしょうか？

実は今考えている割り当ては先程紹介した制約により端から考えると大きく２パターンに分けられます。上の図に示していますが、ひとつが端っこ同士を繋げた場合、もうひとつが斜めに繋がる場合です。
特に斜めに繋がる時、下の段のw-1番目のピクセルに繋げられるのが上の段のw-1番目もしくはw-2番目しかないため、自ずと上の段のw-2番目の繋がる先がw-1番目のピクセルに決まります。このおかげでこれ以上のパターンはでず、この2パターンのみがありうる繋がり方とわかります。

そして繋がりが確定した部分を無視すると残ったピクセルはw-2個もしくはw-1個の割り当てになります。同じ構造が再び出てきました。そうです、ここでまた動的計画法の登場です。

では具体的にどんな式で求めていけばよいでしょうか？今後のためにいくつかの定義をしておきましょう。
まずは繋がりに対するコストの定義です（本当は重みという言葉のほうが適切かもしれないですが、一旦この記事ではすべてコストと呼ぶことにします。）$i$番目と$j$番目のピクセルが繋がる際のコストを$w(i,j)$と定義します。
これは考えている２つのピクセルのエネルギーを足すというのが一番シンプルな定義の仕方ですが、それだと全体のことが考慮されていないので論文ではピクセル$(i,k)$に対して、上から決めていった時のそこまでのseamのエネルギーの合計値$A(i,k)$と通常のSeam Carvingの要領で下から求めていく最適なseamのエネルギーの合計値$X(i,k)$を使って次のように計算します（詳しくは後ほど載せるコードと照らし合わせて見てください。）

w(i,j) = \begin{cases}A(i,k)\times X(j,k+1) & (|\ i-j\ | \leq 1)\\-\infty & (other)\end{cases}

続いて、$0$番目から見ていった時に$i$番目までのピクセルの割り当てで最適なコストの合計値を$F(i)$と置きます。
これで準備が整いました。漸化式を見ていきましょう。

漸化式を考える上で注意したいのが、今回の$F(i)$の最適なコストというのが最大値という点です。Seam Carvingでは最小のエネルギーのseamから求めていったので少し違和感があるかもしれません。
ですがSeam Carvingの最小のエネルギーのseamから消していくというのは、すなわち残っている画像のエネルギーの合計値を最大にするという意味になります。そのため、割り当てを考える時も一個消したとしてもなるべく大きいコストが残るように、というわけで最大値を求めるわけです。

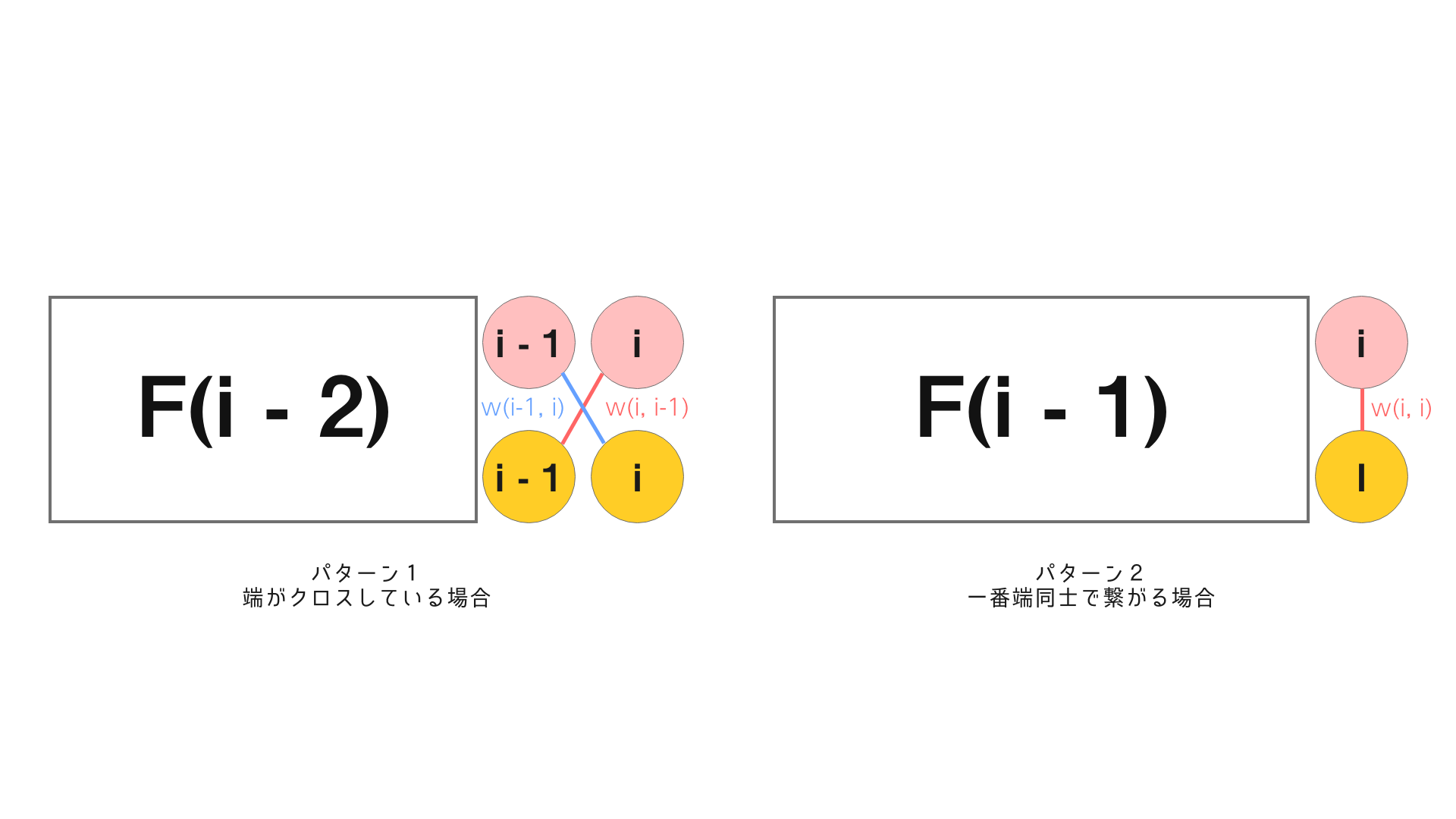
さて具体的な式ですが、これは図のように先程紹介した２パターンがあることに注目すればあとは簡単です。この時それぞれの割り当ての仕方のコストの合計値は新しくつくった繋がりのコストとそれまでのコストの最大値の和ということになります。これによって次のような式が成り立ちます。

F(i) = \max\{F(i-1)+w(i,i), F(i-2)+w(i,i-1)+w(i-1,i)\}

これで計算完了です！あとはSeam Carvingの時と同じ要領で右端から求めた$F$の値を使って実際の繋がりがどうなっているのかを求めていきます。

最後にこの計算結果に基づいてソートなどをしながらすべてのピクセルが何番目に消されるのかを求めていけば高速でConsistent Index Mapが計算できます。大体600×402の画像で縦横求めるのに200ms程度で計算できました（とはいえメモリのことやナイーブな実装でJSということもあり、4000×3000など最近の高画質画像にはたちうち出来ないのですが...）

実際のコードがこちらです。$F(-1)$、$F(-2)$などのことを考慮してすこし添え字が煩雑になってしまっているのですが大体こんな感じです。

calculateVerticalSeamMap(heatMap: number[][]) {
  const width = this.imageData.width;
  const height = this.imageData.height;

  // For calculating weights by the method of Real-time content-aware image resizing(2009)
  let A: number[][] = [];
  let M: number[][] = [];
  let mMap: number[][] = []; // for backtrack

  for (let j = 0; j <= height; j++) {
    M[j] = new Array<number>(width);
  }

  // Calculate M by dynamic programming
  for (let i = 0; i < width; i++) {
    M[height][i] = 0;
  }
  for (let j = height - 1; j >= 0; j--) {
    for (let i = 0; i < width; i++) {
      const vl = i - 1 >= 0 ? M[j + 1][i - 1] : inf;
      const vm = M[j + 1][i];
      const vr = i + 1 < width ? M[j + 1][i + 1] : inf;
      M[j][i] = heatMap[j][i] + Math.min(vl, vm, vr);
    }
  }

  // Set A[0] is energy
  A[0] = heatMap[0].slice();

  // Frist compute best 1-edge path for all pairs of rows
  let weight: number[][] = [];
  for (let i = 0; i <= width; i++) {
    weight[i] = [];
    for (let j = 0; j <= width; j++) {
      weight[i][j] = minf;
    }
  }
  for (let k = 0; k < height - 1; k++) {
    A[k + 1] = new Array(width);
    mMap[k] = new Array(width);
    // compute weight
    for (let i = 1; i <= width; i++) {
      for (let j = Math.max(i - 1, 1); j <= Math.min(i + 1, width); j++) {
        weight[i][j] = A[k][i - 1] * M[k + 1][j - 1];
      }
    }

    // calculate F(m)
    let f: number[] = [];
    f[0] = 0;
    const getF = (i: number) => {
      if (i === -1) {
        return 0;
      }
      return f[i];
    }
    for (let i = 1; i <= width; i++) {
      let f1 = getF(i - 1) + weight[i][i];
      let f2 = getF(i - 2) + weight[i - 1][i] + weight[i][i - 1];
      f[i] = Math.max(f1, f2);
    }
    // Solve the optimal matching and update A
    let x = width;
    while (x > 1) {
      let f1 = getF(x - 1) + weight[x][x];
      let f2 = getF(x - 2) + weight[x - 1][x] + weight[x][x - 1];
      if (f1 > f2) {
        // m(i,k) = i
        mMap[k][x - 1] = x - 1;
        A[k + 1][x - 1] = heatMap[k + 1][x - 1] + A[k][x - 1];
        x -= 1;
      } else {
        // m(i,k) = i-1, m(i-1,k) = i
        mMap[k][x - 1] = x - 2;
        mMap[k][x - 2] = x - 1;
        A[k + 1][x - 1] = heatMap[k + 1][x - 1] + A[k][x - 2];
        A[k + 1][x - 2] = heatMap[k + 1][x - 2] + A[k][x - 1];
        x -= 2;
      }
    }
    if (x === 1) {
      mMap[k][0] = 0;
      A[k + 1][0] = heatMap[k + 1][0] + A[k][0];
    }
  }

  let addr: number[] = [];
  for (let x = 0; x < width; x++) {
    addr[x] = x;
  }

  // Quicksort last row
  const quickSort = (arr: number[], left: number, right: number) => {
    let pivot = 0;
    let partitionIndex = 0;
    if (left < right) {
      pivot = right;
      partitionIndex = partition(arr, pivot, left, right);
      quickSort(arr, left, partitionIndex - 1);
      quickSort(arr, partitionIndex + 1, right);
    }
  }
  const partition = (arr: number[], pivot: number, left: number, right: number) => {
    const pivotValue = arr[pivot];
    let partitionIndex = left;

    for (let i = left; i < right; i++) {
      if (arr[i] < pivotValue) {
        swap(arr, i, partitionIndex);
        partitionIndex += 1;
      }
    }
    swap(arr, right, partitionIndex);
    return partitionIndex;
  }
  const swap = (arr: number[], i: number, j: number) => {
    const temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
    const temp2 = addr[i];
    addr[i] = addr[j];
    addr[j] = temp2;
  }
  quickSort(A[height - 1], 0, width - 1);

  // Backtrack and consist consistentVerticalMap
  for (let x = 0; x < width; x++) {
    this.consistentVerticalMap[height - 1][addr[x]] = x + 1;
  }
  for (let y = height - 1; y >= 1; y--) {
    for (let x = 0; x < width; x++) {
      this.consistentVerticalMap[y - 1][mMap[y - 1][x]] = this.consistentVerticalMap[y][x];
    }
  }
  return mMap;
}

4. Conclusion

今回の記事では画像処理の基本、動的計画法、そしてSeam Carvingとその高速化手法についてを紹介してみました。画像処理というと最近のトレンドでは機械学習を使うものというイメージを持ちがちですが、このようにとても単純な操作だけでここまで不思議なことができてしまうということを少しでも体感していただけたなら、良かったんじゃないかなと思います。

なんだか比較対象として機械学習を出してしまいましたが、実はこのことは機械学習についても言えて、機械学習もちゃんと仕組みを見ていけばすごく単純なことしかしてないのになぜだかあんなにすごいことが出来てしまう代表格かなと思っています。

そういうパっと見すごく単純なことをするだけで魔法のようなことが次々と出来てしまう、それこそがプログラミングの力であり、コンピューターサイエンスの力であると思うのでこの機会にぜひみなさんも、興味のわいた分野からでいいので、コンピューターサイエンスを学んでみてはいかがでしょうか？

というわけで長文でしたが最後まで読んでいただいた方ありがとうございました！明日はUnityのドン、そしてゲーム企画のプロであるじゅんじゅんの記事です。アドベントカレンダーも残りわずか、クリキャンも近くなってきましたがぜひみんなで走り抜けていければと思います🙌

1. Seam Carving for Content-Aware Image Resizing - 2007 - Avidan S, Shamir A. ↩

2. Real-time content-aware image resizing - 2009 - HUANG Hua, FU TianNan, ROSIN Paul L. & QI Chun ↩

3. ちなみに本記事のすべての図はタイトル画像を含めてAdobe XDのみを使用して制作しています。最近Adobe XDでいろんなことをやってみるというのが流行りですが、しっかりグラフィックもこのレベルで出来てしまうのはいいですね。 ↩

4. こちらを解説している記事もなかなか少なく、英語の記事しかないのですがMatlabのコード付きなので興味のある方はこちらを見てください。 ↩

5. これはオーダー記法というものです。詳しく知りたい方はぜひ調べてみてください。拙作ですが一応二年前の同アドベントカレンダーでも少し解説しているのでよければどうぞ ↩