異常検知について勉強したのでまとめておきます。
参考文献
下記文献を大いに参考にさせていただきました:
[1] Ruff, Lukas, et al. "A Unifying Review of Deep and Shallow Anomaly Detection." arXiv preprint arXiv:2009.11732 (2020).
[2] 井手. "入門 機械学習による異常検知―Rによる実践ガイド" コロナ社(2015)
[3] 井手,杉山. "異常検知と変化検知 (機械学習プロフェッショナルシリーズ)" 講談社サイエンティフィク(2015)
[4] 比戸. "異常検知入門" Jubatus Casual Talks #2(2013)
[5] Pang, Guansong, et al. "Deep learning for anomaly detection: A review." arXiv preprint arXiv:2007.02500 (2020).
§1 異常検知の概要
異常検知の適応例
- 医療×異常検知
医療用画像からの疾患部位の特定

出典:Thomas, et al.Unsupervised Anomaly Detection with Generative Adversarial Networks to Guide Marker Discovery
- 金融×異常検知
マネーロンダリング検知

出典:Mark, et al.Anti-Money Laundering in Bitcoin: Experimenting with Graph Convolutional Networks for Financial Forensics
異常は多種多様にわたる
異常と一口に言っても多種多様な異常があり、大きく静的な異常と動的な異常に分けられます(私が勝手に作った切り口なのでおかしな点があればご指摘ください)。
静的な異常とは、各データ間に順序性等の関係がなく、データの値が異常の尺度になるものをいいます。
- 例えば,医療用画像において該当部位の濃淡が健康な場合のそれと大きく異なる場合に異常(疾患の存在)と判断されます。
- このような静的な異常は特に外れ値(Outlier)と呼んだりします。
動的な異常とは、時系列データのようにデータ間に順序性等の関係があり、データの振る舞いが異常の尺度になるものをいいます。
- 振る舞いが異常であるとは,同一区間での観測値の増減が激しかったり逆に変化が著しく小さくなったりと個々の問題に依存します。
- 静的な異常との大きな違いは,動的な異常は値そのものが異常であるとは限らない点です。
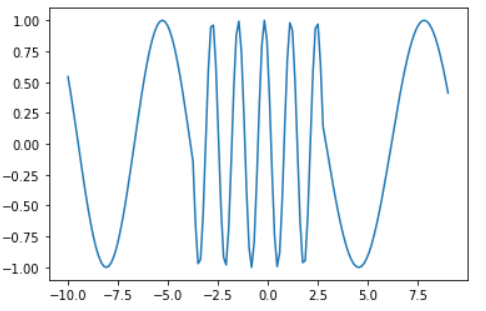
- 例えば,下グラフの中央部は異常のように見えますが、値自体は取り得る値です。このケースでは、「周波数の変化」という振る舞いに異常性を見出すことになります。
import numpy as np
import matplotlib.pyplot as plt
x1 = np.concatenate([np.linspace(-10, -3, 50), np.zeros(50), np.linspace(3, 9, 50)])
x2 = np.concatenate([np.zeros(50), np.linspace(-3, 3, 50), np.zeros(50)])
y = np.sin(x1) + np.sin(5*x2)
plt.plot(np.linspace(-10, 9, 150), y)
数式で表現すると、系列データ$\{x_1, ..., x_t\}$において各点$x_j$が$p(x)=\int p(x,t){\rm d}t$の意味で正常であっても、時間の条件付き確率$p(x_j \mid t) = \int \cdots \int p(x_1,...x_t \mid t){\rm d}t_1 \cdots {\rm d}t_{j-1}{\rm d}t_{j+1}\cdots{\rm d}t_t$においては異常となり得えます。
ただしこのケースにおいても、中央部が異常ではない場合もあります。 例えば、上グラフが工場の機械動作シグナルであり中央部だけオペレーションモードが切り替わっていたため異常ではないということも考えられます。
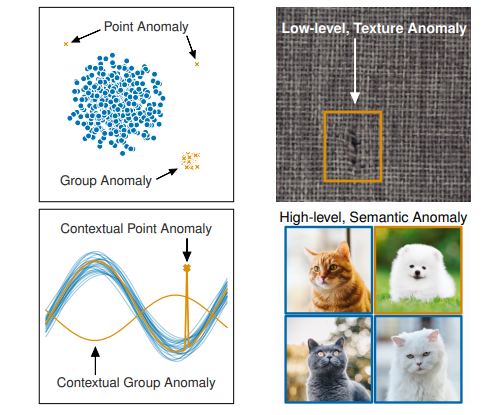
以上のように異常には色々な側面がありますが、文献[1]ではこのように異常の種類をまとめています:
左上図のPoint Anomalyは観測エラー等による単発ノイズデータ(外れ値)に見えますが、Group Anomalyは外れ値というよりも別の分布から発生しているデータ群に見えます。両者では異なった異常検知アプローチが必要と想定されます。右下のSemantic Anomalyまで来ると古典的な異常検知手法では対応が難しく、ディープラーニングによるアプローチが必要になってきます。
このように「異常」に統一解はなく、ケースバイケースで「異常」を定義しなければいけません。
異常検知アルゴリズムは基本的に教師なし学習である
異常検知アルゴリズムは教師あり学習ではなく基本的に教師なし学習を用います。
理由は2つで:
- 大概、異常データは少ないから
- 異常データは多種多様であり網羅的にモデリングすることが難しいから
です。特に異常がクリティカルな現場(医療や工場)では、異常データを数百~数千も集められないはずです。また、理由2に関しては冒頭で説明したとおりです。「正常・異常」を当てるよりも、「正常・正常じゃない」を当てる方が簡単で筋が良い問題設定になります。後者は異常データに関して言及しておらず、正常データの構造理解のみで達成可能です。教師なし学習とは、サンプル$x_i(i=1,...,n)$から$p(x)$を推定することでデータの構造を理解する枠組みですから、異常検知は基本的に教師なし学習を用いることになります。ただし、教師なし学習を行う際のサンプルには異常データが含まれていない、もしくは圧倒的少数であると仮定できる必要があります。
余談ですが、文献[2]では以下のようなことを述べておりお気に入りです:
トルストイの『アンナ・カレーニナ』という小説に「幸せな家族は皆どこか似ているが,不幸せな家族はそれぞれ違う(Happy families are all alike; every unhappy family is unhappy in its own way)」という一節があり示唆的です.
異常検知アルゴリズムは4種類に大別される
それでは具体的に異常検知アルゴリズムの紹介をしていきます。
アルゴリズムは大きく4つのアプローチにより分類できます。それぞれ、Classification Approach, Probabilistic Approach, Reconstruction Approach, Distance Approachです。この4つの分類に加えて、ディープラーニングを用いるか否かで分類をした表がこちらになります:
PCAやOC-SVM等のワードひとつひとつが過去提案されてきた異常検知アルゴリズムの名前です。各アルゴリズムの詳細は後続で紹介するので、ここでは4つのアプローチそれぞれの概要の紹介に留めます。(私自身、下記テーブルへの理解が十分ではないためご意見をいただけますと勉強になります。)
| アプローチ | 概要 | Pros | Cons |
|---|---|---|---|
| Classification | データの正常・異常を分ける境界を直接推定するアプローチ | 分布の形状を仮定する必要がない。また、SVMを用いた手法においては比較的少数データで学習可能。 | 正常データが複雑な構造をしていると上手く動作しない場合がある |
| Probabilistic | 正常データの確率分布を推定し、生起確率が低い事象を異常とみなすアプローチ | データが仮定したモデルに従っていれば非常に高精度を達成 | 分布モデル等多くの仮定が必要。また高次元への対応も困難。 |
| Reconstruction | 正常データを再構成するようwell-trainされたロジックが上手く再構成できないデータは異常である、というアプローチ | 近年盛んに研究されているAEやGAN等の強力な手法が適応できる。 | あくまでも次元圧縮や再構成精度を高めるために目的関数がデザインされているため、必ずしも異常検知に特化した手法ではないこと。 |
| Distance | データ間の距離に基づき異常検知を行うアプローチ。異常データは正常データから距離的に離れているという発想。 | アイディアがシンプルで、出力への説明可能性も高い。 | 計算量が大きい($O(n^2)$など) |
§2 アルゴリズムの紹介と実験
紹介する手法まとめ
- Classification Approach
- OC-SVM (One Class SVM)
- Probability Approach
- ホテリングのT2法
- GMM (Gaussian Mixture Model, 混合正規分布)
- KDE (Kernel Density Estimation, カーネル密度推定)
- Reconstruction Approach
- AE (Auto Encoder, オートエンコーダー)
- Distance Approach
- k-NN (k-Nearest Neighbor, k近傍法)
- LOF (Local Outlier Factor, 局所外れ値因子法)
Classification Approach
One-Class SVM
データ$D=\{x_1,...,x_N\}$が与えられているとします。ただし$D$には異常データが含まれていないか、含まれていたとしても圧倒的少数であるとします。
前章でClassification Approachは正常・異常を分ける境界を推定すると紹介しました。One-Class SVMは、正常データをすっぽり囲むような球を計算し境界とするアルゴリズムです。(球といっても三次元とは限りません。)
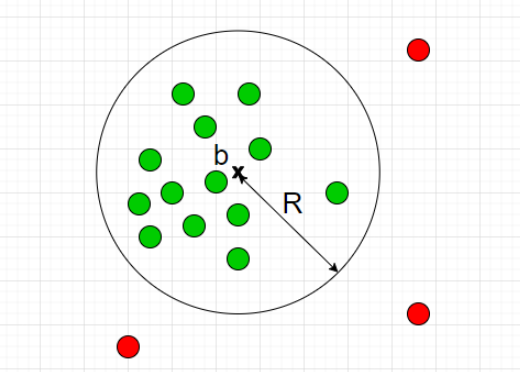
半径をとても大きくとれば$D$をすっぽり内包する球は作れますが、大きすぎる球ではFalse Negativeが1になってしまい嬉しくありません。そこで、
- 球の体積はできるだけ小さくする
- $D$のなかで、球からはみ出るデータがあることを許容する
の2点を許すことで汎用的な球を計算します。具体的には以下の最適化問題を解くことで最適な球の半径$R$と中心$b$が求まります:
\min_{R,b,u} \left\{R^2 + C\sum_{n=1}^{N}u_n \right\} \quad {\rm s.t.} \quad \|x_n - b\|^2 \le R^2 + u_n
ただし、$u$は球からはみ出した分のペナルティ項、$C$はそのペナルティをどれくらい重要視するかのパラメータです。SVMではカーネル関数によるデータの非線形変換が可能ですが、もちろんOne-Class SVMでも利用可能です。カーネル関数を適切に利用することで、適切な球が求まります。
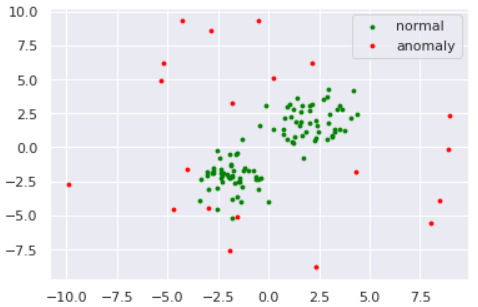
数値実験をしてみます。データは以下のように準備しました。
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
np.random.seed(123)
# 平均と分散
mean1 = np.array([2, 2])
mean2 = np.array([-2,-2])
cov = np.array([[1, 0], [0, 1]])
# 正常データの生成(2つの正規分布から生成)
norm1 = np.random.multivariate_normal(mean1, cov, size=50)
norm2 = np.random.multivariate_normal(mean2, cov, size=50)
norm = np.vstack([norm1, norm2])
# 異常データの生成(一様分布から生成)
lower, upper = -10, 10
anom = (upper - lower)*np.random.rand(20,20) + lower
s=8
plt.scatter(norm[:,0], norm[:,1], s=s, color='green', label='normal')
plt.scatter(anom[:,0], anom[:,1], s=s, color='red', label='anomaly')
plt.legend()
from sklearn import svm
xx, yy = np.meshgrid(np.linspace(-10, 10, 500), np.linspace(-10, 10, 500))
# fit the model
clf = svm.OneClassSVM(nu=0.1, kernel="rbf", gamma=0.1)
clf.fit(norm)
def draw_boundary(norm, anom, clf):
# plot the line, the points, and the nearest vectors to the plane
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
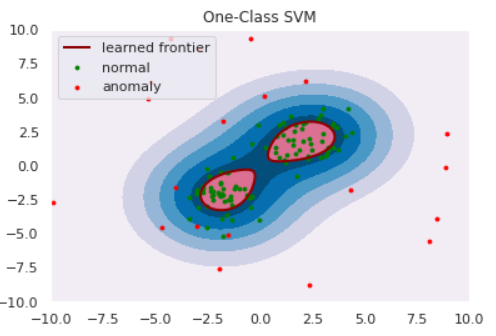
plt.title("One-Class SVM")
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), Z.max(), 7), cmap=plt.cm.PuBu)
bd = plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors='darkred')
plt.contourf(xx, yy, Z, levels=[0, Z.max()], colors='palevioletred')
nm = plt.scatter(norm[:, 0], norm[:, 1], c='green', s=s)
am = plt.scatter(anom[:, 0], anom[:, 1], c='red', s=s)
plt.axis('tight')
plt.xlim((-10, 10))
plt.ylim((-10, 10))
plt.legend([bd.collections[0], nm, am],
["learned frontier", "normal", "anomaly"],
loc="upper left",
prop=matplotlib.font_manager.FontProperties(size=11))
plt.show()
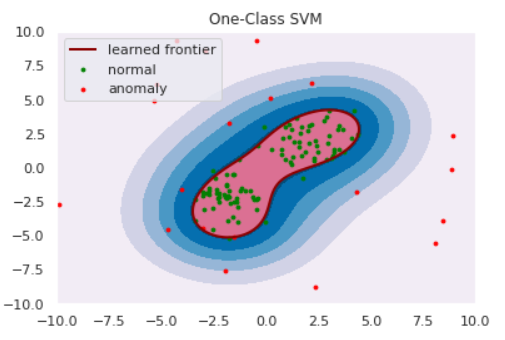
draw_boundary(norm, anom, clf)
ちなみに、パラメータ$C$を小さくする、すなわち球からはみ出すペナルティを軽くみるようにするとこのように境界が変わります。(sklearnではパラメータ$\nu$で表していますが、どうやら分母にいるらしいので$\nu$を小さくする$=C$を大きくするのようです)
# fit the model
clf = svm.OneClassSVM(nu=0.5, kernel="rbf", gamma=0.1)
clf.fit(norm)
draw_boundary(norm, anom, clf)
他にもOne-Class NN等が提案されています。One-Class SVMではカーネル関数を調整して適切な非線形変換を探索していましたが、そこをNNで代用&自動化しようというアイディアです。実装はめんどくさそうなのでやってません。
Probability Approach
ホテリングのT2法
ホテリングのT2法は古典的な手法であり、理論的な解析がなされています。 結論、正規分布を仮定することで異常度(Anomaly Score)が$\chi^2$分布に従う性質を利用したアルゴリズムになります。
ここでは簡単のため1次元データで説明します。 例によってデータ$D$が与えられているとします。ここで各データ$x$が正規分布
p(x\mid \mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{-\frac{1}{2\sigma^2}(x-\mu)^2\right\}
に従うものと仮定します。この正規分布を最尤推定法によりデータへフィッティングすることで
\begin{align*}
\hat{\mu} &= \frac{1}{N}\sum_{n=1}^{N}x_n \\
\hat{\sigma}^2 &= \frac{1}{N}\sum_{n=1}^{N}(x_n - \hat{\mu})^2
\end{align*}
と各パラメータが推定されます。つまり、データ$D$は正規分布$p(x\mid \hat{\mu}, \hat{\sigma}^2)$に従うと推定したわけです。
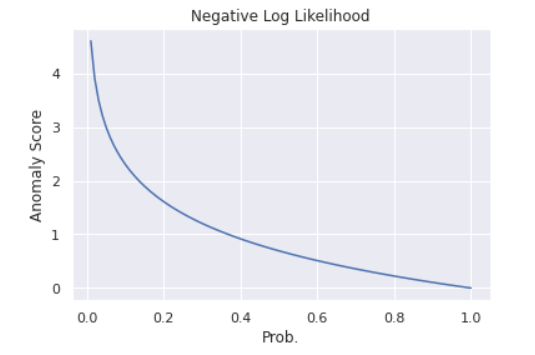
さて、ここで異常度(Anomaly Score)を導入します。異常度とは、文字通り異常の度合いを示す統計量のことで、よく負の対数尤度が用いられます。
prob = np.linspace(0.01, 1, 100)
neg_log_likh = [-np.log(p) for p in prob]
plt.plot(prob, neg_log_likh)
plt.title('Negative Log Likelihood')
plt.ylabel('Anomaly Score')
plt.xlabel('Prob.')
グラフのように、負の対数尤度は確率が小さいところで大きな値をとる形状をしており、異常度として機能しそうです。今推定した正規分布の異常度を計算すると
-\log p(x\mid \hat{\mu}, \hat{\sigma}^2) = \frac{1}{2\hat{\sigma}^2}(x-\hat{\mu})^2 + \frac{1}{2}\log(2\pi\hat{\sigma}^2)
となります。異常度はデータ$x$に対して定義される量ですから、$x$に関係ない項は除いたうえで異常度$a(x)$は
a(x) = \left( \frac{x - \hat{\mu}}{\hat{\sigma}} \right)^2
と計算されます。異常度の分子は、「データが平均から離れているほど異常度が高くなる」ということを表しています。分母は、「どれくらいデータが散らばっているか?」を表しており、散らばっているデータでは平均から遠く離れていようと大目に見る、逆に密なデータでは少しのズレも許さないというお気持ちがあります。
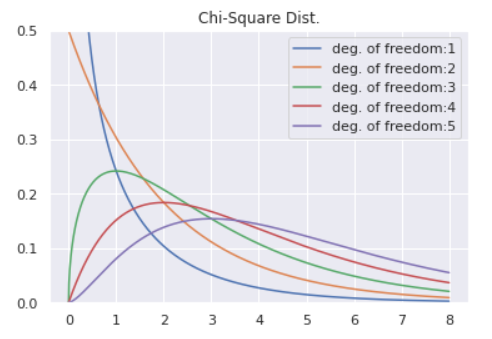
実はこの異常度$a(x)$はサンプルサイズ$N$が十分大きいときに自由度$1$のカイ二乗分布$\chi^2_1$に従うことがわかっています。
from scipy.stats import chi2
x = np.linspace(0, 8, 1000)
for df in [1,2,3,4,5]:
plt.plot(x, chi2.pdf(x ,df = df), label='deg. of freedom:'+str(df))
plt.legend()
plt.ylim(0, 0.5)
plt.title('Chi-Square Dist.')
あとは有意水準$5$%で閾値$a_{th}$を決めるなどしてあげれば異常検知が可能となります。まとめると、
- データが正規分布に従うと仮定する。
- 正規分布のパラメータ$\mu$, $\sigma$を最尤推定法により推定する
- カイ二乗分布から、正常・異常を分ける点$a_{th}$を決める
- 新たなデータ$x_{new}$が、$a(x_{new})>a_{th}$だったら異常とみなす
がホテリングのT2法です。今回は1次元で説明しましたが、多次元でも同様に異常度がカイ二乗分布に従います。ただし、自由度=次元数です。
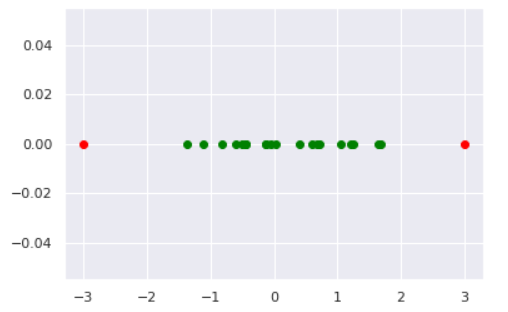
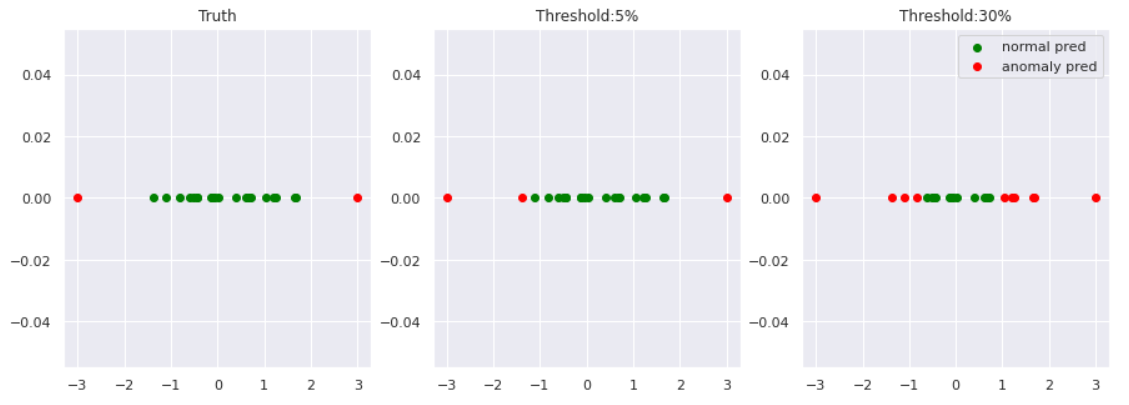
では実験してみましょう。データは以下のように作成しました。
norm = np.random.normal(0, 1, 20) # 正常データ
anom = np.array([-3, 3]) # 異常データ
plt.scatter(norm, [0]*len(norm), color='green', label='normal')
plt.scatter(anom, [0]*len(anom), color='red', label='anomaly')
# 最尤推定
N = len(norm)
mu_hat = sum(norm)/N
s_hat = sum([(x-mu_hat)**2 for x in norm])/N
# カイ二乗分布の分位点を閾値とする
a_th_5 = chi2.ppf(q=0.95, df=1)
a_th_30 = chi2.ppf(q=0.7, df=1)
# 各データの異常度を計算
data = np.hstack([norm, anom])
anom_score = []
for d in data:
score = ((d - mu_hat)/s_hat)**2
anom_score.append(score)
# 描画
norm_pred_5 = [d for d,a in zip(data, anom_score) if a<=a_th_5]
anom_pred_5 = [d for d,a in zip(data, anom_score) if a>a_th_5]
norm_pred_30 = [d for d,a in zip(data, anom_score) if a<=a_th_30]
anom_pred_30 = [d for d,a in zip(data, anom_score) if a>a_th_30]
fig, axes = plt.subplots(1,3, figsize=(15,5))
axes[0].scatter(norm, [0]*len(norm), color='green', label='normal')
axes[0].scatter(anom, [0]*len(anom), color='red', label='anomaly')
axes[0].set_title('Truth')
axes[1].scatter(norm_pred_5, [0]*len(norm_pred_5), color='green', label='normal pred')
axes[1].scatter(anom_pred_5, [0]*len(anom_pred_5), color='red', label='anomaly pred')
axes[1].set_title('Threshold:5%')
axes[2].scatter(norm_pred_30, [0]*len(norm_pred_30), color='green', label='normal pred')
axes[2].scatter(anom_pred_30, [0]*len(anom_pred_30), color='red', label='anomaly pred')
axes[2].set_title('Threshold:30%')
plt.legend()
異常度の閾値を小さくすれば、異常と見なされる区域が広がっていくことが見て取れます。
閾値は問題に応じて決める必要があります。例えば、医療の現場など異常の見逃しがクリティカルな場合は閾値は小さく設定すべきですし、データクレンジング等の場合はもう少し大きい閾値にしてもいいかもしれません。
GMM(Gaussian Mixture Model)
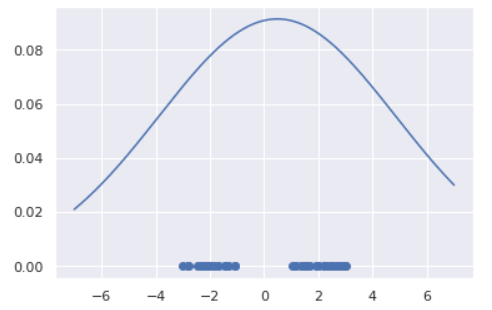
ホテリングのT2法ではデータに正規分布を仮定していましたが、これが不適切なケースもあるでしょう。例えば以下のようにデータが複数個所に集中している(単峰ではなく多峰)場合に正規分布でフィッティングすると
lower, upper = -3, -1
data1 = (upper - lower)*np.random.rand(20) + lower
lower, upper = 1, 3
data2 = (upper - lower)*np.random.rand(30) + lower
data = np.hstack([data1, data2])
# 最尤推定
N = len(data)
mu_hat = sum(data)/N
s_hat = sum([(x-mu_hat)**2 for x in data])/N
# プロット
from scipy.stats import norm
X = np.linspace(-7, 7, 1000)
Y = norm.pdf(X, mu_hat, s_hat)
plt.scatter(data, [0]*len(data))
plt.plot(X, Y)
のように、全くデータが観測されていない箇所に正規分布のピークが来るように推定されてしまいます。こういった場合は正規分布ではなく、もう少し複雑な分布を設定するのが良いでしょう。今回はその一例としてGMM(Gaussian Mixture Model, 混合正規分布)による異常検知を紹介します。
GMMとは正規分布をいくつか足し合わせることで多峰型を表現する分布です。足し合わせる個数はよく$K$で表現され、コンポーネント数と呼ばれます。GMMの数式とビジュアルは以下の通りです(1次元にしています)。
p(x\mid \pi, \mu, \sigma) = \sum_{k=1}^{K}\pi_k N(x\mid \mu_k, \sigma_k)
ただし、
0 \le\pi_k\le 1,\quad \sum_{k=1}^{K}\pi_k=1,\quad N(x\mid\mu,\sigma)={\text 正規分布}
です。
# プロット
from scipy.stats import norm
X = np.linspace(-7, 7, 1000)
Y1 = norm.pdf(X, 1, 1)
Y2 = norm.pdf(X, -3, 2)
Y = 0.5*Y1 + 0.5*Y2
plt.plot(X, Y1, label='Component1')
plt.plot(X, Y2, label='Component2')
plt.plot(X, Y, label='GMM')
plt.legend()
各正規分布の平均($\mu$)・分散($\sigma$)と、混合率$\pi$はデータから学習されるパラメータです。しかしコンポーネント数$K$は決め打ちする必要があります。このように分析者側で決め打ちにするパラメータをハイパーパラメータと呼びます。
ではGMMによる異常検知を実験してみます。コンポーネント数$K$によってどのように推定分布の形状が変わるのかも観察しましょう。データはOne-Class SVMと同様以下を使用します。
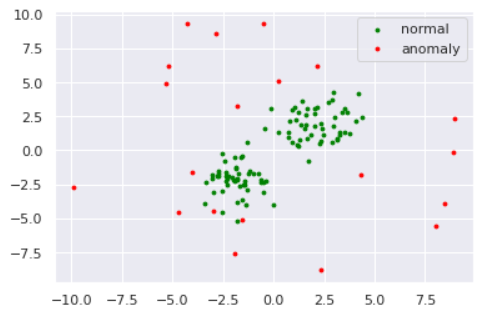
def draw_GMM(norm, anom, clf, K):
# plot the line, the points, and the nearest vectors to the plane
xx, yy = np.meshgrid(np.linspace(-10, 10, 1000), np.linspace(-10, 10, 1000))
Z = np.exp(clf.score_samples(np.c_[xx.ravel(), yy.ravel()]))
Z = Z.reshape(xx.shape)
plt.title("GMM:K="+str(K))
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), Z.max(), 7), cmap=plt.cm.PuBu)
nm = plt.scatter(norm[:, 0], norm[:, 1], c='green', s=s)
am = plt.scatter(anom[:, 0], anom[:, 1], c='red', s=s)
plt.axis('tight')
plt.xlim((-10, 10))
plt.ylim((-10, 10))
plt.legend([nm, am],
["normal", "anomaly"],
loc="upper left",
prop=matplotlib.font_manager.FontProperties(size=11))
plt.show()
# GMMによるフィッティング
from sklearn.mixture import GaussianMixture
for K in [1,2,3,4]:
clf = GaussianMixture(n_components=K, covariance_type='full')
clf.fit(norm)
draw_GMM(norm, anom, clf, K)
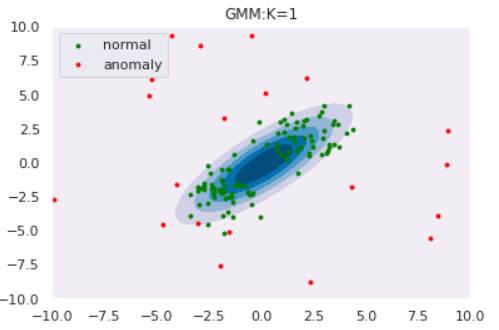
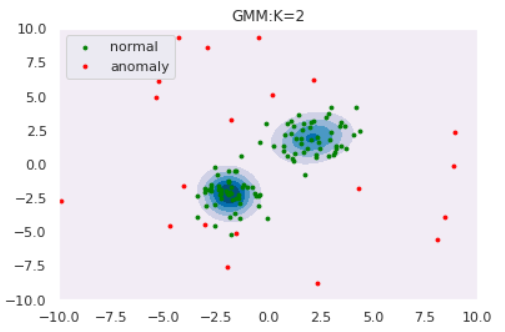
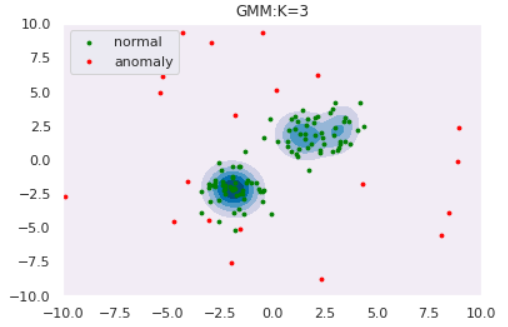
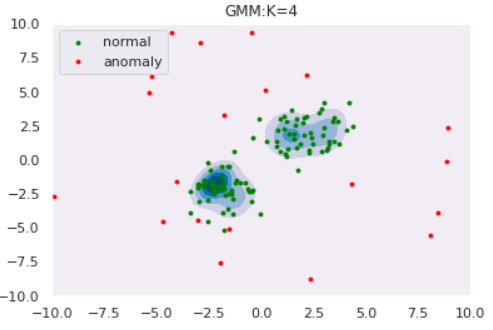
このようにコンポーネント数を多くすると、データの細部の傾向まで捉えていることがわかります。しかし、細部まで捉えている=汎化性能が高いわけではないので注意が必要です。コンポーネント数はWAIC等の情報量規準を用いて決定することができます(とりあえずWAICを使ってみました:GitHub)
KDE(Kernel Density Estimation)
今までは正規分布や混合正規分布を仮定し、データへのフィッティングを通じて内部パラメータの推定を行ってきました。このようなアプローチをパラメトリックなアプローチといいます。しかし、パラメトリックな分布では上手く表現できないような場合にはどうしたら良いでしょうか?
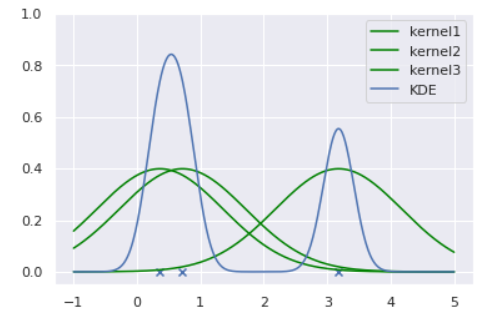
ノンパラメトリックなアプローチはそのような場合に有効であり、KDEは代表的なノンパラメトリック推定手法です。KDEは、各データ点にカーネル(通常はGaussian)を重ねることで確率分布を推定する手法です。可視化すると以下のようになります。
from scipy.stats import norm
np.random.seed(123)
lower, upper = -1, 5
data = (upper - lower)*np.random.rand(3) + lower
for i, d in enumerate(data):
X = np.linspace(lower,upper,500)
Y = norm.pdf(X, loc=d, scale=1)
knl = plt.plot(X,Y,color='green', label='kernel'+str(i+1))
# KDE
n = 3
h = 0.24
Y_pdf = []
for x in X:
Y = 0
for d in data:
Y += norm.pdf((x-d)/h, loc=0, scale=1)
Y /= n*h
Y_pdf.append(Y)
kde = plt.plot(X,Y_pdf, label='KDE')
plt.scatter(data, [0]*len(data), marker='x')
plt.ylim([-0.05, 1])
plt.legend()
このようにカーネルの重ね合わせで確率分布を推定しています。カーネルに正規分布を用いる場合は分散(バンド幅と呼びます)を決め打ちする必要があります。後続の実験では、このバンド幅を変えた時の推定分布の変化も観察しましょう。
KDEの理論詳細および長所・短所は鈴木.データ解析第十回「ノンパラメトリック密度推定法」がわかりやすかったです:
推定分布
p(x) = \frac{1}{Nh}\sum_{n=1}^{N}K\left(\frac{x-X_n}{h}\right)
ただし、$h>0$をバンド幅、$K()$をカーネル関数、$X_n$は各データ点とする。
長所・短所

出典:鈴木.データ解析第十回「ノンパラメトリック密度推定法」
ではKDEによる異常検知を実験してみましょう。データは例によって
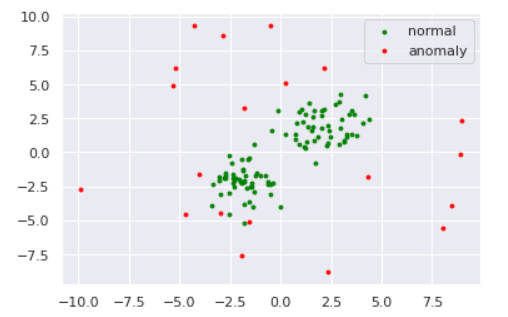
を使用します。バンド幅を変えた時の推定分布は以下のようになりました。
def draw_KDE(norm, anom, clf, K):
# plot the line, the points, and the nearest vectors to the plane
xx, yy = np.meshgrid(np.linspace(-10, 10, 1000), np.linspace(-10, 10, 1000))
Z = np.exp(clf.score_samples(np.c_[xx.ravel(), yy.ravel()]))
Z = Z.reshape(xx.shape)
plt.title("KDE:BandWidth="+str(bw))
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), Z.max(), 7), cmap=plt.cm.PuBu)
nm = plt.scatter(norm[:, 0], norm[:, 1], c='green', s=s)
am = plt.scatter(anom[:, 0], anom[:, 1], c='red', s=s)
plt.axis('tight')
plt.xlim((-10, 10))
plt.ylim((-10, 10))
plt.legend([nm, am],
["normal", "anomaly"],
loc="upper left",
prop=matplotlib.font_manager.FontProperties(size=11))
plt.show()
from sklearn.neighbors import KernelDensity
for bw in [0.2,0.5,1.0,2.0]:
clf = KernelDensity(bandwidth=bw, kernel='gaussian')
clf.fit(norm)
draw_KDE(norm, anom, clf, bw)

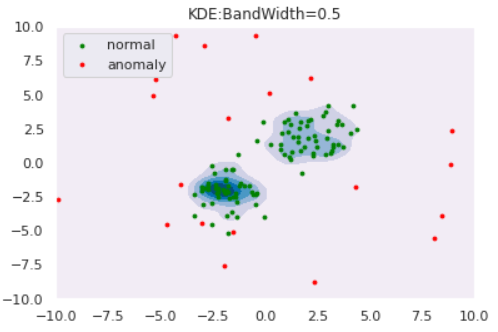
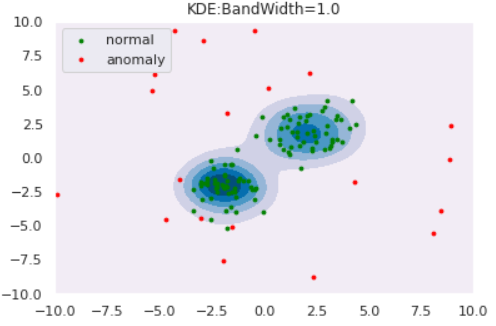
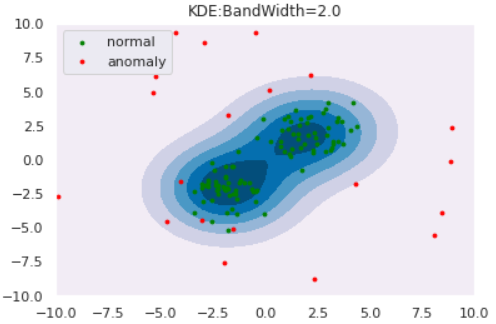
このように、バンド幅が大きくなると推定分布が滑らかになることがわかります。また、カーネル関数は正規分布に限らず他にもあるので、「バンド幅・カーネル関数」の両者を適切に設定してあげる必要があります。
Reconstruction Approach
Reconstruction Approachは画像データに用いられることが多いので、ここでも画像データを使用します。正常データをMNIST、異常データをFashion-MNISTとします。
# MNISTのロード
import torch
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
# 学習データの読み込み
train_mnist = datasets.MNIST(
root="./data",
train=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,)) # 区間[-1,1]内で平均、標準偏差 = 0.5, 0.5に正規化
]),
download=True
)
train_mnist_loader = torch.utils.data.DataLoader(
train_mnist, batch_size=64, shuffle=True
)
# テストデータの読み込み
test_mnist = datasets.MNIST(
root="./data",
train=False,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,)) # 区間[-1,1]内で平均、標準偏差 = 0.5, 0.5に正規化
]),
download=True
)
test_mnist_loader = torch.utils.data.DataLoader(
test_mnist, batch_size=64, shuffle=True
)
# Fashion-MNISTのロード
# 学習データの読み込み
train_fashion = datasets.FashionMNIST(
root="./data",
train=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,)) # 区間[-1,1]内で平均、標準偏差 = 0.5, 0.5に正規化
]),
download=True
)
train_fashion_loader = torch.utils.data.DataLoader(
train_fashion, batch_size=64, shuffle=True
)
# テストデータの読み込み
test_fashion = datasets.FashionMNIST(
root="./data",
train=False,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,)) # 区間[-1,1]内で平均、標準偏差 = 0.5, 0.5に正規化
]),
download=True
)
test_fashion_loader = torch.utils.data.DataLoader(
test_fashion, batch_size=64, shuffle=True
)
import matplotlib.pyplot as plt
# 画像を一気に並べて可視化する関数
def imshow(image_set, nrows=2, ncols=10):
plot_num = nrows * ncols
fig, ax = plt.subplots(ncols=ncols, nrows=nrows, figsize=(15, 15*nrows/ncols))
ax = ax.ravel()
for i in range(plot_num):
ax[i].imshow(image_set[i].reshape(28, 28), cmap='gray')
ax[i].set_xticks([])
ax[i].set_yticks([])
# MNISTのサンプル可視化
imshow(train_mnist.data)
# Fashion-MNISTのサンプル可視化
imshow(train_fashion.data)
AE(Auto Encoder)
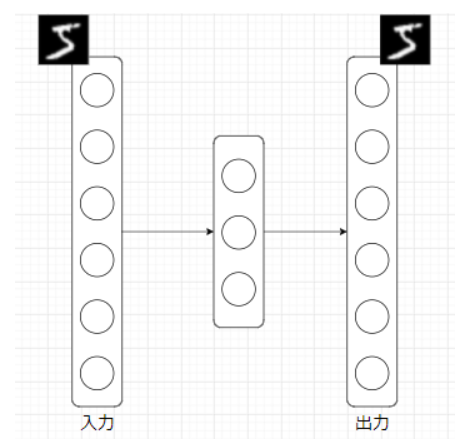
AE(Auto Encoder, オートエンコーダ)とは、NN(Neural Network, ニューラルネットワーク)の一種であり、入力と出力が等しくなるように学習するNNです。ただの恒等関数ではつまらないので、通常は入力次元よりも小さい次元の中間層を挟みます。
これは何をしているのかというと、中間層で入力データを「要約」しています。数理的には、入力データを再構成できるだけの情報を保持しつつ低次元空間へマッピングしている、ということになります。
AEを用いた異常検知は、「正常データを再構成するよう訓練されたAEは、異常データを上手く再構成できないのではないか?」という思想に基づきます。
では、AEによる異常検知を実験しましょう。AEをMNISTで訓練した後に、MNISTおよびFashion-MNISTの再構成精度を異常度として検知を試みます。
import torch.nn as nn
import torch.nn.functional as F
# AEの定義
class AE(nn.Module):
def __init__(self):
super(AE, self).__init__()
self.fc1 = nn.Linear(28*28, 256)
self.fc2 = nn.Linear(256, 28*28)
def forward(self, x):
x = torch.tanh(self.fc1(x))
x = torch.tanh(self.fc2(x))
return x
ae = AE()
# 損失関数と最適化手法の定義
import torch.optim as optim
criterion = nn.MSELoss()
optimizer = optim.Adam(ae.parameters(), lr=0.0001)
# 学習ループ
N_train = train_mnist.data.shape[0]
N_test = test_mnist.data.shape[0]
train_loss = []
test_loss = []
for epoch in range(10):
# Train step
running_train_loss = 0.0
for data in train_mnist_loader:
inputs, _ = data
inputs = inputs.view(-1, 28*28)
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = ae(inputs)
loss = criterion(outputs, inputs)
loss.backward()
optimizer.step()
running_train_loss += loss.item()
running_train_loss /= N_train
train_loss.append(running_train_loss)
# Test step
with torch.no_grad():
running_test_loss = 0
for data in test_mnist_loader:
inputs, _ = data
inputs = inputs.view(-1, 28*28)
outputs = ae(inputs)
running_test_loss += criterion(outputs, inputs).item()
running_test_loss /= N_test
test_loss.append(running_test_loss)
if (epoch+1)%1==0: # print every 1 epoch
print('epoch:{}, train_loss:{}, test_loss:{}'.format(epoch + 1, running_train_loss, running_test_loss))
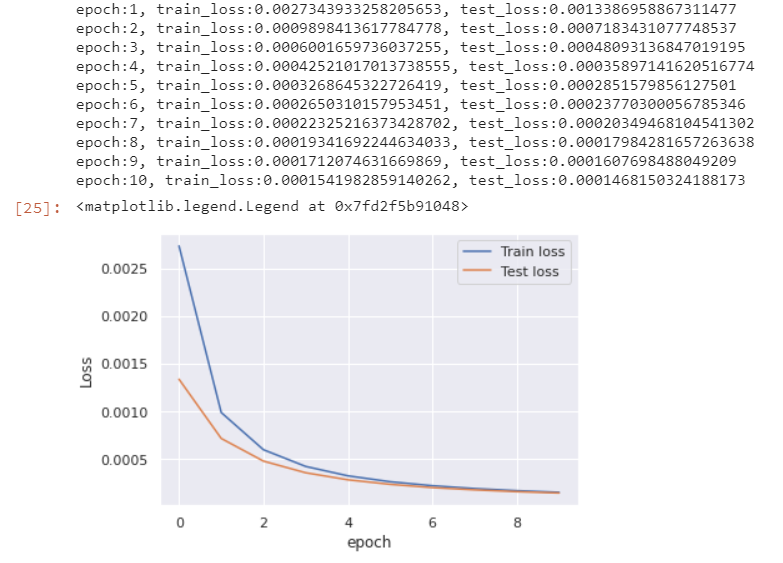
plt.plot(train_loss, label='Train loss')
plt.plot(test_loss, label='Test loss')
plt.ylabel('Loss')
plt.xlabel('epoch')
plt.legend()
# 再構成の様子を可視化してみる
with torch.no_grad():
for data in test_mnist_loader:
inputs, _ = data
inputs = inputs.view(-1, 28*28)
outputs = ae(inputs)
n = 5 # num to viz
fig, axes = plt.subplots(ncols=n, nrows=2, figsize=(15, 15*2/n))
for i in range(n):
axes[0, i].imshow(inputs[i].reshape(28, 28), cmap='gray')
axes[1, i].imshow(outputs[i].reshape(28, 28), cmap='gray')
axes[0, i].set_title('Input')
axes[1, i].set_title('Reconstruct')
axes[0, i].set_xticks([])
axes[0, i].set_yticks([])
axes[1, i].set_xticks([])
axes[1, i].set_yticks([])
きれいに再構成できていそうです。
それでは、MNISTとFashion-MNISTの再構成精度(今回は二乗誤差)の分布を描いてみます。AEによる異常検知が成功していれば、Fashion-MNISTの精度は低くなるはずです。
# 再構成精度の算出
mnist_loss = []
with torch.no_grad():
for data in test_mnist_loader:
inputs, _ = data
for data_i in inputs:
data_i = data_i.view(-1, 28*28)
outputs = ae(data_i)
loss = criterion(outputs, data_i)
mnist_loss.append(loss.item())
fashion_loss = []
with torch.no_grad():
for data in test_fashion_loader:
inputs, _ = data
for data_i in inputs:
data_i = data_i.view(-1, 28*28)
outputs = ae(data_i)
loss = criterion(outputs, data_i)
fashion_loss.append(loss.item())
plt.hist([mnist_loss, fashion_loss], bins=25, label=['MNIST', 'Fashion-MNIST'])
plt.xlabel('Loss')
plt.ylabel('data count')
plt.legend()
plt.show()
確かにFashion-MNISTの再構成は上手くいってなさそうなので、再構成精度による異常検知は成立しそうです。
最後に、Fashion-MNISTの中でもLossが低いもの(=異常と判定し辛いもの)と高いもの(=簡単に異常と判定できるもの)をピックアップして描画してみます。
lower_loss, upper_loss = 0.1, 0.8
data_low = [] # Lossが低いデータを格納
data_up = [] # Lossが高いデータを格納
with torch.no_grad():
for data in test_fashion_loader:
inputs, _ = data
for data_i in inputs:
data_i = data_i.view(-1, 28*28)
outputs = ae(data_i)
loss = criterion(outputs, data_i).item()
if loss<lower_loss:
data_low.append([data_i, outputs, loss])
if loss>upper_loss:
data_up.append([data_i, outputs, loss])
# ランダムに描画する用のインデックス
np.random.seed(0)
n = 3 #描画データ数
lower_indices = np.random.choice(np.arange(len(data_low)), n)
upper_indices = np.random.choice(np.arange(len(data_up)), n)
indices = np.hstack([lower_indices, upper_indices])
fig, axes = plt.subplots(ncols=n*2, nrows=2, figsize=(15, 15*2/(n*2)))
# Lossが小さいデータの描画
for i in range(n):
inputs = data_low[indices[i]][0]
outputs = data_low[indices[i]][1]
loss = data_low[indices[i]][2]
axes[0, i].imshow(inputs.reshape(28, 28), cmap='gray')
axes[1, i].imshow(outputs.reshape(28, 28), cmap='gray')
axes[0, i].set_title('Input')
axes[1, i].set_title('Small Loss={:.2f}'.format(loss))
axes[0, i].set_xticks([])
axes[0, i].set_yticks([])
axes[1, i].set_xticks([])
axes[1, i].set_yticks([])
# Lossが大きいデータの描画
for i in range(n, 2*n):
inputs = data_up[indices[i]][0]
outputs = data_up[indices[i]][1]
loss = data_up[indices[i]][2]
axes[0, i].imshow(inputs.reshape(28, 28), cmap='gray')
axes[1, i].imshow(outputs.reshape(28, 28), cmap='gray')
axes[0, i].set_title('Input')
axes[1, i].set_title('Large Loss={:.2f}'.format(loss))
axes[0, i].set_xticks([])
axes[0, i].set_yticks([])
axes[1, i].set_xticks([])
axes[1, i].set_yticks([])
plt.tight_layout()
Lossが低い画像は黒い面積が大きい傾向が見られる一方で、Lossが高い画像は白い面積が大きい傾向が見られます。MNISTは基本的に黒の面積が大きい画像ですので、白の面積が大きいとAEにとっては「異質」になり再構成が上手くいっていないと思われます。
Distance Approach
k-NN(k-Nearest Neighbor)
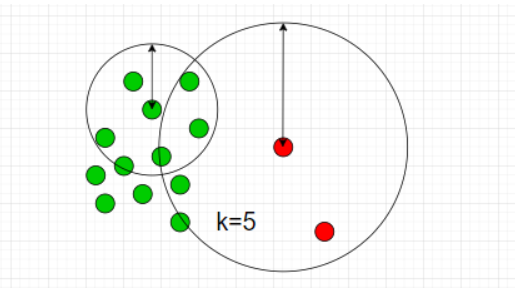
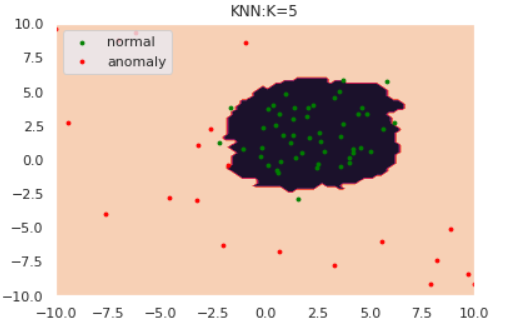
k-NNはデータ間の距離に基づき異常度を測る手法です。k-NNでは近傍のk個のデータ点を含むような円を考えます。下図は$k=5$の場合です。
図のように、「異常データが描く円は正常データよりも大きくなるはず」とう思想に基づきk-NNでは円の半径を異常度として定義します。ただし、近傍点の個数$k$と正常/異常を分ける半径の閾値は適切にチューニングする必要があります。
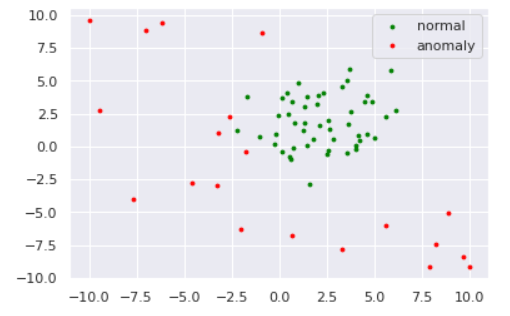
それでは数値実験を行います。閾値は、正常データの半径値分布における90%分位点とします。
# データの作成
np.random.seed(123)
# 平均と分散
mean = np.array([2, 2])
cov = np.array([[3, 0], [0, 3]])
# 正常データの生成
norm = np.random.multivariate_normal(mean1, cov, size=50)
# 異常データの生成(一様分布から生成)
lower, upper = -10, 10
anom = (upper - lower)*np.random.rand(20,20) + lower
s=8
plt.scatter(norm[:,0], norm[:,1], s=s, color='green', label='normal')
plt.scatter(anom[:,0], anom[:,1], s=s, color='red', label='anomaly')
plt.legend()
k-NNによる異常検知を、どのようにライブラリで完結できるか分からなかったので自作します。。。
# 全データのk近傍円の半径を計算する関数
def kNN(data, k=5):
"""
input: data:list, k:int
output: 全データのk近傍円の半径:list
距離はユークリッド距離を採用します。
"""
output = []
for d in data:
distances = []
for p in data:
distances.append(np.linalg.norm(d - p))
output.append(sorted(distances)[k])
return output
# 閾値より大きければ1, 小さければ0を返す関数
def kNN_scores(point, data, thres, K):
distances = []
for p in data:
distances.append(np.linalg.norm(point - p))
dist = sorted(distances)[K]
if dist > thres:
return 1
else:
return 0
def draw_KNN(norm, anom, thres, K, only_norm=False):
# plot the line, the points, and the nearest vectors to the plane
xx, yy = np.meshgrid(np.linspace(-10, 10, 100), np.linspace(-10, 10, 100))
Z = [kNN_scores(point, norm, thres, K) for point in np.c_[xx.ravel(), yy.ravel()]]
Z = np.array(Z).reshape(xx.shape)
plt.title("KNN:K="+str(K))
plt.contourf(xx, yy, Z)
if not only_norm:
nm = plt.scatter(norm[:, 0], norm[:, 1], c='green', s=s)
am = plt.scatter(anom[:, 0], anom[:, 1], c='red', s=s)
plt.axis('tight')
plt.xlim((-10, 10))
plt.ylim((-10, 10))
plt.legend([nm, am],
["normal", "anomaly"],
loc="upper left",
prop=matplotlib.font_manager.FontProperties(size=11))
if only_norm:
nm = plt.scatter(norm[:, 0], norm[:, 1], c='green', s=s)
plt.axis('tight')
plt.xlim((-10, 10))
plt.ylim((-10, 10))
plt.legend([nm],
["normal"],
loc="upper left",
prop=matplotlib.font_manager.FontProperties(size=11))
plt.show()
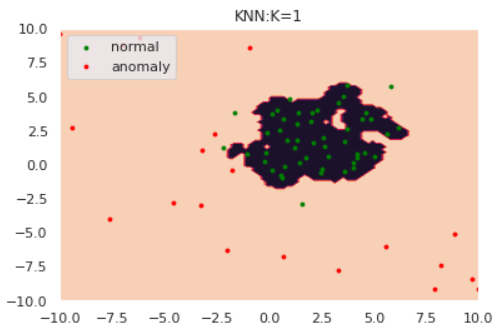
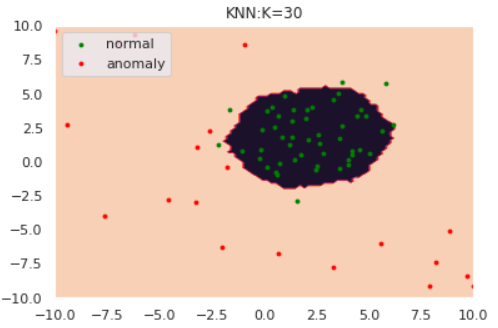
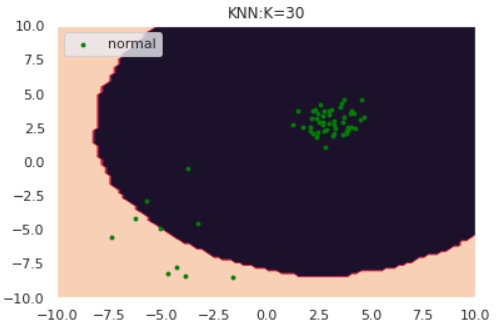
for k in [1,5,30]:
anomaly_scores = kNN(norm, k=k)
thres = pd.Series(anomaly_scores).quantile(0.90)
draw_KNN(norm, anom, thres, k)
kが大きくなるにつれて、正常/異常の境界が滑らかになっていることがわかります。
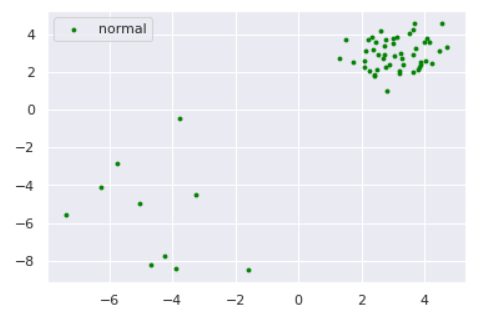
さて、ここで少しいじわるな例で実験してみましょう。以下のように、正常データが密度の違う2つの正規分布から生成されているとします。
np.random.seed(123)
# 平均と分散
mean1 = np.array([3, 3])
mean2 = np.array([-5,-5])
cov1 = np.array([[0.5, 0], [0, 0.5]])
cov2 = np.array([[3, 0], [0, 3]])
# 正常データの生成(2つの正規分布から生成)
norm1 = np.random.multivariate_normal(mean1, cov1, size=50)
norm2 = np.random.multivariate_normal(mean2, cov2, size=10)
norm = np.vstack([norm1, norm2])
s=8
plt.scatter(norm[:,0], norm[:,1], s=s, color='green', label='normal')
plt.legend()
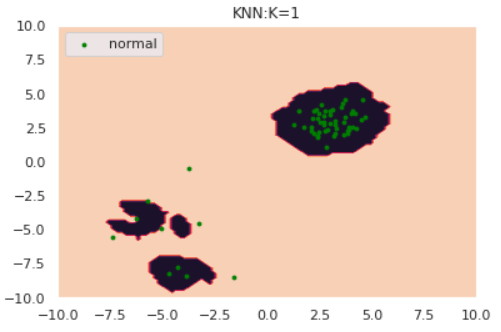
for k in [1,5,30]:
anomaly_scores = kNN(norm, k=k)
thres = pd.Series(anomaly_scores).quantile(0.90)
draw_KNN(norm, [], thres, k, only_norm=True)
特にk=1のケースに注目すると、正常データが密度の異なる別クラスターから発生している場合kNNが上手く動作していないことがわかります。**「密なクラスターからのズレは重要視して、疎なクラスターからのズレは大目に見る」**という処理を加えれば対処できそうだと想像できます。
実はそれが次節で紹介するLOFという手法になります。
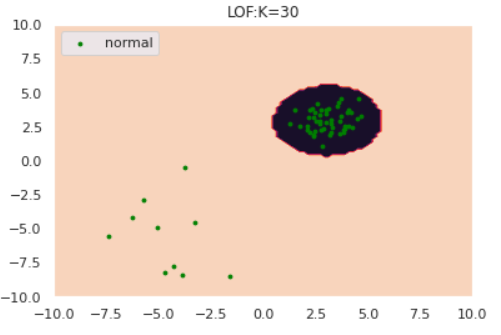
LOF(Local Outlier Factor, 局所外れ値因子法)
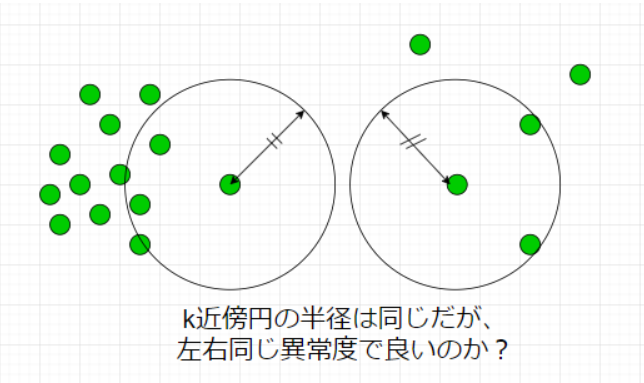
前節で紹介したk-NNが上手く動作しないケースを図で表すと
となります。もちろん、左側の異常度を高くしたいのですが、LOFではデータの密度という概念を導入しそれを実現します。数理的詳細は割愛しますが、以下のようなことをしています。
自身のスカスカ度合いと近傍点のスカスカ度合いの比で異常度を定義しています。
それではLOFの実験を行いましょう。
def draw_LOF(norm, anom, K, only_norm=False):
# plot the line, the points, and the nearest vectors to the plane
xx, yy = np.meshgrid(np.linspace(-10, 10, 100), np.linspace(-10, 10, 100))
Z = - model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = np.array(Z).reshape(xx.shape)
plt.title("LOF:K="+str(K))
plt.contourf(xx, yy, Z)
if not only_norm:
nm = plt.scatter(norm[:, 0], norm[:, 1], c='green', s=s)
am = plt.scatter(anom[:, 0], anom[:, 1], c='red', s=s)
plt.axis('tight')
plt.xlim((-10, 10))
plt.ylim((-10, 10))
plt.legend([nm, am],
["normal", "anomaly"],
loc="upper left",
prop=matplotlib.font_manager.FontProperties(size=11))
if only_norm:
nm = plt.scatter(norm[:, 0], norm[:, 1], c='green', s=s)
plt.axis('tight')
plt.xlim((-10, 10))
plt.ylim((-10, 10))
plt.legend([nm],
["normal"],
loc="upper left",
prop=matplotlib.font_manager.FontProperties(size=11))
plt.show()
from sklearn.neighbors import LocalOutlierFactor
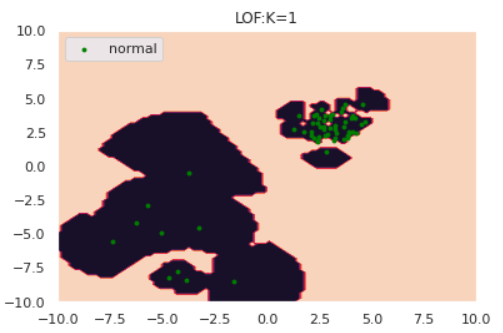
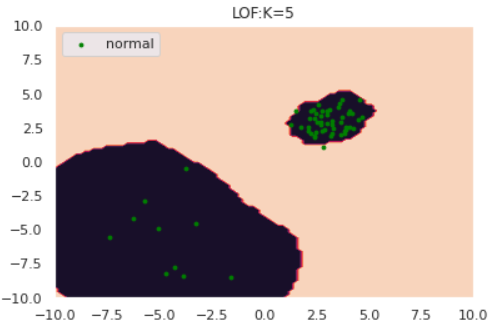
for k in [1, 5, 30]:
model = LocalOutlierFactor(n_neighbors=k, novelty=True)
model.fit(norm)
draw_LOF(norm, [], k, only_norm=True)
このように、クラスターの密度を考慮したうえで異常検知ができていそうです。
発展的な異常検知問題
今後異常検知の勉強をしていくにあたって、以下のようなトピックを勉強してきたいと思っています:
- 時系列データの異常検知
- グラフデータの異常検知
- マネーロンダリング検知に使えそう