この記事について
前回投稿した記事では、マンガでわかる統計学[因子分析編] 第4章の主成分分析のところをPythonで追いかけました。
今回はテキストデータの主成分分析にPythonで挑戦します。
参考
背景・目的
元々、主成分分析を知りたいと思ったきっかけが、この金 明哲氏のテキストアナリティクス本でした。
テキストデータのクラスタリングをやりたいと思っていたところ、この本の主成分分析がおもしろそうだと感じ、これがきっかけで主成分分析を勉強しました。
分析内容について
分析対象は3つのテーマ(友達、車、和食)について書かれた作文データです。
3テーマ × 11人の全部で33件のデータです。
データはこちらのサポートページのソースコードのダウンロードから取得できます。
データは文章ではなく、既にBag of Words(以下、BoW) の形式となっています。
ですので、形態素解析やBoW化するといった処理は今回含まれません。
コード(主成分分析)
コードは前回の記事を流用します。
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
%matplotlib inline
from matplotlib import rcParams
rcParams['font.family'] = 'sans-serif'
rcParams['font.sans-serif'] = ['Hiragino Maru Gothic Pro', 'Yu Gothic', 'Meirio', 'Takao', 'IPAexGothic', 'IPAPGothic', 'Noto Sans CJK JP']
# 作文データの読み込み ※ファイルパスは環境に合わせて修正して下さい。
df = pd.read_csv('./sakubun3f.csv',encoding='cp932')
data = df.values
# "Words"列、"OTHERS"列を除外
d = data[:,1:-1].astype(np.int64)
# データの標準化 ※ 標準偏差は不偏標準偏差で計算
X = (d - d.mean(axis=0)) / d.std(ddof=1,axis=0)
# 相関行列を求めます
XX = np.round(np.dot(X.T,X) / (len(X) - 1), 2)
# 相関行列の固有値、固有値ベクトルを求めます
w, V = np.linalg.eig(XX)
print('------- 固有値 -------')
print(np.round(w,3))
print('')
# 第1主成分を求める
z1 = np.dot(X,V[:,0])
# 第2主成分を求める
z2 = np.dot(X,V[:,1])
##############################################################
# ここまでで求めた第1主成分得点、第2主成分得点をグラフで描画
##############################################################
# グラフ用オブジェクトの生成
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111)
# グリッド線を入れる
ax.grid()
# 描画するデータの境界
lim = [-6.0, 6.0]
ax.set_xlim(lim)
ax.set_ylim(lim)
# 左と下の軸線を真ん中に持っていく
ax.spines['bottom'].set_position(('axes', 0.5))
ax.spines['left'].set_position(('axes', 0.5))
# 右と上の軸線を消す
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
# 軸の目盛の間隔を調整
ticks = np.arange(-6.0, 6.0, 2.0)
ax.set_xticks(ticks)
ax.set_yticks(ticks)
# 軸ラベルの追加、位置の調整
ax.set_xlabel('Z1', fontsize=16)
ax.set_ylabel('Z2', fontsize=16, rotation=0)
ax.xaxis.set_label_coords(1.02, 0.49)
ax.yaxis.set_label_coords(0.5, 1.02)
# データのプロット
for (i,j,k) in zip(z1,z2,data[:,0]):
ax.plot(i,j,'o')
ax.annotate(k, xy=(i, j),fontsize=16)
# 描画
plt.show()
実行結果(主成分分析)
------- 固有値 -------
[ 5.589e+00 4.433e+00 2.739e+00 2.425e+00 2.194e+00 1.950e+00
1.672e+00 1.411e+00 1.227e+00 1.069e+00 9.590e-01 9.240e-01
7.490e-01 6.860e-01 5.820e-01 5.150e-01 4.330e-01 3.840e-01
2.970e-01 2.200e-01 1.620e-01 1.080e-01 8.800e-02 7.800e-02
4.600e-02 3.500e-02 -7.000e-03 -2.000e-03 4.000e-03 1.700e-02
1.300e-02]
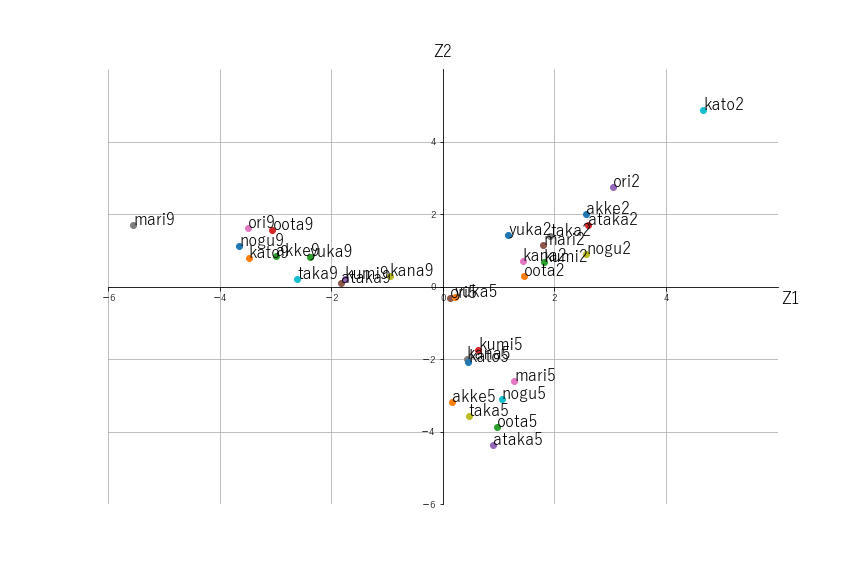
散布図(主成分分析)
結果からの考察
書籍の説明によると、ラベルの末尾が9のテキストは「和食」、末尾が2は「友達」、末尾が5は「車」をテーマにした作文であるとのことです。
書籍とは左右反対に散布図が出力されていますが、左上の方向が「和食」、右上の方向が「友達」、右下の方向が「車」と、3つのテーマがきれいに分類されています。
(書籍と左右反対の図になったのは、固有値の定数倍の任意性によるものかもしれません。)
コード(因子負荷量)
# 最大の固有値に対応する固有ベクトルを横軸、最大から2番目の固有値に対応する固有ベクトルを縦軸とした座標。
V_ = np.array([(V[:,0]),V[:,1]]).T
V_ = np.round(V_,2)
# グラフ描画用のデータ
data_name=df.columns[1:-1]
z1 = V_[:,0]
z2 = V_[:,1]
# グラフ用オブジェクトの生成
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111)
# グリッド線を入れる
ax.grid()
# 描画するデータの境界
lim = [-0.4, 0.4]
ax.set_xlim(lim)
ax.set_ylim(lim)
# 左と下の軸線を真ん中に持っていく
ax.spines['bottom'].set_position(('axes', 0.5))
ax.spines['left'].set_position(('axes', 0.5))
# 右と上の軸線を消す
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
# 軸の目盛の間隔を調整
ticks = np.arange(-0.4, 0.4, 0.2)
ax.set_xticks(ticks)
ax.set_yticks(ticks)
# 軸ラベルの追加、位置の調整
ax.set_xlabel('Z1', fontsize=16)
ax.set_ylabel('Z2', fontsize=16, rotation=0)
ax.xaxis.set_label_coords(1.02, 0.49)
ax.yaxis.set_label_coords(0.5, 1.02)
# データのプロット
for (i,j,k) in zip(z1,z2,data_name):
ax.plot(i,j,'o')
ax.annotate(k, xy=(i, j),fontsize=14)
# 描画
plt.show()
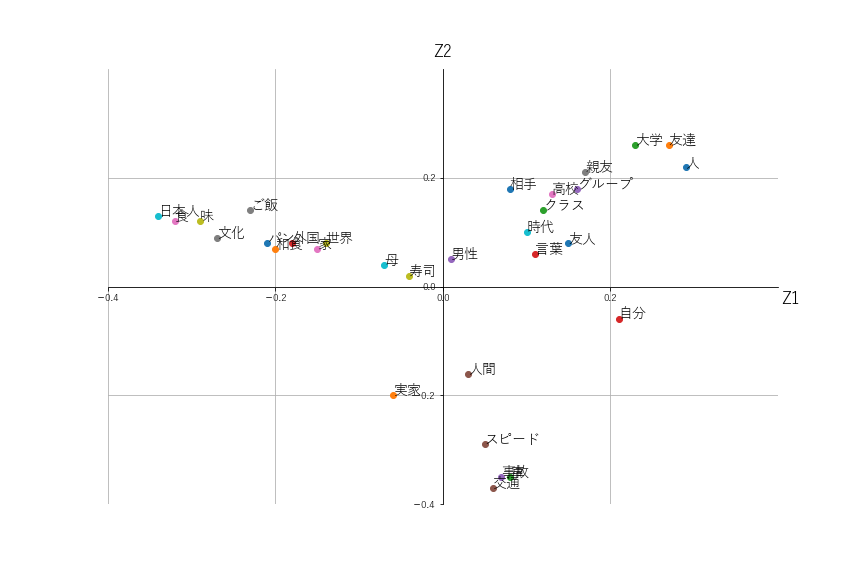
散布図(因子負荷量)
結果からの考察
因子負荷量も左右反対ですが書籍とほぼ同じ結果になりました。
左上の方向に"日本人"、"ごはん"といった「和食」のテーマに関連ありそうな単語が、右上の方向には"親友"、"友人"といった「友達」のテーマに関連ありそうな単語が、右下の方向には"交通"、"事故"といった「車」のテーマに関連ありそうな単語がきています。
主成分の散布図と見比べてみると、それぞれのテーマと関連ありそうな単語の方向が一致していることが分かります。
感想
前回記事のコードを流用してみたところ、思っていたよりも簡単にテキストデータの主成分分析ができました。
今回は既にきれいに前処理されたデータということもあり、きれいな結果が出ました。
次回はニュース記事などできれいに分類できるか確認していきたいと思います。
おわり