Pythonで「マンガでわかる統計学 [因子分析編]」の 第4章 主成分分析 をやってみた

#この記事について
マンガでわかる統計学[因子分析編] 第4章の主成分分析のところをPythonで追いかけてみました。

#参考

• マンガでわかる統計学[因子分析編]

#背景・目的
主成分分析とは何たるかを理解したく、こちらの書籍で勉強しました。

#分析内容について
ラーメン屋さんのレビューデータを主成分分析で分析してみよう！という趣旨の内容です。
レビュー項目は、「麺」、「具」、「スープ」の3項目です。
主成分分析を行うことで、総合評価No.1の店舗はどこか？、総合評価に最も影響を及ぼす項目が何か？が分かります。

データ

店名	麺	具	スープ
二楽	2	4	5
夢田屋	1	5	1
地回	5	3	4
なのはな	2	2	3
花ぶし	3	5	5
昇辰軒	4	3	2
丸蔵らあめん	4	4	3
海楽亭	1	2	1
なるみ家	3	3	2
奏月	5	5	3

コード（主成分分析）

以下のコードでは、主成分得点の算出から第1主成分と第2主成分の二次元で点グラフを描画するまでをやっています。

import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
from matplotlib import rcParams
rcParams['font.family'] = 'sans-serif'
rcParams['font.sans-serif'] = ['Hiragino Maru Gothic Pro', 'Yu Gothic', 'Meirio', 'Takao', 'IPAexGothic', 'IPAPGothic', 'Noto Sans CJK JP']

# ラーメン屋レビューデータ
data = np.array([
    ['二楽',2,4,5],
    ['夢田屋',1,5,1],
    ['地回',5,3,4],
    ['なのはな',2,2,3],
    ['花ぶし',3,5,5],
    ['昇辰軒',4,3,2],
    ['丸蔵らあめん',4,4,3],
    ['海楽亭',1,2,1],
    ['なるみ家',3,3,2],
    ['奏月',5,5,3],
])

print('------- 元データ -------')
print(data)
print('')

# 型変換
d = data[:,1:].astype(np.int64)

# データの標準化 ※ 標準偏差は不偏標準偏差で計算
X_ = np.round((d - d.mean(axis=0)) / d.std(ddof=1,axis=0),1)
print('------- 標準化後のデータ -------')
print(X_)
print('')

# 標準化する時点で四捨五入してしまうと、
# この次の相関行列の値が合わなくなるので計算し直しています
X = (d - d.mean(axis=0)) / d.std(ddof=1,axis=0)

# 相関行列を求めます
XX = np.round(np.dot(X.T,X) / (len(X) - 1), 2)

print('------- 相関行列 -------')
print(XX)
print('')

# 相関行列の固有値、固有値ベクトルを求めます
w, V = np.linalg.eig(XX)

print('------- 固有値 -------')
print(np.round(w,1))
print('')
print('------- 固有ベクトル -------')
print(np.round(V,2)) # 1番目の固有値が書籍と一致しないのは、固有ベクトルの定数倍の任意性によるものらしい…
print('')

# 第1主成分を求める
# ※ 末尾の -1 かけているのは、書籍の結果と合わせるための処置。
#    符号を反転させても定数倍の大きさは変化ないため問題ないと思う…
z1 = np.round(np.dot(X,V[:,0]),1) * -1
print('------- 第1主成分 -------')
print(z1)
print('')

# 第2主成分を求める
z2 = np.round(np.dot(X,V[:,1]),1)
print('------- 第2主成分 -------')
print(z2)
print('')

##############################################################
# ここまでで求めた第1主成分得点、第2主成分得点をグラフで描画
##############################################################

# グラフ用オブジェクトの生成
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111)

# グリッド線を入れる
ax.grid()

# 描画するデータの境界
lim = [-2.5, 2.5]
ax.set_xlim(lim)
ax.set_ylim(lim)

# 左と下の軸線を真ん中に持っていく
ax.spines['bottom'].set_position(('axes', 0.5))
ax.spines['left'].set_position(('axes', 0.5))
# 右と上の軸線を消す
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)

# 軸の目盛の間隔を調整
ticks = np.arange(-2.5, 2.5, 0.5)
ax.set_xticks(ticks)
ax.set_yticks(ticks)

# 軸ラベルの追加、位置の調整
ax.set_xlabel('Z1', fontsize=16)
ax.set_ylabel('Z2', fontsize=16, rotation=0)
ax.xaxis.set_label_coords(1.02, 0.49)
ax.yaxis.set_label_coords(0.5, 1.02)

# データのプロット
for (i,j,k) in zip(z1,z2,data[:,0]):
    ax.plot(i,j,'o')
    ax.annotate(k, xy=(i, j),fontsize=16)

# 描画
plt.show()

実行結果（主成分分析）

------- 元データ -------
[['二楽' '2' '4' '5']
 ['夢田屋' '1' '5' '1']
 ['地回' '5' '3' '4']
 ['なのはな' '2' '2' '3']
 ['花ぶし' '3' '5' '5']
 ['昇辰軒' '4' '3' '2']
 ['丸蔵らあめん' '4' '4' '3']
 ['海楽亭' '1' '2' '1']
 ['なるみ家' '3' '3' '2']
 ['奏月' '5' '5' '3']]

------- 標準化後のデータ -------
[[-0.7  0.3  1.4]
 [-1.3  1.2 -1.3]
 [ 1.3 -0.5  0.8]
 [-0.7 -1.4  0.1]
 [ 0.   1.2  1.4]
 [ 0.7 -0.5 -0.6]
 [ 0.7  0.3  0.1]
 [-1.3 -1.4 -1.3]
 [ 0.  -0.5 -0.6]
 [ 1.3  1.2  0.1]]

------- 相関行列 -------
[[1.   0.19 0.36]
 [0.19 1.   0.3 ]
 [0.36 0.3  1.  ]]

------- 固有値 -------
[1.6 0.8 0.6]

------- 固有ベクトル -------
[[-0.57 -0.6  -0.56]
 [-0.52  0.79 -0.32]
 [-0.63 -0.11  0.77]]

------- 第1主成分 -------
[ 0.7 -1.   1.  -1.1  1.5 -0.3  0.6 -2.3 -0.7  1.4]

------- 第2主成分 -------
[ 0.5  1.9 -1.3 -0.7  0.8 -0.7 -0.1 -0.1 -0.3  0.1]

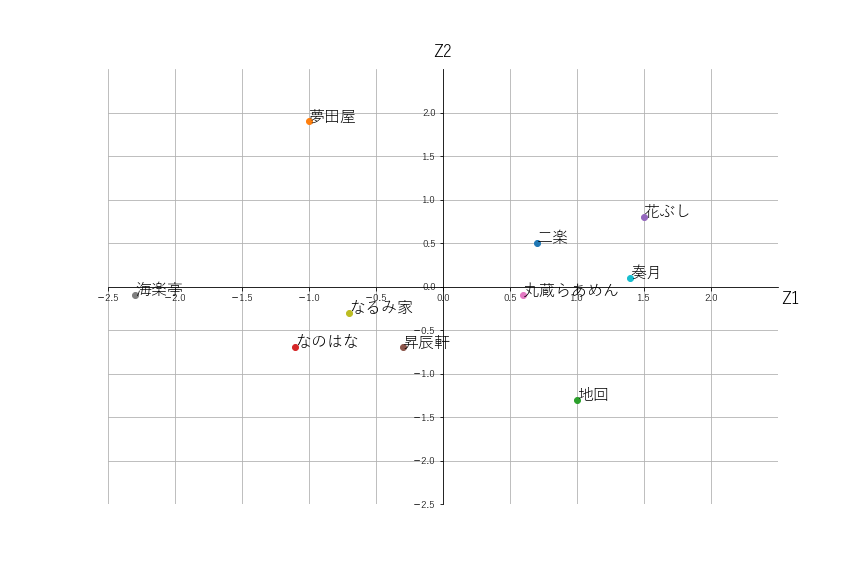
#点グラフ（主成分分析）

#結果からの考察
第1主成分に対応するのはZ1軸、第2主成分に対応するのはZ2軸です。
真ん中の原点からZ1軸の正方向に1番離れているのは「花ぶし」です。その次が「奏月」です。
このことから、総合評価No.1は「花ぶし」、No.2は「奏月」であることが分かります。

では、総合評価に影響を及ぼした項目な何でしょうか？
これは求めた固有ベクトルを点グラフで描画することで見えてきます。

#コード（影響を及ぼした項目）

# 最大の固有値に対応する固有ベクトルを横軸、最大から2番目の固有値に対応する固有ベクトルを縦軸とした座標。
V_ = np.array([(V[:,0] * -1),V[:,1]]).T
V_ = np.round(V_,2)
print('------- 座標 -------')
print(V_)
print('')

# グラフ描画用のデータ
data_name=['麺','具','スープ']
z1 = V_[:,0]
z2 = V_[:,1]

# グラフ用オブジェクトの生成
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111)

# グリッド線を入れる
ax.grid()

# 描画するデータの境界
lim = [-1.0, 1.0]
ax.set_xlim(lim)
ax.set_ylim(lim)

# 左と下の軸線を真ん中に持っていく
ax.spines['bottom'].set_position(('axes', 0.5))
ax.spines['left'].set_position(('axes', 0.5))
# 右と上の軸線を消す
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)

# 軸の目盛の間隔を調整
ticks = np.arange(-1.0, 1.0, 0.2)
ax.set_xticks(ticks)
ax.set_yticks(ticks)

# 軸ラベルの追加、位置の調整
ax.set_xlabel('Z1', fontsize=16)
ax.set_ylabel('Z2', fontsize=16, rotation=0)
ax.xaxis.set_label_coords(1.02, 0.49)
ax.yaxis.set_label_coords(0.5, 1.02)

# データのプロット
for (i,j,k) in zip(z1,z2,data_name):
    ax.plot(i,j,'o')
    ax.annotate(k, xy=(i, j),fontsize=16)
    
# 描画
plt.show()

実行結果（影響を及ぼした項目）

------- 座標 -------
[[ 0.57 -0.6 ]
 [ 0.52  0.79]
 [ 0.63 -0.11]]

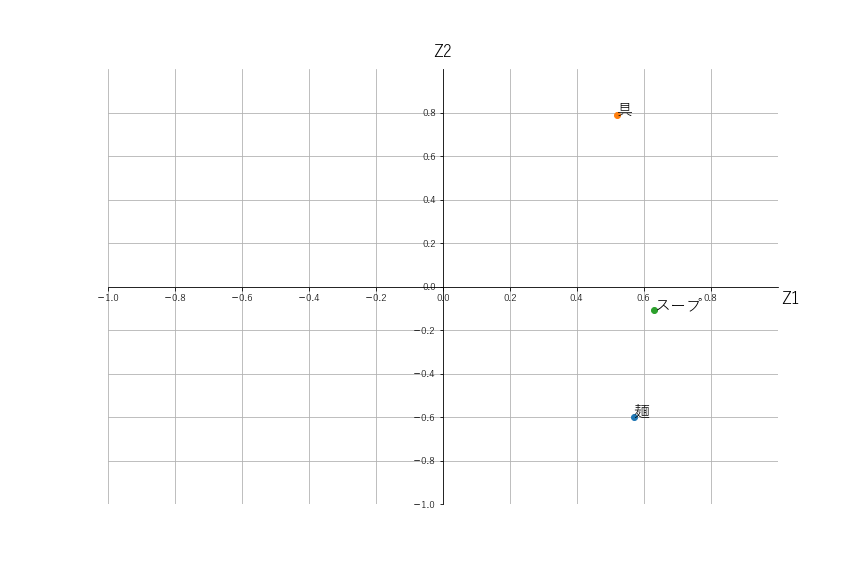
#点グラフ（主成分分析）

#総合評価に影響を及ぼした項目
固有ベクトルを点グラフで描画した結果を見ると、Z1軸の正方向に1番大きい値なのは「スープ」です。
続いて「麺」、「具」です。
このことから、ラーメンの総合評価に最も影響を与える項目は「スープ」であることが分かります。

その他結果から見えてくるもの

あらためて主成分分析の点グラフと固有ベクトルの点グラフを並べてみます。


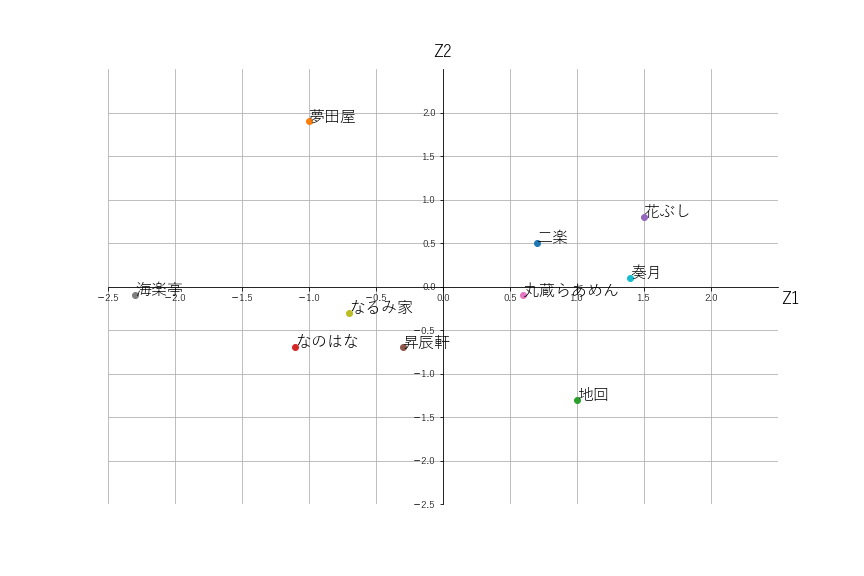
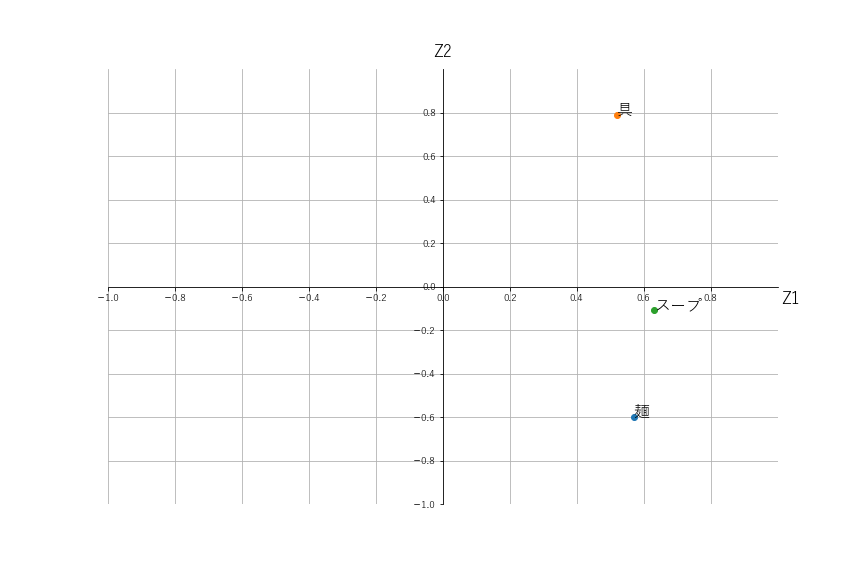
固有ベクトルの点グラフでは、Z2軸の正方向に「具」の項目が、負方向には「麺」が来ています。
主成分分析の点グラフでは、Z2軸の正方向に1番大きい値なのは「夢田屋」で、負方向に1番大きいのは「地回」です。

このことから、「夢田屋」は「具」が評価されているラーメン屋さんであり、「地回」は「麺」が評価されているラーメン屋さんであることが分かります。

元データを確認してみると、確かに「夢田屋」は「具」の評価点が5点であり、「地回」は「麺」の評価点が5点です。

#感想
ラーメン屋さんのレビューデータから総合評価No.1を見つけるというおもしろい切り口で、楽しく主成分分析の概要を知れたように思いました。

おわり