2点間の距離が1以下という条件の下で,面積が最大となる$n$角形を考えてみてください.
$n=3$の場合,その答えは正三角形です.
$n=4$の場合,その答えは正方形です.ただし,正方形以外にも答えが無数にあります.
$n=5$の場合,その答えは正五角形です.
$n=6$の場合,その答えは正六角形ではありません.答えは Graham's Biggest Little Hexagon(グラハムの最大の小さな六角形)と呼ばれる,以下の図形です.
 |
 |
|---|---|
| 正六角形 | Graham's Biggest Little Hexagon |
 |
 |
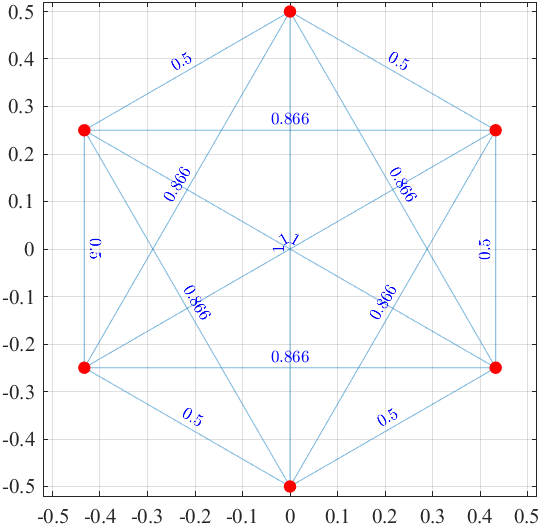
| 正六角形 (2点間の距離を記載) |
Graham's Biggest Little Hexagon (2点間の距離を記載) |
正六角形の面積$=\frac{3}{8}\sqrt{3}=0.649519...$です.
一方,Graham's Biggest Little Hexagon の面積$=0.674981...$です.
すなわち,Graham's Biggest Little Hexagon は,正六角形より面積が3.92%大きいです.
非常に興味深いですよね.$n$が7以上の場合は,どうなるのでしょうか.
この記事では,2点間の距離が1以下で面積が最大となる多角形 LSPを紹介します.
プログラム,画像,点群データを以下に公開しています.言語はMATLABです.
また,プログラムについては,以下の記事で紹介しています.
2点間の距離が1以下で面積が最大となる多角形 LSP
「2点間の距離が1以下で面積が最大となる多角形」は,英語では Biggest little polygon,Largest Small Polygon (LSP),Largest Small $n$-polygons などと表現されています.
wikipediaの記載は Biggest little polygon ですが,この記事では主要な論文に準拠し,「2点間の距離が1以下で面積が最大となる多角形」のことをLSPと表記します.
正三角形はLSP(3),Graham's Biggest Little HexagonはLSP(6),面積最大の$n$角形はLSP($n$)です.
LSPは,「直径が1以下で面積が最大となる多角形」のような表現をされることがあります.
ここでいう直径は,図の直径や多角形の直径という意味で,直径を円や球以外にも拡張した概念である点に注意が必要です.
LSP(n): nが奇数の場合
$n=$奇数の場合,LSP($n$)は正多角形,正$n$角形になります.
$n=3,5,7,9$における図形は,以下の通りです.
 |
 |
|---|---|
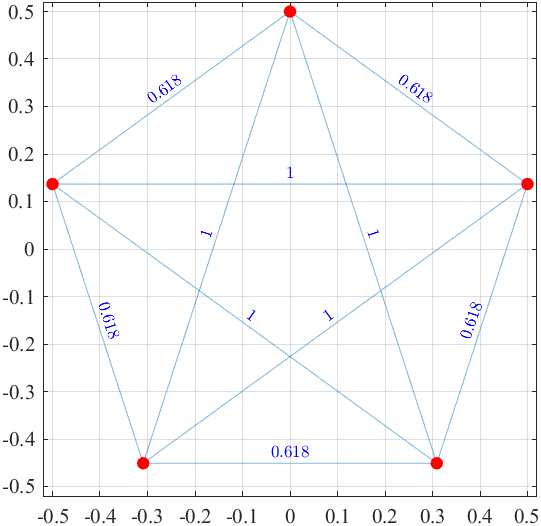
| LSP(3):正三角形,面積:0.433012... | LSP(5):正五角形,面積:0.657163... |
 |
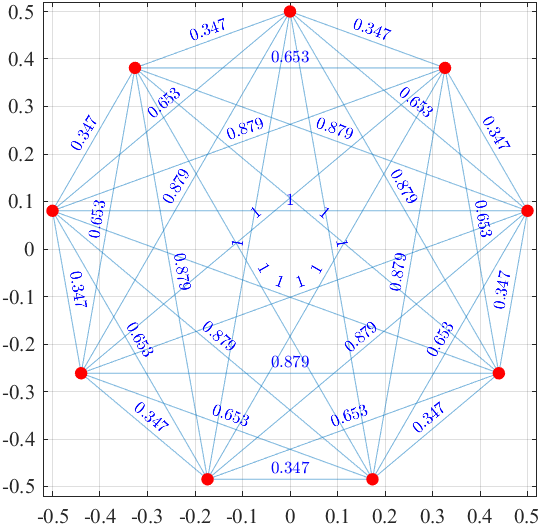 |
| LSP(7):正七角形,面積:0.719740... | LSP(9):正九角形,面積:0.745619... |
以下の論文で,$n=$奇数の場合にLSP($n$)が正$n$角形になることが証明されています.
- Reinhardt, K. (1922), "Extremale Polygone gegebenen Durchmessers", Jahresbericht der Deutschen Mathematiker-Vereinigung, 31: 251–270.
LSP(4): 面積=0.5の midsquare quadrilaterals
LSP(4)は,無限に存在します.
具体的には,面積=0.5のmidsquare quadrilateralsは,すべてLSP(4)になります.
midsquare quadrilateralsとは,以下の条件を満たす四角形です.
- Equidiagonal quadrilateral(2つの対角線の長さが等しい凸四角形)である
- 直交対角線四角形(対角線が直交する四角形)である
要するに,対角線の長さが1で,対角線が直角に交わり,2つの対角線の長さが等しく,凸な(凹でない)四角形がLSP(4)になります.
以下に具体例を4つほど示します.面積はいずれも$\frac{1}{2}\times1\times1=0.5$になります.
 |
 |
|---|---|
| LSP(4):正方形 | LSP(4):凧形 |
 |
 |
| LSP(4):台形 かつ 直交対角線四角形 | 直交対角線四角形 |
LSP(6): Graham's Biggest Little Hexagon
LSP(6)は,Graham's Biggest Little Hexagonという名前がついています.
冒頭で述べた通り,正六角形は,LSP(6)ではありません.以下の図を見てみましょう.
 |
 |
|---|---|
| 正六角形,面積:0.649519... | LSP(6),面積:0.674981... |
図形の頂点に番号を記載し,長さ1の線を黒色にしました.
長さ1の線が正六角形は3本しかないのに対し,LSP(6)は6本あることが確認できます.
2つの図形は,頂点1,4は同じ位置にありますが,その他の4点の位置が異なります.
正六角形と比較して,LSP(6)の頂点3,5は,頂点1から最大限遠い位置に移動しています.
また,頂点2,6は,左右に目一杯離れた位置で,頂点3,5とも離れた位置に移動しています.
このような点の移動によって,六角形の面積が増加したことが確認できました.
ところで,LSP(6)から頂点4を削除した五角形は,正五角形とどう違うのか検証してみます.
下の図(左)はLSP(6)から作成した五角形,(右)はその五角形と正五角形を重ねたものです.
 |
 |
|---|---|
| 五角形,面積:0.654029... | 五角形と正五角形(黒) |
五角形の面積は0.654029...であり,正五角形の面積0.657163...より0.477%ほど小さいです.
五角形の周の長さは3.089067...であり,正五角形の周の長さ3.090169...より僅かに小さいです.
LSP(6)内に現れる五角形は,正五角形から正三角形に変化する途中の図形であり,正五角形を僅かに崩した図形だと確認できます.
こちらのブログに公開されているgifが視覚的にわかりやすいです.
LSP(n): nが偶数の場合
LSP(8)とLSP(10)も,正八角形や正十角形とは異なります.以下のような図になります.
 |
 |
|---|---|
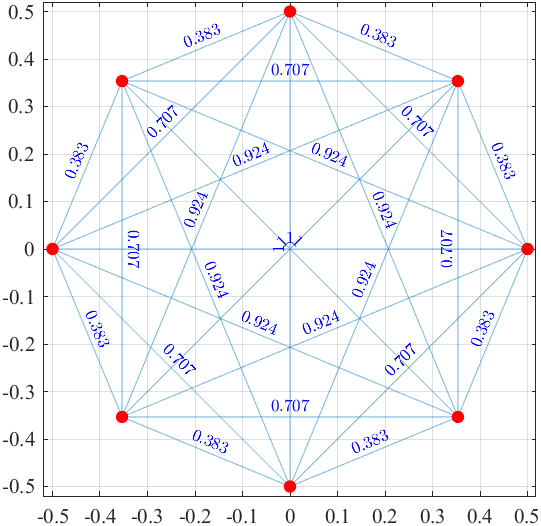
| 正八角形,面積:0.707106... | LSP(8),面積:0.726868... |
 |
 |
| 正十角形,面積:0.734731... | LSP(10),面積:0.749137... |
LSP(8),LSP(10)共に,頂点$(0,0.5)$からの距離が1の頂点が3つ存在し,正$n$角形より面積が大きいことが確認できます.
$n$が大きくなるにつれて,生成される図形は円に近づき,正$n$角形とLSP($n$)の差も小さくなっていきます.
LSP($n$)の$n\geq10$については,以下の論文が参考になります.
- Pint'er, J.D., Kampas, F.J., & Castillo, I. (2021). "Finding the Sequence of Largest Small n-Polygons by Numerical Optimization", arXiv:2101.01263 [math.OC].
LSPの歴史と補足(勘違いの可能性あり)
$n=$奇数の場合,LSP($n$)は正多角形,正$n$角形になるということは,今から100年以上前に証明されています.そして,LSP(6)については,1956年にHanfried Lenzが問題提起し,1975年にRonald Grahamが解を発表しました.
論文によると,以下の10次元方程式の解$A$がLSP(6)の面積になります.
$4096A^{10}+8192A^9-3008A^8-30848A^7+21056A^6+146496A^5$
$-221360A^4+1232A^3+144464A^2-78488A+11993=0$
- Graham, R. L. (1975), "The largest small hexagon", Journal of Combinatorial Theory, Series A, 18 (2): 165–170.
このグラハム博士,1986年に来日されていたみたいで,グラハム博士中学生に語る-数学はわくわくするほど面白い-という日本語資料が残されています.
講演では,タタミ敷きつめ問題,ルービックキューブ,巡回セールスマン問題に続いて,多角形問題としてLSPを取り上げています.
この時点では,LSP(8)の完全な解に対して250ドルの賞金が掛けられていたようです.
方程式を導出することが完全な解だとすると,今現在もLSP(8)は完全解決していないと思われます.
幾つかの論文を軽く見たのですが,論文内では,精度の高いLSP(8)近似解の導出,あるいはLSP(8)に関する上界・下界の証明をしていました.
LSP(8)の条件を列挙できても,$x$次元方程式に落とし込めていないように見受けられました.
以下の論文等から情報を辿って,ファクトチェックをお願いいたします.
- Audet, C., Hansen, P., Messine, F., Xiong, J. (2002), "The largest small octagon", Journal of Combinatorial Theory, Series A, 98 (1): 46–59.
- Foster, J., Szabo, T., (2007), "Diameter graphs of polygons and the proof of a conjecture of Graham", Journal of Combinatorial Theory, Series A, 114 (8): 1515–1525.
終わりに
Largest Small Polygon (LSP) を紹介しました.
日本語資料が少ないので理解に苦労しましたが,その分,良い記事ができたと思います.
工学の博士である自分には疎い部分があるので,数学の得意な皆様にLSP(8)の完全な解について確認をお願いしたいところです.本当に賞金が掛けられているのでしょうか?
本記事の執筆に利用したプログラム,画像,点群データは,以下に公開しています.
このプログラムの内容を紹介した以下の記事も併せてご確認ください.
