M5StickCの内蔵マイクを使って騒音計を作るのはなかなか難しい。マイクからの入力を既知の単位、例えばdB(デシベル)に変換する方法が自明ではなく、実際に実装してみたというサンプルもあまり見ない。そこで遊び半分に次のようなブートストラッピングを試してみたところ、意外とちゃんとした数値が出るようになったので紹介してみることにする。
- とにかく音圧またはパワーを(単位不明でよいので)数値化して表示するアプリ(初期騒音計)を作る。
- それをスマフォのdB表示騒音計と並べて比較して対応を取り、変換式を検討する。
- その変換式を用いて初期騒音計をdB表示騒音計にアップグレードする。
完成品の動作の様子:
完成品のソースコード:
ステップ1: 初期騒音計の作成
スケッチ例 "Microphone" を用いたサンプリング
M5StickCのマイクと言えばみなさんおなじみ、入力波形を表示するスケッチ例 Microphone があるので、これを取っ掛かりとする。
ただしこのスケッチ例はサンプリングレート44.1kHz、一回のサンプル数が256であり、今回の目的には適切でない気がする。音圧や音のパワーを測るのにこのサンプリングレートは高すぎるし、一回のサンプリング時間が256/44100=0.0058秒というのはあまりにも短いように思える。そこでもう少し適切な値を選んでみる。
では、騒音の計測において拾うべき周波数帯を調べてみよう。参考文献「環境騒音の周波数分析について - 山梨県」のチャートを眺めてみると、主に数百Hzあたりを見ればよく、セミの声を拾いたければ数kHzを見る必要がありそうだ。これなら直感的にはかなり低いサンプリングレートでも問題なさそうだが、あまりケチる動機もないので、せっかくなのでセミの声にも対応できそうなサンプリングレート16kHz、一回のサンプル数512くらいにしてみよう。これでナイキスト周波数8kHz、一回のサンプリング時間512/16000=0.032秒=31.25Hz相当となり、まぁそんなものでよかろうという気になる。M5StickCのマイクSPM1423のデータシートに載っている周波数応答(100Hz~10kHz)に照らしても、まぁそんなものだろう。
データ処理
スケッチ例 Microphone にはサンプリングデータが溜まるたびに呼ばれる showSignal 関数があり、ここに波形を(かなり雑に)表示する処理が実装されている。これを転用して騒音計算用のデータ処理を実装する。なおオリジナルのコードにはshowSignalの後に余計な100msのディレイが入っているので、これは抜いてyieldなり短いdelayなりで処理しておくこと。
バイアス補正
マイクからのデータは符号付き16ビット(精度は12ビット)だが、ゼロが正確にゼロではなく、バイアス(直流成分)が含まれる。これが「騒音」を測定するユースケースで問題になるとはあまり思えないが、静寂がきちんと静寂と見える方がテンション上がるので補正を試みる。
補正方法はサンプルの平均を取ってそれをバイアスと見做すだけだが、データの変化でいちいちブレるのも困るので、みんな大好きローパスフィルタ(正式にはIIRフィルタと言うのかな?)をかけることにする。
y_i = \alpha y_{i-1} + (1-\alpha)x_i
αはなるべく大きい値が望ましいが、大きすぎると収束に時間がかかるので、起動後10秒程度で収束しそうな0.98とした。
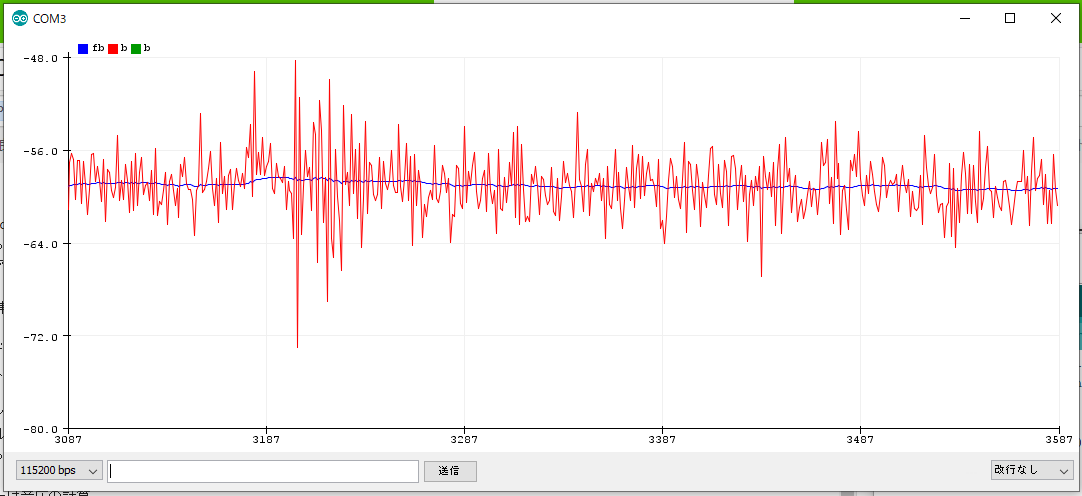
下のチャートはバイアス値のプロット例である(赤=フィルタ前、青=フィルタ後)。バイアス値はM5StickCの個体によって異なるが、-60や-80といった値が観測された。音が入力されると生の平均値(赤)は大きく揺れるが、フィルタをかけた値(青)は十分安定している。
パワーまたは音圧の計算
波のサンプルからパワーを求めるには二乗平均が適当だろう、ということでとりあえずバイアス補正後の値の二乗平均を取ってみる。(ちなみになぜ二乗平均なのか、この参考文献「2乗平均値や実効値が使われる理由」に親切な説明があったので理解したい人は一読するとよいだろう。) 計算結果を二乗平均のままにする(=パワーを得る)か、それとも平方根を取る(=音圧を得る)かはどちらでもよい。dBに変換する際にはどこかで対数を取ることになり、そのときに係数に吸収されてしまうからだ。ただ、二乗のままだと桁数の変動が大きすぎて読みにくかったので、純粋に人間様の読みやすさ都合により平方根を取ることにした。
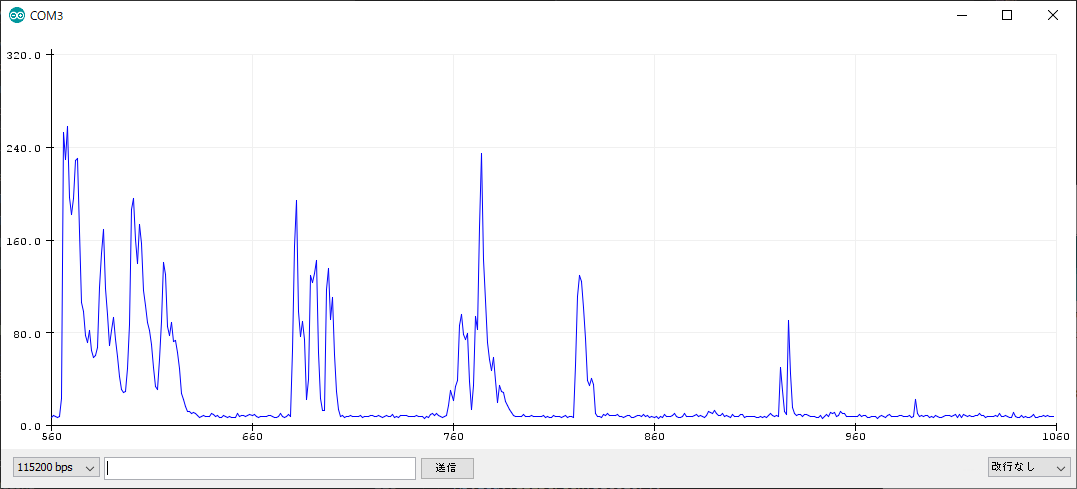
下のチャートは上の計算で得られた値のプロット例である。声を出したときには息の強弱にも敏感に反応し、単位が謎であることを除き(笑)、かなりいい感じである。
平滑化
初期騒音計の目的はスマフォの騒音計アプリとの対応を見ることなので、あまり敏感に値がころころ変わるよりは、ある程度一定の音を聞かせることを前提として鈍感な出力を出してくれる方が読みやすい。というわけで、1秒ごとに平均値を求めて出力値とする。この時点で、1秒ごとに単位不明の値を表示する「なんちゃって騒音計」の完成である。
ステップ2: スマフォの騒音計アプリとの対応付け
スマフォの騒音計アプリと並べて様々な大きさの音を聞かせ、値を比較してみる。あまり厳密にやるのも疲れるので、声を出す・部屋や時間を変える・窓を開閉する・ものの音を聞かせる(換気扇・ガレージドアの開閉・PCのファン・生ギター)など、遊びと割り切って気軽にやってみた。
| 初期騒音計出力 | スマフォ騒音計出力(db) | 備考 |
|---|---|---|
| 8 | 30 | 静かな部屋 |
| 13 | 40 | PCのファン |
| 30 | 50 | 小声でしゃべる(40cmの距離) |
| 65 | 60 | 普通にしゃべる(同上) |
| 160 | 70 | 大き目の声でしゃべる(同上) |
| 500 | 80 | 近くで大声を出す、生ギターを弾く |
| 900 | 85 | 換気扇の真下 |
| 1500~ | 90 | 近くで頑張って大声を出す |
これを試しにExcelに入れて対数近似曲線を描かせてみたら…なんと予想外のフィットぶり!
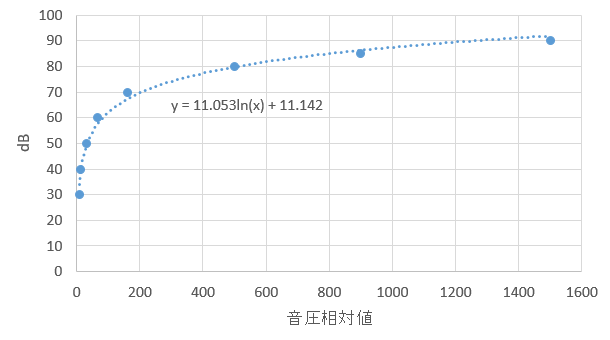
つまりExcel様のはじき出したこれが、謎の音圧値をdBに(およそ)変換してくれる魔法の式ということである:
y = 11.053 \; log_e(x) + 11.142
ステップ3: 初期騒音計のアップグレード
変換式さえわかってしまえば、その式を適用してこれがdB値だと言い張るだけで、謎の騒音計がdB表示騒音計に早変わりである。まったく簡単だ。出来栄えは冒頭の動画の通りである。
最終的な可視化方法は自分の用途や好みによって定めることが望ましい。私は最終的に0.5秒ごとの平均値を表示し、騒音レベルによって色を変えたりLEDを光らせるようにしたが、平滑化せずに生のデータをチャート表示したい・平均値ではなく最大値を表示したい・表示間隔をもっと短く/長くしたい、といった要件はあり得るだろう。
おまけ: 理論的変換式の導出
これで実用的には満足いくものができてしまったが、理論的理解を深めるためマイクSPM1423のデータシートから変換式を導出して「答え合わせ」をしてみようと思う。
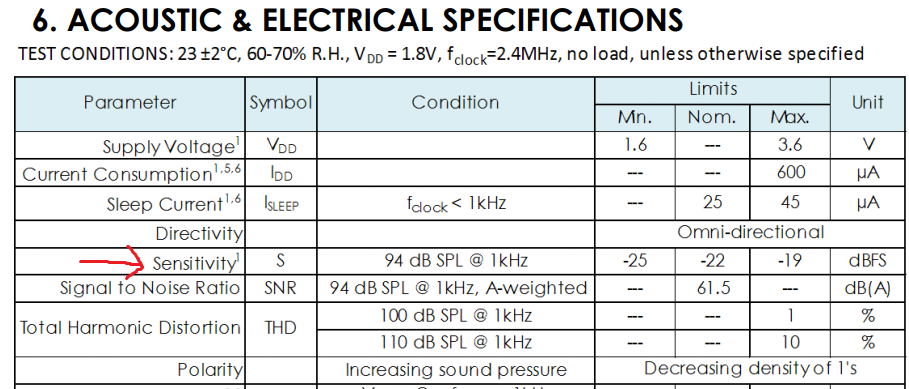
データシートの中でポイントとなる値は感度 Sensitivity であるが、条件が 94 dB SPL @ 1kHz、値が -22 dBFS (許容誤差±3)と書いてある。意味が解らない。(´・ω・`)ショボーン
そこで資料を探したところ、この "Understanding Microphone Sensitivity" というのを読んでやっと理解できるようになった。
つまり、このデジタルマイクに94dB=1Paの音圧の1kHzの音を加えると、フルスケールに対して-22dBの倍率の値を出力しますよ、ということである。このマイクの出力は16ビットなのでフルスケールは±32768、デシベル計算機を使って-22dBを倍率に変換すると0.07943、つまりこの条件でのマイク出力値はざっくり±2603になるということだ。マイク出力が線形であるなら、出力値を2603で割ればPaで表した音圧を得ることができるということである。本当か?まあいい。そういうことにして話を進める。
音圧がPaでわかればdBも公式から計算できるので、$ x $をマイク出力値とすればこうなる。
\begin{align}
p \; [Pa] &= \frac{x}{2603} \\
y \; [dB] &= 20 \; log_{10} (\frac{p}{2.0 \times 10^-5}) \\
&= 8.6859 \; log_e(x) + 25.6699
\end{align}
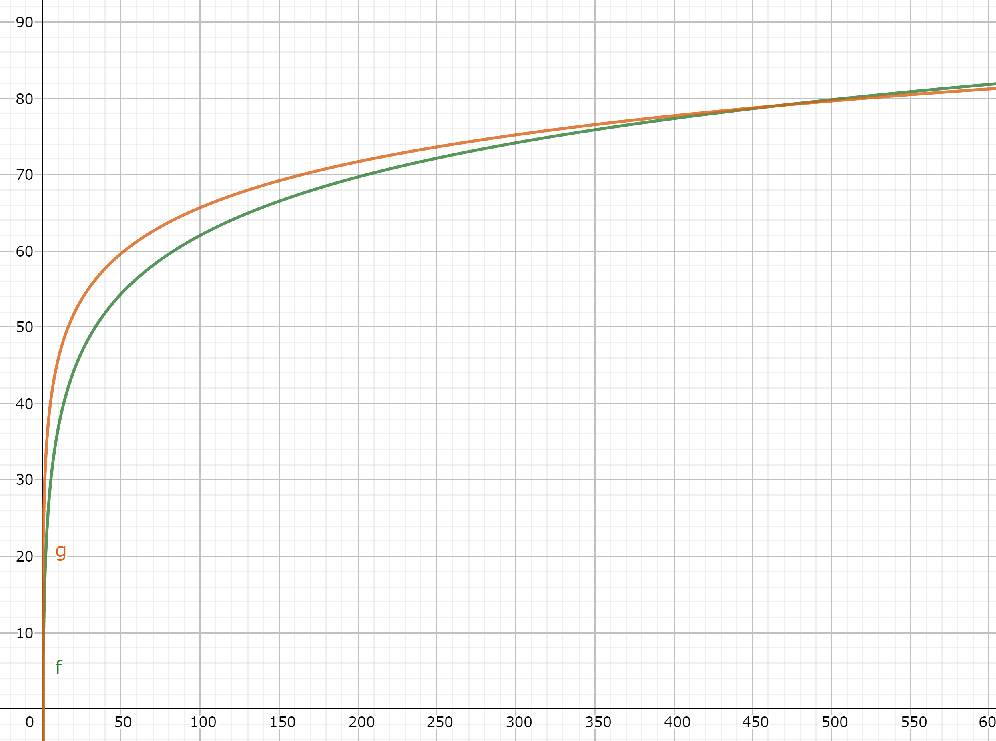
これをチャートにプロットしてみると下記のようになる。緑がスマフォアプリを参照してExcelで求めた実測近似式、オレンジが上の計算で求めた理論式である。うむ、なかなかいい線いっているではないか。ただ理論式は静かな領域で近似式よりも大きな値が出てしまい、これが各自治体の発行しているデシベルの目安に対して確かに大きすぎると思えるので、このまま実測近似式の方を採用しておくことにする。
以上です。(・∀・)