この記事は Lancers(ランサーズ) Advent Calendar 2022 の13日目の記事です。昨日の記事は @narinarinari さんによる「アドラー心理学」を用いたチームマネジメントでした。
トピックモデル
トピックモデルとは文書が潜在的なトピックから生成されると仮定し、それをモデリングしたものです。トピックモデルを活用することで、ある文書が持つ潜在的なトピックやその分布を推定したり、教師なしで文書分類を行えたり、同じトピックにはどのような単語が含まれやすいかを分析することなどができます。本記事ではこのトピックモデルの1つである Latent Dirichlet Allocation (LDA)を実際にランサーズのテキストデータに対して適用してどのような結果になるか見ていきます。
Latent Dirichlet Allocation
簡単に LDA について説明します。LDA のグラフィカルモデルを以下の図に示します。
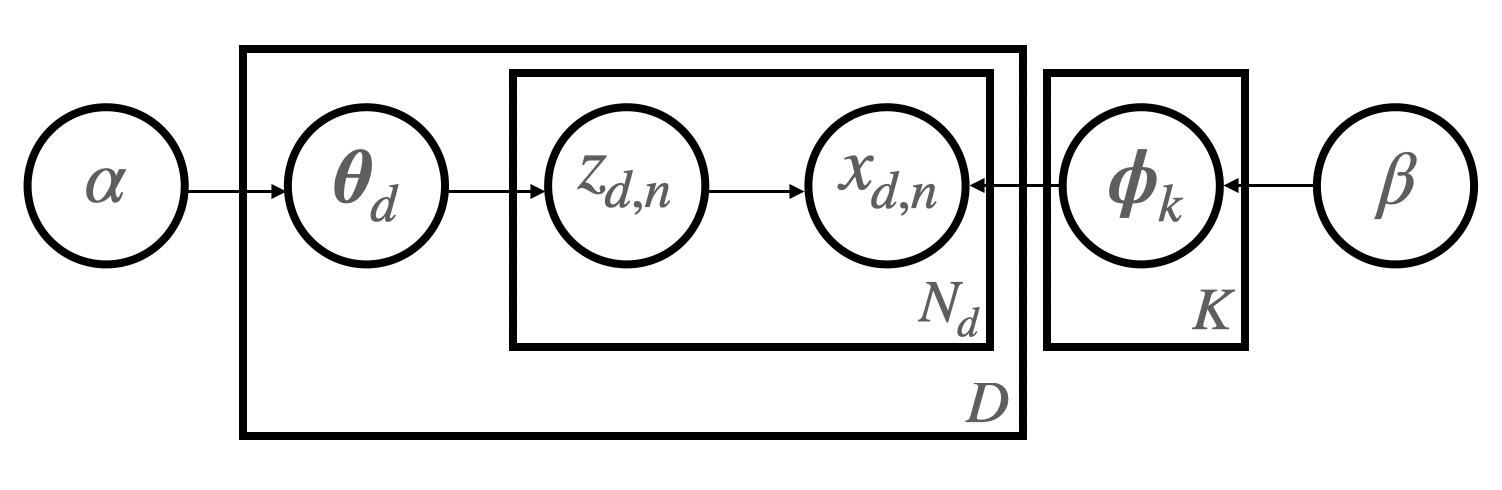
この生成過程では、現実世界には複数のトピックがあり、1つの文書は複数のトピックから構成されていると仮定します。例えば同じ文書内で政治や経済、スポーツなどについて触れられていることもあり、それらのトピックが混ざって文書が作られていると考えます。さらに各トピックごとに生成されやすい単語は異なると考えるのが自然です。スポーツに関するトピックならば「ホームラン」や「得点」などの単語が出てきやすいが、政治のトピックならばそれらが出現する確率は小さいなどです。この生成モデルでは、文書は大量にあるがそのトピックが明示的に与えられていないときに、各文書のトピックを推定したり、あるトピックからはどのような単語が生成されやすいかを学習することができます。
詳しい生成過程を見ていきましょう。まず、$k \in \lbrace 1, ..., K \rbrace$ 番目のトピックが持つ単語分布が生成されます。
\boldsymbol{\phi}_k = [\phi_{k, 1}, ..., \phi_{k, V}]^\mathsf{T} \sim \text{Dirichlet}(\beta).
ここで $V$ は語彙サイズを表します。また $d \in \lbrace 1, 2, ..., D \rbrace$ 番目の文書が持つトピック分布も同様に生成されます。
\boldsymbol{\theta}_d = [\theta_{d, 1}, ..., \theta_{d, K}]^\mathsf{T} \sim \text{Dirichlet}(\alpha) .
最後に $d$ 番目の文書の $n \in \lbrace 1, ..., N_d \rbrace$ 番目の単語 $x_{d, n} \in \lbrace 1, ..., V \rbrace$ は潜在的なトピック $z_{d, n} \in \lbrace 1, ..., K \rbrace$ を持っており、その文書のトピック分布とそのトピックの単語分布から生成されます。
z_{d, n} \sim \text{Categorical}(\boldsymbol{\theta}_d), \\
x_{d, n} \sim \text{Categorical}(\boldsymbol{\phi}_{z_{d, n}}).
学習アルゴリズムは変分ベイズを用いる方法とギブスサンプリングを用いる方法の2つがよく使われますが、ここでは変分ベイズについて紹介します。基本的には対数周辺尤度を最大化することが目的になりますが、変分ベイズ法では以下の式変形をします。式変形の過程については省略しますがイェンセンの不等式を用いると導出できます。
\log p(\boldsymbol{X}|\alpha, \beta) = F[q(\boldsymbol{Z}, \boldsymbol{\theta}, \boldsymbol{\phi})] + KL[q(\boldsymbol{Z}, \boldsymbol{\theta}, \boldsymbol{\phi})||p(\boldsymbol{Z}, \boldsymbol{\theta}, \boldsymbol{\phi}|\boldsymbol{X}, \alpha, \beta)], \\
F[q(\boldsymbol{Z}, \boldsymbol{\theta}, \boldsymbol{\phi})] = \int \int \sum_{\boldsymbol{Z}} q(\boldsymbol{Z}, \boldsymbol{\theta}, \boldsymbol{\phi}) \log \frac{p(\boldsymbol{X}, \boldsymbol{Z}, \boldsymbol{\theta}, \boldsymbol{\phi}|\alpha, \beta)}{q(\boldsymbol{Z}, \boldsymbol{\theta}, \boldsymbol{\phi})} d\boldsymbol{\theta}d\boldsymbol{\phi}.
このように式変形すると、新しく導入した $q(\boldsymbol{Z}, \boldsymbol{\theta}, \boldsymbol{\phi})$ が事後分布 $p(\boldsymbol{Z}, \boldsymbol{\theta}, \boldsymbol{\phi}|\boldsymbol{X}, \alpha, \beta)$ を近似する関数となり学習しやすいように自由に設計でき、平均場近似により各因子が独立、すなわち $q(\boldsymbol{Z}, \boldsymbol{\theta}, \boldsymbol{\phi}) = q(\boldsymbol{Z}) q(\boldsymbol{\theta}) q(\boldsymbol{\phi})$ だと仮定することで扱いやすくなります。さらに、その近似関数を事後分布に近づけるために$KL[q(\boldsymbol{Z}, \boldsymbol{\theta}, \boldsymbol{\phi})||p(\boldsymbol{Z}, \boldsymbol{\theta}, \boldsymbol{\phi}|\boldsymbol{X}, \alpha, \beta)]$ を最小化する問題から、変分下限と呼ばれる $F[q(\boldsymbol{Z}, \boldsymbol{\theta}, \boldsymbol{\phi})]$ を最大化する問題にできます。KLダイバージェンスを目的関数にすると事後分布 $p(\boldsymbol{Z}, \boldsymbol{\theta}, \boldsymbol{\phi}|\boldsymbol{X}, \alpha, \beta)$ が含まれているが、変分下限では結合分布 $p(\boldsymbol{X}, \boldsymbol{Z}, \boldsymbol{\theta}, \boldsymbol{\phi}|\alpha, \beta)$ に置き換わっているのでベイズの定理により条件付き確率に展開でき、計算が容易になります。
実験
ランサーズにはユーザーが自分のスキルを出品できるパッケージというサービスがあります。今回はこのパッケージを使ってトピックモデルを試してみました。勉強がてら自前で実装し、$K=10$ に設定しました。
結果
以下はトピック1の単語分布から確率が上位の単語とその確率です。
記事 0.098
執筆 0.028
文字 0.018
ライティング 0.017
経験 0.015
作成 0.015
ライター 0.014
おり 0.012
ジャンル 0.011
年 0.011
トピック7
広告 0.023
運用 0.019
SEO 0.013
サービス 0.011
サイト 0.011
企業 0.01
集客 0.009
アカウント 0.008
マーケティング 0.008
さ 0.008
トピック8
動画 0.041
撮影 0.031
編集 0.018
写真 0.018
制作 0.016
3 0.012
いたし 0.011
ください 0.01
https 0.009
映像 0.008
トピック10
作成 0.022
開発 0.017
資料 0.017
システム 0.013
する 0.011
アプリ 0.01
事業 0.008
業務 0.008
管理 0.008
対応 0.006
トピック1はライティング関連、7は広告・マーケティング関連、8は動画関連、10はプログラミング関連と人目で見ても教師なしで納得感のあるトピックが学習できているように見えます。 またプログラミング・システム開発カテゴリにあるパッケージを適当に抽出し、そのトピック分布を計算してみると以下のようなトピックの確率を出力しました。
トピック10 0.723
トピック9 0.098
トピック2 0.032
...
終わりに
この記事ではトピックモデルを使ってランサーズのデータに適用してみました。トピックモデルは様々な拡張モデルがあり、階層構造を学習できるものや、新しいトピックの出現などを分析できる時系列を考慮できるモデルなどあります。こちらの記事ではユーザーからの問い合わせを分類や時間的な変化などを分析し、サービス改善につなげているようです。パッケージでは150以上の中カテゴリがあり、ユーザーが出品するパッケージにより今後新しいカテゴリが作られることもあると思います。そのときにトピック数を動的に推定することもできるモデルなどを用いて増やすべきカテゴリなどを自動的に検知できたりするかもしれません。