0. Advent Calendar 2021 19日目です

初めまして、tomolatoonです。書き始めた時はC++ Advent Calender 2021が結構空いていたので、自分も記事を投稿してみようと思って書きました。~~書いている本人が理解できてないなんて言えない~~

18日目 | NoSQLドキュメント指向組み込みデータベースCouchbase Lite 3.0.0 ベータにおけるC/C++サポート
20日目 | OpenCL C++ on NVIDIA GPU

2023/03/27 §1. の読みやすさ・内容を改善しました。

0.1. 導入と注意

この記事は、メタ関数や関数を意図的に呼び出し分けるなどの、テンプレートを使ったコンパイル時のセカイ、特にメタ関数について説明しているものです。単純な関数テンプレートやクラステンプレートを定義したことがあることを前提にして進みます。

記事のコードは全てC++20を想定して書かれています。C++17以下で使用する際は気を付けてください。

1. メタ関数

メタ関数は「テンプレートのインスタンス化を利用して、コンパイル時に処理を行うクラステンプレート」である、と「C++テンプレートテクニック第二版」は定義しています。

実際にはより広く「主にコンパイル時に型操作をしたり、型の特性を返したりするもの」であると考えます。そうすると、メタ関数は以下のような特徴があります。

必ずテンプレートで実装される。特に、クラステンプレートとして実装されることが多い。
コンパイル時にテンプレートが実体化されることで評価される。実行時ではない。
引数はテンプレート引数、返り値はタイプエイリアスや静的メンバ。よって、引数と返り値は複数持てる。
扱うのは型やコンパイル時定数。

まずは、便宜上返すものが型かコンパイル時定数かで大きく二種類に分けて紹介します。

1.1. 型を返すメタ関数

型を返すメタ関数は、型の操作を行います。例えばconstを付けたり外したり、関数を呼び出した返り値の型を取得したり出来ます。

型を返すメタ関数では、タイプエイリアスtypeをメンバに定義し、それを返り値として扱うことが慣習になっています。

型を返すメタ関数とその使い方の例

// メタ関数
template <class T>
struct meta_func_for_type
{
	using type = T;
};

// 使い方
meta_func_for_type<int>::type // int

1.1.1. エイリアステンプレートに包む

しかし、このように実装されたメタ関数は::typeを付けて結果の型を取得しなければならず、面倒です。特に、C++17 以前は常にtypenameキーワードを前置する必要があり、尚更面倒です。

そのため、型を返すメタ関数はその名前に_tを付けたエイリアステンプレートに包まれることが慣習となっています。（なので、C言語時代からある類似機能typedefは使えません。typedef は C++11 ではオワコンです。）

エイリアステンプレートに包まれたメタ関数とその使い方

// エイリアステンプレート
template <class T>
using meta_func_for_type_t = meta_func_for_type<T>::type;

// 使い方
meta_func_for_type_t<int> // int

1.2. コンパイル時定数を返すメタ関数

コンパイル時定数を返すメタ関数は、特に型特性を取得するものが有用です。例えば、constが付いているか、あるメンバを持っているか、などがあります。なお、標準ライブラリには、コンパイラマジックによって実装されるメタ関数も存在していたりします。

参考: type_traits - cpprefjp C++日本語リファレンス

型を返すメタ関数では、コンパイル時定数を返すメタ関数は静的メンバvalueを返り値として扱うことが慣習になっています。

コンパイル時定数を返すメタ関数とその使い方の例

// メタ関数
template <bool B>
struct meta_func_for_value
{
	static constexpr bool value = B;
};

// 使い方
meta_func_for_value<true>::value // true

1.2.1. std::integral_constant

整数のコンパイル時定数を返すメタ関数は、std::integral_constantを継承することで、より簡単に定義することが出来ます。

std::integral_constant の使い方

template <size_t I>
struct integral : std::integral_constant<size_t, I>
{};

// 使い方
integral<0>::value // 0

1.2.2. std::bool_constant、std::true_typeとstd::false_type

bool値のコンパイル時定数を返すメタ関数は、std::bool_constantを継承して実装することで、更に、true/falseを返すメタ関数はstd::true_type/false_typeを継承することでより簡単に定義出来ます。

std::bool_constant 及び std::true_type/false_type の使い方

template <bool B>
struct true_false : std::bool_constant<B>
{};

template <bool B>
struct always_true : std::true_type
{};

template <bool B>
struct always_false : std::false_type
{};

// 使い方
true_false<true>::value   // true
always_true<false>::value // true
always_false<true>::value // false

1.2.3. 変数テンプレートで包む

どの方法を使ったにせよ、型を返すメタ関数と同様に::valueを付けるのが面倒なことには変わりありません。

コンパイル時定数を返す関数の場合は、変数テンプレートで包むことで回避することが出来ます。メタ関数はコンパイル時定数しか扱えないのでconstepxrを、更にinlineも付けておいたほうがよいでしょう。

// 変数テンプレート
template <bool B>
inline constexpr bool meta_func_for_value_v = meta_func_for_value<B>::value;

// 使い方
meta_func_for_value_v<true> // true

1.3. 例1 - add_const

ここからは、標準ライブラリで実装されているメタ関数のうち、簡単なものをいくつか実装することでメタ関数を紹介していきます。

まずは、std::add_constと同じことをするadd_constを実装してみましょう。このメタ関数はテンプレート引数で受け取った型にconstを付けて返すメタ関数です。実装としては単純で、テンプレート仮引数にconstを付けたものをエイリアス宣言すればいいわけです。

add_const

template <class T>
struct add_const
{
	using type = const T;
};

// 使い方
add_const<int>::type;       // const int
add_const<const int>::type; // const int

add_const - cpprefjp C++日本語リファレンス

1.4. 例2 - is_void

さてconstを付けたので次は外す...のではなく、一旦別のことをしましょう。constを外すのは §1.6. で扱います。ここでは、テンプレート実引数がvoidであるかを判定するstd::is_void相当のis_voidを実装しましょう。

1.4.1. テンプレートの特殊化

関数がオーバーロードによって複数定義を用意できるように、テンプレートの場合は特定の型や値の並びに対する別定義を用意する「テンプレートの特殊化」をすることが出来ます。

ここで、大本のテンプレートのことを「プライマリーテンプレート」、別定義のことを「特殊化」と呼びます。

特殊化ではテンプレート宣言におけるテンプレート仮引数の個数がプライマリーテンプレートと一致する必要がありません。代わりに、識別子の後に<>を付与し、そこにプライマリーテンプレートに対応する型や値の並びを指定します。

1.4.2. テンプレートの完全特殊化

テンプレートの特殊化の中でも、テンプレート仮引数が無く、「全て」具体的な型や値で指定されている場合は「テンプレートの完全特殊化」と呼びます。

というわけで、テンプレート宣言はtemplate <>となり、識別子の後の<>には全て具体的な型と値を指定したものがテンプレートの完全特殊化です。

テンプレートの完全特殊化を用いて、is_voidは次のように実装することが出来ます。

is_void

template <class T>
struct is_void : public std::true_type
{};

template <>
struct is_void<void> : public std::false_type
{};

// 使い方
is_int<int>::value  // true
is_int<void>::value // false

is_void - cpprefjp C++日本語リファレンス

1.5. 例3 - is_same

ここでは、2つのテンプレート引数で受け取った型がcv修飾を含めて同じ型かを判定するstd::is_same相当のis_sameを実装します。

1.5.1. テンプレートの部分特殊化その1

完全特殊化とは対照的に、テンプレート仮引数が残っている特殊化は「テンプレートの部分特殊化」と呼びます。

というわけで、テンプレート宣言でテンプレート仮引数が1つでも宣言されて、識別子の後の<>にはそれを用いて指定をしたものがテンプレートの部分特殊化です。もちろん、具体的な方や値を併用しても問題ありません。

テンプレートの部分特殊化を用いて、is_sameは次のように実装することが出来ます。

is_same

template <class T, class U>
struct is_same : std::false_type
{};

template <class T>
struct is_same<T, T> : std::true_type
{};

// 使い方
is_same<int, int>::value  // true
is_same<int, int&>::value // false
is_same<std::add_const_t<int&>, int&>::value // true

is_same - cpprefjp C++日本語リファレンス

1.6. 例4 - remove_const

それでは §1.3. とは逆に、テンプレート引数で受け取った型からconstを消すメタ関数std::remove_constと同じことをするremove_constを実装するにはどうすればいいでしょう。

1.6.1. テンプレートの部分特殊化その2

テンプレートの部分特殊化は、もう1つ面白い仕様があります。型テンプレート仮引数と共に、型修飾子を用いると、該当する型修飾子が付いているかどうかで部分特殊化することが出来ます。例えば次のように。

修飾子のパターンマッチを利用した部分特殊化の例

template <class T>
struct X {};

template <class T>
struct X<T&> {};

lvalue reference が付いているテンプレート実引数に対する特殊化を提供しています。つまり、lvalue reference が付いている型に対しては下の実装が選択されるわけです。具体的にはintやdoubleは上、int&やdouble&は下が選択されます。

更に注目したい機能は、部分特殊化のテンプレートでは特殊化したい型修飾子をベタ書きすることで、べた書きしている部分をテンプレート仮引数と分離出来る、ということです。

今回は、&（lvalue reference）がベタ書きされているので、例えばX<int&>の場合にはT = intとなり、lvalue reference は分離されることになります。

1.6.2. 実装してみよう

前述の通り、テンプレートの部分特殊化を用いれば型修飾子をテンプレート仮引数から分離することが出来ます。そのため、remove_constはテンプレートの部分特殊化を用いて次のように実装することが出来ます。

remove_const

template <class T>
struct remove_const
{
	using type = T;
};

template <class T>
struct remove_const<const T>
{
	using type = T;
};

// 使い方
remove_const<int>::type;       // int
remove_const<const int>::type; // int

remove_const - cpprefjp C++日本語リファレンス

1.7. 例4 - add_result

ここまでテンプレート引数で受け取った型に修飾子を合成したり、部分特殊化によって分解したりなどをしてきました。ここでは、所謂「型の値」という概念を説明します。

例としては、標準ライブラリにあるものではないです（このあと紹介する機能そのものを使ってしまえばいいので当然ではあります）が、ある型の値とある型の値を足した結果の型を返すメタ関数add_resultを作ります。

1.7.1. 値カテゴリ

本題に入る前に、少し難しめの概念について紹介しておきます。C++ における「式（最終的に評価されて1つの値になるもの）」の文脈で登場する「値カテゴリ」というものです。

元々の出自に遡れば、値カテゴリとは 「左辺値（代入の左辺に現れるもの）」と「右辺値（代入の右辺に現れるもの）」 でした。

古代的値カテゴリ

int i;

i; // これは左辺値
0; // これは右辺値

// 左辺値は代入の左辺に、右辺値は代入の右辺に現れる
i = 0;

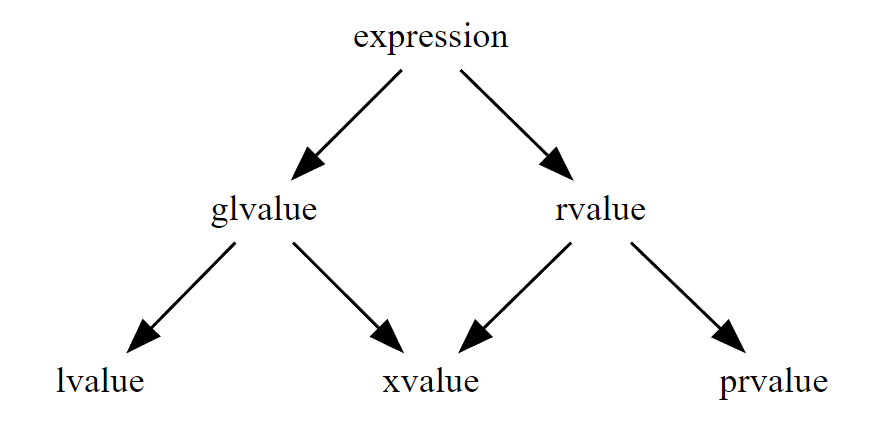
しかし、段々とこの定義での「右辺値」と「左辺値」は段々と正確では無くなってきました。C++ においては、C++11 で導入された rvalue reference に伴って値カテゴリの再定義を行うことになり、値カテゴリは次のような5種類に細分化されました。なお、説明は（定義からは程遠い）大まかなものなので、詳しくは他のページを参照してください。

lvalue: 名前が付いているもの、文字列リテラル、lvalue reference など。一般的に言う「左辺値」。
xvalue: rvalue reference のこと。lvalue を rvalue reference にキャストした値が主。
pvalue: リテラル値やコンストラクタ呼び出しなどで得られる値、参照ではない関数の返り値など。
glvalue: lvalue + xvalue のこと。究極的にメモリ上にあるオブジェクトを指しているもの全般。影が薄い。
rvalue: xvalue + pvalue のこと。名前がついていないもの全般。一般に言う「右辺値」。

ここで登場する lvalue を束縛できるのが lvalue reference、rvalue に束縛できるのが rvalue reference だ、ということになります。ただし、const lvalue reference は全ての値カテゴリを束縛することが出来ます。

なお、型で値カテゴリを表現する場合は、lvalue を lvalue reference で、rvalue を rvalue reference か non-reference で表現することが多いです。場合によっては、より細分化して xvalue を rvalue reference で、pvalue を non-reference で表現することもあります。（例: lvalueをint&、xvalueをint&&、pvalueをint）

正しく & 詳しくは: 値カテゴリ - cppreference.com

1.7.2. decltype

decltypeは指定された式の型を取得してくれる言語機能で、「型の値」を用いる場所としても活躍します。次のように使います。

decltype による型取得例

int a; double b;

decltype(a)              // int
decltype((a))            // int&, あれ？

decltype(std::move(a))   // int&&
decltype((std::move(a))) // int&&

decltype(int{})          // int
decltype((int{}))        // int

decltype(a + b)          // double
decltype((a + b))        // double

取得されるのは型そのものなので、こうやって使うことも出来ます。

取得した型をそのまま使う

int a; double b;

decltype(a + b) c = a + b; // double  c = a + b;
decltype((c))   d = c;     // double& d = c;
decltype(c)&    e = c;     // double& e = c;

ここで大切なのは、decltypeに書いてある式は評価（≒計算）されない（未評価文脈である）ことです。仮に関数呼び出しがdecltype内にあったとしても、実際に呼び出されることがないので、関数定義は必要ではありません。

1.7.3. decltype の推論規則

さて、具体的な推論規則は、正確ではないですが大体次のような感じになります。括弧がない場合、識別子が宣言時の型に推論されることに注意してください。§1.7.2. のコードで「あれ？」となっていたのはこれが理由です。

式`e`（その式の型から参照を外した部分の型を`T`）の分類	括弧なし	括弧あり
構造化束縛の識別子	構造化束縛先の型	識別子の「括弧なし」推論に準ずる
識別子・メンバアクセス	その識別子の宣言における型	下3つのどれかで分類
上記以外の lvalue	`T&`	`T&`
xvalue	`T&&`	`T&&`
pvalue	`T`	`T`

※: 構造化束縛の識別子の場合は不可解な挙動をするんですが、どなたかわかる人は教えてください… 再現のwandboxはこちらです

正しく & 詳しくは: decltype 指定子 - cppreference.com

1.7.4. std::declval

こちらが本題の「型の値」の話です。std::declvalは「型の値」を作るものとしてその名が付いた、次のような宣言だけ（定義がない）テンプレート関数です。（std::add_rvalue_referenceは、rvalue referenceを追加するメタ関数です。）

namespace std
{
	template <class T>
	add_rvalue_reference<T>::type declval();
}

次のように使います。

decltype(std::declval<int&>())                         // int&
decltype(std::declval<int>())                          // int&&
decltype(std::declval<int>() + std::declval<double>()) // double

decltype(int{})などと書いていたのをstd::declvalに変更している形であることがわかるかと思います。「型の値」というのは、未評価文脈で意味論上、ある型のある値カテゴリを表すものなのです。

ところで、§1.7.2. のコードのことを思い出せば、0も1もint{}もstd::declval<int>()も全て「型の値」として見做せることは勘付くかと思います。ではなぜstd::declvalにするか、と言うと、次のような理由が考えられます。

リテラル表記が存在しない型が多数存在しているから。
コンストラクタの引数が多かったり、複雑であったりすると、std::declvalよりも書くのが大変になるから。
コンストラクタがprivateであったり、deleteされている場合、そもそもコンストラクタを用いて書けないから。
std::declvalは 「型の値」を作るために使用すると C++ プログラマーの間で共通認識が存在するから。

1.7.5. 参照の圧縮

§1.7.4. のコードで示したように、ある型Tの lvalue はstd::declval<T&>と書けば得られます。これは、次のような「参照の圧縮」がstd::rvalue_referenceで起こっていることで達成されています。

まず前提として 「ポインタへのポインタ」は存在しますが、「参照への参照」は存在しません。というのも、そもそも参照はオブジェクトではないし、あるオブジェクトoへの参照aを使って参照bを初期化しようとしても、bはaへの参照ではなくoへの参照になるように設計されているからです。

ところで、通常では構文としても「参照への参照」は作成できないようになっていますが、テンプレート仮引数に対しては「参照への参照」かのように見える状況が起こり得ます。そのような場合に「参照の圧縮」が発生します。

template <class T>
struct add_rvalue_reference
{
	using type = T&&; // Tに参照が含まれている時は参照の圧縮が起こる
};

具体的には、次のような4パターンが考えられますが、次のように圧縮されます。どちらも&&であれば&&に、それ以外は全て&になる、という感じです。

`T = U??`（元の型）	`T??`（追加する参照）	`U??`（圧縮結果）
`&`	`&`	`&`
`&`	`&&`	`&`
`&&`	`&`	`&`
`&&`	`&&`	`&&`

1.7.6. 実装しよう

少し長くなってしまいましたが、「型の値」という考え方を用いて、「ある2つの型TとUの値に対して二項演算子operator+を適用した結果の型」を返すadd_resultメタ関数を実装してみましょう。実装は次のようになります。

template <class T, class U>
struct add_result
{
	using type = decltype(std::declval<T>() + std::declval<U>());
};

// 使い方
add_result<int, int>::type;    // int
add_result<double, int>::type; // double

1.8. 例5 - rank

ここでは、テンプレート引数に組み込み配列を渡すと、その組み込み配列が何次元なのかを返すメタ関数rankを実装してみましょう。ただし、組み込み配列では無い型に対しては0を返すことにします。（intなら0を、int[1]なら1を、int[1][1]なら2を、という感じで返します。）

1.8.1. 組み込み配列かどうかの判定

そもそも、組み込み配列かどうかを判定するにはどうすればいいでしょうか。この場合は、テンプレート引数を追加して、2つのテンプレート引数で組み込み配列を表現して特殊化することになります。例えば、組み込み配列の要素数を取得するsizeメタ関数は次のように書くことが出来ます。

template <class T>
struct size : std::integral_constant<size_t, 0>
{};

template <class T, size_t N>
struct size<T[N]> : std::integral_constant<size_t, N>
{};

ちなみに組み込み配列の中でも「要素数が決定していない」ものであるT[]が存在しますが、その場合の要素数は0として処理することにして、今回は特殊化しないで済ませています。

1.8.2. N次元への拡張

さてここで更にもう1つ課題があることに気づくかと思います。というのも、先程の §1.8.1. でやった通りに実装すると、次元数を取得出来るのは精々1次元で、2次元以上に対応できません。どうすればいいでしょうか。

1.8.3. 再帰的に適用する

結論としては、 「組み込み配列かどうかの判定」を再帰的に（何度も）適用していけばよいです。例えば、int[1][2]があった時は、1次元目を部分特殊化で取っ払いint[2]にして、更にもう一度部分特殊化を使えばintまで還元が可能です。この再帰的に次元を取っ払う作業中に、テンプレート引数で何回次元を取っ払ったかを受け渡ししていけば、最終的にそれが次元数を表す値になるはずです。

ちなみに、あんまり再帰が深すぎるとコンパイラが火を噴きますが、次元はそこまで大きくなることがないので問題ありません。

1.8.4. 実装してみよう

今回は、2種類のクラスを用いて実装しています。ユーザーからはrankを使ってもらい、そこからrank_implを呼び出して実際の処理を行います。（ちなみに、implは「実装」を意味する英単語implementationのこと。）

ただし1つ注意したいのが、メタ関数sizeの時と違い、要素数が不明な配列も次元を持っていると見做します。なので、rank_implは2つの部分特殊化を持つことになります。実装例は次のようになります。

template <class T, size_t I>
struct rank_impl
{
	constexpr static size_t value = I;
};

template <class T, size_t I>
struct rank_impl<T[], I>
{
	constexpr static size_t value = rank_impl<T, I + 1>::value;
};

template <class T, size_t N, size_t I>
struct rank_impl<T[N], I>
{
	constexpr static size_t value = rank_impl<T, I + 1>::value;
};

template <class T>
struct rank : std::integral_constant<size_t, rank_impl<T, 0>::value>
{
};

呼び出される順番を箇条書きに起こすと次のようになります。

rank<T>からrank_impl<T, 0>を呼ぶ
1. Tが組み込み配列ではない
  1. rank_impl<T, I>のプライマリーテンプレートが選ばれて終了
2. Tが組み込み配列
  1. Tは要素数が決まっていない組み込み配列
    1. rank_impl<T[], I>が選ばれる
    2. 更にrank_impl<T, I+1>を呼びだす
    3. Tが組み込み配列かどうかの判定に戻る
  2. Tは要素数が決まっている配列
    1. rank_impl<T[N], I>が選ばれる
    2. 更にrank_impl<T, I+1>を呼び出す
    3. Tが組み込み配列かどうかの判定に戻る

参考: rank - cpprefjp C++日本語リファレンス

1.9. メタ関数を定義するのに便利なメタ関数

最後に、メタ関数を定義するのに便利なメタ関数の、std::conditonalを紹介します。std::conditonalは<bool, 型, 型>の3つのテンプレート引数をとり、第1引数がtrueなら第2引数を、第1引数がfalseなら第3引数を返すメタ関数です。つまり、型のif文というわけです。

次のように実装することが出来ます。わざわざ2種類特殊化を定義する必要はなく、プライマリーテンプレートと特殊化でtrueかfalseのそれぞれに対応すればいいわけです。

template <bool F, class T, class U>
struct conditional
{
	using type = T;
};

template <class T, class U>
struct conditional<false, T, U>
{
	using type = U;
};

参考: conditional - cpprefjp C++日本語リファレンス

2. 型特性とSFINAE

さて次に行きますが、型特性というのは「constが付いているか」というような簡単なものから、「クラスかどうか」のようなもの、突き詰めていくとコンパイラーマジックによって実装されるものまであります。ここでは、SFINAEを紹介しつつ型特性に関するメタ関数をいくつか実装していきます。

2.1. SFINAEとは

もう説明尽くされている気がしますが、「SFINAEって何？」から見ていきます。SFINAEは「Substitution Failure Is Not An Error」の略。日本語だと「（テンプレート引数の）置き換え失敗は（コンパイル）エラーではない」ということになります。

ですから、SFINAEは「型特性に応じてオーバーロードやテンプレートの実体化を選択する」や、「型制約を付ける」などの場合で使用されます。~~C++20なんだからConceptを使えって？それは後にさせてください…~~

Wikipediaの例が分かりやすいので、Wikipediaから引用したコードを見てください。コード中のtypedef int foo;は、エイリアス宣言のusing foo = int;と等価です。なお、前述の通りtypedef は C++11 ではオワコンなです。

引用元：SFINAE - Wikipedia

struct Test {
    typedef int foo;
};

template <typename T> 
void f(typename T::foo) {} // 定義#1

template <typename T> 
void f(T) {}               // 定義#2

int main() {
    f<Test>(10); // #1の呼び出し
    f<int>(10);  // #2の呼び出し（int::fooがないので#1では失敗するはずだが、SFINAEのおかげでコンパイルエラーにならず、#2が評価される）
}

コメントに書いてあることで全てなのですが、ある型Tがタイプエイリアスfooを持っていれば上のテンプレートが、fooを持っていなければ下のテンプレートが選択されるわけです。

では、SFINAEの仕様について、お手頃なSFINAE - cppreference.comに当たってみましょう。以下引用中の強調は、全て私が後から付けています。

2.1.1. SFINAEのすべてはそこに置かれている

このルールは関数テンプレートのオーバーロード解決中に適用されます。 テンプレート引数に対する明示的に指定されたまたは推定された**型の置換が失敗したとき、**コンパイルエラーが発生する代わりに、その特殊化がオーバーロード集合から取り除かれます。

太字にした部分を繋げて読んでみましょう。「関数テンプレートのオーバーロード解決中にテンプレート引数に対する型の置換が失敗したとき、その特殊化がオーバーロード集合から取り除かれます。」つまりそういうことです。

2.1.1.1. オーバーロード

というのも少しひどいので、言葉を足しておきます。そもそもC++の関数は「シグネチャ」と呼ばれる、関数を識別する要素（関数の名前、引数の型の並びなど）が異なることで別の関数として宣言が可能です。

参考: signatureの定義 - yohhoyの日記

その中でも、関数の名前が同じでありながら、関数の名前以外のシグネチャが異なるために複数の関数が定義できることを「（関数）オーバーロード」と呼びます。

// 関数f はオーバーロードされている
void f() {}
void f(int) {}

2.1.1.2. オーバーロード解決

詳しくは後で触れますが、オーバーロードされた関数たちは、使用されるタイミングでそのうちの1つに決定されることになります。この実際に使用する関数を決定するのをオーバーロード解決と言い、このオーバーロード解決に参加する関数の集合を「候補関数」と呼びます。

この候補関数を決定する際、関数テンプレートは関数テンプレートそのものとして候補関数に参加するのではなく、テンプレート引数を決定してから通常の関数と同様の扱いになって候補関数に参加することになります。

2.1.1.3. つまり

関数テンプレートのオーバーロード解決中に

オーバーロードされた関数たちを集めて「候補関数」という集合にまとめ、そこから実際に使用する関数を決定するプロセスにおいて、

テンプレート引数に対する型の置換が失敗したとき、

テンプレート関数はそのプロセスのうち「候補関数」に参加する際にテンプレート引数を確定させており、その際にC++としてエラーになるようなコードが出来たとしてもコンパイルエラーにせず、

その特殊化がオーバーロード集合から取り除かれます

その失敗したテンプレート関数のオーバーロードを「候補関数」から取り除く（に参加させない）ことだけに留めておく

ということになります。

2.1.2. 任意の式によるSFINAE

任意の式によるSFINAE - cpprefjp C++日本語リファレンスには、

C++03において、SFINAEによって「型Tに関する任意の式が有効かどうかを判定できるか」は仕様として曖昧だった。C++11ではこの曖昧さが取り除かれ、任意の式が有効かどうかでSFINAEが処理されることとなった。

また、

置き換えは、関数型、テンプレートパラメータ宣言および(もしあれば)テンプレート要件の中で使用される、全ての型と式に起こる。式は、非定数式を許可するsizeof、decltypeおよび他のコンテキストの内部の配列の範囲、あるいは非型テンプレート引数として現われるもののような定数式だけでなく、一般的な式(つまり非定数式)も含んでいる。

とあります。テンプレート仮引数や関数のシグネチャにおいて、式もSFINAEの対象になるわけですね。つまり、decltype中に式を書いてSFINAEをすることが出来るということを示唆しています。

2.2. 実際に使ってm…ちょっと待った！

SFINAEがする事は痛い程分かりましたが、SFINAEを実際に使用するにはテンプレート関数を含めた関数オーバーロードの解決規則が分からないとどうしようもないわけです。関数オーバーロードの解決について確認していきます。

ここからは以下のcppreference.comのページを参照していきます

2.2.1. 名前探索

オーバーロード解決のページを見ると、まず関数が使用された時に、その使用された文脈に応じて呼び出されうる関数が名前探索され、候補関数の集合として用意されます。この際、ADL（Argument Dependent Lookup、実引数依存の名前探索）を起こす時もあったりと忙しいのですが、今回は重要ではないのでバッサリと割愛します。

2.2.2. 型の置換が行われるタイミング

さて、名前探索が行われた次に関数テンプレートは「テンプレートの実引数推定」を行うそうです。ところで、SFINAEの方のページを参照すると、以下のように書いてあります。

関数のテンプレート仮引数の置換 (テンプレート実引数への置き換え) は2回行われます。
・ 明示的に指定されたテンプレート実引数はテンプレートの実引数推定の前に置換されます。
・ 推定された実引数とデフォルトから取得された実引数はテンプレートの実引数推定の後で置換されます。

どうやら、関数テンプレートのテンプレート仮引数が実引数に置換されるのは「実引数推定」の前と後の2回行われるということだそうです。ということは、名前探索が終わったタイミングで「明示的に指定されたテンプレート実引数」をテンプレート引数に置換し、そこでSFINAEが発生しうるようです。

2.2.3. 実引数推定

関数テンプレートのページに移ります。ページの例を見ると「実引数推定」の名前通り、関数テンプレートの実引数からテンプレート引数を推定する作業です。このとき、

仮引数が参照でない場合、組み込み配列と関数はポインタに変換して扱われる
- 例えば、実引数のT[1]はT*として扱われる
- もちろん、仮引数がT&なら実引数の配列は配列として参照に束縛される
仮引数のトップレベルのcv修飾子は削除したものとして扱ってオーバーロード解決をする
- 例えば、仮引数がconst TならTとして扱われる
- もちろん、関数の中ではconst Tのconstは付いているものとして扱われる
- もちろん、const T&など参照・ポインタのcv修飾子は維持される

という規則が働くことは通常の関数と同様ですね。この実引数推定の直後に2回目の型の置換が行われ、ここでもSFINAEが発生しうるという認識で良さそうでしょう。
なお、ここまででテンプレート引数を置換し終わった関数テンプレートは、以後は通常の関数と同様に扱われます。

2.2.4. その後（実行可能関数・最良実行可能関数）

続けてオーバーロード解決のページを読んでいきます。ここまでの手順で候補関数が収集された後に、実際に呼び出しされている文脈で呼び出しが可能かどうか判断され実行可能関数の集合が形成されます。更に実行可能関数の集合の中で、ある1つの関数が他の関数に比べて「優先度が高い」場合にオーバーロード解決が成功するという手順となっているようです。

2.2.5. 最良実行可能関数の選ばれ方

まず実行可能関数の集合のすべての関数において、実引数リストと仮引数リストの各引数についてどれだけ「暗黙の変換」が「良い」かを判定します。この時に、ある2つの関数の組に対して、その「暗黙の変換」の「良さ」を比較し、すべての引数についてどちらか片方が「良さ」で勝っている時、その勝っている関数を「より良い関数」と定義します。

そうして、実行可能関数の集合のすべての関数の組に対してこの「より良い関数」を決定することを繰り返し、ある実行可能関数がその他すべての実行可能関数よりも「より良い関数」となった時、その実行可能関数が最良実行可能関数として選ばれます。

とにかく重要なのは、最良実行可能関数が一意に1つに定まった時だけ、オーバーロード解決が成功することです。SFINAEの文脈で最良実行可能関数がどれかを判断し、一意にプログラムを書くためにひとまず覚えておきたい重要なルールは次のものです。

通常の関数は、同じ仮引数リストを持つ関数テンプレートよりも優先される
プライマリー関数テンプレート同士はより実引数に近い形の仮引数を持つものが選ばれる
- プライマリーテンプレートが選ばれた後、初めてそのテンプレートの特殊化が考慮される
  - 特殊化同士は、より特殊化しているものが選ばれる
可変長引数を持つ関数は最も優先されない

2.3. decltypeを使って式によるSFINAE

それでは、SFINAEを使って型特性を取得するメタ関数を書いてみましょう。まずは、ある型がswapという関数を呼び出せるかどうかを判定するstd::is_swappableメタ関数です。（といっても、標準ライブラリとはかなり仕様が異なるのですが、目をつぶってください...）

swap関数というのは、2つの変数の値をそれぞれ交換する関数のことを想定しています。なので、例えば次のような実装が出来ます。

template <class T>
struct is_swappable_impl
{
private:
	template <class T>
	static auto impl(T& t) -> decltype(std::swap(t, t), std::true_type{});

	static auto impl(...) -> std::false_type;

public:
	using type = decltype(impl(std::declval<T&>()));
};

template <class T>
struct is_swappable : ::is_swappable_impl<T>::type
{};

// 使い方
// ムーブコンストラクタとムーブ代入演算子削除して使えなくしたクラス
// std::swap はムーブ構築とムーブ代入演算子で実装されるハズなのでCは使えなくなる
struct C
{
	C(C&&) = delete;
	C& operator=(C&&) = delete;
};
is_swappable<int>::value; // true
is_swappable<C>::value;   // false

ポイントは、std::true_typeの方のimpl静的メンバ関数の返り値にdecltypeを用いて具体的な式を書いている点と、std::false_typeの方のimpl静的メンバ関数を可変長引数にしている点です。

それによって、std::swap(t, t)という式が実行可能なら上（下も使用できるが、可変長引数は優先されない）、実行不可能であれば下（SFINAEが発動して上は候補関数から除外される）を選択することが出来ています。

ちなみに、std::swap(t, t), std::true_type{}の3つ目の,はコンマ演算子で、左辺の結果を破棄して右辺の結果を式の結果とする演算子です。

なお、std::declvalを使わずにstd::true_type{}と書いたのは、std::declvalを使うとdecltypeの推論でstd::true_type&あるいはstd::true_type&&となるからです。

2.4. std::enable_ifを使って型特性を利用する

最後はメタ関数を作るのではなく、メタ関数を利用してみましょう。

2.4.1. std::enable_if

std::enable_ifは、<bool, 型>という2つのテンプレート引数を取ります。第1引数がtrueの時は第2引数の型を返し、falseであれば第2引数を返さないどころか、タイプエイリアスtypeすら宣言しません。つまり、std::enable_ifは、次のような実装になっています。

template <bool F, class T = void>
struct enable_if
{
	using type = T;
};

template <class T>
struct enable_if<false, T>
{};

enable_if - cpprefjp C++日本語リファレンス

2.4.2. 使ってみる

ではどうやって使うかというと、std::enable_ifの第1引数にテンプレートパラメータに対して課したい性質をメタ関数で表現した論理式で書き、第2引数に関数の返り値の型（本来必要な型）を書きます。

こうすることで、テンプレートパラメータ置換時に論理式がfalseになる（＝テンプレート実引数が課している条件を満たさない）とtypeが定義されなくなります。結果、テンプレートパラメータ置換に失敗し、SFINAE を意図的に発生させられます。

例えば、整数か小数かで実装を分けるのは次のように出来ます。（std::enable_if_tの方を使います）

template <class T>
auto sample(T t) -> std::enable_if_t<std::is_integral_v<T>, T>
{
	std::cout << "integral" << std::endl;
	return t;
}

template <class T>
auto sample(T t) -> std::enable_if_t<std::is_floating_point_v<T>, T>
{
	std::cout << "floating_point" << std::endl;
	return t;
}

int main()
{
	sample(0);
	sample(0.);
}

もちろん、出力はこうなります。

integral
floating_point

2.5. 整数でも小数でもない型向けも欲しくなったら

先程の例で、もし整数でも小数でもない型の分岐を付けたくなった場合はどうすればいいでしょうか。先ほどの例だと3つほど解決策があります。

2.5.1. 脳筋する

1つ目の解決策としては、脳筋で「整数でも小数でもない」という条件を準備して、それをstd::enable_ifに渡すことです。この解決策は単純明快ですが、条件が増えたら詰むという点と記述が冗長になる欠点があります。~~Boost PPとかで生成すれば大丈夫かもしれませんが。~~
この場合に追加する関数テンプレートは次のように実装できます。

template <class T>
auto sample(T t) -> std::enable_if_t<!(std::is_integral_v<T> || std::is_floating_point_v<T>)>
{
	std::cout << "other" << std::endl;
	return t;
}

int main()
{
	sample(std::vector<int>());
}

出力はこうなります。

other

2.5.2. 可変長引数でフォールバックとして対応

2つ目の解決策としては、フォールバックの形にはなりますが可変長引数を使用することです。可変長引数の関数は関数オーバーロードの解決での優先順位が最も低ことは既に書いた通りです。
なので、整数や小数の方の関数が実行可能関数に残ればそちらを、残らなければ可変長引数の方が選択されるわけです。ただし可変長引数は型情報を捨てるので、1つ目の解決策のように取った引数を使用するのはほぼ不可能です。
次のように実装出来ます。

void sample(...)
{
	std::cout << "other" << std::endl;
}

2.5.3. 継承で優先順位を付ける

3つ目の解決策としては、継承を用いて意図的に関数オーバーロード時の優先順位を付けておく方法です。例えばある型TとUがありUがTを継承している場合、Uのオブジェクトが実引数の時、基底クラスであるTよりも優先的にUを仮引数に持つ関数にオーバーロード解決がされます。このことをコードで表わすと次のようになります。

struct T
{};

struct U : T
{};

void f(T) // #1
{}

void f(U) // #2
{}

int main()
{
	f(T{}); // #1が呼ばれる
	f(U{}); // #2が呼ばれる（#1も呼べるが、基底クラスよりも派生クラスが優先）
}

2.5.3.1. ヘルパーを用意しておく

この仕様を利用するために、次のテンプレートクラスrankを定義しておきます。

template <size_t I>
struct rank : rank<I - 1>
{};

template <>
struct rank<0>
{};

テンプレートクラスrankは、テンプレート引数Iでsize_tの値を取ります。そして、I-1をテンプレート引数にしたrankを継承します。rank<0>は特殊化して継承するのを止めます。そうすることで、rank<N>は、rank<N-1>からrank<0>までのN-1個のrankを継承することになります。

2.5.3.2. 関数テンプレートの方の実装を変えよう

なので、例えば次のように実装を変更すると上手く優先順位を付けて呼び出すことが出来ます。

template <class T>
auto sample(T t, rank<1>) -> std::enable_if_t<std::is_integral_v<T>, T>
{
	std::cout << "integral" << std::endl;
	return t;
}

template <class T>
auto sample(T t, rank<1>) -> std::enable_if_t<std::is_floating_point_v<T>, T>
{
	std::cout << "floating_point" << std::endl;
	return t;
}

template <class T>
auto sample(T t, rank<0>)
{
	std::cout << "other" << std::endl;
	return t;
}

整数と小数の実装はrank<1>を受け取るようにして、整数でも小数でもない型への実装はrank<0>を受け取るようにしておきます。そうすると、整数でも小数でもない型への実装だけ優先順位が低い状態にすることが出来ます。sampleを呼び出すには次のようにします。

int main()
{
	sample(0, rank<1>{});
	sample(0., rank<1>{});
	sample(std::vector<int>{}, rank<1>{});
}

今回、sampleはrank<1>までしか使用していないので、rank<1>以上のインスタンスを追加で渡すようにすればよいわけです。実行結果は次のようになります。

integral
floating_point
other

2.5.3.3. ラップしておくと安心

sampleはrankを自分で渡す必要があり、事故が起きやすいのでラップしておくと安心です。

template <class T>
auto sample_wrapper(T&& t)
{
	return sample(std::forward<T>(t), rank<1>{});
}

2.6. constexpr if使った方が良くない？…良くない？

実は、この長々と続いている例のSIFNAEはC++17で追加された機能のconstexpr if文を使用すればもっと簡単に書くことが出来ます。例えば、constexpr if文でsampleを実装すると以下のようになります。

template <class T>
auto sample(T t)
{
	if constexpr (std::is_integral_v<T>)
	{
		std::cout << "integral" << std::endl;
		return t;
	}
	else if constexpr (std::is_floating_point_v<T>)
	{
		std::cout << "floating_point" << std::endl;
		return t;
	}
	else
	{
		std::cout << "other" << std::endl;
		return t;
	}
}

constexpr if文は、通常のif文のifと条件を書く()の間にconstexprを付けたものになり、条件にはコンパイル時定数を指定する必要があります。条件がtrueなら真文、falseなら偽文の部分が実体化され、反対の部分は廃棄文として実体化が抑制されます。
つまり、条件によってコードの実体化させる部分を選択することが出来ます。例えば条件に型特性を返すメタ関数を書くと、型特性によってコードの実体化させる部分を選択することが出来ます。

2.6.1. Two-phase name lookupとconstexpr if文

constexpr if文を使うときには少し注意することがあります。先程「コードの実体化させる部分を選択」と書きましたが、この「実体化」がミソで、例えば次のようなコードはコンパイルエラーになってしまいます。¹

template <class T>
auto f(T t)
{
	if constexpr (std::is_unsigned_v<T>)
	{
		return t;
	}
	else
	{
		static_assert(false);
	}
}

これには「Two-phase name lookup」という言語機能が関係しています。Two-phase name lookupは二段階の名前探索などと日本語訳されますが、テンプレートな関数やクラスについて「その関数やクラスの定義が見つかった際にはテンプレート引数に依存しない文の、実際に定義が使用され実体化される時にテンプレート引数に依存する文の妥当性を検査する」という仕様のことです。

つまり、今回の例だとstatic_assert(false)はテンプレート引数に依存していないので、constexpr if文の条件式がどうであれ1段階目である「テンプレート関数fが見つかった際の妥当性の検査」で引っかかってしまう訳です。

P2593R1 及び CWG 2518 が C++11 への Defect Report として採用されたため、static_assertに限っては、条件式の内容に関わらず実体化が延期されることとなり、上記コードはコンパイルエラーを起こさなくなりました。

2.6.2. Two-phase name lookupの1段階目から逃げる

では、どうすれば1段階目の妥当性の検査を回避することが出来るかというと、テンプレート引数に依存するような体裁にすればいいわけです。いくつか方法はありますが、ダミーの変数テンプレートを使うかラムダ式を使うかが有名な解決策です。
次の例はコンパイルエラーせず、意図通りの動作をします。

template <typename T>
constexpr bool false_v = false;

template <class T>
auto f(T t)
{
	if constexpr (std::is_unsigned_v<T>)
	{
		return t;
	}
	else
	{
		static_assert(false_v<T>);
		static_assert([]() { return false; });
	}
}

変数テンプレートfalse_vはどんなテンプレート引数だろうとfalseを返す変数テンプレートで、ラムダ式は単純にfalseを返しているだけです。前者がテンプレート引数に形式上依存しているのはわかると思います。

後者は、そもそもラムダ式がクラスで実装される関数オブジェクトの糖衣構文ですから、テンプレート関数内で定義されるクラスは依存名（≒テンプレート引数に依存する）になるというルールが適用されます。なので1段階目から逃げることが出来たんですね。

3. コンセプト

C++20では、ついに全C++ユーザー待望[要検証]のコンセプトが導入されました。コンセプトはテンプレート引数に対して、満たさなければならない要件（beginメンバ関数を呼び出せるか、typeタイプエイリアスを持っているか、など）を課すことが出来ます。
詳しくはコンセプト - cpprefjp C++日本語リファレンスや制約とコンセプト (C++20以上) - cppreference.comを見て頂くことにして、簡単に説明します。

3.1. コンセプトの作り方

何の役にも立たないコンセプトは次のように定義することが出来ます。

template <class T>
concept useless_concept = true;

この例から分かるように、コンセプトの定義はテンプレート宣言 concept 識別子 = 制約式 ;という形で行います。コンセプトは制約式の結果に応じたただのbool値定数式として扱われます。
このとき、trueと評価される時は制約が満たされている、falseなら満たされていないという意味になります。

3.2. 制約式

制約式は、その名前の通り「テンプレート引数に要求する制約を表現した式」のことで、やっぱり「bool値定数式」のことです。制約式は原子制約式と連言（&&）と選言（||）で表現されますが、結局実体としてはbool値定数式なわけです。

3.2.1. 原子制約式とコンセプトやメタ関数

原子制約式は連言や選言が含まれていないような制約式のことですが、結局bool値定数式なのでコンセプトやbool値を返すメタ関数などを原子制約式として使用することが出来ます。
ちなみに、論理積/和演算子（&&/||）が連/選言として特別な意味を与えられている一方、論理否定演算子（!）は特別な意味を持ちません。したがって、論理否定演算子が付いていても原子制約式になります。

3.3. requires式

requires式は実際に制約を表現するときに使用する式で、原子制約式に分類されます。つまりこの式もbool値定数式です。requires式の中では要件というものを並べ、具体的な制約を表現します。ひとまず文法としては次のようになります。

// 引数リストがあるバージョン
requires( /*引数リスト*/ )
{
	// 1つ以上の要件
}

// 引数リストがないバージョン
requires
{
	// 1つ以上の要件
}

引数リストは関数のものとほとんど同様ですが、requires式の引数リストで導入された名前は実際に評価されることはありません。つまり既に説明した「型の値」を、std::declvalを使わずともわかりやすく用意できるわけです。

3.3.1. 要件

requires式の中では、単純要件、型要件、複合要件、入れ子要件の4種類を用いて制約を表現することが出来ます。なお、それぞれの要件も最終的にはbool値定数式として扱われます。
結局requires式がtrueになるためには、requires式が持っている要件がすべてtrueである必要があるわけです。

3.3.2. 単純要件

単純要件は純粋に、ある式が有効であることを要求する要件です。ここでの「有効」とはコンパイルに失敗しないくらいの意味で、実際に式を評価することはありません。したがって、式の評価結果を利用して制約をすることは出来ません。文法と例は次のようになります。

// 文法的には
任意の式 ;

// 例
// 同じ型同士で加算が出来る型を表すコンセプト
template <class T>
concept addable = requires(T a, T b)
{
	a + b;
};

任意の式が有効であればtrueに、有効でなければfalseに評価されます。

3.3.3. 型要件

型要件は、ある型が有効であることを要求する要件です。単純要件と同様に、「有効」とは型要件で指定されている名前が型を表していて、コンパイルに失敗しないくらいの意味です。文法と例は次のようになります。

// 文法的には（大雑把）
typename 型名;

// 例
template <class T>
concpet has_value_type = requires
{
	typename T::value_type;
};

型名が有効な型であればtrueに、有効な型でなければfalseに評価されます。

3.3.4. 複合要件

複合要件は、式の有効性、例外送出の可能性、式の結果の値の型の制約の3種類について一度に制約を掛けられる要件です。先に文法を示します。（以下での[]は省略可能であることを表します。）

// 文法的には
{ 任意の式 } [noexcept] [-> 式の結果の値の型の制約] ;

複合要件は指定されている制約について、それぞれ次のように検査を行い、すべてtrueであればtrueと評価されます。なお、式の結果の値の型の制約にはコンセプトを指定する必要があります。

式の有効性に関して
- 単純要件と同様に検査する
- true : 式が有効（=コンパイル可能）である
- false : 式が有効（=コンパイル可能）でない
例外送出の可能性について（noexceptが指定されている場合のみ）
- 式が例外を送出する可能性がないことを検査する
- true : 式が例外を送出する可能性がない
- false : 式が例外を送出する可能性がある
式の結果の値の型の制約について（指定されている場合のみ）
- 式の結果の値の型がコンセプトを満たしているかを検査する
- ただし「式の結果の値の型」はコンセプトの第1テンプレート引数に挿入される
- true : コンセプトを満たしている
- false : コンセプトを満たしていない

例は次のようになります。

// 例
// 同じ型同士で加算が出来る型を表すコンセプト（単純要件の場合と同じ）
template <class T>
concept addable = requires(T a, T b)
{
	{a + b};
};

// 引数なしで呼び出せ、例外を送出しない関数または関数オブジェクトを表すコンセプト
template <class T>
concept noexcept_invokable = requires(T a)
{
	{a()} noexcept;
};

// メンバ関数beginがint用の出力イテレータを返す型のコンセプト
template <class T>
concept begin_ret_iterator = requires(T t)
{
	{t.begin()} -> std::output_iterator<int>;
};

なおstd::output_iterator<Iterator, Type>は、IteratorがTypeを出力するための出力イテレータであることを表すコンセプトです。

3.3.5. 入れ子要件

入れ子要件は、requires式の中で更にbool値定数式を用いて制約を掛けるために使用出来る要件です。主に、requires式の引数リストで導入した識別子を利用して制約を掛ける時に使用します。文法としては以下のようになります。

requires 制約式 ;

制約式はコンセプトの定義の時の文法と同じなので、コンセプトでもメタ関数でもbool値定数式であればなんでも書くことが出来ます。例によって制約式がtrueであればtrue、falseならfalseとして処理されます。なので次のようなことが出来ます。

template <class T>
concept always_satisfied = true;

template <class T>
concept always_satisfied_requires_requires = requires
{
	requires true;
};

template <class T>
concept always_satisfied_requires_requires_requires_requires = requires
{
	requires requires { requires true; };
};

3.4. コンセプトの使い方

コンセプトの指定の仕方は3種類あり、それぞれを組み合わせて使用することができます。

// テンプレート引数の宣言で指定
template <std::integral T>
void f0(T t);

// autoプレースホルダと共に指定
void f1(std::integral auto t);

// requires節で指定
template <class T>
	requires std::integral<T>
void f2(T t);

std::integralを例として使ってみます。std::integralは指定したテンプレート引数に対して、組み込みの整数型であることを要求します。なので、今回のf0,f1,f2はそれぞれ、組み込みの整数型ではない値を引数にするとコンセプトで弾かれ、他に当てはまるオーバーロードがないのでコンパイルエラーになります。

3.4.1. テンプレート引数の宣言で指定

テンプレート引数の宣言で、classかtypenameを書いている場所にコンセプトを書く方法です。この方法は、テンプレート引数を1つしか取らないような単純なコンセプトで用いられることが多いです。（また、そのテンプレート引数の基礎的な特性を指定するのに使用することが多いようです）

// テンプレート引数の宣言で指定
template <std::integral T>
void f0(T t);

指定したコンセプトの第1テンプレート引数は、コンセプトを指定したテンプレート引数によって埋められます。なので複数のテンプレート引数を取るコンセプトは、第2テンプレート引数以降を明示的に指定すれば、この方法でも使用することが出来ます。

template <std::convertible_to<int> T>
void f(T t);

std::convertible_to<From, To>というコンセプトは、FromからToへとキャスト出来ることを要求します。この例ではstd::convertible_to<T, int>という意味になるので、テンプレート引数Tがintへと変換できることを要求しているわけです。

3.4.2. `auto`プレースホルダと共に指定

C++20では、ジェネリックラムダの構文に合わせて通常の関数でもautoプレースホルダを使ったテンプレートな引数の宣言が出来るようになりました。

// 関数の引数リストでautoプレースホルダ
void f_auto(auto t);

// こう書いた時と同じ
template <class T>
void f_template(T t);

そして関数の引数リストと返り値と変数宣言における、autoプレースホルダに対してコンセプトを指定する時は、autoプレースホルダの前にコンセプトを書きます。実際の効果については、「テンプレート引数で指定」と同等の動作をします。

// autoプレースホルダと共に指定
void f1(std::integral auto t);

3.4.3. requires節で指定

requires節は、テンプレート宣言がある場合はその直後に、非テンプレート関数なら「関数へのあらゆる修飾」や「後置返り値表記」の後に書くことが出来ます。requires節はその立地上すべてのテンプレート引数を使用することが出来、複数のテンプレート引数に跨るようなコンセプトをわかりやすく記述することが出来ます。

// 文法的には
requires 制約式

// requires節で指定
template <class T>
	requires std::integral<T>
void f2(T t);

requires節であれば連言（&&）と選言（||）を使って複数の制約をかけることが出来ます。もちろん、制約が全体としてtrueになればコンセプトを満たしている、falseになるとコンセプトを満たしていないということになります。requires節にrequires式を書くこともできるので、次のようなこともできます。

template <class T>
	requires requires(T t) { t.begin(); }
void f(T t);

3.4.4. それぞれのコンセプトの指定の仕方を使ってみた結果

using namespace std::literals;

f0(0);     // ok,    f0<int>
f1(0l);    // ok,    f1<long>
f2(0ll);   // ok,    f2<long long>

int a;
// f0(0.);    error, f0<double>     は`std::integral`で弾かれる
// f1(""s);   error, f1<std::string>も`std::integral`で弾かれる
// f2(&a);    error, f2<int *>      もやっぱり`std::integral`で弾かれる

3.5. コンセプトと関数オーバーロード

コンセプトは包摂関係があるかどうか、包摂関係があれば半順序についての判定がされます。簡単に言えば、複数のコンセプトの間で優先順位が付けられる場合は優先順位が付けられるというわけです。C++17以前では苦労していた関数オーバーロードへの優先順位付けは、コンセプトで簡単に達成できるわけです。
どのように包摂関係や半順序が判定されるのかということは非常に難しいので、ここでは言及を避けます。代わりに例示をしたいと思います。

template <class T>
concept integral = std::integral<T>;

template <class T>
concept wider_31_integral = std::integral<T> && requires(T t)
{
	requires sizeof(t) * 8 > 31;
};

template <class T>
concept wider_63_integral = wider_31_integral<T> && requires(T t)
{
	requires sizeof(t) * 8 > 63;
};

// #1
template <integral T>
void f(T)
{
	std::cout << "#1 integral\n";
}

// #2
template <wider_31_integral T>
void f(T)
{
	std::cout << "#2 wider_31_integral\n";
}

// #3
template <wider_63_integral T>
void f(T)
{
	std::cout << "#3 wider_63_integral\n";
}

int main()
{
	f('0'); // f<char>
	f(0);   // f<int>
	f(0l);  // f<long>
	f(0ll); // f<long long>
}

実行結果（LLP64）

#1 integral
#2 wider_31_integral
#2 wider_31_integral
#3 wider_63_integral

3.6. コンセプトで実装し直す

コンセプトの話が長くなりましたが、戻ってsampleの実装をコンセプトに変えてみましょう。sampleは、

引数を1つとり、それを返す。ただし、
引数が整数
- integralと改行を出力
引数が浮動小数点数
- floating_pointと改行を出力
引数がそれ以外
- otherと改行を出力

ということをするものでした。なので、次のように実装することが出来ます。

template <std::integral T>
auto sample(T t)
{
	std::cout << "integral" << std::endl;
	return t;
}

template <std::floating_point T>
auto sample(T t)
{
	std::cout << "floating_point" << std::endl;
	return t;
}

template <class T>
auto sample(T t)
{
	std::cout << "other" << std::endl;
	return t;
}

int main()
{
	sample(0);
	sample(0.);
	sample(std::vector<int>{});
}

もちろん実行結果は以下のようになります。

integral
floating_point
other

3.7. 「等しさを維持する式」

コンセプトをとりあえず使うのであればここまでで十分なのですが、正しく使うにはもう少し知っておくべきことがありますので解説します。
まず、コンセプト定義で用いられる概念として、「等しさを保持する式」というものがあります。「等しさを保持する式」というのは、ある式の定義域おいて、等しい入力が与えられた時に等しい出力が得られ、さらに安定である式のことを言います。これに関しては例を用いて説明します。

int n; std::cin >> n;

// これについて考える
1 / n;

上のコードでの1 / nにおいて、定義域はn != 0でないような入力、入力は1とn、出力は1 / nの結果の値であり、安定でもあるため、この式は「等しさを保持する式」です。詳しく説明します。

3.7.1. 入力

入力とは、ざっくりと言えばその式が持つオペランドの集合のことを指します。ここでは、その入力を構成する1つ1つのオペランドを引数と呼称します。ただし、std::move/forward/declvalの3関数についてはその関数呼び出しで1つの引数とみなします。これに従って、次で示す式たちは引数1つの入力からなる式です。

int a;

// これらは引数1つの入力からなる式（による式文）
a;
std::move(a);
std::forward<decltype(a)>(a);
std::declval<int>();

3.7.2. 定義域

定義域とは、その式の入力のうち有効でないような入力を除いた、入力の集合のことを言います。つまり数学の定義域と同じように、その式が意味を持てるような入力の集合のことを言います。先ほどの1 / nという例では、n == 0の時はゼロ除算となり式は定義しません。そのため、1 / nの定義域はn != 0であるような入力の集合であるわけです。

3.7.3. 出力

出力とは、その式によって変更された引数とその式が残した結果の値の集合のことを言います。ここでの引数は、定義域の節で言及した引数のことを指します。「等しさを保持する式」は、ここで言及された出力以外への副作用を伴ってはいけません。

3.7.4. 安定

ある式が「安定」であるとは、その式に対して複数回、同じ（等価？²）オブジェクトを用いた入力を行ったときに、そのオブジェクトに明示的な変更を伴わなければ等しい出力が得られる式（同じ入力があれば同じ出力をする式）であることを言います。「等しさを保持する式」は「安定な式」でもある必要があるため、「等しさを保持する式」は外部状態や内部状態に依存してはいけません

3.7.5. 結局…

結局「等しさを保持する式」は、「引数と結果の値以外への副作用を持たず、外部状態や内部状態に依存しない式」のことです。言い換えれば、入力がわかれば出力がわかるような式のことを指すわけです。

3.8. C++標準のコンセプトと「モデル」

C++標準のコンセプトでは、コンセプトそれ自体が検査する構文上の要件だけでなく、コンセプトの構文上で暗黙的に要求されている意味論的な要件や、文書でのみ記載されている意味論的な要件を守る必要があり、後者2つの意味論的要件をも満たしている時、「その型はそのコンセプトのモデルである」といいます。具体的には次のような要件があります。

3.8.1. requires式と「等しさを保持する式」による要件

C++標準で用意されているコンセプトでのrequires式で使用される式は、原則として「等しさを保持する式」であることを暗黙の内に要求しています。ただし、「正しさを保持することを要求しない」と特記されている場合は除きます。

3.8.2. 文書で追加で指定される要件

C++標準で用意されているコンセプトの説明に、追加で要求される要件が書かれていることがあります。これに関しては、それぞれのコンセプトについて確認していく他ないので、concepts - cpprefjp C++日本語リファレンスなどを参照して確認しましょう。

4. あとがき

結構頑張って書いているつもりなのですが、まだ扱いたい機能もたくさんありますし、読みやすさも足りていないと思うので、この後もまだまだこの記事は更新していくつもりです。頑張ります(/・ω・)/
↓
結構頑張りました…（コンセプトの追加）。読みやすさについてはまた今後で…

2021/12/21 「整数でも小数でもない型向けも欲しくなったら」、「constexpr if使った方が良くない？…良くない？」追加
2021/12/22 「いやこの記事C++20なんだからコンセプト使おうよ」執筆開始
2022/01/14 「いやこの記事C++20なんだからコンセプト使おうよ」追加
2022/02/2 「等しさを保持する式」、「C++標準のコンセプトと『モデル』」追加
2022/11/7 §3.7.4.「安定」について疑問が生じてきたので濁しを入れました
2023/03/27 §1. の読みやすさ・内容を改善しました

5. 参照

MSVCはガバガバなのでコンパイル通ります。かくいう私もMSVCの住民なのでコンパイル通るのびっくりしました。GCCやclangでもビルドする必要がありそうですね。 ↩
あるオブジェクトaと、aと等価な値を持つオブジェクトb、ある外部状態に依存せず内部状態のない関数fからなるf(a)という式について考えます。
このとき、「その式に対して複数回、同じオブジェクトを用いた入力を行った時の出力が等しい」ならf(a) == f(a)、「その式に対して複数回、等価オブジェクトを用いた入力を行った時の出力が等しい」ならf(a) == f(b)という解釈になります。どちらが正しいのでしょうか。
ここで、aとbをイテレータだと考え、f(x)を++x（前置インクリメント）とすると、前者は++a == ++a、後者は++a == +++bとなります。明らかに、後者のみ等号が成立します。
しかし、イテレータコンセプトでは前置インクリメントも「等しさを保持する式である（つまり安定でもある）」ことを要求されることがあります。つまり「前置インクリメントも安定たりうる」はずです。となると、前者の解釈ではこれに矛盾するので、後者の解釈を採用するべきだと思われます。
ですが規格書に当たると、「安定（stable）」とは「two evaluations of such an expression with the same input objects are required to have equal outputs absent any explicit intervening modification of those input objects」と書かれています。「等価」ではなく、「同じ」オブジェクトだ、って言っているように見えます。
さてこれは一体どこから間違っているのでしょう...（C++有識者の方々、助けていただけると幸いです） ↩

メタ関数だらけのコンパイル時世界