LoginSignup
47
37

More than 5 years have passed since last update.

C++Advent Calendar 2017Day 10
@kazatsuyu(白山 風露)

制約とコンセプトとオーバーロードと半順序

Last updated at Posted at 2017-12-10

制約とコンセプトとオーバーロードと半順序

昨年に引き続き二回目の C++ Advent Calender に参加させていただきます。昨年はC++17のことを書いたわけですが、C++17は先日無事にISO標準規格として発行され、各所の解説等も少しずつ充実していっているようです。

それはさておき、ここは気が早いですが次期C++規格であるC++2aの話題として、Concepts TSからドラフト入りした内容を語っていこうと思います。
まあ、本当のことを言うともうちょっと前に出したかった記事なのですが、主にやる気がなくて結局塩漬けしてしまっていたのですが。

制約とコンセプトが来るよ！

C++2aでは、ようやく、ついに、制約とコンセプトが入るようです。

11で見送られ、14で見送られ、17でもついぞ入らず、ようやく2aのドラフトに入りました。もちろんまだ確定していませんが、うまく行って欲しいものです。

これでようやく、頑張ってSFINAEを書いたり読んだりしなくても済むようになります。さらばstd::enable_if_t

その前に制約とかコンセプトってなんだよ、って方は、 @yohhoy さんの記事とか見に行くといいと思います。

さて、そんな制約とコンセプトを利用したオーバーロード解決のルールが結構複雑なので、ちょっと解説してみよう、というのがこの記事の趣旨です。

「制約」と「コンセプト」の違い

以前からコンセプトコンセプトと言っていたので私も慣れていないのですが、制約(constraint)とコンセプト(concept)は別物なので、予め解説しておきます。

制約

制約は、テンプレートに対する要求を表す論理式です。式は最終的に bool 型になる定数式ならなんでも構いません。ただし、暗黙変換可能であっても bool 以外の型の式は制約としては不適です。

また、複数の制約を組み合わせて新しい制約を作ることもできます。

制約を構成する式自体のことは制約式と言います

コンセプト

コンセプトは、制約に名前を付けたものです。したがって、コンセプトは制約の一種ですが、制約とコンセプトはイコールではありません。

予め定義されたコンセプトを利用すれば、制約の再利用や宣言の簡略化が可能です。

コンセプトは

template<typename T>
concept C = /* 制約式 */;

などのように定義されます。

特に、このように単一のテンプレート引数を取るコンセプトであれば、テンプレート引数リストの中で typename の代わりに

template<C T>
void f(T);

といったように利用できます。

なお、上記の文法はConcepts TSの時点から変化しており、また、このように文法を変える提案も出ていたりするようなので、規格が発行されるころにはまた色々変わっている可能性もあります。

オーバーロード解決の優先順位

オーバーロード複数の関数が候補に上がった場合、コンパイラはそれぞれの関数のシグネチャによって、優先順位を決定します。

そして、優先順位が一番高かった物が呼び出されます。同率一位が複数あった場合、どの関数を呼び出すべきか分からないので、コンパイルエラーとなります。

これは以前から存在した挙動で、例えば、 

template<typename T>
void f(T);
template<typename T>
void f(T*);

int x;
f(&x);

こんなパターンで、 f(T) ではなく f(T*) が呼び出されるのは、こちらの方が優先順位が高いからです。

なお、制約に関わらない優先順位のルールはここでは具体的に解説しません。

制約の追加に伴って、この優先順位にも新たに追加されたルールがあります。

制約以外は同一優先順位の関数に関して、

  1. 制約を伴うものと伴わないものがあった場合、制約を伴うものが優先される
  2. 共に制約を伴う2つの関数に関しては、制約の順序関係が比較可能な時に限って、より制約の強いものが優先される

というルールです。

1.のルールは簡単で、

template<typename T>
void f(T);

template<C T>
void f(T);

という2つの関数があった場合、コンセプト C を満たす型であれば、後者の関数が優先されるというだけです。

なお、コンセプト C を満たさない型に関しては、後者の関数がオーバーロード候補に上がらないため、前者の関数が選ばれます。

一方、2.のルールに関しては、「制約の順序関係ってなんだろう？」となるでしょう。

制約の順序関係

以下のような式は、全て制約式となり得ます。(式中のTはすべて任意の型です)

true;
false;
std::is_integral_v<T>;
sizeof(T) < 4;
require(T t) { t.f(); };
std::is_integral_v<T> && sizeof(T) < 4;
std::is_integral_v<T> || sizeof(T) < 4;

さて、これらの制約式は、3種に分類されます。連言、選言、原子制約式です。

連言(conjunction)

&& 演算子で結合された２つの制約からなる制約は、連言(conjunction)と言います。

連言は、以下のような性質を持ちます。

異なる制約を表す式 A と B に関して、

  • A および B の連言は A ∧ B と表される
  • A 、 B の両方が条件を満たしたとき、 A ∧ B は条件を満たしたとみなすことができる
  • A ∧ B は A よりも B よりも強い制約である

選言(disjunction)

|| 演算子で結合された２つの制約からなる制約は、選言(disjunction)と言います。

連言は、以下のような性質を持ちます。

異なる制約を表す式 A と B に関して、

  • A および B の選言は A ∨ B と表される
  • A または B の少なくとも一方が条件を満たしたとき、 A ∨ B は条件を満たしたとみなすことができる
  • A ∨ B は A よりも B よりも弱い制約である

原子制約式

連言でも選言でもない制約を、原子制約式(atomic constraint)と言います。

原子制約式は、以下のような性質を持ちます。

  • 制約式は論理OR式や論理AND式ではない
  • 制約式の評価結果は bool 型のコンパイル時定数である
  • ２つの制約式 A と B が同じ式から構成されている場合、 A と B は同一の制約である
  • それ以外の場合は、異なる制約とみなす

上記の例を3つに分類すると、

std::is_integral_v<T> && sizeof(T) < 4;

これが連言

std::is_integral_v<T> || sizeof(T) < 4;

これが選言

true;
false;
std::is_integral_v<T>;
sizeof(T) < 4;
require(T t) { t.f(); };

これらが原子制約式となります。

原子制約式は、同一の値を表す式であっても同一の式とは限りません。

例えば、 true == !false は常に成り立ちますが、原子制約式としての true と !false は別の制約式です。別の原子制約式なので、順序関係は比較不可能です。

なぜそうなっているかと言うと、理論上、全ての制約式に関して、同一の値を表すことができるかどうかを判定するのは不可能だからです1。

集合と制約

具体的に制約の順序関係を考えるには、集合と同じようにベン図を描いてみると分かりやすいのではないかと思います。

制約に名前を付けたものがコンセプトなので、以下、制約 $X$ を表すコンセプトを $C_X$ として考えます。

任意のコンセプト $C_A, C_B$ に関して、以下のいずれかの関係が成り立ちます。

  1. $C_A$ と $C_B$ は同一である
  2. $C_A$ は $C_B$ より強い制約である
  3. $C_A$ は $C_B$ より弱い制約である
  4. $C_A$ と $C_B$ に順序関係は成り立たない

一般に、任意の制約に対し、「制約を満たす型と定数の組」の集合を考えることが可能です。

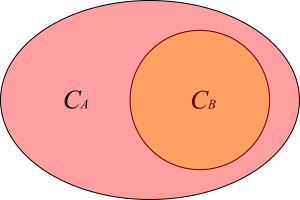
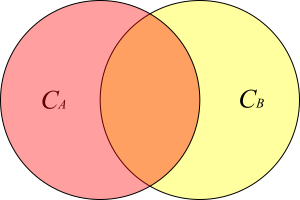
そこで、1から4の状態をそれぞれ対応する集合のベン図で表すと、

  1. CA=CB.png
  2. CA⊂CB.png
  3. CA⊃CB.png
  4. atomic.png

となります。

ベン図において、どちらか一方の集合がもう一方の集合を含んでいる場合、より図の面積の小さい集合が、より強い制約のコンセプトに対応しています。

一方で、4のように集合同士が重ならない領域を持つのであれば、制約の間に順序関係を定めることができなくなります。異なる原子制約式同士の関係は4になります。

なお、このような、部分的に比較可能な関係を半順序と言います。

制約の標準形

制約を定式的に比較するには、標準形(normal form)を作って比較する必要があります。

標準形が満たす条件は以下のようになります。

  • (E) の標準形は E の標準形である
  • E1 || E2 の標準形は E1 および E2 の標準形の選言である
  • E1 && E2 の標準形は E1 および E2 の標準形の連言である
  • C がコンセプト名のとき、 C<A1, A2, ..., An> の標準形は、C を定義する制約式のそれぞれのテンプレートパラメーターを A1, A2, ..., An に置き換えたものの標準形である
  • 上記以外の式 E の標準形は式 E で構成された原子制約式である

標準形には、以下の2種類があります。

  1. 連言標準形(conjunctive normal form)
  2. 選言標準形(disjunctive normal form)

連言標準形

以下の条件を満たす時、制約式 E は連言標準形と言います。

  • 制約式 E1, E2, ..., En を利用して、 E = E1 ∧ E2 ∧ ... ∧ En と表される
  • Ei (i = 1, 2, ..., n) は、原子制約式 Ai1, Ai2, ..., Aim を利用して、 Ei = Ai1 ∨ Ai2 ∨ ... ∨ Aim と表される。

選言標準形

以下の条件を満たす時、制約式 E は選言標準形と言います。

  • 制約式 E1, E2, ..., En を利用して、 E = E1 ∨ E2 ∨ ... ∨ En と表される
  • Ei (i = 1, 2, ..., n) は、原子制約式 Ai1, Ai2, ..., Aim を利用して、 Ei = Ai1 ∧ Ai2 ∧ ... ∧ Aim と表される。

正規化

全ての制約式は、分配法則や結合法則を利用して、上記どちらの形にも正規化可能です。

例えば、((A ∧ B) ∨ C) ∧ D という制約式は (A ∧ B ∧ D) ∨ (C ∧ D) という選言標準形に正規化されると同時に、 (A ∨ C) ∧ (B ∨ C) ∧ D という連言標準形に正規化されます。

標準形の半順序関係

異なる制約 A 、 B があったとき、 A ∧ B は A よりも強い制約で、 A ∨ B は A よりも弱い制約です。

このくらいの単純な形ならすぐにわかりますが、先程の例のような、
((A ∧ B) ∨ C) ∧ D

という制約式と、
A ∨ D
という制約式があった時に、どちらが強い制約か、あるいは、順序関係が成り立たないかを一見して判定することは難しいでしょう。
A ∧ B のような単純な形であればパターンを用意しておけば判定できますが、全ての制約同士の半順序関係を確かめるには、どんな形にも対応できるアルゴリズムを用意しておく必要があります。

そこで、以下のような方法を使います。

  • 制約式 $P$ と 制約式 $Q$ に関して、 $P$ を選言標準形、 $Q$ を連言標準形に正規化する
  • $P$ の選言標準形の各項 $P_i$ が、 $Q$ の連言標準形のそれぞれの項 $Q_j$ 以上の強さの制約である場合に限って、 $P$ は $Q$ 以上の強さの制約である
  • $P_i$ の中のある原子制約式 $P_{i_a}$ が、 $Q_j$ の中のある原子制約式 $Q_{j_b}$ 以上の強さの制約である場合に限って、 $P_i$ は $Q_j$ 以上の強さの制約である
  • 原子制約式 $A$ が原子制約式 $B$ と等価な制約式である時に限って、 $A$ は $B$ 以上の強さの制約である

以上の条件を一見してどういうことか分かる人はかなり数学に強い人だと思います。私はそこまで集合論に明るくなかったので、これを理解するのに丸一日かかりました。 という訳で、具体例を見てみましょう。

$P$ を ((A ∧ B) ∨ C) ∧ D 、 $Q$ を A ∨ D とします。
$P$ を選言標準形に正規化すると、 (A ∧ B ∧ D) ∨ (C ∧ D) になり、 $P_1 =$ A ∧ B ∧ D 、 $P_2 =$ C ∧ D となります。
$Q$ はこのままで既に連言標準形であり、 $Q_1 =$ A ∨ D です。
$P_1$ と $Q_1$ を比較すると、 $P_1$ の第一項 A と $Q_1$ の第一項 A が等価な原子制約式のため、 $P_1$ は $Q_1$ 以上の強さの制約であることが分かります。

また、 $P_2$ と $Q_1$ を比較すると、 $P_2$ の第二項 D と $Q_1$ の第二項 D が等価な原子制約式のため、 $P_2$ は $Q_1$ 以上の強さの制約であることが分かります。

以上から、 $P$ は $Q$ 以上の強さの制約であることが分かりました。

逆も調べるため、 $P$ を A ∨ D 、 $Q$ を ((A ∧ B) ∨ C) ∧ D とします。
$P$ はこのままで既に選言標準形であり、 $P_1 =$ A 、 $P_2 =$ D となります。
$Q$ を連言標準形に正規化すると、 (A ∨ C) ∧ (B ∨ C) ∧ D になり、 $Q_1 =$ A ∨ C　、 $Q_2 =$ B ∨ C 、 $Q_3 =$ D となります。

このとき、 $P_1$ と $Q_2$ を比較すると、 $P_1$ 中の各項と $Q_2$ 中の各項で順序関係がある組がありません。

以上から、 $P$ は $Q$ 以上の強さの制約ではないことが分かりました。

上記より、
((A ∧ B) ∨ C) ∧ D は A ∨ D 以上の強さの制約であり、
A ∨ D は ((A ∧ B) ∨ C) ∧ D 以上の強さの制約ではないことから、
((A ∧ B) ∨ C) ∧ D は A ∨ D より強い制約と判断することができます。

例

実際のところ、そこまでわけがわからなくなるような、複雑な制約を書くことはそうそうないと思います。

とりあえずコンセプトを使っておなじみのFizzBuzzでもやってみましょう。

#include <iostream>
#include <utility>

template<int n>
concept Fizz = n % 3 == 0;
template<int n>
concept Buzz = n % 5 == 0;
template<int n>
concept FizzBuzz = Fizz<n> && Buzz<n>;

template<Fizz n>
void output() {
    std::cout << "Fizz" << std::endl;
}

template<Buzz n>
void output() {
    std::cout << "Buzz" << std::endl;
}

template<FizzBuzz n>
void output() {
    std::cout << "FizzBuzz" << std::endl;
}

template<int n>
void output() {
    std::cout << n << std::endl;
}

template<int ...numbers>
void fizz_buzz(std::integer_sequence<int, numbers...>) {
    (output<numbers>(), ...);
}

int main() {
    fizz_buzz(std::make_integer_sequence<int, 100>());
}

gccに実装されているconceptはちょっとだけ文法が異なるのですが、実際に実行してみるとこんな風になります。

https://wandbox.org/permlink/2phlg4OHiOI61M99

終わりに

なんとか12/10中に間に合いました、かね……？

なぜいつもギリギリにならないと書けないのか。

以下、スペシャルサンクス（辞書順）

akinomyogaさん(@akinomyoga)
Kazutoshi SATODAさん(@k-satoda)
yohさん(@yohhoy)
yumetodoさん(@yumetodo)
いなむ先生(@_EnumHack)
いるやん‏さん(@Iruyan_Zak)

この文章を書くにあたって、色々指摘を頂きました。公開が遅くなって申し訳ありません。ありがとうございました。

  1. true と!false だけのような簡単な式なら判定できますが、テンプレート引数を受け取る場合、全ての引数に関して同一の値を返すかどうか調べることはできません。 ↩

47
37
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
47
37