この記事内でのサンプルコードは,最新版のG-coordinator ver3との互換性がありません.
今後,ver3に対応して修正いたします.編み形状を実現するための考え方は同じなため,その点を参考にする程度にとどめていただけますと幸いです.
G-coordinatorで編み造形
3Dプリンタで編み形状を利用したプロダクトとして,新工芸舎のtildeが有名です.こうした形状は,通常のモデリングソフトででメッシュを作成してスライス,という方法では作成することが困難です.そこで,今回は,この編み形状をG-coodinatorで再現する方法と,そのためのスクリプトの解説を行います.最終目標として,この写真に示すボウルを作ることを目指します.
最後にスクリプトを示しますので,G-coordinatorのエディタにスクリプトをコピペしてもG-codeはつくれますが,どこで何をしているのかが分かればみなさんが自分で造形する時の助けになるはずです.

円柱壁の造形
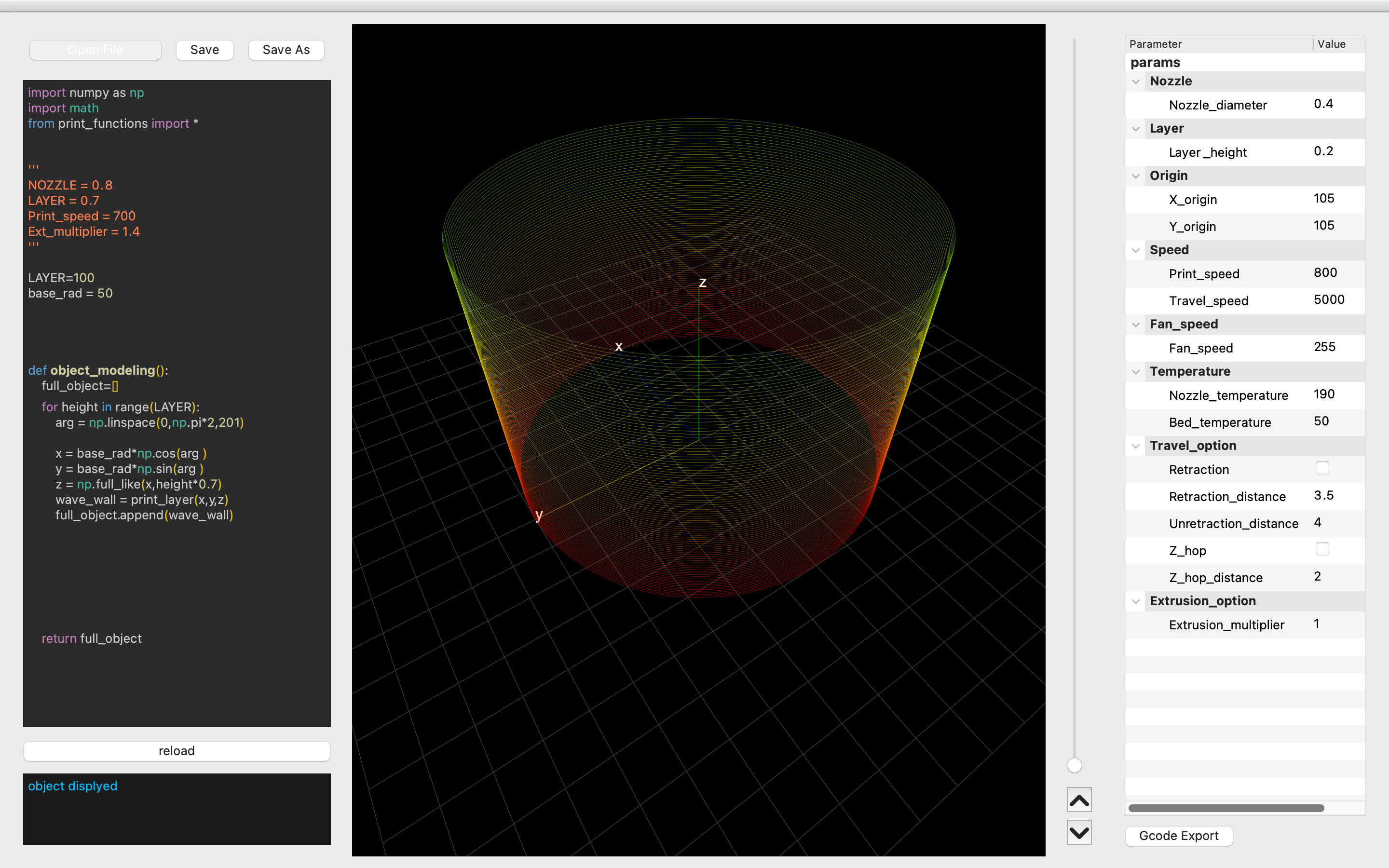
まずは円柱を造形するスクリプトです.
import numpy as np
import math
from print_functions import *
'''
NOZZLE = 0.8
LAYER = 0.7
Print_speed = 700
Ext_multiplier = 1.4
'''
LAYER=100
base_rad = 50
def object_modeling():
full_object=[]
for height in range(LAYER):
arg = np.linspace(0, np.pi*2,201)
x = base_rad*np.cos(arg )
y = base_rad*np.sin(arg )
z = np.full_like(x, height*0.7)
wave_wall = print_layer(x, y, z)
full_object.append(wave_wall)
return full_object
この辺りは#1とほとんど同じです.forの中身を見てみると,argが中心角,で,base_radにsin, cosをかけてx, yを計算しています.
argが要素数が201のndarryなので,x, y, z共に同じ要素数のndarrayが生成されます.
要素の数が201なのは,これが頂点の数だからです.

例えば,4角形だと,ノズルは1〜5番の頂点を順に移動していきます.移動する辺が4つあるので,これを構成する頂点は4+1個必要です.
すなわち,上のスクリプトでは,正200角形が描画されているわけです.
計算したx, y, zの頂点のリスト(正確にはndarray)をprint_layer()という関数に渡して,その返り値をfull_objectというリストに加えていきます.この点に関しては,他の記事で詳細を述べます.
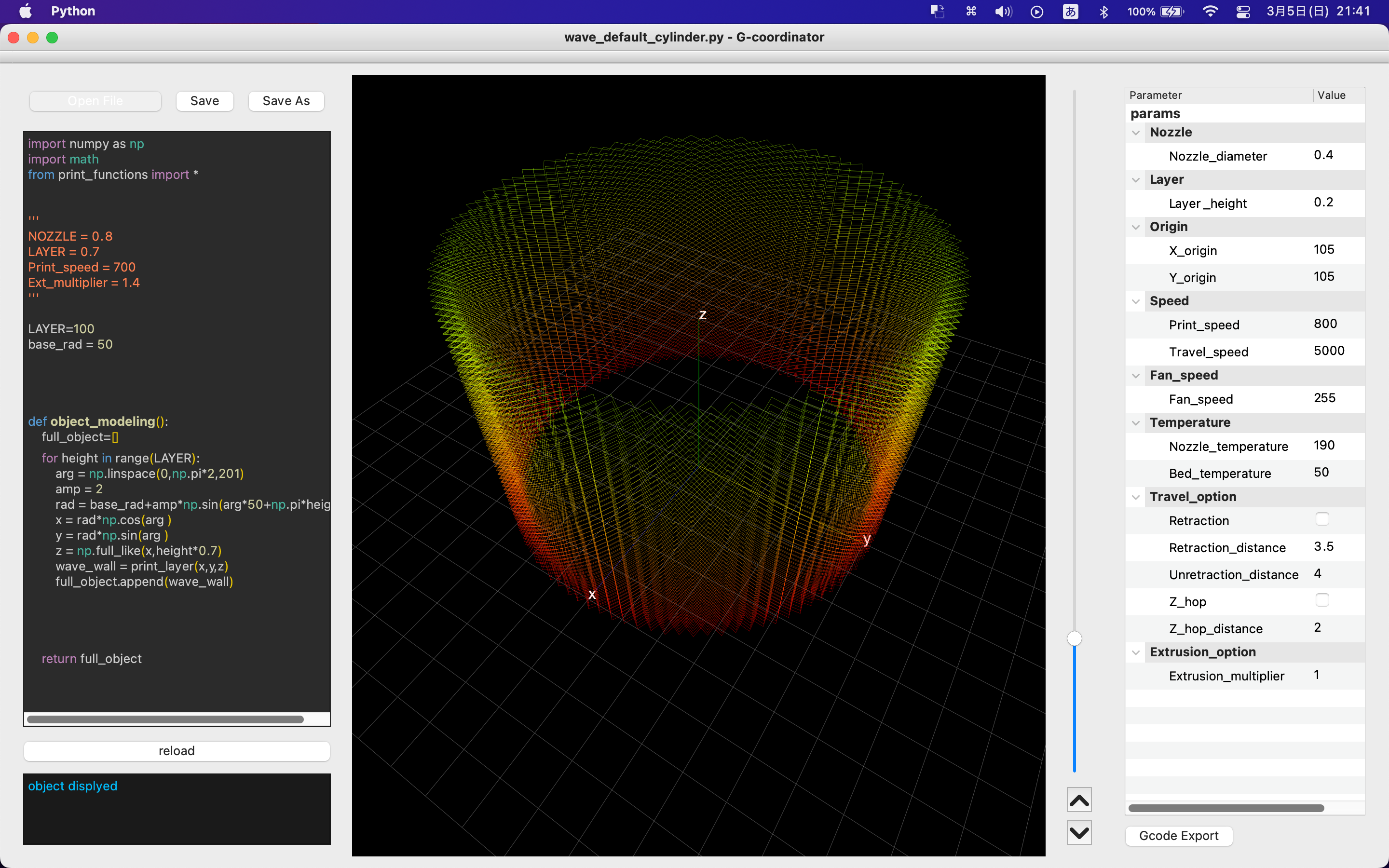
編み形状の実装
import numpy as np
import math
from print_functions import *
'''
NOZZLE = 0.8
LAYER = 0.7
Print_speed = 700
Ext_multiplier = 1.4
'''
LAYER=100
base_rad = 50
def object_modeling():
full_object=[]
for height in range(LAYER):
arg = np.linspace(0, np.pi*2,201)
amp = 2
rad = base_rad+amp*np.sin(arg*50+np.pi*height)
x = rad*np.cos(arg )
y = rad*np.sin(arg )
z = np.full_like(x, height*0.7)
wave_wall = print_layer(x, y, z)
full_object.append(wave_wall)
return full_object
先ほどのスクリプトとの違いは,radという新しい変数を導入しています.定数であるbase_rad にsinで振動を与えてやることで,ノズルがジグザグに移動します.
rad = base_rad + amp * np.sin(arg*50+np.pi*height)
ampは振幅です.
argは0から2πまでですので,sin(arg)で一回振動が起きます.argに50をかけたものをsin に渡すことで,ノズルが一周する間に振動が50回起きるわけです.
その後に,np.pi * heightを入れているのは,位相を調整するためです.各レイヤーごとに,heightは1ずつ大きくなっていきます.そのため,sin波の位相を各レイヤーごとにπずつずらすことにより,互い違いの編み模様になっていきます.
sin波の一回の振動を4つの直線で表すと考えると,直線の数は4×50 = 200それに1を加えて要素数を201にしておけば,綺麗に形状が生成されます.
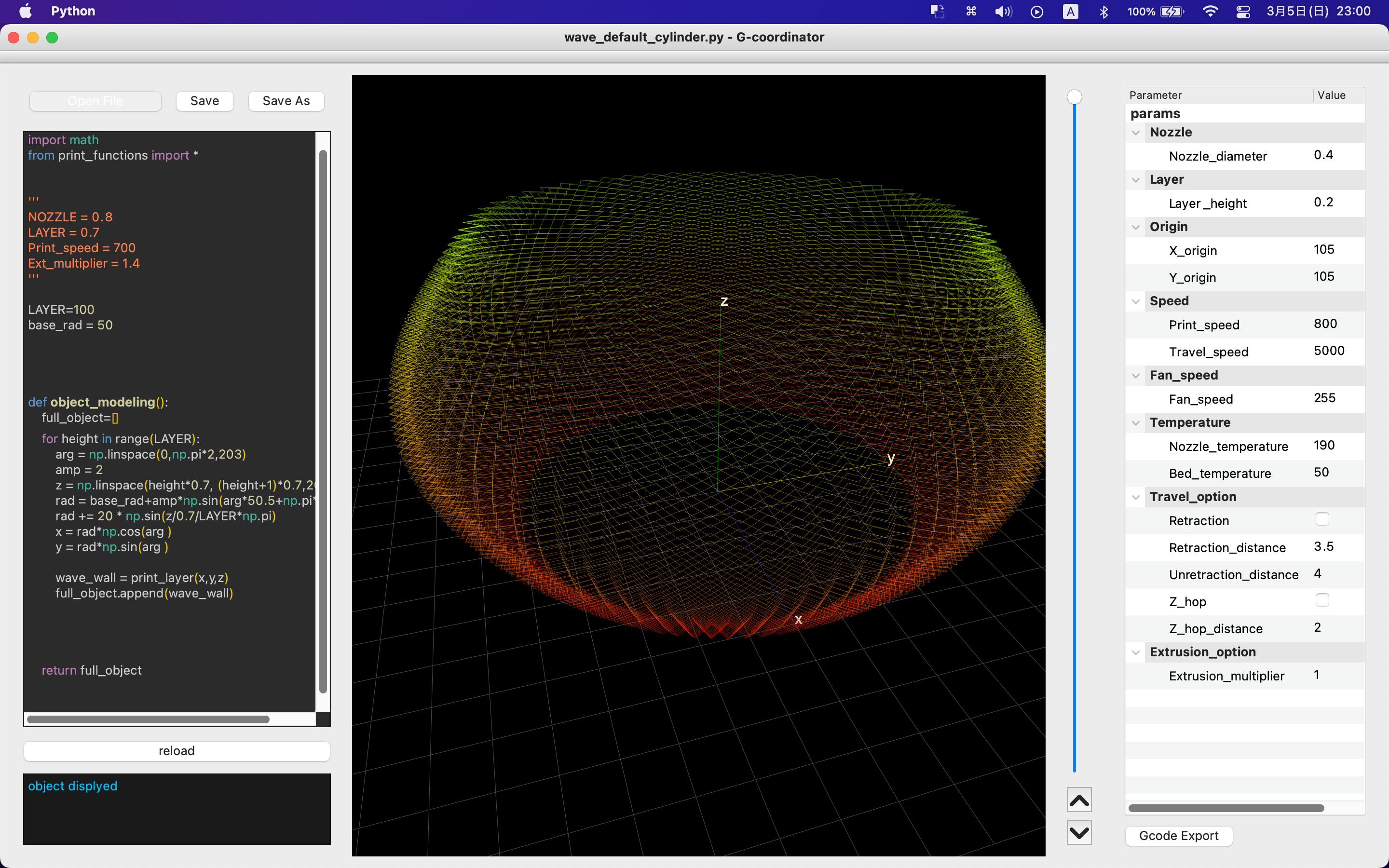
円柱側面を膨らませる
円柱のままでも,編み形状は綺麗ですが,側面の形状を工夫するとさらに面白いです.
上のスクリプトでradを計算した行の下に以下を追加してみてください.(上の画像参照)
rad += 20 * np.sin(height/LAYER*np.pi)
これは,各レイヤーごとに,sin関数で計算した半径のふくらまし量を足しています.
heightは0〜LAYER-1まで各レイヤーごとに増えていくので,height/LAYERで0〜1まで増えていきます.そこに,πをかけてsinに渡すことで,0層目からLAYER-1層目まででsin波の半周期となります.
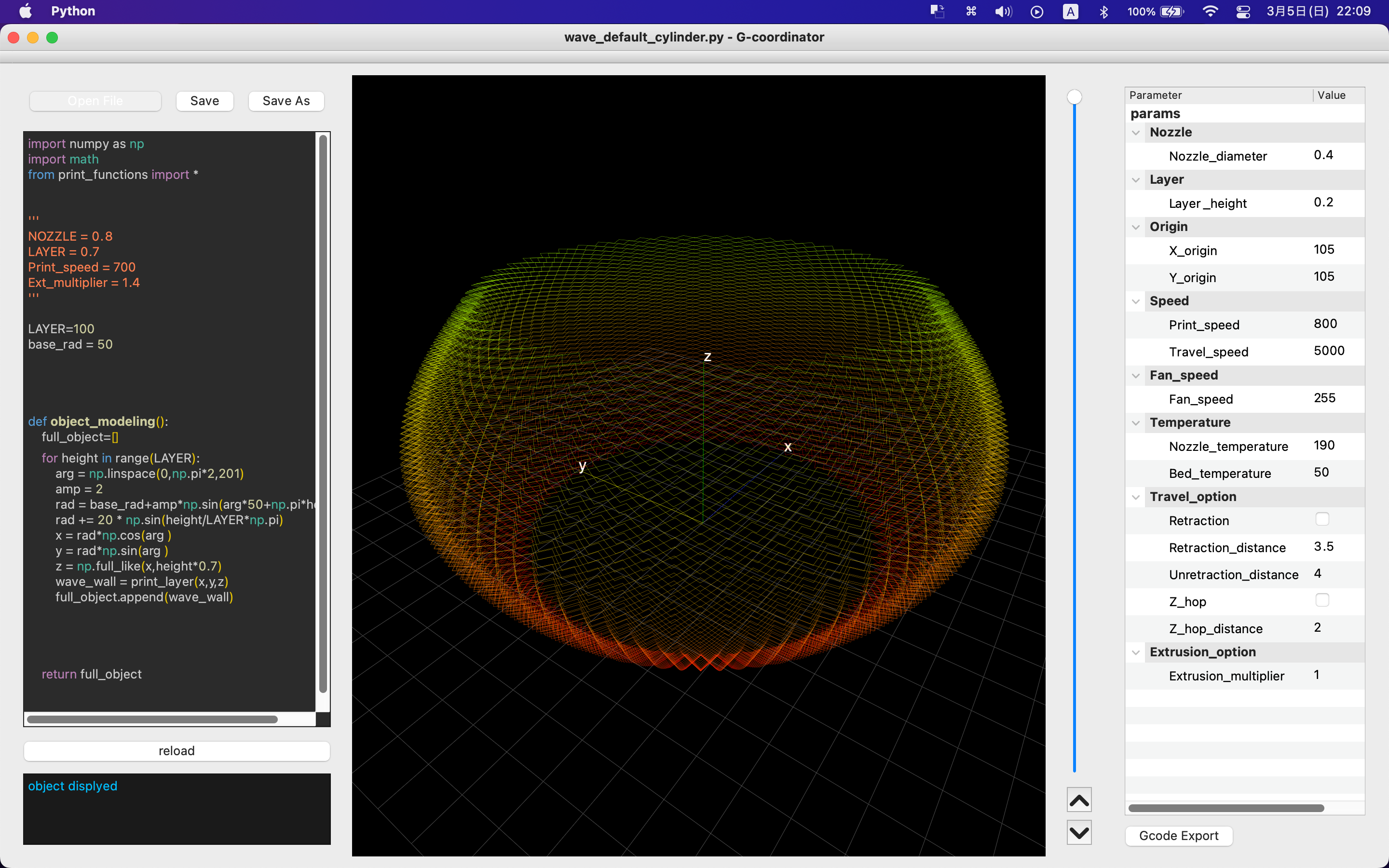
スパイラルモードの実装
以上でなんとか編みを再現することはできましたが,まだ少し問題があります.それは,Zシームです.3DPユーザの方なら悩まされることも多少あると思います.Zシームをなくすための一つの解決策として,スパイラルモードが挙げられます.curaにも実装されているので,使ったことのある人は多いかもしれません.
この章ではスパイラルモードの実装に関する説明をしますが,この辺りから少し込み入った内容になってきて,難易度が上がると思われます.
正直,気にならなかったら,あんまり真剣に読まなくても大丈夫です.
まず,各点のz座標の計算方法を修正します.
前回のスクリプトのzに関して
z = np.full_like(x, height*0.7) #これを消す
z = np.linspace(height*0.7, (height+1)*0.7, 201) #これに書き換え
上のスパイラルでない方は,各レイヤーの全てのz座標がheightにレイヤーの高さ0.7をかけたものとして計算していました.
下のスパイラルでは,linspace関数を用いてそのレイヤーの初めの高さheight*0.7から次のレイヤーの高さ(height+1)*0.7まで201段階で徐々に上がっていきます.
これでz座標は段階的に増えていきます.
円柱壁ならこれで終わりなのですが,今回のように,半径が振動しているものでは,もう少し処理が必要です.
この写真のように第n層目とn+1層目のラインが綺麗に接続されていないからです.
まず,次の層との位相を合わせるために,振動をもう半周期増やします.
rad = base_rad+amp*np.sin(arg*50.5+np.pi*height)
それに合わせて要素数は50.5×4+1 = 203に調整.
次に,側面を増やすため半径に足した部分
rad += 20 * np.sin(height/LAYER*np.pi)
を
rad += 20 * np.sin(z/0.7/LAYER*np.pi)
に修正します.
heightは一層ずつ離散的に増えていく値ですが,z/0.7は第一層目から第二層目まで203段階で連続的に増えていく量です.これをもちいて膨らみ量を計算すると綺麗に連続したラインが得られます.
radでzを参照するよりも前の部分にzの計算式を置いてあげてください.
以上により,完成したスパイラルのコードが以下です.
import numpy as np
import math
from print_functions import *
'''
NOZZLE = 0.8
LAYER = 0.7
Print_speed = 700
Ext_multiplier = 1.4
'''
LAYER=100
base_rad = 50
def object_modeling():
full_object=[]
for height in range(LAYER):
arg = np.linspace(0, np.pi*2,203)
amp = 2
z = np.linspace(height*0.7, (height+1)*0.7, 203)
rad = base_rad + amp*np.sin(arg*50.5+np.pi*height)
rad += 20 * np.sin(z/0.7/LAYER*np.pi)
x = rad*np.cos(arg )
y = rad*np.sin(arg )
wave_wall = print_layer(x, y, z)
full_object.append(wave_wall)
return full_object
プレビューではほとんど変わりませんが,実際に印刷してみると,縦に入っていたシームが綺麗に消え去り,非常に綺麗な質感になります.
ここまでで,本質的な編み形状に関する記述は終わりです.
底面をつける
以下のスクリプトを実行すると,底面をつけることができます.
import numpy as np
import math
from print_functions import *
'''
NOZZLE = 0.8
LAYER = 0.7
Print_speed = 700
Ext_multiplier = 1.4
'''
LAYER=100
base_rad = 50
def object_modeling():
full_object=[]
for height in range(LAYER):
arg = np.linspace(0, np.pi*2,203)
amp = 2
z = np.linspace(height*0.7, (height+1)*0.7, 203)
rad = base_rad+amp*np.sin(arg*50.5+np.pi*height)
rad += 20 * np.sin(z/0.7/LAYER*np.pi)
x = rad*np.cos(arg )
y = rad*np.sin(arg )
wave_wall = print_layer(x, y, z)
full_object.append(wave_wall)
if height <2:
#内側の円
arg = np.linspace(0, np.pi*2,401)
rad = base_rad-2
x = rad*np.cos(arg )
y = rad*np.sin(arg )
z = np.full_like(arg, height*0.7+0.7)
inner_wall = print_layer(x, y, z,Feed = 1000)
full_object.append(inner_wall)
#底面の格子
arg = np.linspace(0, np.pi*2,401)
rad = base_rad-2-0.5
x = rad*np.cos(arg )
y = rad*np.sin(arg )
z = np.full_like(arg, height*0.7+0.7)
layer_pos = np.column_stack([x, y, z])
infill = line_fill(layer_pos,2.5,np.pi/4*(-1)**height)
bottom = print_layer(infill[0], infill[1], infill[2],Feed = 1000)
full_object.append(bottom)
#(0,0,10)にトラベル
x = 0
y = 0
z = 10
travel_point = print_layer(x, y, z)
full_object.append(travel_point)
return full_object
第0層目と第1層目の二つで底面を印刷します.
記事がかなり長くなってしまったので,細かい内容に関してはまた,別の記事にします.
あとは,半径や膨らみ具合など,細かい点を調整すると,最初の画像のようなものが出来上がります.
サンプル

この画像のサンプルを印刷するのに必要なスクリプトを置いておきます.エディターにコピペで使えるはずです.
githubのリポジトリの中のexampleフォルダの中にも同じものが入っています.
import numpy as np
import math
from print_functions import *
'''
NOZZLE = 1
LAYER = 1
Print_speed = 500
Ext_multiplier = 1
'''
LAYER=40
base_rad = 60
def object_modeling():
full_object=[]
for height in range(LAYER):
arg = np.linspace(0, np.pi*2,403)
amp = 2
z = np.linspace(height*1,(height+1)*1,403)
rad = base_rad+amp*np.sin(arg*100.5+np.pi*height)
rad += 7*np.sin((z/LAYER)*np.pi)
x = rad*np.cos(arg )
y = rad*np.sin(arg )
wave_wall = print_layer(x, y, z)
full_object.append(wave_wall)
if height <2:
arg = np.linspace(0, np.pi*2,401)
rad = base_rad-2
x = rad*np.cos(arg )
y = rad*np.sin(arg )
z = np.full_like(arg, height*1+1)
inner_wall = print_layer(x, y, z,Feed = 1000)
full_object.append(inner_wall)
arg = np.linspace(0, np.pi*2,401)
rad = base_rad-2-0.5
x = rad*np.cos(arg )
y = rad*np.sin(arg )
z = np.full_like(arg, height*1+1)
layer_pos = np.column_stack([x, y, z])
infill = line_fill(layer_pos,2.5,np.pi/4*(-1)**height)
bottom = print_layer(infill[0], infill[1], infill[2],Feed = 1000)
full_object.append(bottom)
x = 0
y = 0
z = 10
travel_point = print_layer(x, y, z)
full_object.append(travel_point)
return full_object
印刷設定に関して
ノズル径は太めの方がいいかと思われます.自分は,経験上,ノズルを1mmにして,一層の厚さを1mmにすると,綺麗に印刷することができています.もちろん細いノズルを利用して,もっと細かい編み目にすることもできます.その際には,今回扱った振動の数(50.5)や振幅(amp)等を調整することが必要です.
G-coordinatorでの印刷は細かいところまで自分で設定できる反面,逆にいうと,細かいところまで,機械任せにできないということでもあります.
そのため,どうしても多くのトライアンドエラーが必要になってきます.面倒ではありますが,必要なステップです.
サンプルスクリプトの中に,印刷設定はコメントとして書いてはありますが,あくまで参考程度のものです.お使いのプリンターに合わせて,細かな調整をしてください.
最後に
また,G-coordinator自体まだまだアップデートしていく予定です.上のように,底面をつけるだけで,コードをたくさん書かなくちゃいけないのは,しんどいので,もっと綺麗に実装できるように,関数やモジュールを公開していきます.
実行ファイルを作成するのは,結構手間がかかるので,もし,こうした新しい機能を搭載した最新verが欲しい場合には,githubから随時コードをダウンロードしてください.
メジャーアップデートがあった場合には,mac用,windows用にバイナリを作ります.