sqrt命令とrsqrtsq命令とrsqrteq命令

はじめに

• この記事はひとりNEONアドベントカレンダー2020 13日目の記事です
• 昨日はmls命令を紹介した。
• 今日はdivの記事で少し触れたArm v7での単精度浮動小数点数の割り算と平方根について解説する

• 通常このヘッダ画像には命令群をグループ分けしたツリー構造の図を用いるのだが、今回説明する命令群は、数が少ないので、割愛する。
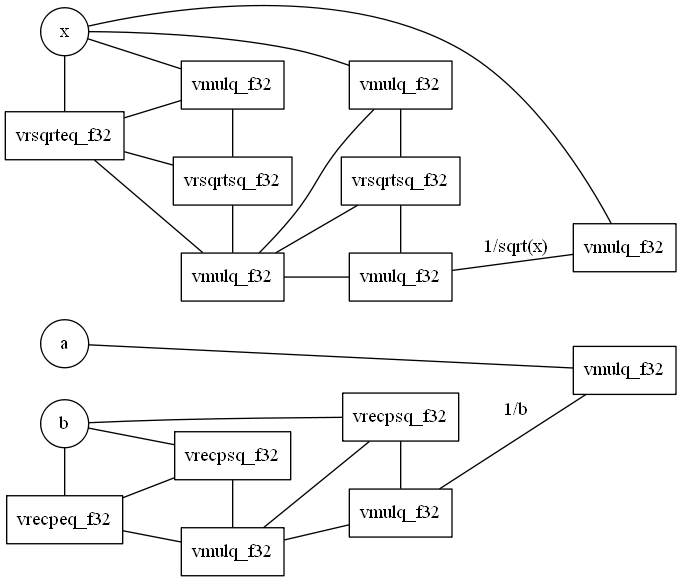
• その代わりに、ニュートン法で逆数と平方根を求める方法を可視化した図をヘッダに使う

Arm v7 にはdiv命令とsqrt命令が無い

• div命令の回で触れたが、Arm v7にはdiv命令が無い。
• これは単純に浮動小数点の割り算は、回路規模が大きくなるため、それをきらったものと思われる。
• しかし、割り算命令は無いものの、省エネで割り算および平方根を求める方法を紹介する
• 早速だが、divの回と同じくOpenCVのUniversal Intrinsic で平方根を計算しているところを見てみよう

sqrt命令の代わり

intrin_neon.hpp

#if CV_SIMD128_64F
inline v_float32x4 v_sqrt(const v_float32x4& x)
{
    return v_float32x4(vsqrtq_f32(x.val));
}

inline v_float32x4 v_invsqrt(const v_float32x4& x)
{
    v_float32x4 one = v_setall_f32(1.0f);
    return one / v_sqrt(x);
}
#else
inline v_float32x4 v_sqrt(const v_float32x4& x)
{
    float32x4_t x1 = vmaxq_f32(x.val, vdupq_n_f32(FLT_MIN));
    float32x4_t e = vrsqrteq_f32(x1);
    e = vmulq_f32(vrsqrtsq_f32(vmulq_f32(x1, e), e), e);
    e = vmulq_f32(vrsqrtsq_f32(vmulq_f32(x1, e), e), e);
    return v_float32x4(vmulq_f32(x.val, e));
}

inline v_float32x4 v_invsqrt(const v_float32x4& x)
{
    float32x4_t e = vrsqrteq_f32(x.val);
    e = vmulq_f32(vrsqrtsq_f32(vmulq_f32(x.val, e), e), e);
    e = vmulq_f32(vrsqrtsq_f32(vmulq_f32(x.val, e), e), e);
    return v_float32x4(e);
}
#endif

• この通り、CV_SIMD128_64Fの有無の違いで全く違うコードをコンパイルすることになる。
• Arm v8の場合は簡単である。CPUに提供されているvsqrtq命令を使うことで平方根が求まる。

    return v_float32x4(vsqrtq_f32(x.val));

• 一方、Arm v7 の場合はどうか。もう1度、OpenCVのコードを見てみよう。

inline v_float32x4 v_sqrt(const v_float32x4& x)
{
    float32x4_t x1 = vmaxq_f32(x.val, vdupq_n_f32(FLT_MIN));
    float32x4_t e = vrsqrteq_f32(x1);
    e = vmulq_f32(vrsqrtsq_f32(vmulq_f32(x1, e), e), e);
    e = vmulq_f32(vrsqrtsq_f32(vmulq_f32(x1, e), e), e);
    return v_float32x4(vmulq_f32(x.val, e));
}

• 関数内最初のvmaxqは、負数を取り除くためにFLT_MINとの最大値を取っている。
• 本質は2行目のvrsqrteq_f32命令と、3、4行目に現れるvrsqrtsq_f32命令である。
• 同じ命令に見えて vrsqrt"e"q_f32 と vrsqrt"s"q_f32 で、1文字だけ違う。
• 数値的にはニュートン法で近似を求め、それを近似を近づける操作を繰り返している。
• 最初の近似は vrsqrteq_f32で求める。¹
• これで近似が求まるが、精度は随分低い。ちなみに、近似は$\sqrt{x}$ではなく$\frac{1}{\sqrt{x}}$を求める。
• で、結果をもとの数と掛け合わせた積が、1に近づくようにどんどん近似していく。
  • floatの分解能を満たすためには、2周改善すると実用上十分近似できる。

div命令の代わり

• div命令の代わりも同じである

inline v_float32x4 operator / (const v_float32x4& a, const v_float32x4& b)
{
    float32x4_t reciprocal = vrecpeq_f32(b.val);
    reciprocal = vmulq_f32(vrecpsq_f32(b.val, reciprocal), reciprocal);
    reciprocal = vmulq_f32(vrecpsq_f32(b.val, reciprocal), reciprocal);
    return v_float32x4(vmulq_f32(a.val, reciprocal));
}
inline v_float32x4& operator /= (v_float32x4& a, const v_float32x4& b)
{
    float32x4_t reciprocal = vrecpeq_f32(b.val);
    reciprocal = vmulq_f32(vrecpsq_f32(b.val, reciprocal), reciprocal);
    reciprocal = vmulq_f32(vrecpsq_f32(b.val, reciprocal), reciprocal);
    a.val = vmulq_f32(a.val, reciprocal);
    return a;
}

• vrecpeq_f32命令で初期値を推定し、vrecpsq_f32命令とvmulq_f32の組み合わせで$1 / x$を近似する
• 微妙にIEEE754準拠ではないが、実用的な精度は出る。

$ grep ^vrsqrt[se]q /usr/lib/gcc/aarch64-linux-gnu/7.5.0/include/arm_neon.h 
vrsqrteq_u32 (uint32x4_t a)
vrsqrteq_f32 (float32x4_t __a)
vrsqrteq_f64 (float64x2_t __a)
vrsqrtsq_f32 (float32x4_t __a, float32x4_t __b)
vrsqrtsq_f64 (float64x2_t __a, float64x2_t __b)
vrsqrteq_f16 (float16x8_t a)
vrsqrtsq_f16 (float16x8_t a, float16x8_t b)

おわりに

• 本記事の途中でも、divの記事でも書いたが、ArmのCPUはもともと組み込み向け用途だった
• なので、こういう命令のサポート状況に、「組み込み由来」である名残を確認できる。
• 明日も手島の執筆の予定で、bit演算子命令を紹介する予定

1. 余談だけど、多分意味は vがベクトル、rが反復を意味するreciprocal、sqrtが平方根、eがestimte、sがstepを意味すると想像する ↩