mls -積差命令-

はじめに

• この記事はひとりNEONアドベントカレンダー2020 12日目の記事です
• 昨日はmla命令を紹介した。
• 今日はmls積差命令を紹介する ネタ切れって言わないでね！

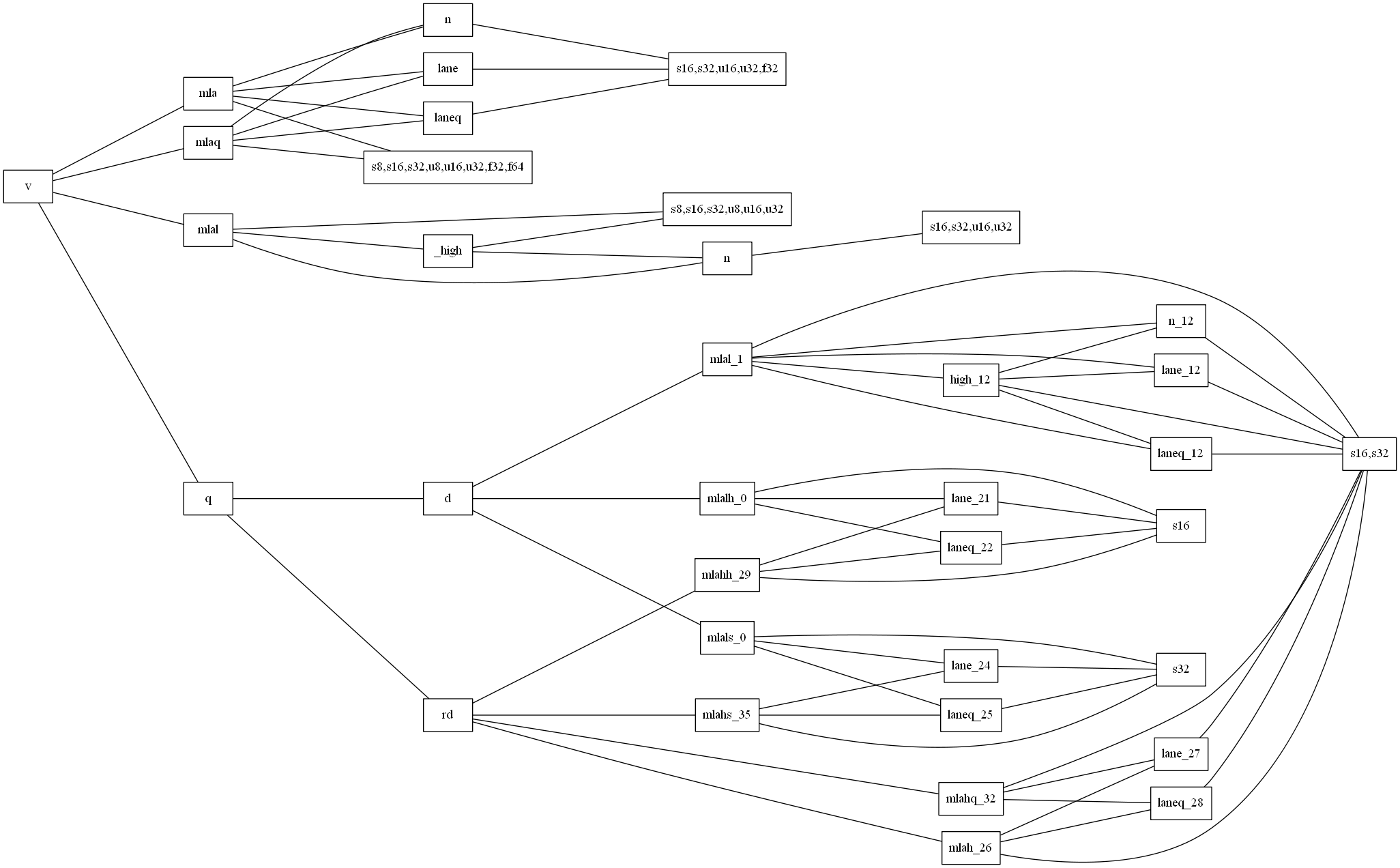
$ grep '^v.*mls' /usr/lib/gcc/aarch64-linux-gnu/7.5.0/include/arm_neon.h | cut -f 1 -d ' ' | sed -e 's/_[sufp][0-9]\+//g' | sort | uniq -c
      8 vmls
      5 vmls_lane
      5 vmls_laneq
      5 vmls_n
      6 vmlsl
      6 vmlsl_high
      4 vmlsl_high_n
      4 vmlsl_n
      8 vmlsq
      5 vmlsq_lane
      5 vmlsq_laneq
      5 vmlsq_n
      2 vqdmlsl
      2 vqdmlsl_high
      2 vqdmlsl_high_lane
      2 vqdmlsl_high_laneq
      2 vqdmlsl_high_n
      2 vqdmlsl_lane
      2 vqdmlsl_laneq
      2 vqdmlsl_n
      1 vqdmlslh
      1 vqdmlslh_lane
      1 vqdmlslh_laneq
      1 vqdmlsls
      1 vqdmlsls_lane
      1 vqdmlsls_laneq
      2 vqrdmlsh
      2 vqrdmlsh_lane
      2 vqrdmlsh_laneq
      1 vqrdmlshh
      1 vqrdmlshh_lane
      1 vqrdmlshh_laneq
      2 vqrdmlshq
      2 vqrdmlshq_lane
      2 vqrdmlshq_laneq
      1 vqrdmlshs
      1 vqrdmlshs_lane
      1 vqrdmlshs_laneq

vmls、vmlsq

• 3つの引数a、b、cを取り、各ベクトル内の要素ごとに、a - b * cを計算する。
• vmlsが64bit幅、vmlsqが128bit幅用命令
• mla命令と同じく、b * cを計算した時点では丸め処理は行われず、桁落ちが起きにくいようになっている。

vmls_lane、vmls_laneq

• 3つの引数a、b、cと定数iを取り、各ベクトル内の要素ごとに、a - b * c[i]を計算する。
• iはコンパイル時定数の必要あり
  • 当然範囲外の即値を指定するとコンパイルできない。

vqdmlsl

• 3つの引数a、b、cを取るのは他の命令と同じ。
• この命令は整数型しか存在せず、浮動小数点型の命令は存在しない。
• a、b、cの型の組み合わせは以下の2つ
  • int32x4_t vqdmlsl(int32x4_t a, int16x4_t b, int16x4_t c)
  • int64x2_t vqdmlsl(int64x2_t a, int32x2_t b, int32x2_t c)
  • aのデータ型とb、cのデータ型が違うだけでなく、bit幅が64/128で違う点も特徴である。
  • これはb*cの乗算がオーバーフローする場合に備えて、より広い幅のデータ型に乗算結果を格納し、オーバーフローを防ぐ命令である。

vqrdmlsh

• だんだんよくわからなくなってくるが、arm_neon.hでの宣言を見てみてよう

$ grep -e '^v.*mls' -e rdma -e pop /usr/lib/gcc/aarch64-linux-gnu/7.5.0/include/arm_neon.h
 : 
#pragma GCC target ("+nothing+rdma")
vqrdmlsh_s16 (int16x4_t __a, int16x4_t __b, int16x4_t __c)
vqrdmlsh_s32 (int32x2_t __a, int32x2_t __b, int32x2_t __c)
vqrdmlshq_s16 (int16x8_t __a, int16x8_t __b, int16x8_t __c)
vqrdmlshq_s32 (int32x4_t __a, int32x4_t __b, int32x4_t __c)
vqrdmlsh_laneq_s16 (int16x4_t __a, int16x4_t __b, int16x8_t __c, const int __d)
vqrdmlsh_laneq_s32 (int32x2_t __a, int32x2_t __b, int32x4_t __c, const int __d)
vqrdmlshq_laneq_s16 (int16x8_t __a, int16x8_t __b, int16x8_t __c, const int __d)
vqrdmlshq_laneq_s32 (int32x4_t __a, int32x4_t __b, int32x4_t __c, const int __d)
vqrdmlsh_lane_s16 (int16x4_t __a, int16x4_t __b, int16x4_t __c, const int __d)
vqrdmlsh_lane_s32 (int32x2_t __a, int32x2_t __b, int32x2_t __c, const int __d)
vqrdmlshq_lane_s16 (int16x8_t __a, int16x8_t __b, int16x4_t __c, const int __d)
vqrdmlshq_lane_s32 (int32x4_t __a, int32x4_t __b, int32x2_t __c, const int __d)
vqrdmlshh_s16 (int16_t __a, int16_t __b, int16_t __c)
vqrdmlshh_lane_s16 (int16_t __a, int16_t __b, int16x4_t __c, const int __d)
vqrdmlshh_laneq_s16 (int16_t __a, int16_t __b, int16x8_t __c, const int __d)
vqrdmlshs_s32 (int32_t __a, int32_t __b, int32_t __c)
vqrdmlshs_lane_s32 (int32_t __a, int32_t __b, int32x2_t __c, const int __d)
vqrdmlshs_laneq_s32 (int32_t __a, int32_t __b, int32x4_t __c, const int __d)
#pragma GCC pop_options

• 実際に試して挙動を試してみようとしたが、vqrdmlsh はv8.1準拠命令だった
• 手持ちのボードでv8.1拡張命令に対応しているやつらはいなかったので、残念ながら挙動を試せなかった。

arm_neon.hpp

/* ARMv8.1-A instrinsics.  */
#pragma GCC push_options
#pragma GCC target ("+nothing+rdma")

__extension__ extern __inline int16x4_t
__attribute__ ((__always_inline__, __gnu_inline__, __artificial__))
vqrdmlah_s16 (int16x4_t __a, int16x4_t __b, int16x4_t __c)
{
  return __builtin_aarch64_sqrdmlahv4hi (__a, __b, __c);
}

:
vqrdmlshs_laneq_s32 (int32_t __a, int32_t __b, int32x4_t __c, const int __d)
{
  return __builtin_aarch64_sqrdmlsh_laneqsi (__a, __b, __c, __d);
}
#pragma GCC pop_options

おわりに

• ~~ネタ切れ感が出てきたけれど、~~あと2週間がんばります
• 明日はdiv命令のときの記事で予告した、Arm v7 で単精度浮動小数点数の割り算と平方根を計算する命令を紹介する予定