mla -積和命令-

はじめに

• この記事はひとりNEONアドベントカレンダー2020 11日目の記事です
• 昨日はstore命令を紹介した。
• みんな大好き積和命令を紹介する

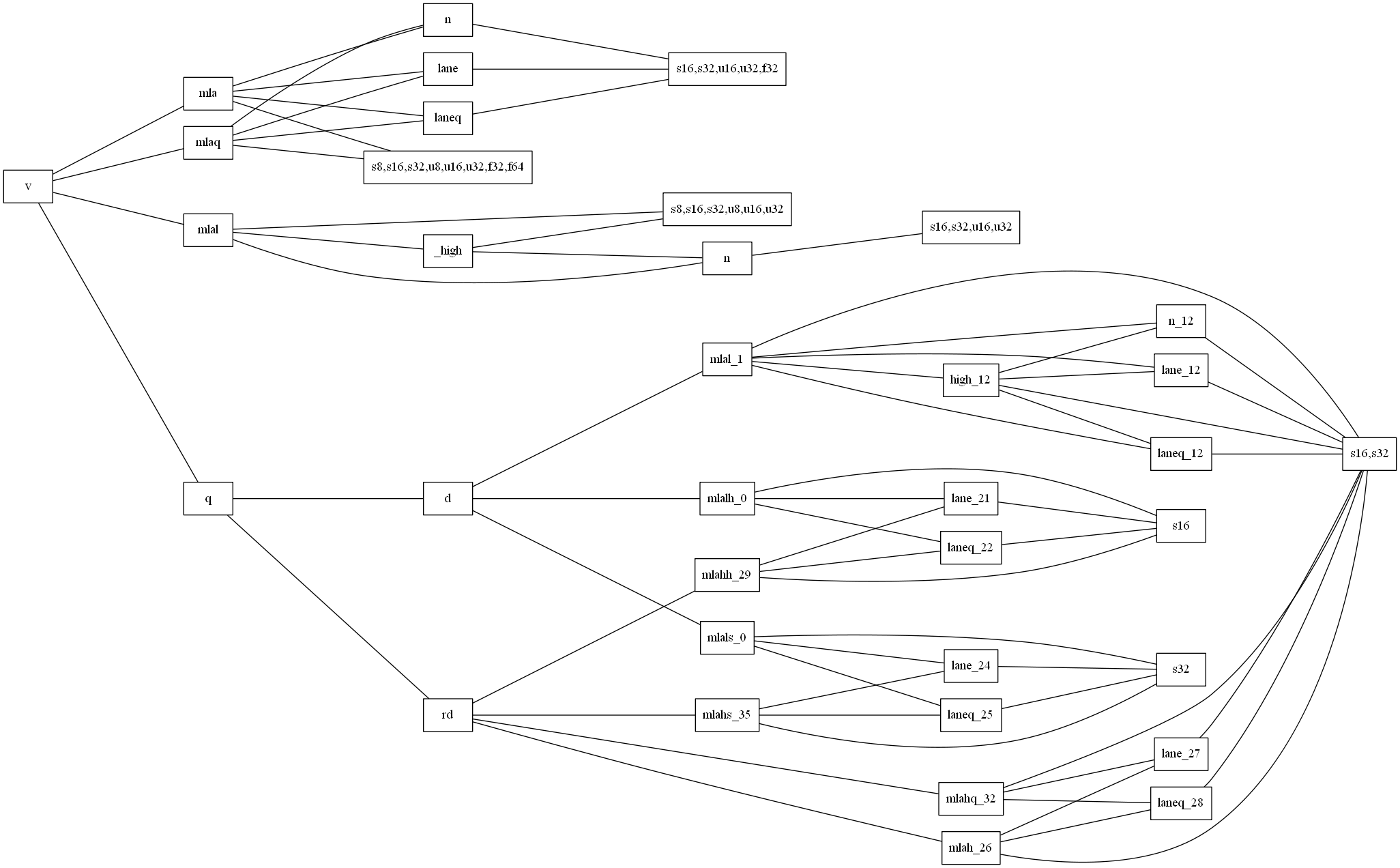
$ grep ^v.*mla /usr/lib/gcc/aarch64-linux-gnu/7.5.0/include/arm_neon.h | cut -f 1 -d ' ' | sed -e 's/[suf][0-9]\+//g' | sort | uniq -c
      8 vmla_
      5 vmla_lane_
      5 vmla_laneq_
      5 vmla_n_
      6 vmlal_
      6 vmlal_high_
      4 vmlal_high_n_
      4 vmlal_n_
      8 vmlaq_
      5 vmlaq_lane_
      5 vmlaq_laneq_
      5 vmlaq_n_
      2 vqdmlal_
      2 vqdmlal_high_
      2 vqdmlal_high_lane_
      2 vqdmlal_high_laneq_
      2 vqdmlal_high_n_
      2 vqdmlal_lane_
      2 vqdmlal_laneq_
      2 vqdmlal_n_
      1 vqdmlalh_
      1 vqdmlalh_lane_
      1 vqdmlalh_laneq_
      1 vqdmlals_
      1 vqdmlals_lane_
      1 vqdmlals_laneq_
      2 vqrdmlah_
      2 vqrdmlah_lane_
      2 vqrdmlah_laneq_
      1 vqrdmlahh_
      1 vqrdmlahh_lane_
      1 vqrdmlahh_laneq_
      2 vqrdmlahq_
      2 vqrdmlahq_lane_
      2 vqrdmlahq_laneq_
      1 vqrdmlahs_
      1 vqrdmlahs_lane_
      1 vqrdmlahs_laneq_

mla命令

• 積和命令は、mlaとmlaqが基本形で、a、b、cの3パラメータを受け取り、a + b * cを返す
• mla_n、mla_lane、mla_laneqは、cがベクトルでなく、1つの値(ベクトルの中のレーンで指定したり、単一のintで指定したりする)
• mlalは、入力のレーン数を半減する代わりに、乗算結果がオーバーフローしないように引数b``cのbit拡張を行う
  • mlalは下位半分のレーンを利用し、mlal_highは上位半分のレーンを使う
  • mlal_nとmlal_high_nはbの半分のレーンを使い、cはベクトルでなく単一の値を使う
• vqdmla命令はa+b*cでなく、a+b*c*2を計算する。
• vqrdmla命令はa+b*cでなく、a+b*c*2+(const)を計算する。

vqdmlal

vqdmlal.cpp

#include <arm_neon.h>
#include <iostream>


#define KERNEL(suffix1, suffix2, nSize, type1, type2, vtype1, vtype2) \
void kernel_##suffix1()                                               \
{                                                                     \
        type1 src0[] = { 198, 207,  51, 984};                         \
        type1 src1[] = { 122, 920, 151, 129};                         \
        type2 acc [] = { 10000, 10000, 10000, 10000, };               \
        type2 res [] = {   0,   0,   0,   0};                         \
        int ## vtype2 ## _t a = vld1q_## suffix2(acc);                \
        int ## vtype1 ## _t b = vld1_## suffix1(src0);                \
        int ## vtype1 ## _t c = vld1_## suffix1(src1);                \
        int ## vtype2 ## _t d = vqdmlal_## suffix1(a, b, c);          \
        vst1q_ ## suffix2(res, d);                                    \
        for( auto i = 0;i < nSize;i++)                                \
        {                                                             \
            std::cout << i << ":" << acc[i] << '\t' << src0[i] << '\t' << src1[i] << '\t' << res[i] << std::endl;  \
        }                                                             \
}

KERNEL(s32, s64, 2, int,   int64_t, 32x2, 64x2);
KERNEL(s16, s32, 4, short, int,     16x4, 32x4);

int main(int argc, char** argv)
{
        kernel_s32();
        kernel_s16();
}

0:10000 198     122     58312
1:10000 207     920     390880
0:10000 198     122     58312
1:10000 207     920     390880
2:10000 51      151     25402
3:10000 984     129     263872

• a + b * c * 2が実行される。b*c*2はオーバーフローに備えて乗算前に符号拡張される。vqが接頭辞なので、最後の加算は飽和演算。
  接頭辞が純粋にvだけの非飽和演算は存在しない。

vqdmlalh vqdmlals

v q d mla l なので、ベクトル演算、飽和演算、倍加算、積和演算、bit拡張。最後のh``sは、half word(16bit)single word(32bit)に対応する接尾辞で、_s16、_s32に相当する。vが接頭辞だが、単体の a + b * c * 2しか行わない。つまり、厳密にはSIMD命令では無い。

vqrdmlah

• v8.1拡張命令

arm_neon.h

#pragma GCC target ("+nothing+rdma")
vqrdmlah_s16 (int16x4_t __a, int16x4_t __b, int16x4_t __c)
vqrdmlah_s32 (int32x2_t __a, int32x2_t __b, int32x2_t __c)
vqrdmlahq_s16 (int16x8_t __a, int16x8_t __b, int16x8_t __c)
vqrdmlahq_s32 (int32x4_t __a, int32x4_t __b, int32x4_t __c)
vqrdmlah_laneq_s16 (int16x4_t __a, int16x4_t __b, int16x8_t __c, const int __d)
vqrdmlah_laneq_s32 (int32x2_t __a, int32x2_t __b, int32x4_t __c, const int __d)
vqrdmlahq_laneq_s16 (int16x8_t __a, int16x8_t __b, int16x8_t __c, const int __d)
vqrdmlahq_laneq_s32 (int32x4_t __a, int32x4_t __b, int32x4_t __c, const int __d)
vqrdmlah_lane_s16 (int16x4_t __a, int16x4_t __b, int16x4_t __c, const int __d)
vqrdmlah_lane_s32 (int32x2_t __a, int32x2_t __b, int32x2_t __c, const int __d)
vqrdmlahq_lane_s16 (int16x8_t __a, int16x8_t __b, int16x4_t __c, const int __d)
vqrdmlahq_lane_s32 (int32x4_t __a, int32x4_t __b, int32x2_t __c, const int __d)
vqrdmlahh_s16 (int16_t __a, int16_t __b, int16_t __c)
vqrdmlahh_lane_s16 (int16_t __a, int16_t __b, int16x4_t __c, const int __d)
vqrdmlahh_laneq_s16 (int16_t __a, int16_t __b, int16x8_t __c, const int __d)
vqrdmlahs_s32 (int32_t __a, int32_t __b, int32_t __c)
vqrdmlahs_lane_s32 (int32_t __a, int32_t __b, int32x2_t __c, const int __d)
vqrdmlahs_laneq_s32 (int32_t __a, int32_t __b, int32x4_t __c, const int __d)
#pragma GCC pop_options

fma命令

• 浮動小数点型向けには、fma命令も提供される

$ grep ^vfma /usr/lib/gcc/aarch64-linux-gnu/7.5.0/include/arm_neon.h
vfma_f64 (float64x1_t __a, float64x1_t __b, float64x1_t __c)
vfma_f32 (float32x2_t __a, float32x2_t __b, float32x2_t __c)
vfmaq_f32 (float32x4_t __a, float32x4_t __b, float32x4_t __c)
vfmaq_f64 (float64x2_t __a, float64x2_t __b, float64x2_t __c)
vfma_n_f32 (float32x2_t __a, float32x2_t __b, float32_t __c)
vfma_n_f64 (float64x1_t __a, float64x1_t __b, float64_t __c)
vfmaq_n_f32 (float32x4_t __a, float32x4_t __b, float32_t __c)
vfmaq_n_f64 (float64x2_t __a, float64x2_t __b, float64_t __c)
vfma_lane_f32 (float32x2_t __a, float32x2_t __b,
vfma_lane_f64 (float64x1_t __a, float64x1_t __b,
vfmad_lane_f64 (float64_t __a, float64_t __b,
vfmas_lane_f32 (float32_t __a, float32_t __b,
vfma_laneq_f32 (float32x2_t __a, float32x2_t __b,
vfma_laneq_f64 (float64x1_t __a, float64x1_t __b,
vfmad_laneq_f64 (float64_t __a, float64_t __b,
vfmas_laneq_f32 (float32_t __a, float32_t __b,
vfmaq_lane_f32 (float32x4_t __a, float32x4_t __b,
vfmaq_lane_f64 (float64x2_t __a, float64x2_t __b,
vfmaq_laneq_f32 (float32x4_t __a, float32x4_t __b,
vfmaq_laneq_f64 (float64x2_t __a, float64x2_t __b,
vfma_f16 (float16x4_t __a, float16x4_t __b, float16x4_t __c)
vfmaq_f16 (float16x8_t __a, float16x8_t __b, float16x8_t __c)
vfmah_lane_f16 (float16_t __a, float16_t __b,
vfmah_laneq_f16 (float16_t __a, float16_t __b,
vfma_lane_f16 (float16x4_t __a, float16x4_t __b,
vfmaq_lane_f16 (float16x8_t __a, float16x8_t __b,
vfma_laneq_f16 (float16x4_t __a, float16x4_t __b,
vfmaq_laneq_f16 (float16x8_t __a, float16x8_t __b,
vfma_n_f16 (float16x4_t __a, float16x4_t __b, float16_t __c)
vfmaq_n_f16 (float16x8_t __a, float16x8_t __b, float16_t __c)

• しかし、謎にmla命令も浮動小数点型向けに提供される

$ grep ^vmla.*_f /usr/lib/gcc/aarch64-linux-gnu/7.5.0/include/arm_neon.h
vmla_n_f32 (float32x2_t a, float32x2_t b, float32_t c)
vmlaq_n_f32 (float32x4_t a, float32x4_t b, float32_t c)
vmla_f32 (float32x2_t a, float32x2_t b, float32x2_t c)
vmla_f64 (float64x1_t __a, float64x1_t __b, float64x1_t __c)
vmlaq_f32 (float32x4_t a, float32x4_t b, float32x4_t c)
vmlaq_f64 (float64x2_t a, float64x2_t b, float64x2_t c)
vmla_lane_f32 (float32x2_t __a, float32x2_t __b,
vmla_laneq_f32 (float32x2_t __a, float32x2_t __b,
vmlaq_lane_f32 (float32x4_t __a, float32x4_t __b,
vmlaq_laneq_f32 (float32x4_t __a, float32x4_t __b,

• ん？じゃあmlaq_f32とfmaq_f32の違いは？
• mlaq_f32とfmaq_f32の公式ドキュメントを見ると
• mlaq_f32

Floating-point multiply-add to accumulator

• fmaq_f32

Floating-point fused multiply-add to accumulator

• となっている。一応arm_neon.hも見てみよう

arm_neon.h

vmlaq_f32 (float32x4_t a, float32x4_t b, float32x4_t c)
{
  return a + b * c;
}
:
vfmaq_f32 (float32x4_t __a, float32x4_t __b, float32x4_t __c)
{
  return __builtin_aarch64_fmav4sf (__b, __c, __a);
}

• なるほど、解説の通り、mla命令は本当にただ掛けて足しているだけである
• 一方でfma命令はfmav4sfというビルトイン関数を呼んでおり、こちらはたしかにfusedされてそうである。
• 実際にサンプルコードで試してみよう

mla.cpp

union suf32
{
        int32_t s;
        uint32_t u;
        float f;
};

void dumpHex(float32x4_t& v)
{
        float work[4];
        vst1q_f32(work, v);
        for(int i = 0;i < 4;i++)
        {
                suf32 conv;
                conv.f = work[i];
                std::cout << i << "\t0x" << std::hex << conv.u << '\t' << conv.f << std::endl;
        }
}

int main(int argc, char**argv)
{
    float src0[] = {-10703290.9296708,-10703290.9296708,-10703290.9296708,-10703290.9296708,};
    float src1[] = {3333.3333, 3333.3333, 3333.3333, 3333.3333,};
    float src2[] = {3210.9876, 3210.9876, 3210.9876, 3210.9876,};
    float32x4_t vsrc0 = vld1q_f32(src0);
    float32x4_t vsrc1 = vld1q_f32(src1);
    float32x4_t vsrc2 = vld1q_f32(src2);
    {
            float32x4_t v_dst = vmlaq_f32(vsrc0, vsrc1, vsrc2); // vsrc0 + vsrc1 * vsrc2
            dumpHex(v_dst);
    }
    {
            float32x4_t v_dst = vfmaq_f32(vsrc0, vsrc1, vsrc2); // vsrc0 + vsrc1 * vsrc2
            dumpHex(v_dst);
    }
    return 0;
}

• このコードは、fusedされてるどうかを判定するために、両方のintrinsicを利用する
  • また、fusedされてる場合は桁落ちしないが、ただ掛けて足すだけだと桁落ちが発生する。
  • 桁落ちを再現するために、積は$3333.3333 \times 3210.9876 = 10703291.89296708$、積和の結果は$0.96329628$と、 積に対して演算結果が非常に小さくなるように設定した
  • 通常のfloatの演算では、桁落ちが発生し、結果が一致しない。
  • fusedされてる場合は途中の積が丸められないため、小さい桁まで保持される
• では実際に実行してみよう
• 結論から先に書くと、最適化レベルに応じてmla命令の挙動が変わったが、fma命令の挙動は変わらなかった。
• その点は注意が必要である（なお、GCC 7.5.0で確認)
• 最適化レベル-O2

0       0x3f117011      0.568116    // mlaの結果
1       0x3f117011      0.568116    // mlaの結果
2       0x3f117011      0.568116    // mlaの結果
3       0x3f117011      0.568116    // mlaの結果
0       0x3f117011      0.568116    // fmaの結果
1       0x3f117011      0.568116    // fmaの結果
2       0x3f117011      0.568116    // fmaの結果
3       0x3f117011      0.568116    // fmaの結果

• 最適化レベル-O1

0       0x3f800000      1           // mlaの結果
1       0x3f800000      1           // mlaの結果
2       0x3f800000      1           // mlaの結果
3       0x3f800000      1           // mlaの結果
0       0x3f117011      0.568116    // fmaの結果
1       0x3f117011      0.568116    // fmaの結果
2       0x3f117011      0.568116    // fmaの結果
3       0x3f117011      0.568116    // fmaの結果

• 10進数表記と16進数表記を併記した。
• 最適化レベル-O2では、mlaの結果とfmaの結果はbit-exactである。
• 一方で、-O1ではmlaとfmaはピッタリは一致しない。mlaの結果の、下位bitが多数0になっている
  • これが桁落ちと呼ばれる現象
• という訳で
  • mla命令は掛けて足すだけ（ただしコンパイラによっては最適化によってfusedされることがある
  • fma命令はかならずfusedされる
  • ことが分かった

おわりに

• 積和命令を紹介した
• 明日も手島の執筆の予定ですが、そろそろネタが尽きるので、明日は何を書くか未定です