はじめに
因果と相関は違う、というのは使い古された言葉かもしれません。
因果と相関の問題は、データ分析をしようとすると、必ず直面するのではないでしょうか。
今回は、どんな因果関係があるときに二つの変数間に相関が発生するかを考えたます。
そののち、やや複雑な因果関係がある場合に、因果の効果を推定する方法を解説します。
相関が発生する因果関係
二つの変数AとBに相関(負の相関含む)があるとしましょう。これにはいくつかの場合が考えられます。
1)AからBに因果関係がある
一番自明なのはこれですね。
例えば、野球選手の打率と年俸には相関があるでしょう。
この2つの変数の間には、打率が高いほど年俸が高くなる、という因果関係が存在しますね。逆に、年俸を上げたから打率が高くなるわけではないというのも、感覚的に自明ではないでしょうか。
2)AとBに共通原因となる別の変数Cからの因果関係がある
例えば有名な例ですが、アイスクリームがよく売れる日には犯罪が多く発生するそうです。
これはアイスクリームを食べると人間を衝動的に犯罪に突き動かすわけでも、犯罪者が頭を冷やすためにアイスクリームを食べるわけでもありません。
気温が高いとアイスクリームがよく売れ、同時に高い気温は人間の暴力性を増すそうです。
つまり、アイスクリームの売上と犯罪発生件数という二つの変数は、ともに気温という別の変数から因果を受けているため、相関が生まれているのです。
3)AとBの両方から因果を受けた別の変数Dでバイアスされている
これは少しややこしいですね。例えば、英語と数学の2科目受験で入れる中堅大学の現学生の入試での成績を考えてみましょう。本来、学生の英語と数学の点数は独立に決まる(=相関がない)とします。
簡単のため、両科目100点満点ずつで、合計点が120点が合格点だったとします。
すると、学生の英語の点数と数学の点数の和が120点を下回る場合には、その大学に入学できていないため、分母に含まれません。一方、とても良い点を取れる学生(たとえば180点)もより上位の大学に進学してしまうため、母数に入ってきません。
その結果、観測されるのは(数学)+(英語)が高すぎず低すぎずの学生たちです。
横軸に数学、縦軸に英語の散布図を考えると、この学生たちは左上(すごく英語が得意だが数学が大苦手)から右下(その逆)に向かう帯状に分布します。つまり、数学と英語の能力には負の相関が生まれてしまうのです。
これはなぜかと振り返って考えてみると、合計点でバイアス(フィルター)した結果、本来なかった相関があるように観測されたのでした。
因果効果の推定
簡単な例
変数Aを「人工的に」変えることができたときに、変数Bがどれくらい変わるかを、因果効果と呼びます。
例えば上の例で、安売りなどでアイスクリームをもっとたくさん売ることができたとしましょう。その時、犯罪発生件数は変わるでしょうか?アイスクリームの売上から犯罪発生件数への因果はないので、この時の因果効果は0です。
一方、野球選手の打率が0.020改善した場合、年俸は変わるのでしょうか?打率から年俸への因果関係があるので、年俸は変わる(おそらく上がる)と予想されます。このとき、「どれくらい」年俸が上がるかを考えるのが因果効果の推定です。
この場合、(もっともシンプルには、)年俸を打率で回帰してその係数を見てあげれば、打率が0.020あがった時の年俸への影響を知ることができます。
複雑な例
物事が複雑になるのは、変数Aと変数Bの間の相関が、上記1-3の中の複数の要因が合わさって生まれてきている場合です。例えば次のような例を考えましょう。
あなたはスマホゲーム(ソシャゲ)企業の社員として、ゲーム内のイベントの立案に従事しています。
会社の主力商品である「軍艦これくしょん」(仮名)により課金してもらうため、あなたは高難易度ステージを実装しました。
データを見て、高難易度ステージに挑戦したユーザーと挑戦していないユーザーの平均課金額を比べると、挑戦したユーザーの方が課金額が多いため、あなたは「このステージ実装は成功した」と上司に報告しました。
しかし上司から「もともと課金をしやすいヘビーユーザーが新ステージに挑戦しただけではないのか」と質問されてしました。
あなたはどのようにすれば新ステージの実装が課金を増やしたということができるでしょうか。
状況を整理しましょう。この話には以下の3つの変数が登場します。
X: 新ステージの挑戦への有無 (X=1だと挑戦した、X=0だと挑戦していない)
Y: 課金額
Z: ゲームへの熱心さ(過去3か月のプレイ時間で測るとしましょう)
あなたはXからYへの因果効果を測定したいのですが、XとYはアイスクリームの例のように、Zから因果を受けています。
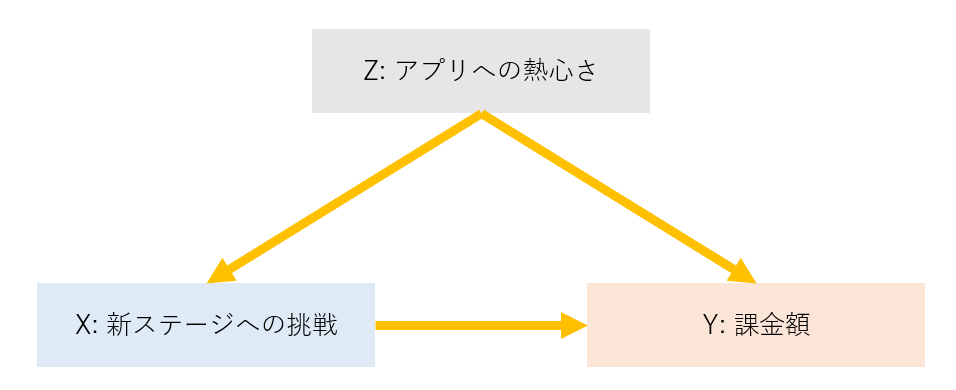
専門的には、このときXからYへの因果には__バックドアパスがある__と言います。平たく言うと、XとYの相関は、XからYへ直接向かう道以外の裏口(バックドア)でもつながってしまっているということです。
この場合、Zが存在するせいでXとYには__XからYへの因果とは無関係に__相関があります。そのために、XからYへの因果効果を測定することが困難になっています。
そのため、XとYの相関だけ、つまり「高難易度ステージに挑戦したユーザーと挑戦していないユーザーの平均課金額を比べると、挑戦したユーザーの方が課金額が多い」ことだけからXからYへの因果を論じることができなくなっているのです。
では、どうすればXからYへの因果効果を測定すればよいのでしょうか。
回帰を使った方法
今回測定したい因果効果は、新ステージをプレイした人としていない人を比べてもわからないということを先ほど述べました。
では因果効果とは何かということを改めて考えてみると、もし新ステージをプレイしていない人がプレイしていたらいくら追加で課金していたか、もしくは逆に__新ステージをプレイした人がプレイしていなかったら、課金はいくら少なくなっていたか__です。これは現実に起こっていないことを仮定しているので__反実仮想__とよびます。
最もシンプルな方法は線形回帰を使うことです。すると、
Y(X,Z) = aX + bZ + c
でYをXとZで表現できます。この係数aがXからYへの因果効果です。
なぜこれはZからの効果を除いたXからYへの因果効果を表しているのでしょう。
簡単に言うと、ZからYへの効果を陽に織り込むことで(係数b)、aは純粋なXからYへの効果を表しているのです。
T-Learner
線形回帰では、すべての人に同じ因果効果を想定していました。しかし実際には個別のユーザーごとに因果効果は異なっているでしょう。それを推定する方法がT-Learnerです。
T-LearnerのTはTwoの頭文字(なぜDoubleのDでないのでしょう・・・)で、文字通り2つのモデルを作って因果効果を推定します。なんの2つかというと、$X=0$と$X=1$のユーザーについて別々のモデルを作ります。
単純のため線形回帰を使うと、
Y(X=0, Z) = b_0 Z + c_0 \\
Y(X=1, Z) = b_1 Z + c_1
となります。そして、因果効果を
a = (b_1 Z + c_1) - Y : X=0 \\
a = Y - (b_0 Z + c_0) : X=1
で推定します。
なにをしているかというと、$X=0$のユーザーには$X=1$のユーザーから作ったモデルを、$X=1$のユーザーには$X=0$のユーザーから作ったモデルを適用して、__もしXが逆だったら__を推定しています。
先ほどとの違いは何かというと、今回はaが個人ごとに異なります。平均的な因果効果を知りたければ、aを全ユーザーで平均すればよいです。
実例
別の記事で食べログの有料会員になることで点数が上がるのか、という検証をしました。
これは、食べログが有料会員を有利にするよう点数を操作しているかの因果分析です。
東京中のラーメンについて、有料会員とそうでない店舗の平均点数を比べると、有料会員が3.41、そうでない店舗が3.36と0.05の差があります。t検定(もう少し厳密な統計検定)してみると、有意に有料会員の点数の方が高くなります。
しかしこれをもって食べログは有料会員に有利な点数操作をしているというのは早計です。
なぜかというと、繁盛しているお店ほどお金に余裕があるので有料会員になりやすいと考えられるからです。つまりアプリの図と全く同じ、
X: 有料会員かどうか
Y: 点数
Z: 店舗の人気度
という因果関係が存在しそうです。
店舗の人気度を測るのは難しいので、食べログへの口コミ数とします。
点数(Y)を口コミ数(Z)と有料会員かどうか(X)で回帰をしてみると、Xの回帰係数は有意になりませんでした。
念のためT-Learnerを(回帰ではなく、非線形な効果にも対応するためランダムフォレストで)試してみても、平均因果効果はほぼ0(むしろややマイナス)となりました。
つまり、有料会員かどうかと点数の相関は、店舗の人気度という共通の原因に由来するもので、直接の因果効果は存在しませんでした。
おわりに
今回は相関が必ずしも因果関係を表していないということを説明し、因果効果を定量的に評価する方法を解説しました。
今回は因果関係の向きがあらかじめわかっている(か、常識的に判断できる)ことを仮定しました。
しかし、因果関係の矢印の向きは常に明らかなわけではありません。
この矢印の向きを機械学習で推論する統計的因果推論という分野も存在するということを最後に記しておきます。