電磁気学を学んだ人がおそらく一回はつまづいたであろうベクトルポテンシャルについて、できるだけ理解しやすいように残しておこうと思います。
電磁波を扱うときは基本的に電界と磁界を使うと思いますが、近年ではベクトルポテンシャルの方が本質ではないかと言われることもしばしばあるので、何が便利かくらいはわかっておきたいですね。
やっぱり登場マクスウェル方程式
こちら、マクスウェル方程式のメンバーです
{\rm div} \boldsymbol{E} = \frac{\rho}{\varepsilon}\\
{\rm div} \boldsymbol{H} = 0\\
{\rm rot} \boldsymbol{H} = \boldsymbol{J}+\varepsilon\frac{\partial\boldsymbol{E}}{\partial t}\\
{\rm rot} \boldsymbol{E} = -\mu\frac{\partial\boldsymbol{H}}{\partial t}
親の顔より見ている気がします。
僕の記事で【FDTD解説シリーズ①】FDTDで電磁界解析基礎というのがあるのですが、FDTDで扱っているのは第3,4式の回転系の式のみです。電場や磁場の湧き出しは設定できず、電場や磁場の初期値を設定するのみでした。
ベクトルポテンシャルは、表現は複雑ですが電磁波の挙動を湧き出しも含めて記述できるものです。これだけでも理解したくなりませんか?なりますよね?なってください。
ベクトル公式
ベクトルポテンシャルを扱う上で必要な演算や公式を紹介します。
ナブラ
ナブラ($\nabla$)はベクトル演算子の一つで、ベクトルとの内積、外積、スカラーとの積をとることができます。
\nabla = \left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)\\
\nabla\cdot\boldsymbol{A} = \left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)\cdot (A_x,A_y,A_z)\\
\nabla\times\boldsymbol{A} = \left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)\times (A_x,A_y,A_z)\\
\nabla\phi = \left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)\phi = \left(\frac{\partial\phi}{\partial x},\frac{\partial\phi}{\partial y},\frac{\partial\phi}{\partial z}\right)
発散
発散は記号で${\rm div}\boldsymbol{A}$もしくは$\nabla\cdot \boldsymbol{A}$と表します。正確にいうとdivを計算したら$\nabla$との内積に等しくなったというものです。ある点からの場の湧き出し量を定量化するものです。
回転
回転も電磁気やってたらわかりますよね。記号は${\rm rot}\boldsymbol{A}$で、計算は$\nabla\times\boldsymbol{A}$と等価です。
公式たち
この記事では以下のベクトル公式を使います。当たり前ですが、この公式たちは変数が何であっても必ず成り立つと言うのが超大事です。
\nabla\cdot(\nabla\times\boldsymbol{A}) = 0
\nabla\times(\nabla\phi) = 0\\
\boldsymbol{X}\times\boldsymbol{Y}\times\boldsymbol{Z} = (\boldsymbol{X}\cdot\boldsymbol{Z})\boldsymbol{Z}-(\boldsymbol{X}\cdot\boldsymbol{Y})\boldsymbol{Z}
ベクトルポテンシャルとスカラーポテンシャル
ベクトルポテンシャルとスカラーポテンシャルの定義は式の上では超簡単で、以下を満たす$\boldsymbol{X}$をベクトルポテンシャル、$\phi$をスカラーポテンシャルと言います。これを導入することで、ナブラとの内積外積をベクトル公式によってゼロにすることができます。
\boldsymbol{Y} = \nabla \times \boldsymbol{X}\\
\boldsymbol{Y} = \nabla\phi
ベクトルポテンシャルとスカラーポテンシャルを定義する目的は、ベクトルの発散や回転をベクトル公式によってゼロにできるからです。都合よくマクスウェル方程式には$\nabla\cdot\boldsymbol{B}=0$の式(アンペールの法則を示している)があるので、磁束密度をベクトルポテンシャルで表しても式の意味を崩しません。
マクスウェルを書き換える
磁束密度をベクトルポテンシャルで表現してみる
まず磁束密度$\boldsymbol{B} = \mu\boldsymbol{H}$について、以下の式で求められる$\boldsymbol{A}$を定めます。
\boldsymbol{B} = \nabla \times \boldsymbol{A}
磁束密度をベクトルとの外積で定義したことで、アンペールの法則に代入すると、ベクトル公式そのものとなって、$\boldsymbol{A}$が何であっても0となります。アンペールの法則は元々「$\boldsymbol{B}$が何であっても磁場の湧き出しはない」を意味するので、意味を崩すことなく書き換えられました。
{\rm div} \boldsymbol{B} = \nabla\cdot(\nabla\times\boldsymbol{A}) = 0\\
アンペールさん、あなたの功績はただのベクトル公式になってしまいました。。。
電場を電磁ポテンシャルで表現してみる
アンペールの法則がベクトルポテンシャルによってベクトル公式と化しました。続いてファラデーの電磁誘導の法則の式に代入します。
{\rm rot} \boldsymbol{E} = -\frac{\partial\boldsymbol{B}}{\partial t} = -\frac{\partial(\nabla \times \boldsymbol{A})}{\partial t} = \nabla\times\left(-\frac{\partial\boldsymbol{A}}{\partial t}\right)\\
${\rm rot}\boldsymbol{E} = \nabla\times\boldsymbol{E}$ですから
\nabla\times\boldsymbol{E} = \nabla\times\left(-\frac{\partial\boldsymbol{A}}{\partial t}\right)\\
\nabla\times\left(\boldsymbol{E} + \frac{\partial\boldsymbol{A}}{\partial t}\right) = 0
となります。回転系のややこしいところがなんだかまとまった気がしますね。これだけでもちょっと感動。
ここで、 $\nabla\times\boldsymbol{X}=0$の形になったので、$\nabla\times(\nabla\phi) = 0$を使うとスカラーポテンシャルが定義できそうです。こうしてみましょう。
\boldsymbol{E} + \frac{\partial\boldsymbol{A}}{\partial t} = -\nabla\phi
$\phi$がスカラーポテンシャルです。これを変形すると、
\boldsymbol{E} = -\nabla\phi - \frac{\partial\boldsymbol{A}}{\partial t}
となります。この$\phi,\boldsymbol{A}$を合わせて電磁ポテンシャルとよびます。
これでマクスウェル方程式のうちアンペールの法則はただのベクトル公式と化し、ファラデーの電磁誘導の法則は電磁ポテンシャルで表現されました。
あと2つの式も電磁ポテンシャルで表現する
電磁ポテンシャルがでたらあとはそれらを他の式にも代入していきます。これは力技です。
{\rm div} \boldsymbol{E} = \frac{\rho}{\varepsilon}\\
\Rightarrow \nabla\cdot\left[-\nabla\phi - \frac{\partial\boldsymbol{A}}{\partial t}\right] = \frac{\rho}{\varepsilon}\\
\Rightarrow -\nabla^2\phi - \nabla\cdot\frac{\partial\boldsymbol{A}}{\partial t} = \frac{\rho}{\varepsilon}\\
\nabla\times\boldsymbol{B} = \mu\boldsymbol{J}+\mu\varepsilon\frac{\partial\boldsymbol{E}}{\partial t}\\
\Rightarrow c^2\nabla\times(\nabla\times\boldsymbol{A}) = \frac{\boldsymbol{J}}{\varepsilon}+\frac{\partial}{\partial t}\left(-\nabla\phi - \frac{\partial\boldsymbol{A}}{\partial t}\right)\\
\Rightarrow c^2(\nabla(\nabla\cdot\boldsymbol{A})-\nabla^2\boldsymbol{A}) = \frac{\boldsymbol{J}}{\varepsilon}+\frac{\partial}{\partial t}\left(-\nabla\phi - \frac{\partial\boldsymbol{A}}{\partial t}\right)
大変でしたが、結果的に電場に関するガウスの法則は電磁ポテンシャルのベクトルポテンシャルとスカラーポテンシャルをリンクさせるような式となり、ストークスの定理は電磁ポテンシャルによって書き変えられました。変形中ファラデーの電磁誘導の法則を代入し、アンペールの法則はベクトル公式と化しているので、この2つの式がマクスウェル方程式と等価な意味を持ちます。式が4つから2つに!!!
ゲージ変換
ここまできて「電場と磁場が決まれば電磁ポテンシャルは一つに決まるのか?もしくはその逆はあるのか?」と疑問に思う人は多分多くないので提唱しておく。式の上ではうまくいっているっぽいけど、ちゃんと電磁場と対応してるのかみてみます。
結果を言うと対応していません。例えば任意のスカラー関数$\chi$を用いたこんなポテンシャルを考えてみましょう。
\boldsymbol{A'} = \boldsymbol{A} + \nabla\chi
紹介したベクトル公式より、$\nabla\times(\nabla\phi) = 0$なので、
\boldsymbol{B} = \nabla\times\boldsymbol{A'} = \nabla\times(\boldsymbol{A} + \nabla\chi) = \nabla\times\boldsymbol{A}
となってしまいます。磁場と電磁ポテンシャルが一意に結びついていないのです。しかし、これを
\boldsymbol{E} = -\nabla\phi - \frac{\partial\boldsymbol{A}}{\partial t}
に代入したとき、時間微分によって電場には$\chi$の影響が出てしまいます。ですが、
$$\phi' = \phi -\frac{\partial\chi}{\partial t}$$
とすることで式の形を崩すことなく、$\boldsymbol{A}\rightarrow \boldsymbol{A'}, \phi\rightarrow\phi'$の変換ができます。これをゲージ変換と言います。この変換によって残り2つの式
-\nabla^2\phi - \nabla\cdot\frac{\partial\boldsymbol{A}}{\partial t} = \frac{\rho}{\varepsilon}\\
c^2(\nabla(\nabla\cdot\boldsymbol{A})-\nabla^2\boldsymbol{A}) = \frac{\boldsymbol{J}}{\varepsilon}+\frac{\partial}{\partial t}\left(-\nabla\phi - \frac{\partial\boldsymbol{A}}{\partial t}\right)
も式の形を変えずに成り立ってしまいます。結局、ある特定の電場磁場における電磁ポテンシャルは$\chi$によって無限に存在することになったわけです。
ゲージ変換を逆手にとって式を簡単にする
電場と磁場に対応する電磁ポテンシャルがゲージ変換のもとで無限に存在するなら、それを逆手にとって式を簡単にできます。
もう一度この2式をみるとかなり計算が大変な形をしています
-\nabla^2\phi - \nabla\cdot\frac{\partial\boldsymbol{A}}{\partial t} = \frac{\rho}{\varepsilon}\\
c^2(\nabla(\nabla\cdot\boldsymbol{A})-\nabla^2\boldsymbol{A}) = \frac{\boldsymbol{J}}{\varepsilon}+\frac{\partial}{\partial t}\left(-\nabla\phi - \frac{\partial\boldsymbol{A}}{\partial t}\right)
この2つ目の式をこうしてみます
\left(\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)\boldsymbol{A}-\nabla\left(\nabla\cdot\boldsymbol{A} + \frac{1}{c^2}\frac{\partial\phi}{\partial t}\right) = -\mu\boldsymbol{J}
この式、第2項消えて欲しくないですか?$\phi$と$\boldsymbol{A}$が混在してるとか複雑すぎでしょ。
もし
\nabla\cdot\boldsymbol{A} + \frac{1}{c^2}\frac{\partial\phi}{\partial t} = 0
だったとき、先のもう片方の式も
-\nabla^2\phi - \nabla\cdot\frac{\partial\boldsymbol{A}}{\partial t} = \frac{\rho}{\varepsilon}\\
\Rightarrow -\nabla^2\phi+\frac{1}{c^2}\frac{\partial^2\phi}{\partial t^2} = \frac{\rho}{\varepsilon}
になって$\phi$と$\boldsymbol{A}$を分離できるんですけど。。。
ローレンツ条件
ここまでの内容をまとめると
\nabla\cdot\boldsymbol{A} + \frac{1}{c^2}\frac{\partial\phi}{\partial t} = 0
これが成り立てばマクスウェル方程式を
\left(\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)\boldsymbol{A} = -\mu\boldsymbol{J}\\
\left(\nabla^2\phi-\frac{1}{c^2}\frac{\partial^2\phi}{\partial t^2}\right) = -\frac{\rho}{\varepsilon}
にすることができます。この条件をローレンツ条件と言います。
弱点をつけ
我々は電磁ポテンシャルの弱点をもう知っています。ゲージ変換です。ゲージ変換によってローレンツ変換を正しいものとすればいいのです。
ゲージ変換の内容は「$\boldsymbol{A},\phi$は適当な$\chi$を介して任意の$\boldsymbol{A'},\phi'$に変換できる」です。その手順は「$\boldsymbol{A'} = \boldsymbol{A} + \nabla\chi$と置き換え、$\phi' = \phi - \partial\chi/\partial t$とする」でした。これをそのままローレンツ条件に入れてみると、
\nabla\cdot(\boldsymbol{A}+\nabla\chi) + \frac{1}{c^2}\frac{\partial}{\partial t}\left(\phi - \frac{\partial\chi}{\partial t}\right) = 0\\
\nabla\cdot\boldsymbol{A} + \frac{1}{c^2}\frac{\partial\phi}{\partial t} + \nabla^2\chi - \frac{1}{c^2}\frac{\partial^2\chi}{\partial t^2} = 0\\
\left(\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)\chi = -\left(\nabla\cdot\boldsymbol{A} + \frac{1}{c^2}\frac{\partial\phi}{\partial t}\right)
となって、確かに$\chi$が存在することがわかりました。具体的な値はどうでもよく、存在しさえすれば電磁ポテンシャルの式は
\left(\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)\boldsymbol{A} = -\mu\boldsymbol{J}\\
\left(\nabla^2\phi-\frac{1}{c^2}\frac{\partial^2\phi}{\partial t^2}\right) = -\frac{\rho}{\varepsilon}\\
\nabla\cdot\boldsymbol{A} + \frac{1}{c^2}\frac{\partial\phi}{\partial t} = 0
にまとめられます。電場と磁場の発散系と回転系の4つの式でしかも電場と磁場が1つの式で混在していたものが、ローレンツ条件を介してベクトルポテンシャル、スカラーポテンシャルの独立した式になってしまいました。
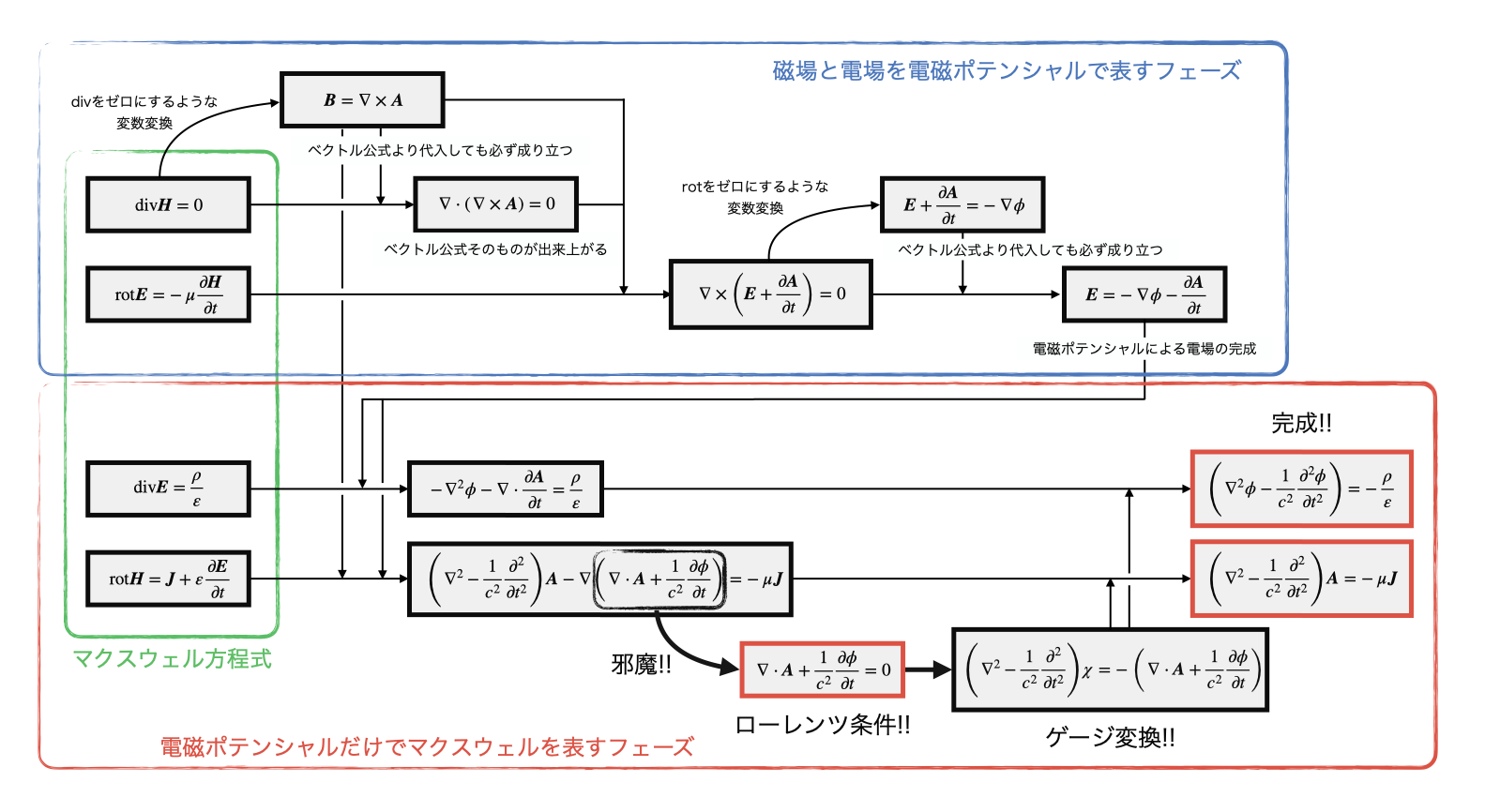
図で流れをおさらい
ここまでくると、「なんで式3つになったの??」と混乱すると思いますので、図で導出過程を描いてみました。
次回の予定
次回以降は電磁ポテンシャルを使っていろんな定理や現象を表して行けたらいいなと思います。