はじめに
先日発行されました情報処理学会誌1月号で「機械学習応用システムのテスト・検証」という記事を書きましたが、スペースの制約などがあり、メタモルフィックテスティングについて十分な量を書けていません。また執筆後にメタモルフィックテスティングの提唱者であるTsong Yueh Chen先生の講演を聞いたり、他の文献を読んだりした中で、もう少し書き足したい部分もあり、そのようなところを中心にメタモルフィックテスティングについて解説します。
解決する問題:期待値が分からないテストの成否をどう決める?
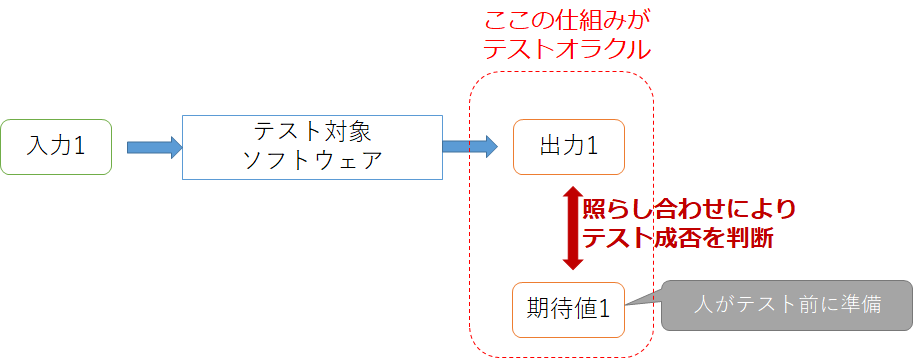
一般的にソフトウェアのテストの成功・失敗を決める際、テストケースごとに期待値(期待結果、確認項目などとも言われたりします)があり、実際にテストケースを実行したときの出力と比べることをします。このときの「ソフトウェアに対するテストが成功か失敗かを判定するメカニズム」のことをテストオラクルと呼びます。
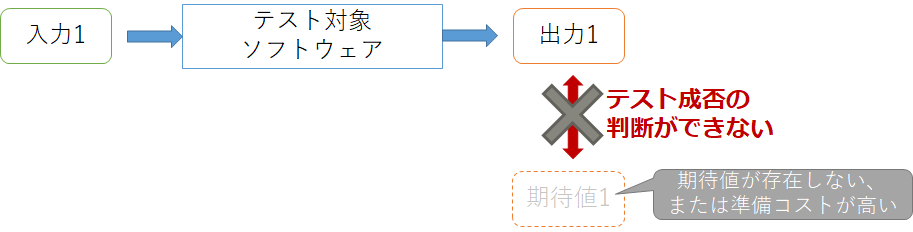
しかし必ずしもどんなソフトウェアでもテストオラクルを用意できるわけではありません。ソフトウェアによっては期待値がわからなかったり、期待値を準備するコストが高い場合があるからです。例えば数値計算のテストなら、要求される精度を満たす具体的な値を人間が計算して準備するのは困難です。またコンパイラのテストなら、出力されるバイナリファイルから本当にソースファイルで記述されていることが反映されているかを確認するのは同じく困難です。このようなプログラムのことを**テスト不可能プログラム(Non-Testable Program)**と言います。
機械学習システムもテスト不可能プログラムの1つと考えられることが多く、例えば訓練アルゴリズムが正しくモデルを構築できたかは、モデルのパラメータやモデルの精度で判断するのは難しいので、期待値を直接用意する以外の方法でテスト成否の判断をしなくてはなりません。
メタモルフィックテスティングとは
メタモルフィックテスティングはテスト不可能プログラムに対して疑似的にテストオラクルを用意する手法の1つです。「入力に対してある一定の変化を与えたときに、出力の変化が理論上予想できる」という関係(メタモルフィック関係(Metamorphic Relation))を用いて、複数の入力を用意しそれらの出力間の関係を比較することでテストの成否を決めます。よく使われる例としては、$sin(x)$を計算するプログラムに対するテストを考えるときに2つの入力$x$, $x+2\pi$は同じ出力を持つというメタモルフィック関係を用いて、$sin(x)=sin(x+2\pi)$を確認することでテスト成否を決められます。
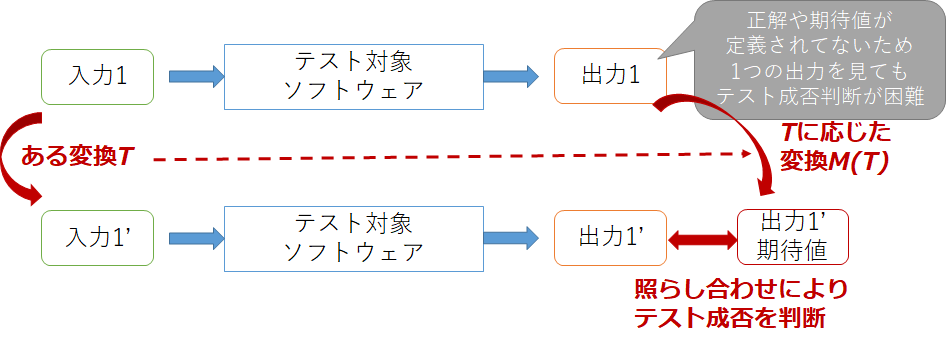
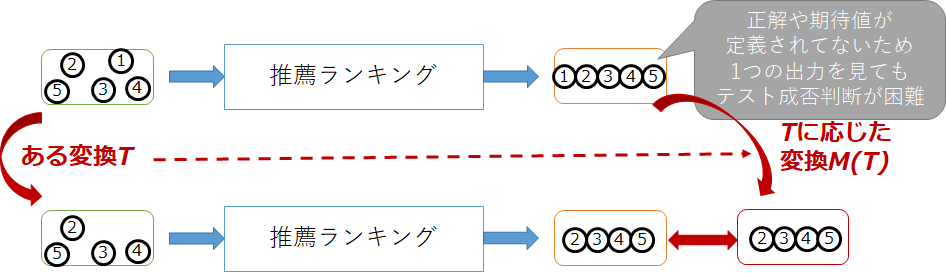
他の例として購買データから商品の推薦ランキングを出力するシステムを考えます。1位の商品を除いた購買データでは、元が2位3位だった商品が繰り上がって1位2位になるという性質をメタモルフィック関係とし、その出力と、元の購買データを用いた出力から1位を除いたものを比べることでテスト成否を決めることができます。
機械学習システムへのメタモルフィックテスティング適用
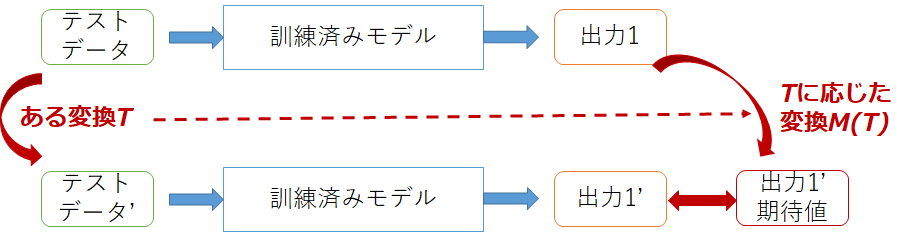
教師あり機械学習を用いたシステムへメタモルフィックテスティングを適用する場合、大きく分けて2つの適用パターンがあります。1つが訓練済みモデルに対してテストするパターンで、テストデータに対して変換を行い、その出力と通常のテストデータとの出力を比較します。
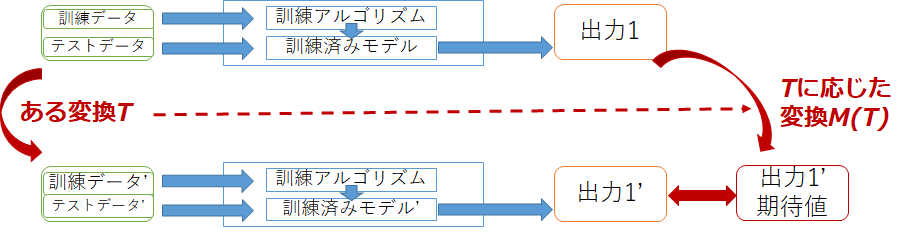
もう1つが訓練アルゴリズムに対するテストで、テストデータだけではなく訓練データも含め入力として見なし、両方に対して変換を行います。そしてそれぞれの訓練データを用いて訓練アルゴリズムを実行し訓練済みモデルを生成し、それぞれの訓練済みモデルに対してテストデータを実行したときの出力を比較します。
機械学習システムへのメタモルフィックテスティング適用した事例のうちのいくつかを以下に示します。
| アルゴリズム・アプリケーション | テスト対象 | メタモルフィック関係 | 参考文献 |
|---|---|---|---|
| 深層学習による自動運転 | 訓練済みモデル | 入力画像に雨や霧に相当するノイズを追加したときのハンドル角の予測値と元の予測値との差の二乗が訓練データにおける平均二乗誤差以下であること | [1] |
| SVM,深層学習による画像分類 | 訓練アルゴリズム/訓練済みモデル | RGBチャネルの入れ替えたデータや転置した畳み込み演算(行列)で訓練したモデルでも分類結果が変わらないこと/正規化した画像や特徴量を定数倍した画像でも分類結果が変わらないこと | [2] |
| クラスタリング | クラスタリングアルゴリズム | データの中心点への移動,中心点付近へのデータ追加などでクラスタリング結果が変わらないこと | [3] |
| 時系列データ分析 | 訓練済みモデル | 幾何学変換した出力と,幾何学変換した入力に対する出力が等しいこと | [4] |
| k近傍法,単純ベイズ分類器 | 訓練アルゴリズム | アフィン変換されたデータや,複製が加わったデータセットなどで訓練したモデルでも分類結果が変わらないこと | [5] |
[1] Tian, Yuchi, et al. "Deeptest: Automated testing of deep-neural-network-driven autonomous cars." Proceedings of the 40th International Conference on Software Engineering. ACM, 2018. (https://arxiv.org/abs/1708.08559)
[2] Dwarakanath, Anurag, et al. "Identifying implementation bugs in machine learning based image classifiers using metamorphic testing." Proceedings of the 27th ACM SIGSOFT International Symposium on Software Testing and Analysis. ACM, 2018. (https://arxiv.org/abs/1808.05353)
[3] Xie, Xiaoyuan, et al. "METTLE: A Metamorphic Testing Approach To Validating Unsupervised Machine Learning Methods." arXiv preprint arXiv:1807.10453 (2018). (https://arxiv.org/abs/1807.10453)
[4] Jarman, Darryl C., Zhi Quan Zhou, and Tsong Yueh Chen. "Metamorphic testing for Adobe data analytics software." Proceedings of the 2nd International Workshop on Metamorphic Testing. IEEE Press, 2017. (https://ro.uow.edu.au/cgi/viewcontent.cgi?article=1418&context=eispapers1)
[5] Xie, Xiaoyuan, et al. "Testing and validating machine learning classifiers by metamorphic testing." Journal of Systems and Software 84.4 (2011): 544-558. (https://mice.cs.columbia.edu/getTechreport.php?techreportID=1415&format=pdf&)
類似の概念
メタモルフィックテスティングにはいくつか類似の概念があるので、その違いについて見て行きましょう。
類似の概念1:Nバージョンプログラミング
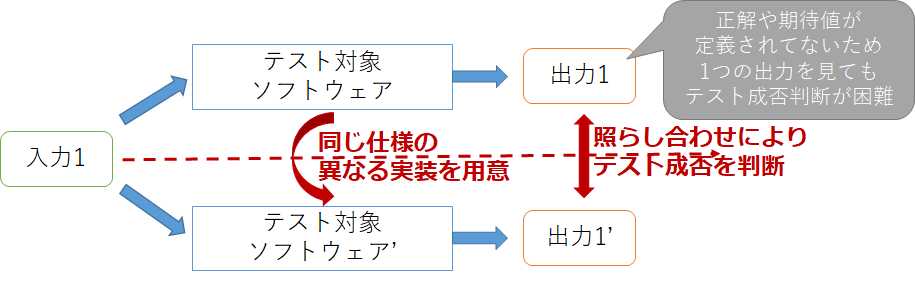
Nバージョンプログラミングはメタモルフィックテスティングと同じくテスト不可能プログラムに対して疑似的にテストオラクルを用意する手法になります。メタモルフィックテスティングは2つの入力(元の入力とそれを変換した入力)を用意するのに対し、Nバージョンプログラミングは1つの入力に対し複数の実装を用意し、それぞれの実装の出力を比べることでテストの成否を決めます。これらの違いはデータ多様性、デザイン多様性という考え方で区別することもできます。
Nバージョンプログラミングの例としては、Cコンパイラのテストで対象コンパイラの出力とgccやclangといった実装の出力(アセンブリ)と比較する方法があります。実装が3つ以上あれば多数決で正しさを決めることもできますが、実装が2つの場合はどちらの実装が誤っているかを判断するのは人の判断によることになります。
類似の概念2:プロパティベーステスト
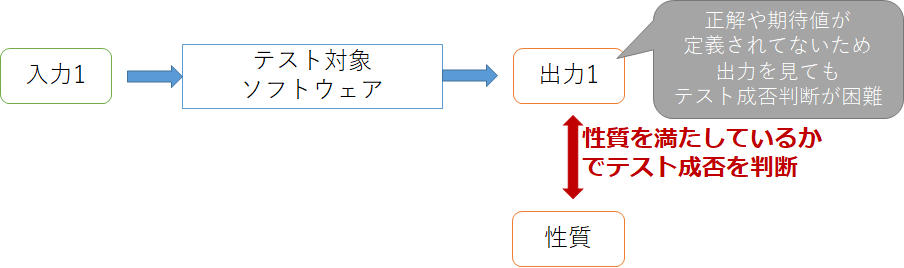
プロパティベーステストは期待値を具体的な値とせず、ある入力の範囲で満たす性質を記述し、それをチェックすることでテストオラクルとします。例えば$sin(x)$の実装の場合、満たすべき性質は任意の$x$で$-1\le sin(x)\le 1$となります。メタモルフィックテスティングでも2つの入出力間の性質(メタモルフィック関係)をチェックしますが、プロパティベーステストでは基本的に1つの入力でもテスト成否を判断できます。ただ、2入出力間の性質をチェックするという意味ではメタモルフィックテスティングはプロパティベーステストの一種だと考えることもできるかもしれません。
プロパティベーステストはテスト入力をランダムに生成する手法であるランダムテストと一緒に使われることが多く、実装としてはHaskellのQuickCheckが有名です。
類似の概念3:Data Augmentation
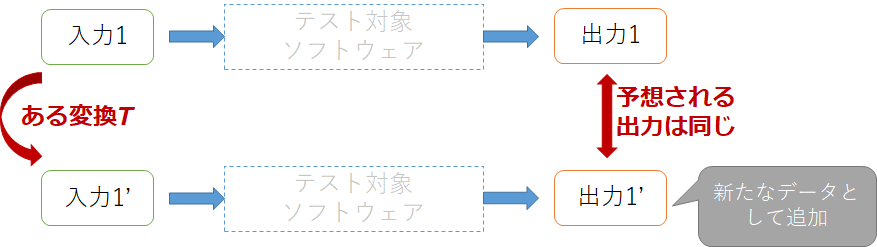
Data augmentationは機械学習における手法の1つで、既存のデータから新たなデータを生成しデータの水増しをする方法です。具体的には出力の変化が理論上予測できるように既存の入力を変換し、それらを新たなデータとして加えます。基本的には期待する出力もセットで生成し訓練データを水増しすることで精度の改善を目的とします。一方、メタモルフィックテスティングでも同じように新たな入力を生成しますが、テストを目的にするためテストデータを対象にする点と、出力を予め用意する必要がない点が異なります。
よくある疑問・議論
メタモルフィックテスティングを使う際にしばしば議論となる点について(私見も交えて)紹介します。
メタモルフィック関係はどうやって特定するのか?
メタモルフィックテスティングにおいてメタモルフィック関係が非常に重要な役割を果たしますが、ではメタモルフィック関係はどうやって導き出されるものなのでしょうか。これまで論文などで多くのメタモルフィック関係が提案されてきており、その特定方法について多くの報告で難しくないとされていますが、どれもアドホックで恣意的なものに見えます。メタモルフィック関係特定のための単純なアプローチとしては、まず1つの入力を選択し、出力を予想できるような変化をその入力に加えてみて、その関係が一般化できるようであれば、それがメタモルフィック関係になります。他にもシステマティックにメタモルフィック関係を特定する手法が提案されていますが、いずれにしても対象ソフトウェアをよく知る開発者の知識が必要となるため、そのあたりはメタモルフィックテスティング適用の1つのハードルになると考えます。
メタモルフィックテストで十分なのか?
メタモルフィックテスティングはテスト不可能プログラムに対してテストを行う効果的な方法ではありますが、ではメタモルフィックテスティングだけでテストは十分なのでしょうか。基本的にメタモルフィックテスティングは2つの入出力に存在する性質についてチェックをするもので、仕様のうちの一部しかテストしていることにならず、すべてを包括的にテストできるわけではありません。1つの観点だけではなく多角的にテストすることが重要であって、メタモルフィックテスティングはそのための1手法だと考えるとよいと思います。ただ、機械学習システムへの適用事例で紹介した[2]の論文ではメタモルフィックテスティングにより71%のバグを検出できたという報告もあるので、うまく使うことで強力な手法になると考えられます。