はじめに
@toku_sanと申します。初投稿なので、文章の拙さはご容赦ください。
前提知識:正規分布って何?
正規分布(ガウス分布)とは、
横軸に確率変数$X$、縦軸に確率密度を取った、

↑こんな感じのグラフ(今回は平均$=0$、分散$=1$です)。
数式だと、$X$に関する確率密度関数$F(X)$として
F(X)=\frac{1}{\sqrt{2\pi \sigma_x^2}}\exp{\left\{-\frac{(X-\mu_x)^2}{2\sigma_x^2}\right\}}
になります。
※平均は$\mu_x$、分散は$\sigma_x^2$。
前提知識はここまで。
もっと詳しく知りたい人は、ググって下さい。
確率変数の絶対値を取った時、平均と分散がどうなるか?
試しに、先のグラフにおいて$X$の絶対値を取ったグラフを描画して、
絶対値を取る前と比較してみる
(スペースの都合上、図の縦の縮尺が変わってます)。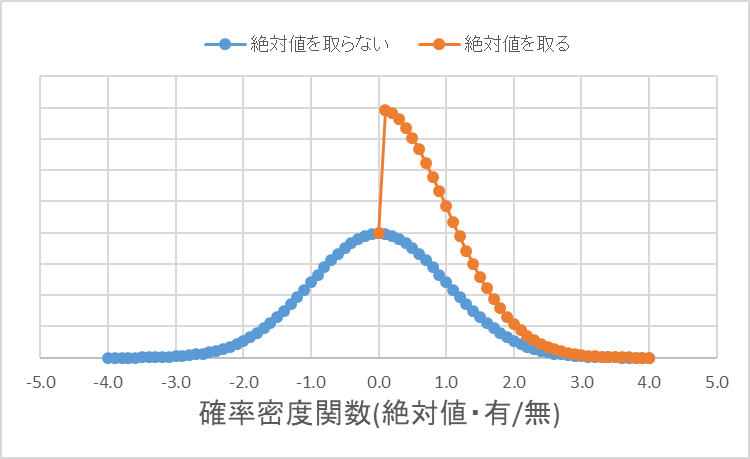
分布のイメージはつかめたが、平均と分散に関しては、分からない。
そこで、まず$X$の絶対値を取った平均値$\mu_{|x|}$を定義通り表す。
\mu_{|x|}=\int_{-\infty}^{\infty}|X|F(X)dX=\int_{-\infty}^{\infty}|X|\frac{1}{\sqrt{2\pi\sigma_x^2}}{\rm exp}\left(-\frac{\left(X-\mu_x\right)^2}{2\sigma_x^2}\right)dX
そして、ゴリゴリ計算すると...
\mu_{|x|}=\sqrt{\frac{2\sigma_x^2}{\pi}}{\rm
exp}\left(-\frac{\mu_x^2}{2\sigma_x^2}\right)+\mu_x\left(1-{\rm
erfc}\left(\sqrt{\frac{\mu_x^2}{2\sigma_x^2}}\right)\right)
となる。(ここまで来たらC言語でもラクラク計算できる)
途中計算は長いので"ここでは"省略する。
ちなみに分散$\sigma_{|x|}^2$は、定義通り
\sigma_{|x|}^2=\int_{-\infty}^{\infty}(|X|-\mu_{|x|})^2F(X)dX
をこれまたゴリゴリ計算して、
\sigma_{|x|}^2=\sigma_x^2+\mu_x^2-\mu_{|x|}^2
となる。
研究や学会でどうしても各絶対値を求める途中式が知りたい方は、
絶対値を取った確率密度関数の平均と分散(式変形編)を参照して下さい。
結論
絶対値を取った確率密度関数の平均と分散は定義に戻って、
"ゴリゴリ"計算すれば導出できる。