Quaternionの数学的理解メモ その1
Quaternionの数学的理解メモ その2
クォータニオンによる回転
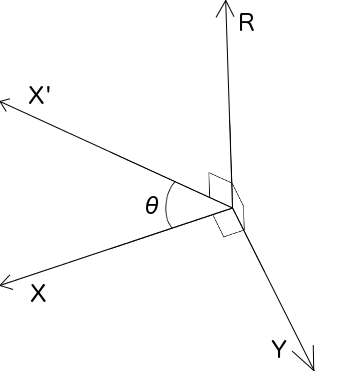
回転軸とベクトルが直交している場合
xからx'に回転する事を考える。
ベクトルyを以下のように定義する。
Y≡XR
ベクトルxと回転軸rは直交している為、
\begin{array}{ccl} Y & = & XR \\ & = & -[[x\cdot r,\quad \sigma _{ 1 }(x\times r)_{ 1 }+\sigma _{ 2 }(x\times r)_{ 2 }+\sigma _{ 3 }(x\times r)_{ 3 }]] \\ & = & -[[0, \quad \sigma _{ 1 }(x\times r)_{ 1 }+\sigma _{ 2 }(x\times r)_{ 2 }+\sigma _{ 3 }(x\times r)_{ 3 }]] \end{array}
となる。この時ベクトルy,x,x'は同一平面上に存在する。
よって、
\begin{array}{ccl} X' & = & Xcos\theta +Ysin\theta \\ & = & X(Ecos\theta +Rsin\theta ) \\ & = & X[[cos\theta ,\quad \sigma _{ 1 }r_{ 1 }sin\theta +\sigma _{ 2 }r_{ 2 }sin\theta +\sigma _{ 3 }r_{ 3 }sin\theta ]] \end{array}
上の式が前回の最後の式と等しい事はXがユニタリ行列かつ逆エルミート行列であることを用いれば分かる。
任意軸の場合
x=x_{\bot}+x_{\parallel}
ベクトルxを回転軸rに直交するものと平行なものに分離して考えると、
\begin{array}{ccl} X' & = & X_{ \bot }cos\theta +Ysin\theta +X_{ \parallel } \\ & = & X_{ \bot }V(\theta )+X_{ \parallel } \\ & = & X_{ \bot }V(\theta /2)V(\theta /2)+X_{ \parallel } \\ & = & \left( X_{ \bot }V(\theta /2) \right) cos\frac { \theta }{ 2 } +\left( X_{ \bot }V(\theta /2) \right) Rsin\frac { \theta }{ 2 } +X_{ \parallel } \\ & = & \left( X_{ \bot }V(\theta /2) \right) cos\frac { \theta }{ 2 } -R\left( X_{ \bot }V(\theta /2) \right) sin\frac { \theta }{ 2 } +X_{ \parallel } \\ & = & \left( cos\frac { \theta }{ 2 } -Rsin\frac { \theta }{ 2 } \right) \left( X_{ \bot }V(\theta /2) \right) +X_{ \parallel } \\ & = & V^{ * }(\theta /2)X_{ \bot }V(\theta /2)+X_{ \parallel } \\ & = & V^{ * }(\theta /2)X_{ \bot }V(\theta /2)+V(\theta /2)V^{ * }(\theta /2)X_{ \parallel } \\ & = & V^{ * }(\theta /2)X_{ \bot }V(\theta /2)+V^{ * }(\theta /2)X_{ \parallel }V(\theta /2) \\ & = & V^{ * }(\theta /2)XV(\theta /2) \end{array}
途中以下の外積の性質を用いている。
x \times y= -y \times x
ちなみにこの変換はユニタリ変換の一つである
回転の合成
行列の結合性からすぐ可能であることが分かる。