どうも、趣味で関数型言語をやっている者です。
これは 言語実装 Advent Calendar の2日目の記事です。
導入
みなさま ラムダ計算 をご存知でしょうか。
ラムダ計算はある種の関数型プログラミング言語の体系で、変数と関数、そして関数適用というミニマルな構成要素だけでチューリング完全な表現力を持っています。
今回はラムダ計算の中でも特に単純な 型無しラムダ計算 に着想を得て、型無しラムダ計算のステップ評価器を作った(作っている)話について書きます。
既存のモデルへの不満
型無しラムダ計算を具体的な実装に落としたものとしては、有名なところで Unlambda や Lazy_K などがあります。
どちらも SKI コンビネーター理論 に基づいており、 s, k, i という たった3つの組み込み関数でプログラムを記述することが可能 1 です。
かく言う私も Unlambda から型無しラムダ計算に入門したクチです。しかし、従来の言語には長らく不満がありました。それは関数の計算過程が印字不可で、計算の過程が非常に見えづらいことです。
早い話、 Unlambda や Lazy_K は print デバッグできないのがツラい という事なのですが。私の見立てではこの「print デバッグで試行錯誤できない感」が ラムダ計算の世界から入門者を遠ざけている要因になっている ように思います。
ラムダ計算の計算過程を見える化する
そこで、『無いものは作ればいい精神』です。型無しラムダ計算学習用 ステップ評価器 Mogul 2 を作りました。
実際の動作を見てもらう方がイメージしやすいと思うので GIF を、
ラムダ式をステップ評価する様が見て取れると思います。
今のところ
- 論理演算 (
NOT,AND,OR,XOR) - 整数(チャーチ数)の操作 (後者関数
SUCC, 前者関数PRED) - 整数(チャーチ数)の演算 (和
ADD, 差SUB, 積MUL) - 整数(チャーチ数)の同士の比較 (ゼロ比較
ISZERO, 等値比較EQ, 不等比較GT,LT) - 連結リスト操作 (
CONS,CAR,CDR) - 無名再帰 (
Yコンビネータ) - 自作関数の定義
などが出来ます。
セットアップ
実際に触ってみたい方のためにセットアップして実行するまでの方法を軽く解説します。
セットアップには Git と Stack (Haskell のパッケージマネージャ) が必要です。
Git, Stack がセットアップ済みであれば、あとはコマンドラインで
$ git clone https://github.com/todays-mitsui/Mogul.git
$ cd Mogul
$ stack setup
$ stack build
$
$ #実行
$ stack exec mogul
とすれば GitHub からソースを落としてきて、ビルドして、実行するところまでやってくれます。
アンインストールは Mogul ディレクトリを丸ごと削除するだけで OK です。
シンタックス
Mogul の記法について簡単に解説してみます。
関数適用 (関数実行)
まず、 i という組み込みの関数があります。 Identity の略で、引数をそのまま返す関数です。
> i
i
0 steps, done.
このように、残念ながら i 単体を評価しても何も起きません。
では、関数 i に引数 x を与えて実行してみましょう。バッククォート ` の後に i と x を並べることで関数を実行できます。
> `ix
`ix
⇒ x
1 steps, done.
はい、実行結果は x です。
このように関数に引数を与えて実行することを 関数適用 と云います。この場合 i に x を適用しました。
他にも組み込み関数を使ってみましょう。定数関数 k は2つの引数を取り、2つめの引数を捨てて1つめの引数をそのまま返します。
k は Constant (Konstant) の略ですね、たぶん。
``kxy
⇒ x
1 steps, done.
「2つの引数を取る」と書きましたが、これは正確な表現ではありません。厳密には Mogul の世界には多変数関数が存在せず、1引数関数しか扱えないからです。
kxy を厳密に解釈すると、 `k` に `x` を適用した結果に `y` を適用していると読めます。とはいえ、まぁ、関数を実行するためには引数の個数と同じだけ ` `` を打たなければいけないと覚えておいてください。
もう一つ欠かせない関数 s を使ってみましょう。
s は Substitution の略で、3引数 x, y, z を与えると ``xz`yz を返します。
> ```sxyz
```sxyz
⇒ ``xz`yz
1 steps, done.
関数合成 や 引数の入れ替え を実現するために重要な関数です。
関数抽象と関数定義
ラムダ計算に欠かせないのが 関数抽象 です。
モダンなプログラミング言語に親しんだ方であれば 無名関数 または クロージャー (closure) の事だと云えば伝わりやすいでしょうか。
引数 x に対して `xx を返す関数抽象を以下のように書きます。
^x.`x.x
^x. の部分が仮引数、 `x.x の部分が関数本体です。
関数抽象に引数を与えて評価することができます。 a を適用してみましょう。
> ` ^x.`xx a
`^x.`xxa
⇒ `aa
1 steps, done.
いいですね。
関数定義
関数抽象は 別の変数に代入する こともできます。
> FOO=^x.`xx
> `FOOa
`FOOa
⇒ `^x.`xxa
⇒ `aa
2 steps, done.
このようにして自作関数 FOO を定義することができました。これが 関数定義 です。
多変数関数
多変数関数は関数抽象をネストさせることで実現します。
> ^x.^y.`yx
^x.^y.`yx
0 steps, done.
> `` ^x.^y.`yx a b
``^x.^y.`yxab
⇒ `^y.`yab
⇒ `ba
2 steps, done.
上手く動いていますね。
このように1引数の関数抽象をネストさせて多変数関数を表現する方法を カリー化 と云います。
関数の定義を参照する
ここまでに見てきたように、 Mogul では関数適用を変数に代入することで自作の関数を定義することが出来ます。
逆に定義済みの関数の定義を参照するには :info コマンド を使います。
> :info s
s=^x.^y.^z.``xz`yz
組み込み関数 s が ^x.^y.^z.``xz`yz のシノニムであることが分かります。
:info コマンドの代わりに短縮記法 ? を使う事もできます。
> ? s
s=^x.^y.^z.``xz`yz
Mogul には他にも多くの組み込み関数が定義されています。 :context コマンド を使うことで全ての定義済み関数を見ることができます。
> :context
0=^f.^x.x
1=^f.^x.`fx
...
SUB=^m.^n.``n PREDm
SUCC=^n.^f.^x.`f``nfx
TRUE=^x.^y.x
XOR=^x.^y.``x`NOTyy
Y=^f.`^x.`f`xx^x.`f`xx
i=^x.x
k=^x.^y.x
s=^x.^y.^z.``xz`yz
デフォルトで定義済みの関数は default.mgl をご覧ください。
最終の評価だけ見る
ラムダ式の評価はときに多くのステップを要します。たとえば 5 == 2 + 3 を確かめるためのラムダ式 ``EQ 5 ``ADD 2 3 は173ステップの後に TRUE に評価されます。が、ときには最終結果だけ見たいときもあるでしょう。
そういうときには :last コマンド を使います。短縮記法は ! です。
> :last ``EQ 5 ``ADD 2 3
``EQ 5``ADD 2 3
⇒ ...
⇒ TRUE
173 steps, done.
> ! ``EQ 12 ``ADD 7 6
``EQ 12``ADD 7 6
⇒ ...
⇒ FALSE
303 steps, done.
終了する
インタプリタの終了は :quit コマンド または Ctrl+C です。
Mogul で計算っぽいことをやってみる
遊んでみましょう。
論理演算
論理演算のために必要な一通りの関数が用意されています。
TRUE, FALSE, NOT, AND, OR, XOR などです。
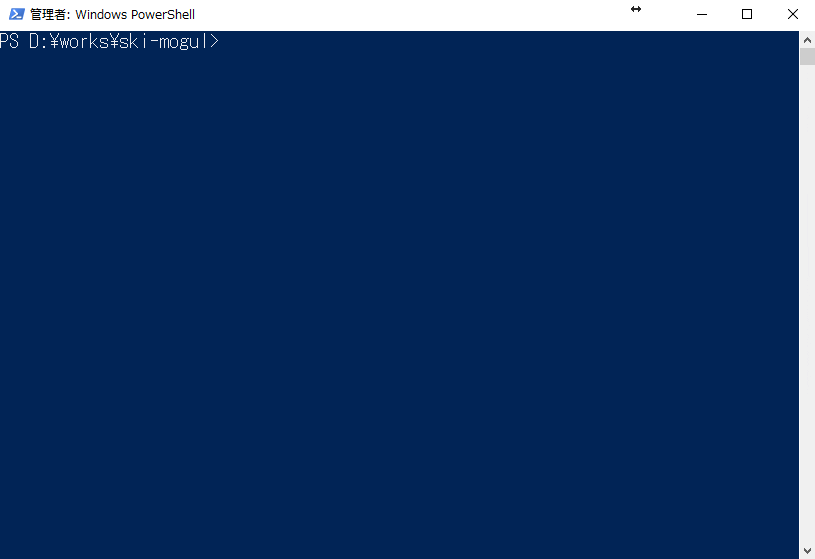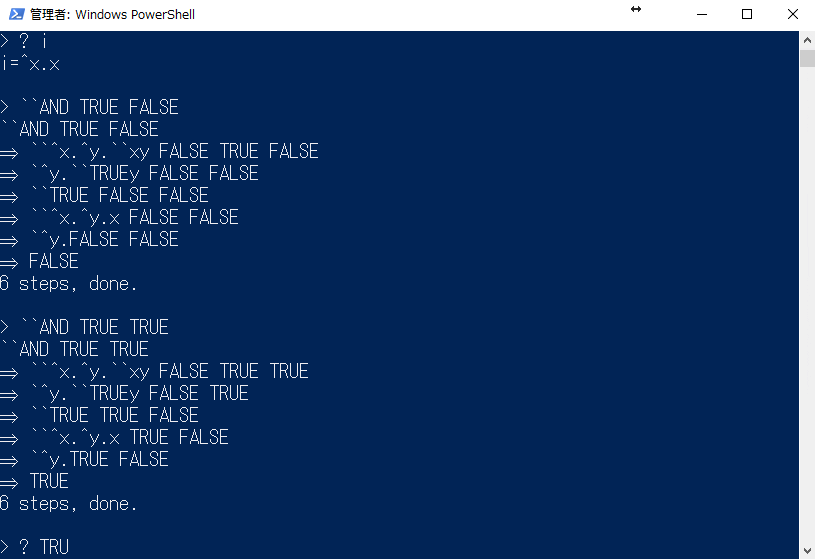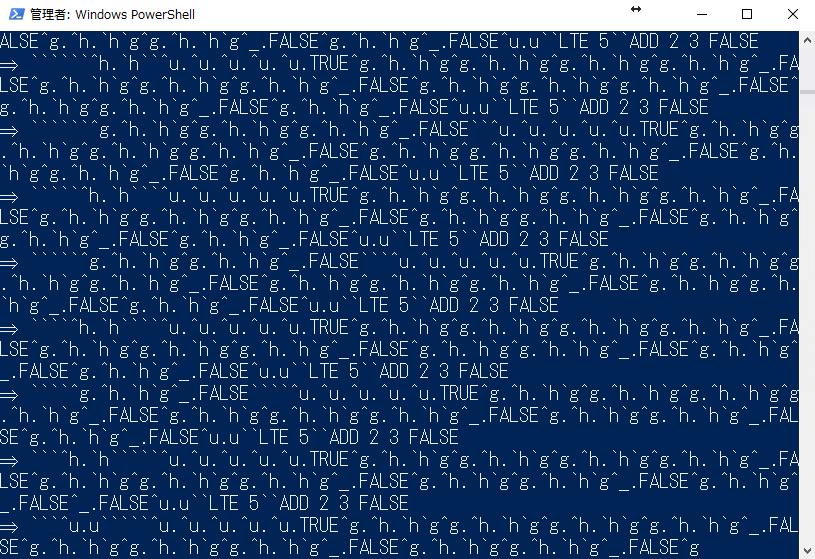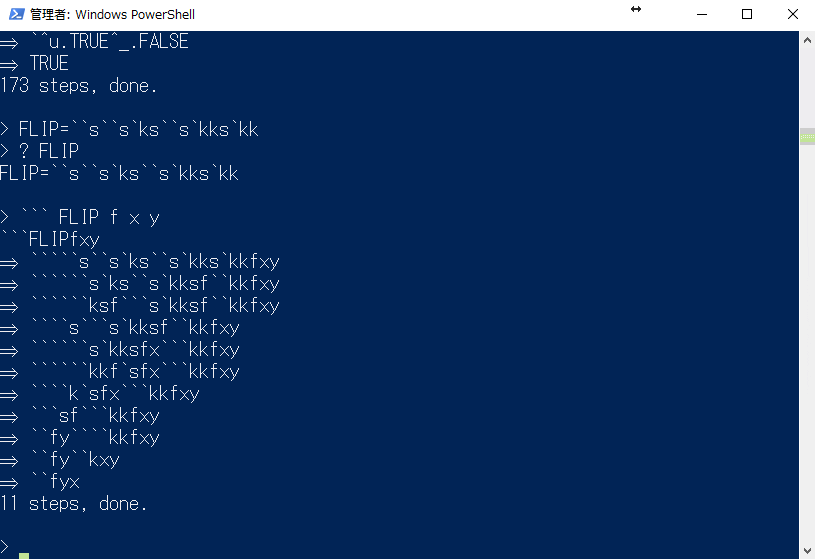
> ! ``AND TRUE FALSE
``AND TRUE FALSE
⇒ ...
⇒ FALSE
6 steps, done.
> ! ``AND TRUE `NOT FALSE
``AND TRUE`NOT FALSE
⇒ ...
⇒ TRUE
11 steps, done.
> ! ``AND ``OR FALSE TRUE `NOT FALSE
``AND``OR FALSE TRUE`NOT FALSE
⇒ ...
⇒ TRUE
17 steps, done.
IF を使うと if式 っぽいものを書くこともできます。
> ```IF FALSE x y
```IF FALSExy
⇒ ```^BOOL.^THEN.^ELSE.``BOOL THEN ELSE FALSExy
⇒ ``^THEN.^ELSE.``FALSE THEN ELSExy
⇒ `^ELSE.``FALSEx ELSEy
⇒ ``FALSExy
⇒ ``^x.^y.yxy
⇒ `^y.yy
⇒ y
7 steps, done.
整数演算
0 ~ 128 までの整数 3 は定義済みです。
和 ADD, 差 SUB , 積 MUL を計算することもできます。
> ``ADD 2 3
``ADD 2 3
⇒ ``^m.^n.^f.^x.``mf``nfx 2 3
⇒ `^n.^f.^x.``2f``nfx 3
⇒ ^f.^x.``2f``3fx
3 steps, done.
この評価結果はラムダ計算的に正しいのですが、最終結果を見ても釈然としないかも知れませんね。
``ADD 2 3 の結果に対してさらに a と b を適用してみましょう。
> `` ^f.^x.``2f``3fx a b
``^f.^x.``2f``3fxab
⇒ `^x.``2a``3axb
⇒ ``2a``3ab
⇒ ``^f.^x.`f`fxa``3ab
⇒ `^x.`a`ax``3ab
⇒ `a`a``3ab
⇒ `a`a``^f.^x.`f`f`fxab
⇒ `a`a`^x.`a`a`axb
⇒ `a`a`a`a`ab
8 steps, done.
b に対して a が 5 回 実行された形になりました。これがラムダ計算の世界でいうところの 5 の表現です。
もう少し詳しく知りたい方は チャーチ数 について調べてみてください。
実装
Mogul は Haskell で実装されています。
が、実は Mogul のコンセプトである「ラムダ式のステップ評価」と Haskell の醍醐味である「遅延評価 & 関数再帰呼び出し」の相性が悪くて苦労しました。
じゃあなんで Haskell で実装したんだよという話ですが、私が Haskell くらいでしかまともに Parser を書けないので、というのが理由です。
実装についてはいろいろと試行錯誤中なので強い Haskeller さんにアドバイスいただけると喜びます。
全てのソースコード は GitHub に置いています。
今後の展望
最初にも書いたように、私が Mogul を書き始めた動機は ラムダ計算の入門者のハードルを下げること です。だいたい6~10歳くらいの小学生がシンプルに自然にラムダ計算を学び始められる世界を夢見ています。
今は CUI しかインターフェースがありませんが、小学生に向かって「とりあえずコマンドラインを起動して」というのも無理があると思っています。
といわけで Mogul の目下のアップデート予定は、 Web API化 そして Webアプリ化 です。誰もが気軽にブラウザを立ち上げるだけでラムダ計算に親しめる世界を目指して。
2019年7月5日 追記、
できました。まだまだバグだらけですが。
私からは以上です。4