バックエンド、フロントエンドをいろいろカジってきましたが、機械学習は未挑戦でした。今般、初挑戦しましたので記念に記録しておきます。python、numpy、tf.kerasを使っています。
マイスペック
- このQiita参照。
- cやgoによる通信系〜バックエンド開発、flutter/dartによるフロントエンド開発が可能。
- pythonも結構触っている。
- 機械学習はGUIのツールでちょっと触ってみたことはある。
- pythonでの機械学習は初挑戦。numpyも使ったことが無かったレベル。
機械学習の理論をまとめて勉強するために「[ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装](https://www.amazon.co.jp/
dp/4873117585/)」を読みました。とても良い本でした。
開発環境はPyCharm Community 2019.3です。Anacondaとかは使わずにPyCharmに必要なライブラリを読み込ませて使っています。
1. 機械学習の課題設定
以下の正解ロジックを、機械学習することを目指します。
- 教師ありの2値分類問題とします。
- 入力する特徴量を2つの乱数値(0以上1未満)として、2つの大小比較によって0か1を正解ラベルとします。
- 正解ラベルには稀にノイズを混入させます。(最初はノイズを無しにします)
2. コード
2値分類問題の典型的コードを、いくつかのWeb記事を見ながら作ってみました。結構、コンパクトに直感的に記述できるものだと思いました。Kerasすごい。
# !/usr/bin/env python3
import tensorflow as tf
import numpy as np
from tensorflow.keras.metrics import binary_accuracy
import matplotlib.pyplot as plt
# データセット準備
ds_features = np.random.rand(10000, 2) # 特徴データ
NOISE_RATE = 0
ds_noise = (np.random.rand(10000) > NOISE_RATE).astype(np.int) * 2 - 1 # noiseなし: 1, あり: -1
ds_labels = (np.sign(ds_features[:, 0] - ds_features[:, 1]) * ds_noise + 1) / 2 # 正解ラベル
# データセットを訓練用と検証用に分割
SPLIT_RATE = 0.8 # 分割比率
training_features, validation_features = np.split(ds_features, [int(len(ds_features) * SPLIT_RATE)])
training_labels, validation_labels = np.split(ds_labels, [int(len(ds_labels) * SPLIT_RATE)])
# モデル準備
INPUT_FEATURES = ds_features.shape[1] # 特徴量の次元
LAYER1_NEURONS = int(INPUT_FEATURES * 1.2 + 1) # 入力次元より少し広げる
LAYER2_NEURONS = LAYER1_NEURONS
LAYER3_NEURONS = LAYER1_NEURONS # 隠れ層は3層
OUTPUT_RESULTS = 1 # 出力は一次元
ACTIVATION = 'tanh'
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(input_shape=(INPUT_FEATURES,), units=LAYER1_NEURONS, activation=ACTIVATION),
tf.keras.layers.Dense(units=LAYER2_NEURONS, activation=ACTIVATION),
tf.keras.layers.Dense(units=LAYER3_NEURONS, activation=ACTIVATION),
tf.keras.layers.Dense(units=OUTPUT_RESULTS, activation='sigmoid'),
])
LOSS = 'binary_crossentropy'
OPTIMIZER = tf.keras.optimizers.Adam # 典型的な最適化手法
LEARNING_RATE = 0.03 # 学習係数のよくある初期値
model.compile(optimizer=OPTIMIZER(lr=LEARNING_RATE), loss=LOSS, metrics=[binary_accuracy])
# 学習
BATCH_SIZE = 30
EPOCHS = 100
result = model.fit(x=training_features, y=training_labels,
validation_data=(validation_features, validation_labels),
batch_size=BATCH_SIZE, epochs=EPOCHS, verbose=1)
# 表示
plt.plot(range(1, EPOCHS+1), result.history['binary_accuracy'], label="training")
plt.plot(range(1, EPOCHS+1), result.history['val_binary_accuracy'], label="validation")
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.ylim(0.5, 1)
plt.legend()
plt.show()
3. 結果
こちかが学習結果です。おおよそ99%くらいの精度にすぐに到達し、過学習もしていないようです。
4. 考察
4.1. ノイズを加えた時の挙動
NOISE_RATE = 0.2 としてみました。ノイズ分だけ精度が低くなりますが、適切な結果に到達しています。
4.2. 無関係なダミーの特徴量を加えた時の挙動
ノイズを戻し、特徴量を5種に増やしてみます。5種のうち2種だけ使って同じロジックで正解ラベルを求めます。すなわち、特徴量の残り3種は、正解とは全く関係無いダミーとなります。
結果はこちらで、多少ブレ幅が大きくなりますが、ダミーに騙されずに学習できているといえます。
4.3. 特徴量の正規化を崩した時の挙動
特徴量を2種に戻しますが、0以上1未満の乱数値を×1000してみました。結果は、学習が一律に収束していかないように見えるほか、最終エポックの近くで精度が悪化しています。
エポックを増やして確認してみました。やはり学習が安定していないようです。
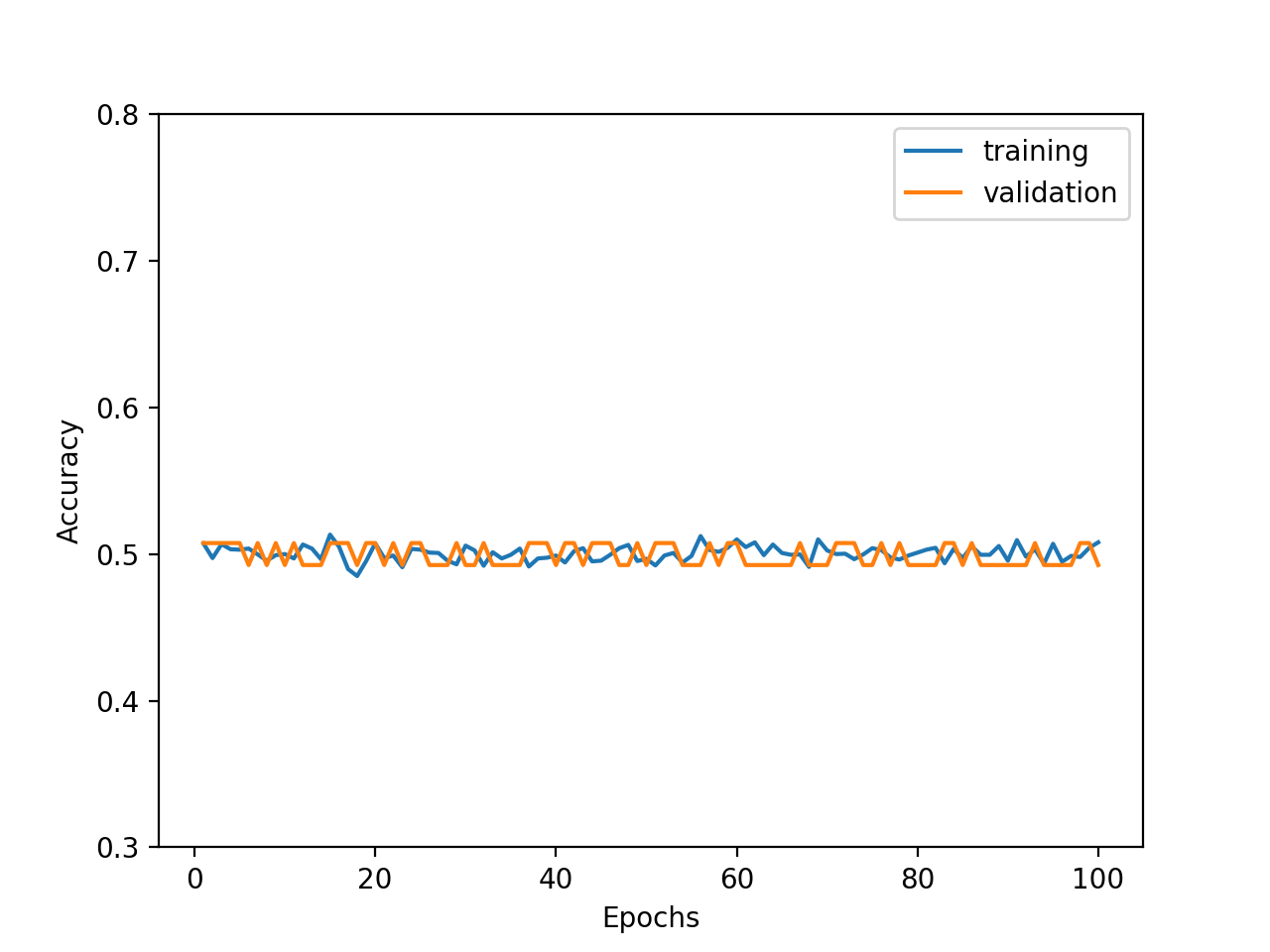
一方、特徴量の平均をずらし、0以上1未満の乱数値を+1000してみました。結果は、精度がほぼ0.5、すなわち2値分類としては全く学習されないことがわかりました。
全体的に、特徴量の正規化が大切であることがわかります。