More than 3 years have passed since last update.

いまさらECDSARECOVER

ECDSA

Last updated at 2021-09-03Posted at 2021-08-13

はじめに（Introduction）

Ethereum系のスマートコントラクトに若干関わる事になったのだが、
署名値の検証方法がBitcoinと異なる為、非常に混乱しました。

楕円曲線暗号の定義から、ECDSARECOVERの解説まで行います。
また、サンプルコード（JavaScript）も作成していきます。

楕円曲線暗号（Elliptic Curve Cryptography）

楕円曲線パラメータ（secp256k1）

楕円曲線は、有限体 $\mathbb{F}_p$ 上の曲線 $ y^2 = x^3 + ax +b $ を利用します。
secp256k1では以下のパラメータを使用します。

\begin{align*}
p =&\ \small{\texttt{FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F}} \\
=&\ 2^{256} − 2^{32} − 2^9 − 2^8 − 2^7 − 2^6 − 2^4 − 1 \\
a =&\ 0 \\
b =&\ 7 \\
\end{align*}

したがって、secp256k1は $y^2 = x^3 + 7 \pmod{p}$ の楕円曲線を使用します。
生成元 $G$ とその位数 $n$ は以下となります。
生成元は楕円曲線上の点（Point）で位数で循環します。

\begin{align*}
G =&\ \small{\texttt{04}} \\
&\ \small{\texttt{79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9
59F2815B 16F81798 }}\\
&\ \small{\texttt{483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8}} \\
n =&\ \small{\texttt{FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141}}\\
\end{align*}

点の加算、スカラー倍算の定義の元で、$G=nG+G$ が成り立ちます。
$p$ も $n$ も素数（Prime Number）となります。

サンプルコード（JavaScript）

// 楕円曲線演算（secp256k1）    

// 楕円曲線係数（ secp256k1 : y^2 = x^3 + 7　）
const b = 7n;
// 楕円曲線の位数
const p = BigInt('0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F');
// 生成元
const G = {
    x: BigInt('0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798'),
    y: BigInt('0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8'),
}
// 生成元の位数
const n = BigInt('0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141');

剰余演算（Modulo operation）

楕円曲線における点の加算やスカラー倍算、デジタル署名や検証の計算で扱う剰余演算を定義します。
位数を $p$ とします。
加算は、$x + y \equiv z \pmod{p}$ となります。
乗算は、$x \times y \equiv z \pmod{p}$ となります。
減算は、$x - y \equiv z \pmod{p}$ となりますが、JavaScriptの場合 $z$ が負の値となる場合があります。
この場合は正の値にする為、$z = p + z$ とします。（負の値で計算しても問題はありません。）
つぎに、べき乗を作成します。
べき乗の剰余なので、冪剰余を実装するのですが、$z \equiv x^y \pmod{p}$ のように簡単にはできません。
JavaScriptの場合、bigint型であっても上限が存在します。
「冪剰余 - Wikipedia#2.2 途中で剰余をとる」のロジックを利用します。
除算ですが、乗法逆元 $z \equiv x^{-1} \pmod{p}\ $ を算出し乗算と組み合わせる事で実現します。
$p$ が素数であれば、乗法逆元はフェルマーの小定理を応用して $z \equiv x^{p-2} \pmod{p}\ $ で計算できます。

サンプルコード（JavaScript）

// 剰余演算

/**
 * 加算（剰余演算）
 * @param {bigint} x 
 * @param {bigint} y 
 * @param {bigint} p 
 * @returns x + y mod p 
 */
function add(x, y, p) {
    return (x + y) % p;
}

/**
 * 減算（剰余演算）
 * 負値の場合、正値に変更
 * @param {bigint} x 
 * @param {bigint} y 
 * @param {bigint} p 
 * @returns x - y mod p
 */
function sub(x, y, p) {
    let z = (x - y) % p;
    if (z < 0n) {
        z += p;
    }
    return z;
}

/**
 * 乗算（剰余演算）
 * @param {bigint} x 
 * @param {bigint} y 
 * @param {bigint} p 
 * @returns x * y mod p
 */
function mul(x, y, p) {
    return (x * y) % p;
}


/**
 * 乗法逆元（剰余演算）
 * @param {bigint} x 
 * @param {bigint} p 素数
 * @returns x ^ -1 mod p
 */
function inv(x, p) {
    return pow(x, p - 2n, p);
}

/**
 * べき乗（剰余演算）
 * @param {bigint} x 
 * @param {bigint} y 
 * @param {bigint} p
 * @returns x ^ y mod p
 */
function pow(x, y, p) {
    let z = 1n;
    while (y > 0n) {
        if (y & 1n) {
            z = z * x % p;
        }
        x = (x * x) % p;
        y >>= 1n;
    }
    return z;
}

点の加算（Point Addition）

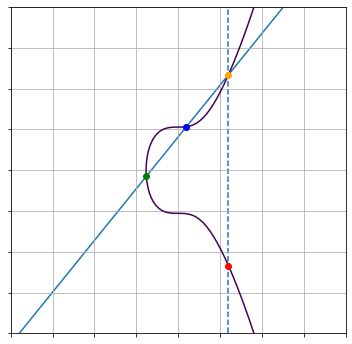
楕円曲線上の点の加算を以下のようにあらわす。

２点が異なる場合（P₁ ≠ P₂）

上の図で、緑の点を $P_1(x_1,y_2)$ 、青の点を $P_2(x_1,y_2)$、赤の点を $P_3(x_3,y_3)$ とします。
この時、$P_3 = P_1 + P_2$ とすると、$P_3$ は以下の式で求められます。

\begin{align*}
s&=\frac{y_2-y_1}{x_2-x_1}\\
x_3&=s^2-x_1-x_2\\
y_3&=s(x_1-x_3)-y_1\\
\end{align*}

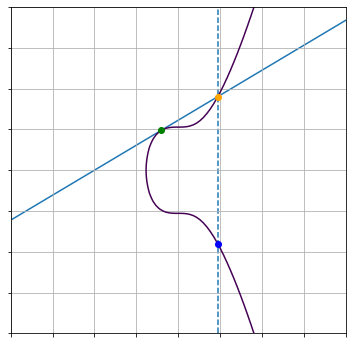
２倍算（P₁ = P₂）

同じ点を加算する場合を考えます。
上の図で、緑の点を $P_1(x_1,y_2)$ 、青の点を $P_3(x_3,y_3)$ とします。
この時、$P_3 = P_1 + P_1$ とすると、$P_3$ は以下の式で求められます。

\begin{align*}
s&=\frac{3x_1^2}{2y_1}\\
x_3&=s^2-2x_1\\
y_3&=s(x_1-x_3)-y_1\\
\end{align*}

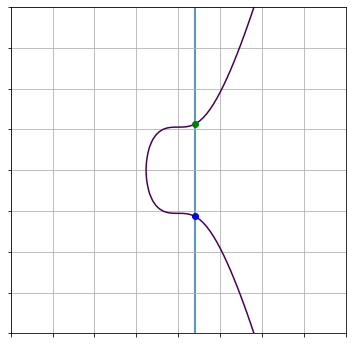
無限遠点（Point at infinity）

２点を通る直線を考えた時、上の図のように曲線と交わらない場合が考えられます。
この時、無限遠点 $I$ で交わる事とすると、以下のような点の加算ができます。

\begin{align*}
P = I + P =P + I\\
\end{align*}

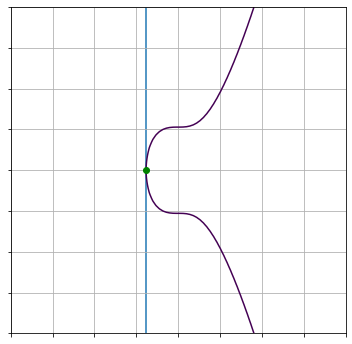
特殊な場合

上記のような点の場合、２倍算の結果は無限遠点となります。

以上を踏まえ点の加算のコードを作成します。
上記の図は全て実数での表現の為、連続したグラフになっていますが、実際は有限体なので連続なグラフとはなりません。

サンプルコード（JavaScript）

/**
 * 点の加算
 * @param {point} P1 
 * @param {point} P2 
 * @returns 点
 */
function addPoint(P1, P2) {
    if (P1.x == null && P1.y == null) {
        return P2;
    }
    if (P2.x == null && P2.y == null) {
        return P1;
    }
    let s = null;
    if (P1.x != P2.x) {
        // 異なる点
        // s = (P2.y - P1.y) / (P2.x - P1.x)
        s = sub(P2.y, P1.y, p) * inv(sub(P2.x, P1.x, p), p);
    } else {
        // 同一点
        if (P1.y != P2.y) {
            // P1 = -P2
            return { x: null, y: null };
        } else if (P1.y == 0n) {
            // 接線が垂直
            return { x: null, y: null };
        }
        // s = (3*P1.x^2) / (2 * P1.y)
        s = mul(3n, pow(P1.x, 2n, p), p) * inv(mul(2n, P1.y, p), p);
    }
    // P3.x = s^2 - P1.x - P2.x
    let x3 = sub(sub(pow(s, 2n, p), P1.x, p), P2.x, p);
    // P3.y = s*(P1.x - P3.x) - P1.y
    let y3 = sub(mul(s, sub(P1.x, x3, p), p), P1.y, p);
    return { x: x3, y: y3 };
}

スカラー倍算（Scalar Multiplication）

同じ点 $P$ を加算できるので、$P+P=2P\ $ とあらわします。
これを $k$ 回繰り返したものを、$kP$と表します。
これをスカラー倍算と呼びます。
実装するには、$k$ 回ループすれば良いように思えますが、secp256k1では非常に大きい数を使用します。
そこで、二進展開を用いる事で、$\log_2(k)$ 回で済むように工夫します。

サンプルコード（JavaScript）

/**
 * 点のスカラー倍算
 * @param {point} P 
 * @param {bigint} k 
 * @returns kP
 */
function mulPoint(P, k) {
    let Q = { x: null, y: null };
    while (k > 0n) {
        if (k & 1n) {
            Q = addPoint(Q, P);
        }
        P = addPoint(P, P);
        k >>= 1n;
    }
    return Q;
}

テスト（TEST）

secp256k1のテストデータ（secp256k1 Test Vectors）からテストを行います。

署名と検証（Sign and Verify）

Standards for Efficient Cryptographyの署名と検証についてみます。

署名（Sign）

Input
秘密鍵$\ x\ $、メッセージ$\ M\ $
Output
署名値$\ S=(r,s)\ $

Actions

一時的な$\ k\ $を選択します。（乱数など）
楕円曲線のスカラー倍算より、$R = kG\ ,\ R(x_R,y_R)\ $を生成します。
$\ r = x_R \pmod{n}\ $を計算します。
$\ e = \textit{HASH}(M)\ $メッセージをハッシュしそれを数値とします。
$s = k^{-1}(e + rx) \pmod{n}\ $左記の式で署名値を計算します。
$s=0\ $だった場合は1へ戻ります。
署名値$\ S=(r,s)\ $を返す。

The signer may replace (r, s) with (r, −s mod n), because this is an equivalent signature.
同等の署名であるため、署名者は (r, s) を (r, −s mod n) に置き換えることができます。

r は楕円曲線上の点における x 座標なので、y 座標の候補が2つになります。

検証（Verify）

Input
公開鍵$\ P(x_P,y_P)\ $、メッセージ$\ M\ $、署名値$\ S=(r,s)\ $
Output
署名値の有効（valid）または、無効（invalid）

Actions

署名値の$\ r\ $と$\ s\ $が$\ [1,n-1]\ $の範囲にあるか判定します。
範囲外の場合は**無効（invalid）**として処理を終えます。
$\ e = \textit{HASH}(M)\ $メッセージをハッシュしそれを数値とします。
$\ u_1=es^{-1} \pmod{n}\ $と$\ u_2=rs^{-1} \pmod{n}\ $を計算します。
$\ R=(x_R,y_R)=u_1G+u_2P\ $左記の計算を行います。
$\ R\ $が無限遠点の場合は**無効（invalid）**として処理を終えます。
$\ v=x_R \pmod{n}\ $を計算します。
$\ v = r\ $の場合は**有効（valid）として処理を終えます。
$\ v \ne r\ $の場合は無効（invalid）**として処理を終えます。

ECDSAPUBKEY, ECDSASIGN and ECDSARECOVER

Ethereum Yellow Paperにある、ECDSAPUBKEY、ECDSASIGN、ECDSARECOVERを実装してみます。
Ethereum系のスマートコントラクトでは ECDSASIGN で算出した署名値から、ECDSARECOVER を利用して公開鍵を復元する事で認証としているようです。

ECDSAPUBKEY

$\text{ECDSAPUBKEY}( p_r \in B_{32} ) \equiv p_u \in B_{64}$

Input
秘密鍵 $p_v$
Output
公開鍵 $p_u$

Actions

単純に生成元 $G$ を秘密鍵 $p_r$ でスカラー倍算して公開鍵 $p_u$ を求めます。

ECDSASIGN

$\text{ECDSASIGN}( e \in B_{32} , p_r \in B_{32} ) \equiv (v \in B_{1},r \in B_{64},s \in B_{64})$

Input
メッセージハッシュ $e$
秘密鍵 $p_v$
Output
署名データ $(v,r,s)$
　リカバリ識別子：$v \in \lbrace 27,28 \rbrace$
　$x$座標：$0 < r < n$
　署名値：$0 < s < n \div 2 + 1$

The value 27 represents an even y value and 28 represents an odd y value.
yの値が偶数ならば27、奇数であれば28とします。

rは楕円曲線のx座標なので、それを用いてy座標を求められますが、楕円曲線はx軸に対して対称な図形の為、y座標は2つ求められます。
奇素数pの有限体上での楕円曲線なので、y,-yならばどちらかが奇数、どちらかが偶数となります。
したがって、奇数が偶数かがわかれば一意にy座標が求められます。

Actions

通常の署名と同じように、一時的な $k$ を求めます。（乱数など）
生成元のスカラー倍算を行い、$R = kG$ とし$R(x_R,y_R)$ から $r = x_R$ とします。
$r$ が $0 < r < n$ でない場合、1からやり直します。
$x = p_v$ とし $s = k^{-1}(e + rx) \pmod{n}$ を求めます。
$s$ が $0 < s < n \div 2 + 1$ でない場合、$s=-s$ とし $R = -R$ とします。
$y_R$ が偶数の場合 $v=27$ とし、奇数の場合 $v=28$ とします。
署名データ $(v,r,s)$ を返します。

ep-155(https://github.com/ethereum/EIPs/blob/master/EIPS/eip-155.md)では、vに'CHAIN_ID'を含める仕様となっています。

ECDSARECOVER

$\text{ECDSARECOVER}( e \in B_{32} , v \in B_{1},r \in B_{64},s \in B_{64} ) \equiv p_u \in B_{64}$

Input
メッセージハッシュ $e$
リカバリ識別子 $v$
$x$座標 $r$
署名値 $s$
Output
公開鍵 $p_u$

Actions

$R(x_R,y_R)$ とした時、$x_R = r$ として、次のように$y_R$ を求めます。
$y_R = (x_R^3 + 7)^{\frac{p+1}{4}}$
$v$ が奇数（27）かつ $y_R\ $が奇数または、$v$ が偶数（28）かつ $y_R$ が偶数である場合、$y_R = p - y_R$ とします。
$Q = r^{-1}(sR - eG)$ を計算して、$Q$ を返します。

サンプルコード（JavaScript）

// ECDSA演算

/**
 * 公開鍵生成
 * @param {bigint} x 秘密鍵
 * @returns 公開鍵
 */
function ECDSAPUBKEY(x) {
    return mulPoint(G, x)
}

/**
 * 署名値生成
 * @param {bigint} e メッセージハッシュ
 * @param {bigint} x 秘密鍵
 * @returns 署名データ
 */
function ECDSASIGN(e, x) {
    let k = rnd32() % n;
    let R = mulPoint(G, k);
    let r = R.x;
    if (r >= n) {
        return ECDSASIGN(e, x);
    }
    // s = (e + xr) / k
    let s = mul(add(e, mul(x, r, n), n), inv(k, n), n);
    if (s == 0n) {
        return ECDSASIGN(e, x);
    }
    // 0 < s < n ÷ 2 + 1
    if (s > (n - 1n) / 2n) {
        s = n - s;
        R.y = p - R.y;
    }
    // v ∈ {27, 28} 
    // The value 27 represents an even y value and 28 represents an odd y value.
    let v = 27n + (R.y & 1n);
    return { v: v, r: R.x, s: s };
}

/**
 * 署名値から公開鍵取得
 * @param {bigint} e メッセージハッシュ
 * @param {bigint} v リカバリ識別子
 * @param {bigint} r x座標
 * @param {bigint} s 署名値
 * @returns 公開鍵
 */
function ECDSARECOVER(e, v, r, s) {
    let R = { x: r, y: null };
    // y = √(x^3 + 7)
    R.y = pow(add(pow(r, 3n, p), b, p), (p + 1n) / 4n, p);
    if ((v & 1n) == (R.y & 1n)) {
        R.y = p - R.y;
    }
    // Q = r^{−1}(sR − eG)
    let Q = mulPoint(addPoint(mulPoint(R, s), mulPoint(G, sub(n, e, n))), inv(r, n));
    return Q;
}

まとめ（Conclusion）

ソースコードは**Githubにあります。
デモはここ**にあります。

$x_R=r$ から $R(x_R,y_R)$ が復元できれば、公開鍵も復元できる事がわかりました。
問題としては、$x_R$ は有限体 $\mathbf{F}_p$ 、その他は有限体 $\mathbf{F}_n$ の為、微小な差があります。
その為、かなりの低確率で候補がもう１つあるみたいです。（詳細は以下を参照ください。）
Standards for Efficient Cryptography / SEC 1: Elliptic Curve Cryptographyの「4.1.6 Public Key Recovery Operation」

参考（References）

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

いまさらECDSARECOVER

はじめに（Introduction）

楕円曲線暗号（Elliptic Curve Cryptography）

楕円曲線パラメータ（secp256k1）

剰余演算（Modulo operation）

点の加算（Point Addition）

２点が異なる場合（P1 ≠ P2）

２倍算（P1 = P2）

無限遠点（Point at infinity）

特殊な場合

スカラー倍算（Scalar Multiplication）

テスト（TEST）

署名と検証（Sign and Verify）

署名（Sign）

検証（Verify）

ECDSAPUBKEY, ECDSASIGN and ECDSARECOVER

ECDSAPUBKEY

ECDSASIGN

ECDSARECOVER

まとめ（Conclusion）

参考（References）

２点が異なる場合（P₁ ≠ P₂）

２倍算（P₁ = P₂）