はじめに
前回の記事で紹介した密度推定の手法を応用して、データのサンプリングを行ってみます。
$F(x)=P(X\leq x)$を学習させたモデルをもとに、この逆関数$G(y)$を同様のニューラルネットで学習させます。
$[0, 1]$の一様分布から得られた$y$に対して、$F(G(y))$がyに近づくようにオートエンコーダ的な学習を行えばいいわけです。損失関数にはベルヌーイ分布を仮定した負の対数尤度(chainer.functions.bernoulli_nll())を使います。
学習後、サンプリングを行うには$[0, 1]$の一様分布から得られた$y$で$G(y)$を計算させれば良いです。
一次元混合ガウス分布
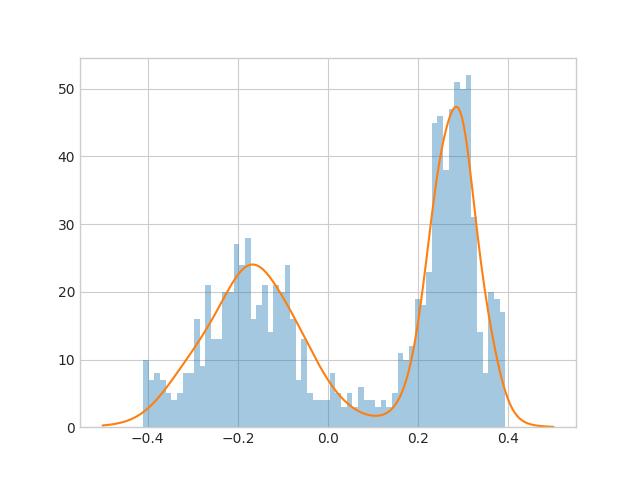
オレンジ色の実線が学習済みの$P(X)$で、青の棒グラフが今回のサンプリング結果です。
$P(x)=0$ 付近と、$P(x)=1$ 付近ではうまくサンプルが得られていないようです。
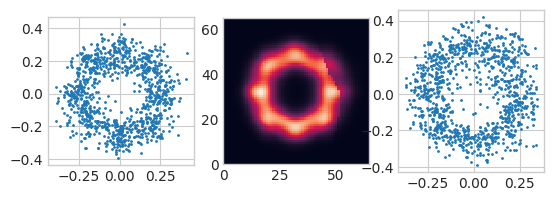
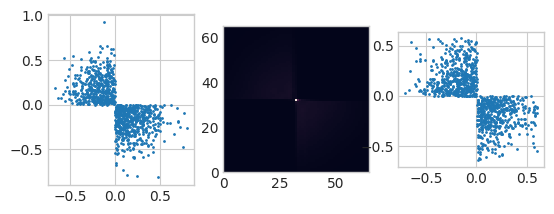
二次元混合ガウス分布
左から順に、元データ、$P(X)$の学習結果、今回の手法によるサンプリング結果です。
$P(X)$の学習結果に影があらわれていますが、Min-Max Poolingが悪さをしているようです。このプーリングは不要なのかもしれません（要調査）。
二次元切断(?)ガウス分布
$P(X)$のヒートマップ上ではうまく行っていないように見えましたが、今回の結果を見ると意外と形は取れているようです。