はじめに
私は力学屋が本業ですが、2年ほど前から仕事で機械学習を触っています。なんとか機械学習を活用したいなと思っているのですが、機械学習は統計ベースのため力学的背景を持っていないという欠点を拭えずにいました。そんな中Physics-informed Neural Network(PINN)という手法を見て「これなら欠点解決じゃん!」とこの手法に飛びつきました。今回は地盤分野の基礎的な解析である一次元圧密沈下解析を(PINN)で解いてみたいと思います。
圧密沈下とは
皆さんの足の下に存在する地盤は土粒子と土粒子の間を埋める水(間隙水)、空気で構成されています。更に土粒子の細かさによって粘性土、砂、礫、岩に分けられます。一方、地盤に荷重がかかると土粒子が密になり、体積が減少します。これが地盤沈下です。一般的に粘性土は透水係数が非常に小さいことから、載荷してから沈下が終了するまでに非常に長い時間がかかります。これを圧縮と区別して圧密と呼びます。
https://shinsa-hosho.jp/basic-knowledge-of-jiban/mechanism-of-ground-subsidence
地盤上に建物を建てる際にはこの圧密沈下でどの程度沈下が生じるか、いつまで沈下が生じるかが重要な問題となります。これを地盤調査を行いその結果を用いて設計で沈下解析を行います。解析には圧密沈下を表現するモデルが必要となりますが、最も簡単なものにTerzaghiの圧密理論があります。これは荷重を載荷した際に瞬間的に過剰間隙水圧が発生し、それが消散することで沈下が発生するという仮定のもと、過剰間隙水圧の消散時間を計算するものです。実際の設計にも使用されています。
圧密理論は以下の熱伝導型偏微分方程式で表されます。
\frac{\partial u}{\partial t} = cv\frac{\partial^2 u}{\partial z^2}
ここで、u:過剰間隙水圧、t:時間、z:地表面からの距離、cv:定数(圧密係数と呼ぶ)です。
Physics-informed Neural Networkとは
PINNは物理法則を活用してデータを用いずにNeural Networkの学習を行うという手法です。これまでNeural Networkで数値解を求めようとすると、データドリブンという手法が主かと思います。これは、別途数値解析で求めた解析解をデータとして入力し、データから入力と出力の関係をNeural Networkで近似するという手法になります。一方、PINNはデータの代わりに支配方程式と境界条件を入力し、それぞれの式が0になるようにNeural Networkで近似するという手法になります。自由落下を例にすると、下図のように初期・境界条件と微分方程式(運動方程式)によるロスを計算し、そのロスを最適化することでNeural Networkの解を算出します。
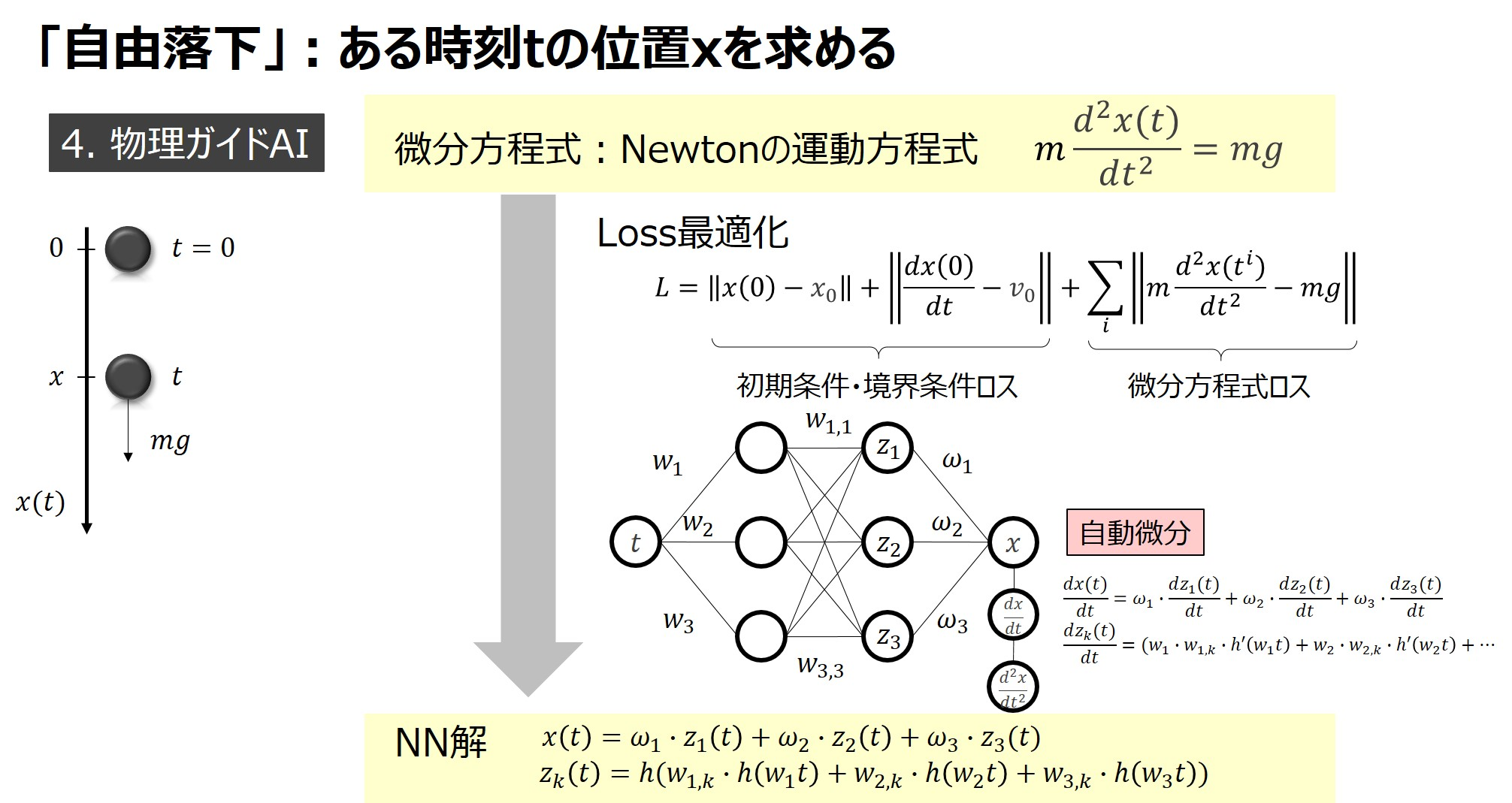
https://qiita.com/nnnnnnn/items/df62e9fb0ec999df96a2
データドリブン法はデータの範囲外の精度が保証されない、Neural Networkの解が力学的根拠を持たないという欠点がありますが、PINNは構成式が対応できる範囲であれば力学的根拠のある解を算出できるという利点があります。
PINNで圧密方程式
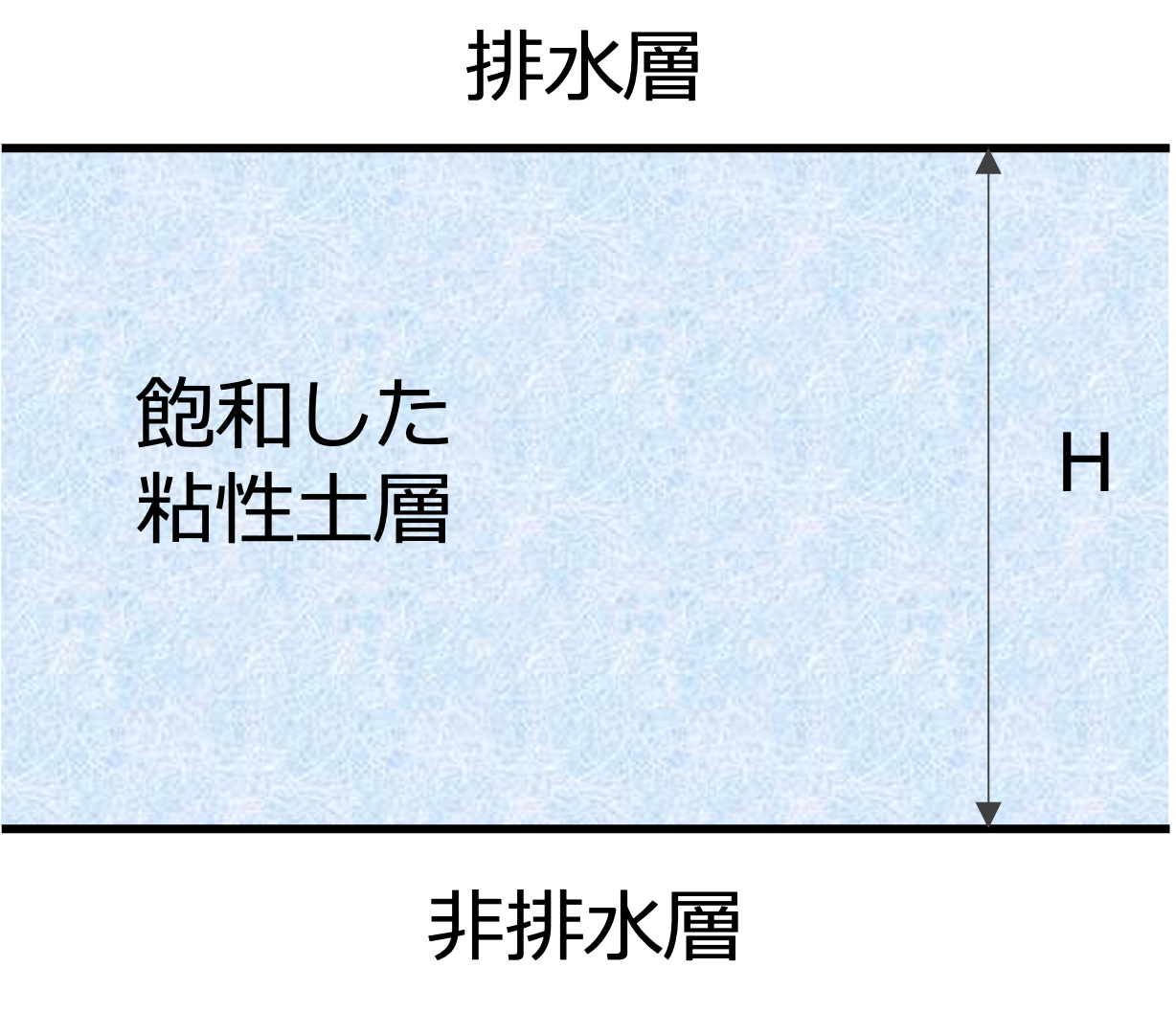
PINNで圧密方程式を求めようとすると以下のようになります。まず、下図のように仮想的な地盤を考えます。上部は排水できますが、下部は岩等の不透水層になっているとします。
境界条件は上部では過剰間隙水圧が発生しないのでu=0となります。また、不透水層では境界条件は以下のようになります。
\frac{\partial u}{\partial z} = 0
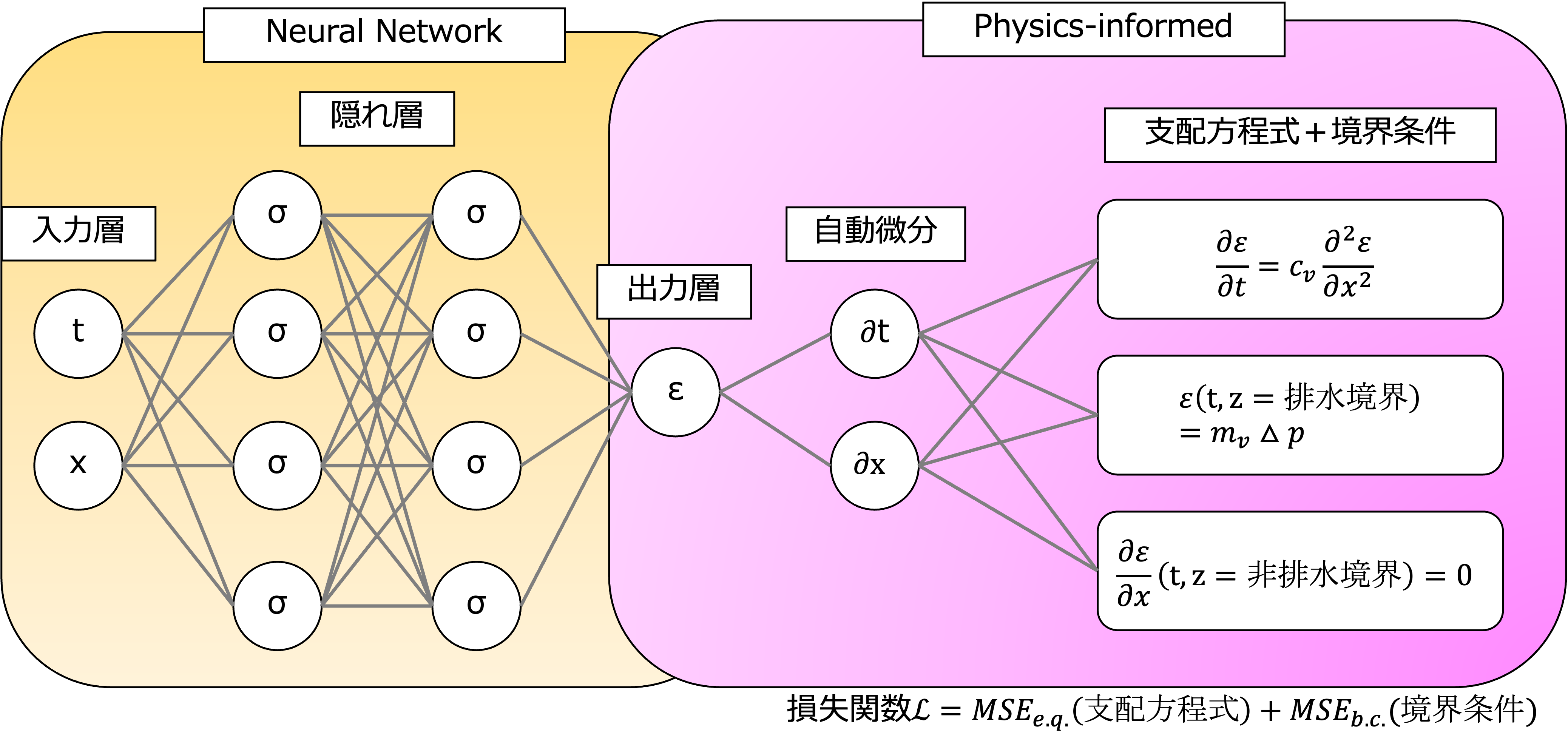
最後に初期条件はu(z=H)=p(上載荷重)になります。以上を考慮すると下図のような手法でNeural Networkの解を求めることになります。
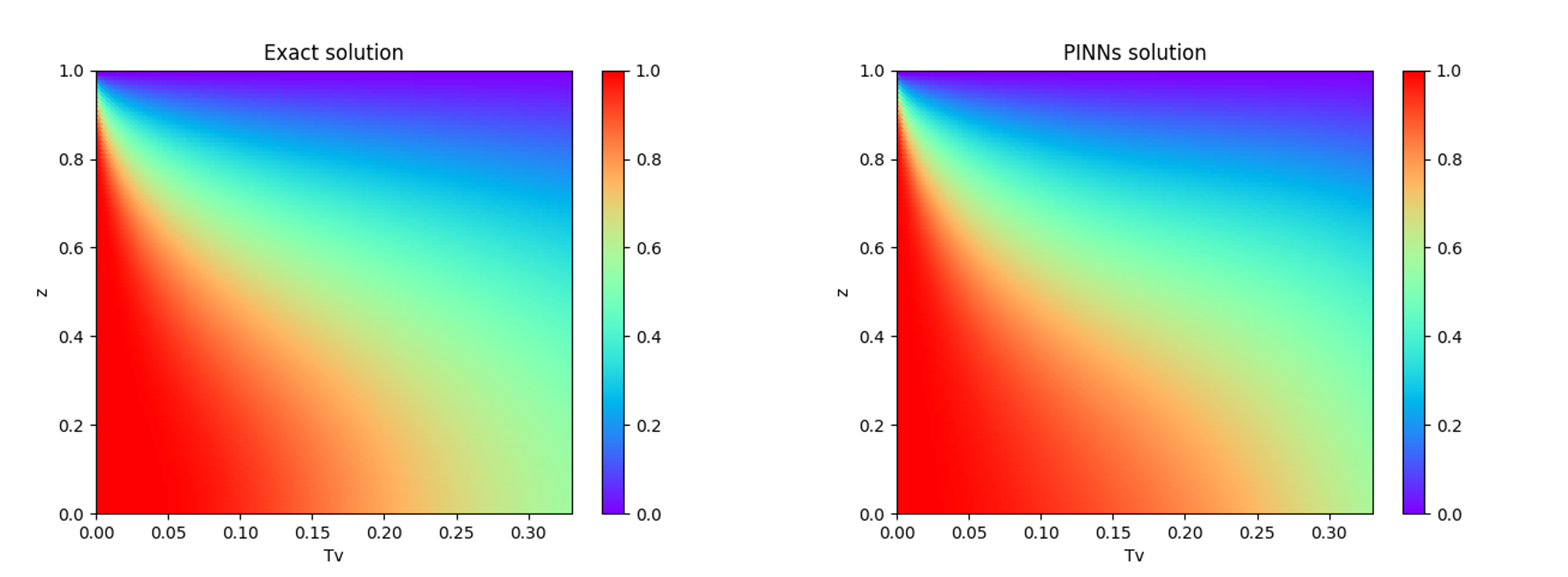
試しに実際に計算した結果を以下に示します。理論解の求め方は土質力学の教科書等を読んでください。計算結果は理論解とほぼ一致しています。PINNが解析手法として有用であることが伺えます。
おわりに
PINNについての論文をいくつか読んでみましたが、現状では一次元がメインで二・三次元の実用例はほぼないように思います。一次元だけでは数値解析の代わりにはなりえないのでまだまだ研究が必要そうです。