はじめに
みなさん、こんにちは。
近年、Deep Learningを使った物理シミュレーションの高速化の研究が活発に行われています [1]。
特に、2020年5月に発表されたNVIDIA SimNet™では、Deep Learningを用いた物理シミュレーションのツールキットがearly accessながら提供開始されており、実用化に向けたフェーズに入っていると言っても良いと思います [2]。
NVIDIA SimNet™におけるDeep Learningを使った物理シミュレーションの特徴の一つに**「学習データが必ずしも必要ない」**というものがあります。
これは物理法則(微分方程式)を知識として活用することで学習データを使わずにニューラルネットワークを学習するという特徴であり、学習データを必須とする従来のニューラルネットに比べて大きな違いがあると言えます。この特徴については、Physics-Informed Neural Networksという論文に詳細が記述されています [3]。
論文Physics-Informed Neural Networksに記載された例は、流体力学のベースであるナビエ・ストークス方程式(偏微分方程式)などで説明も複雑なのですが、本記事では、物理法則(微分方程式)を活用するPhysics-Informed Neural Networksとは何か、これまでの技術とは何が違うのかを分かりやすく説明するために、最もシンプルな物理現象である自由落下を例に説明してみたいと思います。
簡略化した説明ですので、厳密な説明とは異なる部分もあるかもしれませんが、ご了承いただけますと幸いです。
これまでの技術と何が違うのか?
これまで微分方程式を解く方法として、下記3つのアプローチがありました:
- 代数解法
- シミュレーション
- Data-Drivenアプローチ
簡単化のため、**「自由落下において、ある時刻tにおける位置xを求める」**という例を使い、それぞれ3つのアプローチを紹介した上で、Physics-Informedアプローチについても説明したいと思います。
1. 代数解法
微分方程式を解くために、代数的に陽に解く方法が代数解法です。自由落下の場合、重力加速度$mg$の力がかかります。Newtonの運動方程式で表すと、$m\frac{d^2x(t)}{dt^2}=mg$です。これを代数的に解くと、$x(t)=\frac{1}{2}gt^2+v_0t+x_0$です。ここで、$t=0$における速度、位置を$v_0$、$x_0$で表しています。代数解法は、陽に解けない偏微分方程式など、解けない問題があることが課題です。

2. シミュレーション
代数解法で解けない場合には、数値解法であるシミュレーションを使います。Newtonの運動方程式までは同じですが、数値解法では時間・空間を離散的に分割し、微分方程式を参照しながら数値的に算出していきます。精度(何次の微分まで考慮するか)によって方法は異なりますが、例えば最も簡単にはEuler法を使って、次のタイムステップにおける速度・位置を順番に求めます。下図の$\Delta$はタイムステップの間隔(単位は[sec])を表しています。これにより、各時刻$t$における位置$x$を数値的に算出することができます。シミュレーションは**順番に計算する必要がある(任意の時刻$t$における位置$x$を求めることができない)**という課題があります。

3. Data-Drivenアプローチ
任意の時刻$t$における位置$x$を直接求めることができないという課題を解決するために、近年Deep Learningを用いたData-Drivenアプローチが提案されています。これは、シミュレーションで求めた数値解(入力と出力のセット)を基に、入力と出力の関係をNeural Networkで近似するというものです。下図のNeural Networkの構造は簡単化のためかなり単純化されていますが、そのような構造の場合でも、基本的には入力$t^i$をNeural Networkに入れて出力された予測値$x(t^i)$と、シミュレーションで求めた数値解$x_i$の誤差が最小となるようなLossを設計して、Neural Networkの重みを学習します。これにより、任意の時刻$t$における位置$x$を出力できることになります。本アプローチは、シミュレーションによる数値解などの学習データが必要、さらに**学習データの範囲内でないと性能が保証されない(近似精度が低い)**という課題があります。
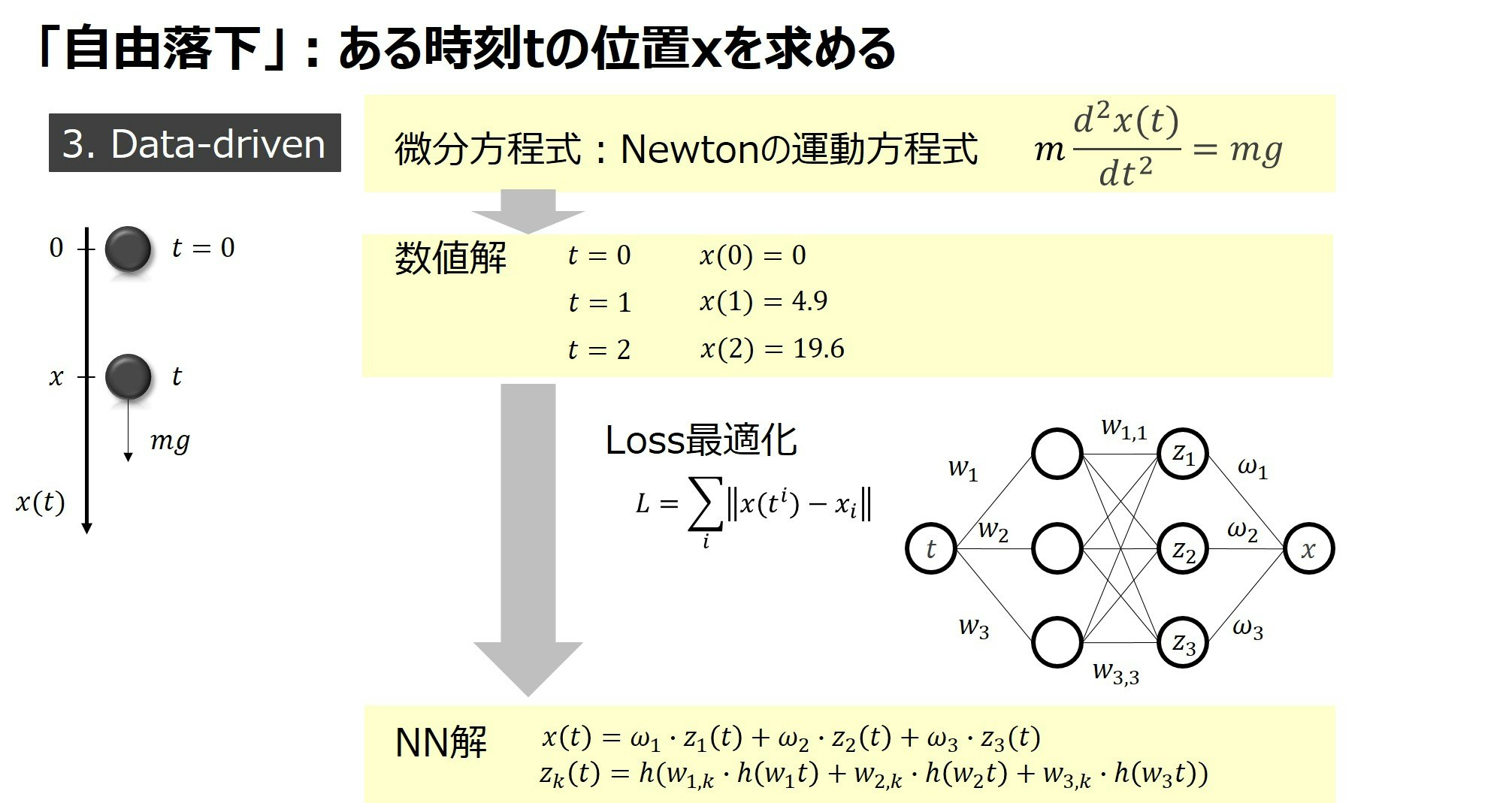
そして、学習データが必要という課題を解決するアプローチが、Physics-Informedアプローチです。
新しいアプローチ
4. Physics-Informedアプローチ
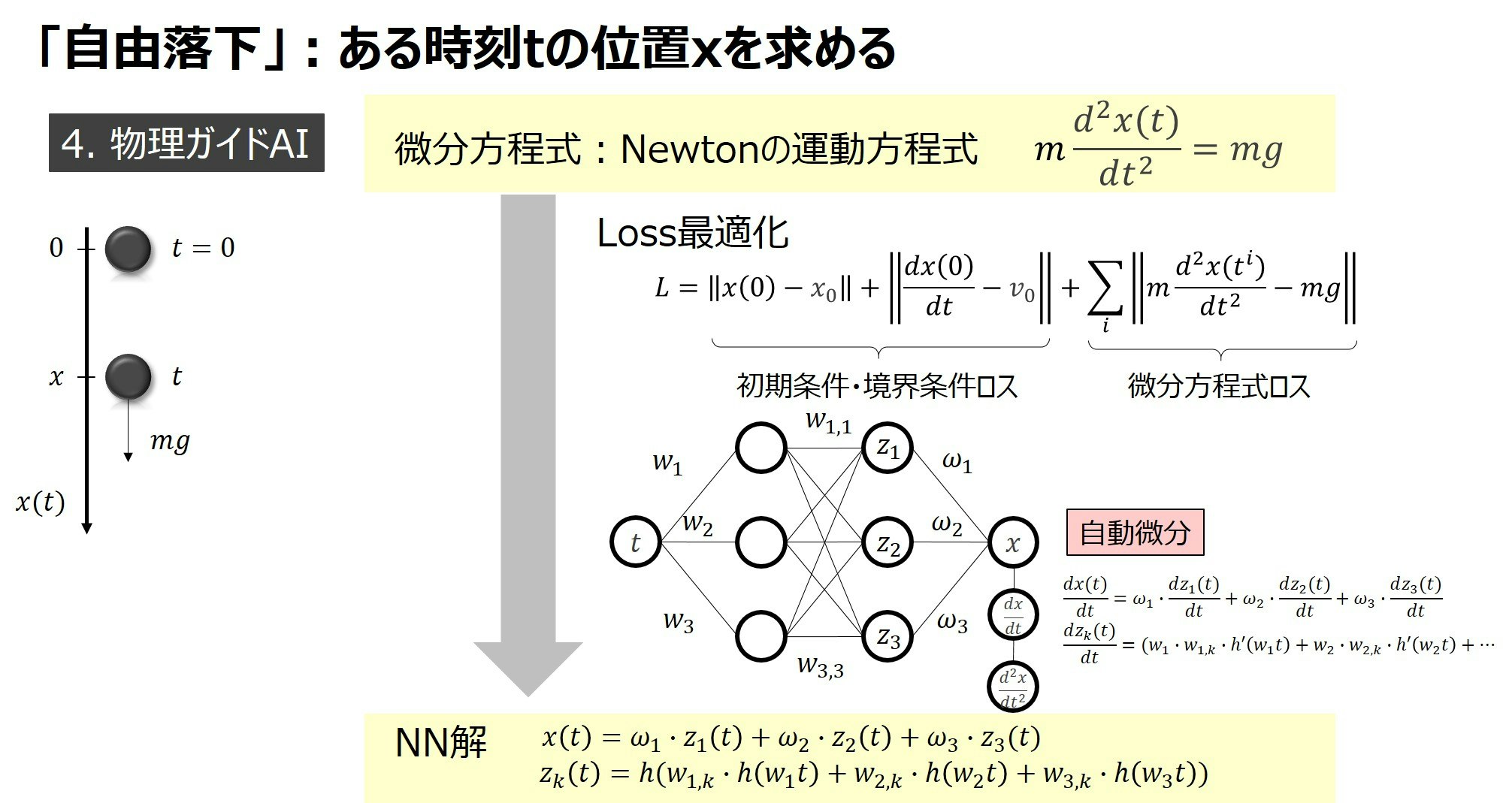
本アプローチもNeural Networkを使ったものですが、Data-DrivenアプローチとはLossが異なります。本アプローチでは学習データは使わず、初期条件・境界条件のロスと微分方程式のロスを使います。
初期条件・境界条件のロスとは時刻$t=0$において位置$x(0)$や速度$\frac{dx(0)}{dt}$を初期条件に合わせるためのロスです。自由落下の場合には境界条件は出てきませんが、流体力学のナビエ・ストークス方程式では境界条件(物体がどこにいるか、形状はどのようなものかなど)のロスが必要になります。初期条件・境界条件のロスが学習データと言えばそう言えるかもしれませんが、初期条件・境界条件は問題設定の際に与えられていることがほとんどなのでシミュレーションをする必要はありません。
もう一方のロスである微分方程式のロスですが、これはNewtonの運動方程式をそのまま使い、イコール$0$となるようにロスを設計します。ここで二次微分$m\frac{d^2(t^i)}{dt^2}$をどのように求めるかですが、出力$x$に対する入力$t$の(偏)微分として、自動微分の機能を使って算出します。Neural Networkの解$x(t)$自体は、ネットワーク構造が決定すると下図のように重み$\omega, w$を使って書き下すことができます。重み自体はロスの最適化によって求めます。Neural Networkの解の一次微分$\frac{dx(t)}{dt}$も、下図のように自動微分の機能を使い、重み$\omega, w$を使って表すことができます。二次微分も同様に算出することができます。その結果、自動微分の式を使って微分方程式のロスを計算することができます。
ここで、Physics-Informedアプローチのメリット、デメリットを簡単に整理したいと思います:
- メリット
- 学習データを準備する必要がない。
- 学習データのロスを使わず微分方程式のロスを使っているので、学習データに依存せず汎用性が高い。
- 微分方程式を直接ロスとして使っているので、離散誤差を原理的に含むシミュレーションより精度が高い(かもしれない)。
- デメリット
- 微分方程式のロスはData-Drivenアプローチより収束が遅い(傾向のようである)。
- 初期条件・境界条件のロスを最適化するため、初期条件・境界条件が変わると再学習する必要がある。
デメリットの2つ目は特に影響が大きいかもしれません。流体力学の例では、物体周辺の速度分布や圧力分布などを推定する場合、物体の形状が境界条件となりますが、物体の形状を変えて推定したい場合には再学習が必要になります。そのため、物体の最適な形状を探索したい場合などには計算時間のかかるアプローチとなります。
ただ、Physics-Informedアプローチでは、入力として状態変数だけでなくパラメータ(自由落下の場合は初速度$v_0$など)を入れて学習することもできます。この場合は、異なるパラメータでの再学習は必要なくなるのですが、入力できるパラメータには制約があります。パラメータとして入力できるのは、数値で表せるものに限られており、曲線の境界条件や、一般的なNeural Networkで扱われるようなクラスのような概念のパラメータなどは入力できないようです。そのため、現状では、複雑な境界条件のある問題設定の場合は再学習が必要になると言えると思います。
おわりに
本記事では、物理法則(微分方程式)を使って学習データなしでモデル構築可能なPhysics-Informed Neural Networkを紹介しました。学習データを必要としない、また、汎用性が高いなど、従来のNeural Networkにない特徴を持っている一方、初期条件や境界条件が変わる場合には再学習が必要という実用性の課題もあり、これからの進展を注意深く見ていきたいと思っています。
最後までお読みいただき、ありがとうございました。
参考文献
[1] 深層学習を使った物理シミュレーションの高速化に関する記事です:
[2] NVIDIA SimNetを紹介した記事や論文です:
- NVIDIA SimNet の紹介
- Oliver Hennigh et.al, "NVIDIA SIMNET™: AN AI-ACCELERATED MULTI-PHYSICS SIMULATION FRAMEWORK", arxiv, 2020.
[3] Physics-informed Neural Networksの代表的な論文です:
- Maziar Raissi, Paris Perdikaris, and George E. Karniadakis, "Physics-Informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations", Journal of Computational Physics, 2019.