【秘密計算】最古のMulti-party Computationプロトコル「Yao's Garbled Circuit」とは

はじめに

この記事では、最古のMulti-Party Computation（以下MPC）プロトコルである、「Yao's Garbled Circuit」の仕組みを紹介していきます。

Yao's Garbled Circuit 概要

Yao's Garbled Circuit は1982年にAndrew Yao 氏が発表した、2者間での初めてのMPCプロトコルです。 2人の参加者が提供する秘密データ$x, y$ をお互いに知られることなく、関数$f(x, y)$ の実行結果を得ることができます。関数$f(x, y)$ は次節に説明するGarbled Boolean Circuit によって構成されます。また、その特徴をまとめると以下になります。

特徴

• ブール回路
• Semi-Honest Security
• 2 Party Computation

ブール回路とは、関数の構成に論理ゲートを用いる場合を指しています。また、Semi-Honest Security とは、参加者がプロトコルから逸脱しない場合においてセキュアであることを示しています。最後に、2 Party Computation とは、参加者が2人である場合のMPCであることを示しています。

Garbled Boolean Gate

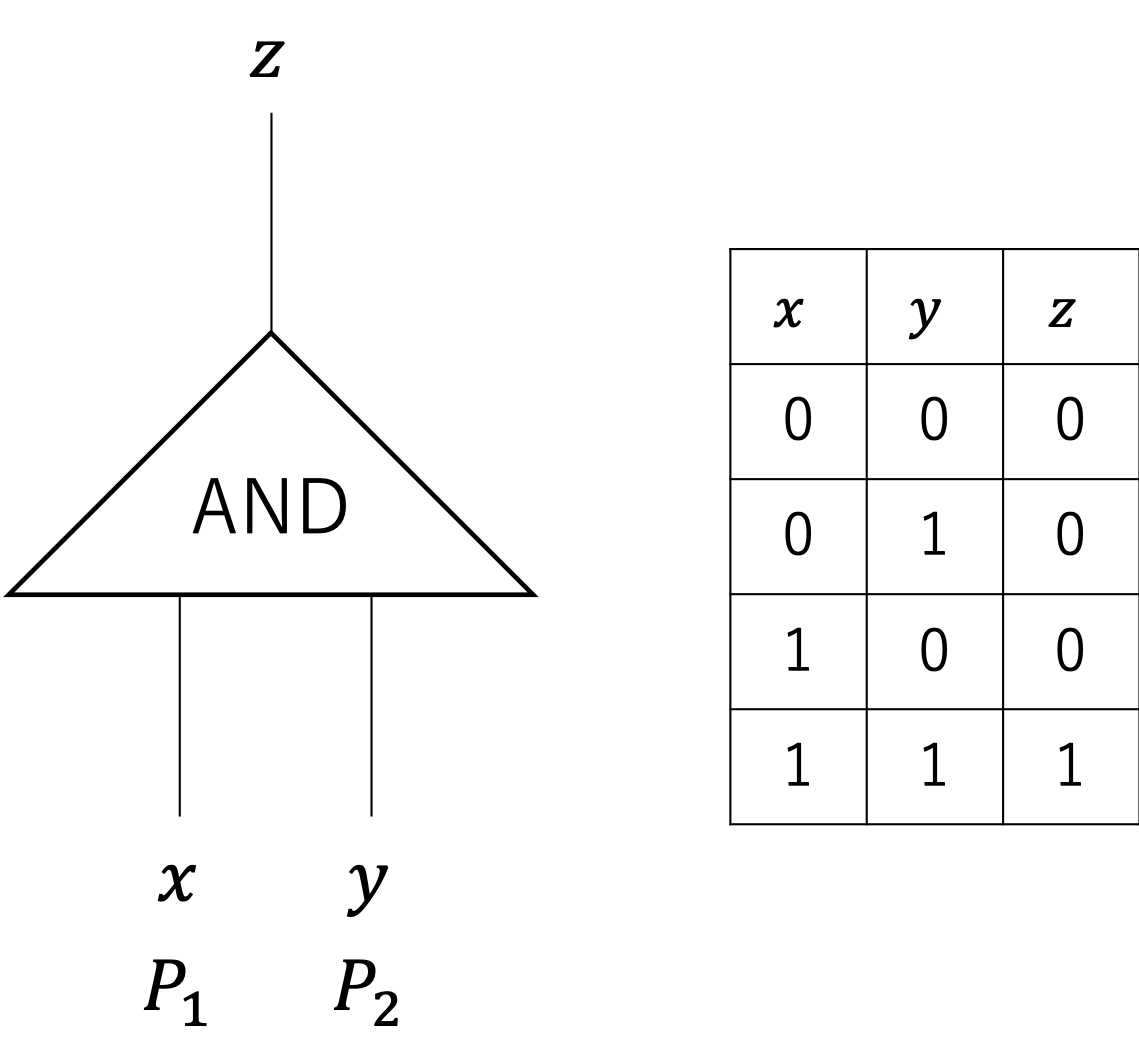
関数$f(x, y)$ を構成する論理ゲートは、2つの入力ビット$x, y$ を知られずに、計算結果$z$ を出力することを目指します。このような論理ゲートのことをGarbled Boolean Gate(GBG) と定義します。以後は論理ゲートとして以下のようなANDゲートを想定します。

$P_1$と$P_2$は参加者、$x, y$ はそれぞれの参加者が入力する1ビットの秘密情報、$z$ はAND ゲートの出力ビットを表しています。

Garbled Computation Table

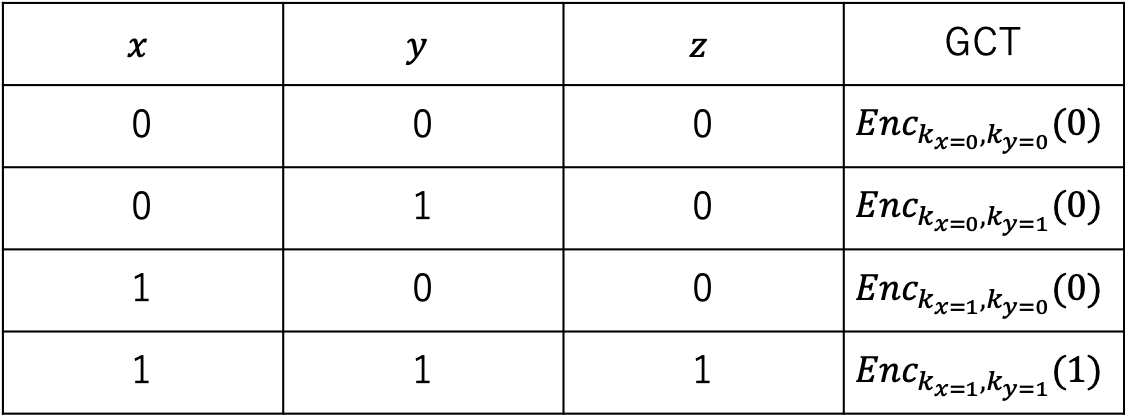
上記のGBGを実現するために、Garbled Computation Table(GCT)という表を導入します。Yao's Garbled Circuit では論理ゲートの計算を表によって実現することで、入力値$x, y$ を秘密にしたまま計算結果を出力します。以下にAND ゲートのGCTを示します。

ここで、$Enc()$は添字の鍵によって暗号化する関数を示しています。また、$k$ は$x, y$ の値に対応する鍵であり、添字が$x, y$ のそれぞれの入力ビットの値に対応しています。つまり、$P_1$と$P_2$の入力ビットそれぞれに対応した鍵であることを示しています。この時GCTは、AND ゲートの出力結果である$z$ の値を、それぞれに対応する$x, y$ の鍵$k$ で暗号化したものを表しています。

ANDゲートの計算結果は、$x, y$ それぞれの対応する鍵を用いてGCTを復号することで得られます。例えば、$x = 0, y = 1$ に対応する鍵$k_{x=0}, k_{y=1}$ を獲得した場合は、$z = 0$ を復号することができます。以下にプロトコルの手順を示します。

手順

1. $P_1$ が全ての鍵$k$ を生成しAND ゲートに対応するGCTを作成する
2. $P_1$はGCTの行の並びをシャッフルする
3. $P_1$ は$P_2$ に作成したGCT を送信する
4. $P_1$ は$P_2$ に自身の入力ビットに対応した鍵$k_x$ を送信する（$P_2$ にはどちらのビットに対応した鍵であるかは分からない）
5. $P_1$ は$P_2$ にOblivious Transfer を用いて$k_{y=0}, k_{y=1}$ を送信する（Oblivious Transfer は後述する）
6. $P_2$ はGCT, $k_x, k_y$ を用いて計算結果$z$ を復号する
7. $P_2$ は$P_1$ に計算結果$z$ を送信する

ここで、Oblivious Transfer は受信者の受け取った値が送信者には分からない通信方法です。また、受信者は受け取った値しか知ることができません。したがって、$P_1$は$k_{y=0}, k_{y=1}$ のどちらを$P_2$ が受け取ったのかを知ることがなく、$P_2$ は受け取った鍵の値しか知ることはできません。また、GCTをシャッフルすることで、どの行がどの入力に対応しているのかを$P_2$は知ることができません(garbled は「シャッフルされた」という意味です)。結果的に、$P_2$ は$P_1$ から$k_x, k_y$ の2つの鍵を入手することができたため、GCTの適切な行を復号しz の値を得ることができました。

上記のプロトコルにより、$P_1, P_2$ の入力ビット$x, y$ の値が相手に知られることなく、AND ゲートの計算結果を得ることができました。さらに、GCTはAND ゲート以外の任意の論理ゲートに適用できるため、任意の関数$f(x, y)$ をブール回路を用いて実現することができます。

まとめ

Yao’s Garbled Circuit は最古のMPCプロトコルであり、Semi-Honest Security 、2 Party Computation 、ブール回路という特徴を持っています。そして任意の関数$f(x, y)$ を$x, y$ を秘密にしたまま計算可能であり、Garbled Boolean Gate とGarbled Circuit Table を用いて参加者$P_1$ と$P_2$ の間でMPCを実現しています。

参考文献

#Happy Hacking !