本記事の概要
Flow-based Deep Generative Models
を参考に、Flow, Normalizing-Flow とは何か、についての理論的な部分のみサマリとして残す。よって、具体的なモデル(具体的な深層学習モデルの適用)についての解説・サマリは省略した。
理解をするにあたっての参考になるように、いくつか数学的な補足(式の導出、証明)を追加した。
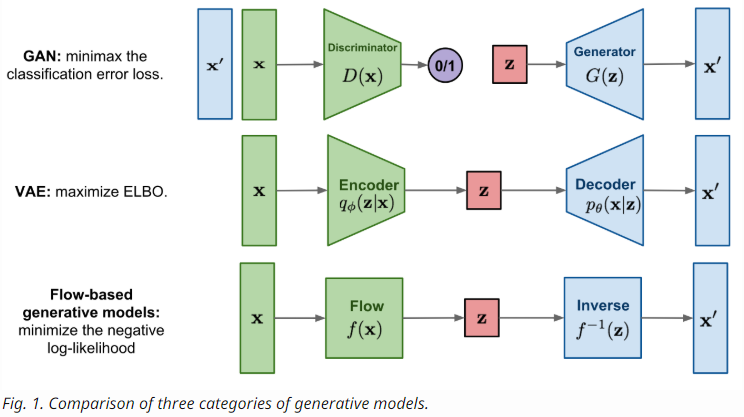
Types of Generative Models
- GAN
- ディスクリミネータは、ジェネレータが生成した偽物を見抜くための判別を学習
- mini-max ゲームとしての学習を教師なしで
- VAE
- ELBOを最大化することで、対数尤度を最大化
- Flow ベース
- 可逆変換の系列により生成
- GAN、VAEとは異なり、陽に $p(x)$ を学習
- 損失関数は、負の対数尤度
What is Normalizing Flows?
- 良い密度(分布)推定は、良い応用だが非常に難しい
- DLでは、BP(誤差逆伝播法)が必要
- 埋込分布(事後分布 $p(z|x)$)は、微分の計算が十分簡単で効果的にできる必要がある
- これが潜在変数の生成モデルで、正規分布が良く使われる理由
- 現実世界の分布は、正規分布よりも一般に複雑
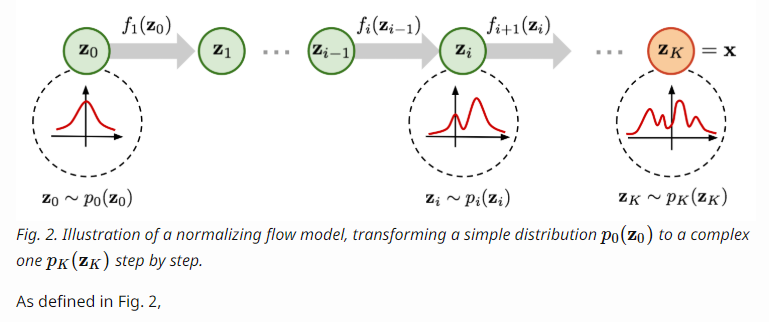
- NF(Normalizing Flow) モデルは、よりよい分布の近似を提供する
- NFは、シンプルな分布から複雑な分布に変換
- この変換は、可逆変換の連鎖(合成写像)で実現
- 変換の連鎖により、繰り返し変数に新しい変数を代入
式でモデル化すると以下のよう表せる。
$$
\begin{align}
z_{i-1} &:\sim p_{i-1}(z_{i-1}) \
z_i &:= f_i(z_{i-1}) \
i.e.~ z_{i-1} &= f_i^{-1}(z_i) \
p_i(z_i) &:= p_{i-1}( f_i^{-1}(z_i) ) \left | \det \frac{df_{i}^{-1}}{dz_i} \right | \
i.e.~ p_i(z_i) &:= p_{i-1}( z_{i-1} ) \left | \det \frac{df_{i}^{-1}}{dz_i} \right | \
\end{align}
$$
ここで、$\det \frac{df_{i}^{-1}}{dz_i}$ が定義できる条件は、$z_{i-1}$ と $z_i$ の次元が同じ、つまり $z_{i-1}, z_i \in \mathbb{R}^n, f_i, f_i^{-1} : \mathbb{R}^n \rightarrow \mathbb{R}^n$ が前提条件であることに注意する。
また、$\left | \det \frac{df_{i}^{-1}}{dz_i} \right |$ は、分布(積分)の変数変換にも登場することに留意する。
さて、$z_i$ について解くと、
$$
\begin{align}
p_i(z_i)
&= p_{i-1}(z_{i-1}) \left | \det \frac{df_{i}^{-1}}{dz_i} \right | \
&= p_{i-1}(z_{i-1}) \left | \det ( \left ( \frac{df_{i}}{dz_i} \right )^{-1} ) \right | & \because inverse~ function~ theorem \
&= p_{i-1}(z_{i-1}) \left | \left ( \det \frac{df_{i}}{dz_i} \right )^{-1} \right | & \because Jacobians~ of~ invertible~ function \
\log p_i(z_i)
&= \log p_{i-1}(z_{i-1}) - \log \left | \left ( \det \frac{df_{i}}{dz_i} \right ) \right | \
\end{align}
$$
Inverse Function Theorem
Inverse Function Theorem は、逆関数のヤコビ行列が、元の関数のヤコビ行列の逆元(逆行列)になることに一致する、ことを主張する定理
式で表すと、以下のように表せる。
$$
\begin{align}
J_{f^{-1}} &= J_f^{-1} \
\end{align}
$$
まずは、一変数について整理しておく。
$y = f(x)$, $x = f^{-1}(y)$ の時、
$$
\begin{align}
\frac{df^{-1}(y)}{dy}
&= \frac{dx}{dy} \
&= \left ( \frac{dy}{dx} \right ) ^{-1} \
&= \left ( \frac{df(x)}{dx} \right ) ^{-1} \
\end{align}
$$
一般に拡張することを考える。
$$
J_f = \left [ \frac{\partial y_j}{\partial x_i} \right ]_{j, i} \
$$
$$
J_{f^{-1}} = \left [ ( \frac{\partial y_j}{\partial x_i} ) ^{-1} \right ]_{i, j} \
$$
のようにヤコビ行列を表記し、$J_f J_{f^{-1}}$ を計算する。
$$
J_f J_{f^{-1}} = \left [ \sum_{i} \frac{\partial y_j}{\partial x_i} ( \frac{\partial y_k}{\partial x_i} ) ^{-1} \right ]_{j, k}
$$
$$
= \left [ \sum_{i} \frac{\partial y_j}{\partial x_i} \frac{\partial x_i}{\partial y_k} \right ]_{j, k}
$$
$$
= \left [ \frac{\partial y_j}{\partial y_k} \right ]_{j, k} \
$$
$$
= \left [ \delta_{j, k} \right ]_{j, k} \
$$
$$
= I_n ~ (identity~ matrix) \
$$
ここで、
$y_k \rightarrow (x_1, ..., x_m) \rightarrow y_j$ であることから、
$$
\frac{\partial y_j}{\partial y_k} = \sum_{i} \frac{\partial y_j}{\partial x_i} \frac{\partial x_i}{\partial y_k}
$$
と連鎖律が使えることを利用した。
同様にして、
$$
J_{f^{-1}} J_f = I_m
$$
$J_f$ の逆元(逆行列)を計算すると、
$$
\begin{align}
J_f^{-1} &= J_f^{-1} I_n \
&= J_f^{-1} (J_f J_{f^{-1}}) \
&= (J_f^{-1} J_f) J_{f^{-1}} \
&= I_m J_{f^{-1}} \
&= J_{f^{-1}} \
\end{align}
$$
左辺と右辺を入れ替えて、
$$
\begin{align}
J_{f^{-1}} &= J_f^{-1} \
\end{align}
$$
以上により、Inverse Function theorem の主張を得る。
Jacobians of Invertible function
同次元への可逆関数$f$のヤコビ行列 $J_f$ に対して、以下が成り立つ
$$
\det ( J_f^{-1} ) = \det ( J_f ) ^{-1} \
$$
まず、$f: \mathbb{R}^n \rightarrow \mathbb{R}^n$ なので、$J_f$ は、$n \times n$ 行列
$$
\begin{align}
\det ( J_f^{-1} )
&= \det ( J_f^{-1} ) \cdot 1 \
&= \det J_f^{-1} \left ( \det J_f \right ) \left ( \det J_f \right )^{-1} \
&= \left ( \det J_f^{-1} \det J_f \right ) \det \left ( J_f \right )^{-1} \
&= \det \left ( J_f^{-1} J_f \right ) \det \left ( J_f \right )^{-1} \
&= \det \left ( I_m \right ) \det \left ( J_f \right )^{-1} \
&= \det \left ( J_f \right )^{-1} \
\end{align}
$$
ここで、表記上 $\det J_f = \det ( J_f )$ として適宜、記述した。
右辺の右肩の $-1$ は、逆数の意味である点に注意する。
Chain of Probability Density is Normalizing Flow
$$
\begin{align}
x = z_K &= f_K \circ f_{K-1} \circ \cdots \circ f_1(z_0) \
\log p(x) = \log \pi_K (z_K) &= \log \pi_{K-1}(z_{K-1}) - \log \left | \det \frac{df_K}{dz_{K-1}} \right | \
&= \log \pi_{K-2}(z_{K-2}) - \log \left | \det \frac{df_{K-1}}{dz_{K-2}} \right | - \log \left | \det \frac{df_K}{dz_{K-1}} \right | \
& \vdots \
&= \log \pi_{0}(z_{0}) - \sum_{k=1}^K \log \left | \det \frac{df_{K-k+1}}{dz_{K-k}} \right | \
&= \log \pi_{0}(z_{0}) - \sum_{i=1}^K \log \left | \det \frac{df_i}{dz_{i-1}} \right | & (\because i:=K-k+1) \
\end{align}
$$
- $\{z_i\}_{i=0}^K$ : flow と呼ぶ
- $\{\pi_i\}_{i=0}^K$ : normalizing flow と呼ぶ
- $f_i$ : 以下の性質が要求される
- $f_i$ : 容易に可逆変換にできる
- $\det J_{f_i}$ : 容易(高速)に計算できる
- $f_i$ : NN(DL) などで実現する