モデル構築・適用

この記事の狙い・目的

機械学習を取り入れたAIシステムの構築は、
①データ分析→ ②データセット作成（前処理）→ ③モデルの構築・適用
というプロセスで行っていきます。
その際「前処理」の段階では、データ分析の考察を踏まえて、精度の高いデータセットが作れるよう様々な対応が必要となります。
このブログでは、「前処理（特徴量エンジニアリング）」の工程について初めから通して解説していきます。

プログラムの実行環境

Python3
MacBook pro（端末）
PyCharm（IDE）
Jupyter Notebook（Chrome）
Google スライド（Chrome）

評価比較

from sklearn.model_selection import train_test_split # データ分割
# アルゴリズム
from sklearn.neighbors import KNeighborsRegressor as KNR # K近傍法（回帰）
from sklearn.linear_model import LinearRegression as LR # 線形回帰
from sklearn.linear_model import Ridge, Lasso, ElasticNet # Ridge回帰、Lasso回帰、ElasticNet回帰
from sklearn.svm import SVR # サポートベクトルマシン
from sklearn.ensemble import RandomForestRegressor as RFR # ランダム・フォレスト（回帰）
from xgboost import XGBRFRegressor as XGBRFR # XGBoost
from sklearn.ensemble import GradientBoostingRegressor as GBR # GBDT（勾配ブースティング木）

# 各評価指標
from sklearn.metrics import r2_score as R2
from sklearn.metrics import mean_absolute_error as MAE
from sklearn.metrics import mean_squared_error as MSE

# 評価
def evaluation(model, y_test, y_pred):
    print('='*40)
    print(model.__class__.__name__)
    print('決定係数（R2） = ', R2(y_test, y_pred).round(decimals=3))
    mae = MAE(y_test, y_pred)
    print('平均絶対誤差（MAE） = ', mae.round(decimals=3))
    rmse = np.sqrt(MSE(y_test, y_pred))
    print('平均二乗平方根誤差（RMSE） = ', rmse.round(decimals=3))
    print('RMSE / MAE = ', (rmse / mae).round(decimals=3)) # <, =, > 1.253
    aic = AIC(y_test, y_pred, num_feature=len(boston_df.columns))
    print('AIC = ', aic.round(decimals=3))

    return mae, rmse, aic

# AIC（赤池情報量規準）
def AIC(y_test, y_pred, num_feature):
    num_data = len(y_test) # サンプル数
    mse = MSE(y_test, y_pred) # MSE
    rss = (0.5 * np.sum((y_test - y_pred)**2) / num_data) # 残差平方和
    return (num_data * (np.log(2 * np.pi) * (rss / num_data) + 1)) + 2 * (num_feature + 1)

# データ分割
def data_devide(df, test_size=0.2):
    target = 'MEDV'
    X = df.drop(columns=target, axis=1)
    y = df[target]
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_size, random_state=42)
    return X_train, X_test, y_train, y_test


# モデリング
def modeling(model, df):
    # ホールドアウト法
    X_train, X_test, y_train, y_test = data_devide(df, test_size=0.2)

    # 学習、予測
    model = model
    model.fit(X_train, y_train)
    y_pred = model.predict(X_test).round(decimals=2)

    # 評価
    mae, rmse, aic = evaluation(model, y_test, y_pred)

# モデル
rfr_model = RFR(random_state=42) # ランダムフォレスト
lr_model = LR() # 線形回帰
ridge_model = Ridge() # Ridge
lasso_model = Lasso() # Lasso
gbr_model = GBR(random_state=42) # 勾配ブースティング木
xgbrfr_model = XGBRFR(random_state=42) # XGBoost
knr_model = KNR() # K近傍法（回帰）
svr_model = SVR() # サポートベクトルマシン
models = [rfr_model, lr_model, ridge_model, lasso_model, gbr_model, xgbrfr_model, knr_model, svr_model]

# 調整前のデータで評価
for model in models:
    modeling(model, boston_before)

# 調整後のデータで評価
for model in models:
    modeling(model, boston_df)

• R2
  • 全体的にあてはまりの良さは改善
• RMSE / MAE
  • Ridge、LinearRegressionが一番大きく外していない。ただしR2が高くない
  • RandomForestRegressorは、大きく外している値もある。外れ値をもっと除く。パラメータを変更する。
  • SVRは、一番大きく外している。
• AIC
  • 全体的に改善。複数項目を取り除いたのが効いている。 $$ AIC = n (\log{(2\pi\frac{S_e}{n}+1)} + 2(p + 1)) $$
• $n$ = サンプル数 : len(y_test)
• $S_e$ = 残差平方和
• $p$ = 項目数 : num_feature

学習状況の確認

from sklearn.model_selection import learning_curve # 学習曲線

def plt_learn_curve(model, df):
    # ホールドアウト法
    X_train, X_test, y_train, y_test = data_devide(df, test_size=0.2)

    # データ準備
    train_sizes, train_scores, val_scores = learning_curve(model, X=X_train, y=y_train, train_sizes = np.linspace(0.1, 1.0, 10), cv=5, n_jobs=1)
    train_scores_mean = np.mean(train_scores, axis=1)
    train_scores_std = np.std(train_scores, axis=1)
    val_scores_mean = np.mean(val_scores, axis=1)
    val_scores_std = np.std(val_scores, axis=1)

    # 訓練スコア と 検証スコア をプロット
    print(model.__class__.__name__)
    plt.figure(figsize=[10,4])
    plt.title("学習曲線")
    plt.xlabel("訓練サンプル")
    plt.ylabel("スコア")
    plt.plot(train_sizes, train_scores_mean, 'o-', color="r", label="訓練スコア")
    plt.plot(train_sizes, val_scores_mean, 'o-', color="g", label="検証スコア")

    # 標準偏差の範囲を色付け
    plt.fill_between(train_sizes, train_scores_mean - train_scores_std, train_scores_mean + train_scores_std, color="r", alpha=0.2)
    plt.fill_between(train_sizes, val_scores_mean - val_scores_std, val_scores_mean + val_scores_std, color="g", alpha=0.2)

    # Y軸の範囲指定
    plt.ylim(0.5, 1.0)

    # 凡例の表示位置
    plt.grid()
    plt.legend(loc="best")
    plt.show()

# 調整前のデータで確認
models = [rfr_model, ridge_model, lasso_model, gbr_model, xgbrfr_model]
for model in models:
    plt_learn_curve(model, boston_before)

# 調整後のデータで確認
for model in models:
    plt_learn_curve(model, boston_df)

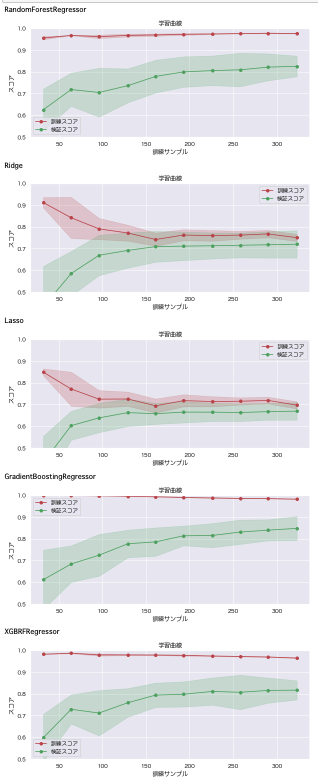
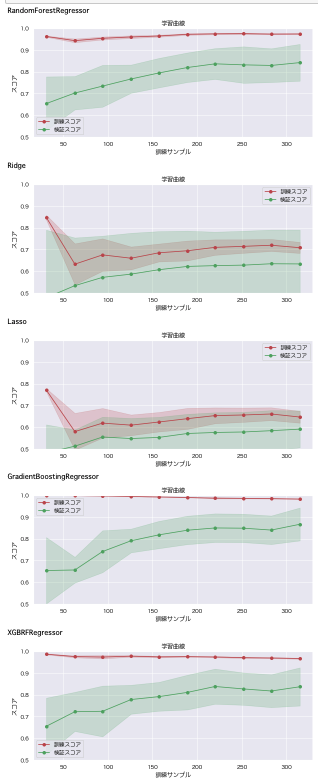
• 調整後の結果
  • 訓練データに適合しているが、検証データに適合しておらず、過学習が起きているものと思われる。
• 調整前後の比較・考察
  • 非線形モデルは調整後の数値が向上している。ただし線形モデルは、調整後の方がスコアが若干下がっている。線形モデル向けに評価が低下した理由を考察し、改善を図ることとする。
  • 調整した意味はありそうだが、過学習を要抑制。「交差検証」で精度の見積もりを行い、「パラメーター・チューニング」で調整を行う必要がありそう。

交差検証

KFold

from sklearn.model_selection import KFold

# Fold数を変化させた評価を比較・考察する。
def fold(model, df, fold):
    # 交差検証
    target = 'MEDV'
    for train_index, val_index in kf.split(df.index):
        X_train = df.drop(columns=target, axis=1).iloc[train_index]
        y_train = df[target].iloc[train_index]
        X_test = df.drop(columns=target, axis=1).iloc[val_index]
        y_test = df[target].iloc[val_index]

        # 学習、予測
        model.fit(X_train, y_train)
        y_pred = model.predict(X_test).round(decimals=2)

        # 評価
        mae, rmse, aic = evaluation(model, y_test, y_pred)

        return rmse_mae, aic

# 実行
models = [rfr_model, ridge_model, xgbrfr_model]
kf = KFold(n_splits=11, shuffle=True) # インスタンス
rmse_maes = []
aics = []
for model in models:
    rmse_mae, aic =  fold(model, boston_df, fold=kf)
    rmse_maes.append(rmse_mae)
    aics.append(aic)

print('='*20)
print('(RMSE / MAE)平均 = ', np.mean(rmse_maes).round(decimals=3))
print('AIC平均 = ', np.mean(aics).round(decimals=3))

fold=11で、（RMSE / MAE）=1.253に一番近づくため、これらの結果を精度目標とする。
AICも100以下を目指して、不要なパラメータを除くようにする。

パラメータ・チューニング

# パラメータ・チューニング
from sklearn.model_selection import RandomizedSearchCV

# 探索用関数
def params_search(df, model, params):
    # データ分割
    X_train, X_test, y_train, y_test = data_devide(df, test_size=0.2)

    # パラメータの探索
    random = RandomizedSearchCV(estimator=model, param_distributions=params)
    random_result = random.fit(X_train, y_train)
    print(random_result)
    print(random.best_params_)
    print(random.best_score_)

ランダム・サーチ

ランダムフォレスト回帰

# ランダムフォレスト（回帰）
params_rfr = {
    'n_estimators' : [i for i in range(10, 100, 10)],
    'max_features' : [i for i in range(1, boston_df.shape[1]-1)],
    'n_jobs' : [i for i in range(1, 10)],
    'min_samples_split' : [i for i in range(10, 100, 10)],
    'max_depth' : [i for i in range(3, 15)]
}
model_rfr = RFR()
params_search(boston_df, model_rfr, params_rfr)

# 結果：{'n_jobs': 1, 'n_estimators': 80, 'min_samples_split': 30, 'max_features': 6, 'max_depth': 11}

Ridge回帰

# Ridge回帰
params_ridge = {
    'alpha' : [i/10 for i  in range(1, 10)],
    'solver' : ['auto','cholesky','sag','saga']
}
model_ridge = Ridge()
params_search(boston_df, model_ridge, params_ridge)

# 結果：{'solver': 'cholesky', 'alpha': 0.9}

勾配ブースティング木

# 勾配ブースティング木
params_gbr = {
    'max_depth' : [i for i in range(5, 15)],
    'subsample' : [i/10 for i  in range(1, 10)],
    'n_estimators' : [i for i in range(900, 1100, 50)],
    'learning_rate' : [i/100 for i  in range(1, 10)]
}
model_gbr = GBR()
params_search(boston_df, model_gbr, params_gbr)

# 結果：{'subsample': 0.6, 'n_estimators': 1050, 'max_depth': 6, 'learning_rate': 0.01}

グリッド・サーチ

# パラメータ・チューニング
from sklearn.model_selection import GridSearchCV

# 探索用関数
def params_search(df, model, params):
    # データ分割
    X_train, X_test, y_train, y_test = data_devide(df, test_size=0.2)

    # パラメータの探索
    grid = GridSearchCV(estimator=model, param_grid=params)
    grid_result = grid.fit(X_train, y_train)
    print(grid_result)
    print(grid.best_params_)
    print(grid.best_score_)

ランダムフォレスト回帰

params_rfr = {
    'n_estimators' : [i for i in range(80, 85)],
    'max_features' : [i for i in range(10, 13)],
    'n_jobs' : [i for i in range(8, 10)],
    'min_samples_split' : [i for i in range(25, 30)],
    'max_depth' : [i for i in range(10, 12)]
}
model_rfr = RFR()
params_search(boston_df, model_rfr, params_rfr)

# 結果：{'n_estimators': 87, 'max_depth': 11, 'max_features': 12, 'min_samples_split': 25, 'n_jobs': 9}

Ridge回帰

params_ridge = {
    'alpha' : [i/10 for i  in range(5, 9)],
    'solver' : ['cholesky','sag','saga']
}
model_ridge = Ridge()
params_search(boston_df, model_ridge, params_ridge)

# 結果：{'alpha': 0.8, 'solver': 'cholesky'}

勾配ブースティング木

params_gbr = {
    'max_depth' : [i for i in range(12, 15)],
    'subsample' : [i/10 for i  in range(4, 8)],
    'n_estimators' : [i for i in range(1030, 1070, 5)],
    'learning_rate' : [i/100 for i  in range(4, 8)]
}
model_gbr = GBR()
params_search(boston_df, model_gbr, params_gbr)

# 結果：{'learning_rate': 0.04, 'max_depth': 14, 'subsample': 0.5}

結果

• ランダムフォレスト回帰
  • {'n_jobs': 8, 'n_estimators': 87, 'min_samples_split': 27, 'max_features': 10, 'max_depth': 8}
• Ridge回帰
  • {'solver': 'cholesky', 'alpha': 0.8}
• 勾配ブースティング木
  • {'subsample': 0.5, 'n_estimators': 1030, 'max_depth': 12, 'learning_rate': 0.05}

再評価

# モデリング
def modeling(model, df):
    # データ分割
    X = df.drop('MEDV',axis=1)
    y = df['MEDV']
    X_train,X_test,y_train,y_test = train_test_split(X, y, test_size=0.2, random_state=42)

    # 学習、予測
    model = model
    model.fit(X_train, y_train)
    y_pred = model.predict(X_test).round(decimals=2)

    # 評価
    mae, rmse, aic = evaluation(model, y_test, y_pred)

    return model

# ランダムフォレスト
rfr_model = RFR(
    n_estimators=87,
    max_features=10,
    n_jobs=8,
    min_samples_split=27,
    max_depth=87
)
# Ridge
ridge_model = Ridge(
    alpha=0.8,
    solver='cholesky'
)
# 勾配ブースティング木
gbr_model = GBR(
    max_depth=12,
    subsample=0.5,
    n_estimators=1030,
    learning_rate=0.05
)
models = [rfr_model, ridge_model, gbr_model]

# 評価
mdls = {}
for model in models:
    mdl = modeling(model, boston_before)
    mdls[model.__class__.__name__] = mdl

# 学習曲線
for name, model in mdls.items():
    plt_learn_curve(model, boston_df)

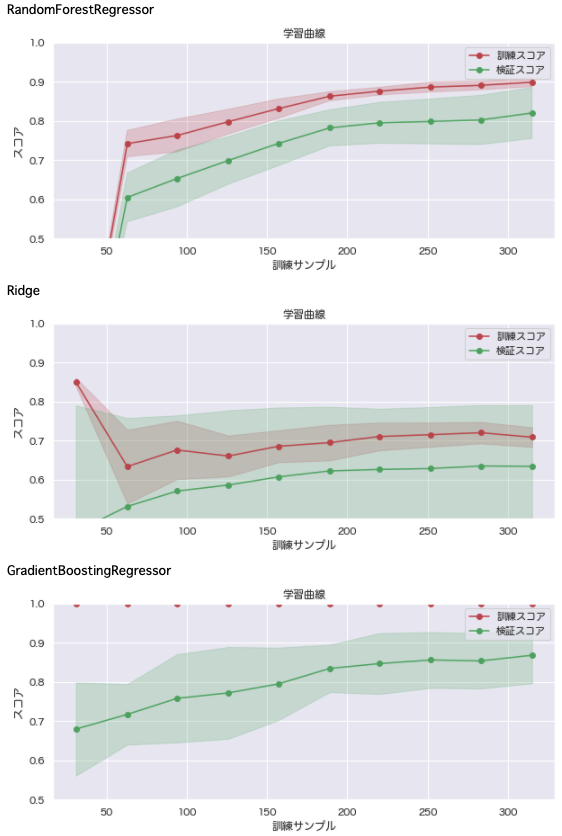
Ridge回帰が精度低め。（Ridgeの学習時に）データセットをRidge向けに変換する。
XGBoostは過学習をおこしているため、過学習対策を行う。

学習データの調整

from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler

# ランダムフォレスト回帰
rfr_model = RFR(
    n_estimators=87,
    n_jobs=8,
    min_samples_split=27,
    max_depth=87
)
# Ridge回帰
ridge_model = make_pipeline(
    StandardScaler(),# 標準化
    Ridge(alpha=0.8, solver='cholesky')
)
# 勾配ブースティング木
gbr_model = GBR(
    max_depth=12,
    subsample=0.5,
    n_estimators=1030,
    learning_rate=0.05,
    validation_fraction=0.1, # 過学習対策
    n_iter_no_change=3, # 過学習対策
    tol=0.001 # 過学習対策
)

models = [rfr_model, ridge_model, gbr_model]

# 評価
mdls = {}
for model in models:
    mdl = modeling(model, boston_before)
    mdls[model.__class__.__name__] = mdl

# 学習曲線
for name, model in mdls.items():
    plt_learn_curve(model, boston_df)

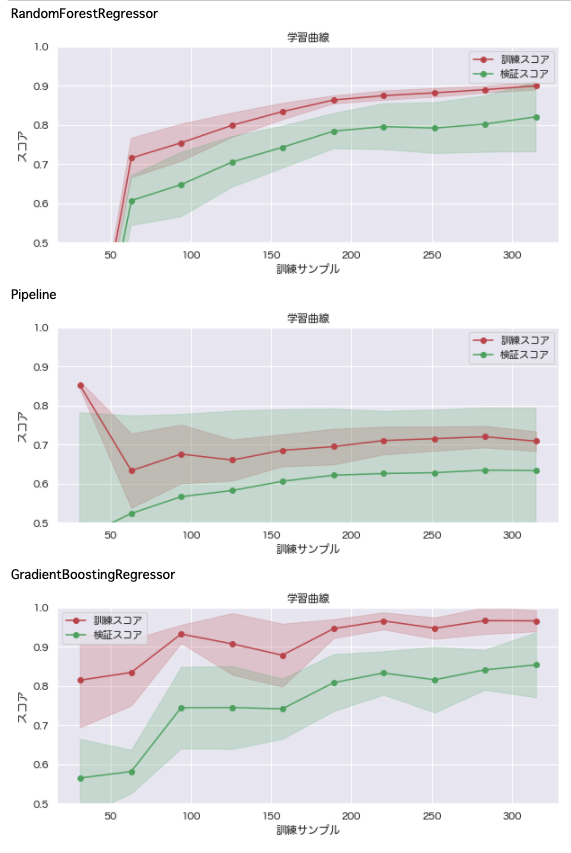
訓練スコアと検証スコアの差が全体的に縮まり、過学習が改善されている。
ただい検証スコア自体にあまり大きな変化はない。この後のアンサンブル学習の評価でどこまで良くなるか確認する。

アンサンブル

# スタッキング
# ホールドアウト法
X_train, X_val, y_train, y_val = data_devide(boston_df, test_size=0.3)

X_train = X_train.reset_index(drop=True)
X_val = X_val.reset_index(drop=True)
y_train2 = y_train.reset_index(drop=True)
y_val = y_val.reset_index(drop=True)

# モデル
models = [rfr_model, ridge_model, gbr_model]

preds = []
for model in models:
    cv = KFold(n_splits=11, random_state=42, shuffle=True)

    pred_model = np.zeros(len(y_train))
    for trn_index, val_index in cv.split(X_train):
        X_trn, X_val = X_train.iloc[trn_index], X_train.iloc[val_index]
        y_trn, y_val = y_train.iloc[trn_index], y_train.iloc[val_index]

        model.fit(X_trn, y_trn)

        pred_model[val_index] = model.predict(X_val)

    preds.append(pred_model)

# 2層目の学習データとして用いる為、学習データの予測値を取得
kf_train = pd.DataFrame({"RFR_予測":preds[0], "RIDGE_予測":preds[1], "DGBR_予測":preds[2]})
# display(kf_train)

# テストデータの予測値を取得
pred_tests = []
for model in models:
    model.fit(X_train, y_train)
    pred_test = model.predict(X_val)
    pred_tests.append(pred_test)

# 2層目の予測データとして用いるため、テストデータの予測値を取得
kf_tests = pd.DataFrame({"RFR_予測":pred_tests[0], "RIDGE_予測":pred_tests[1], "DGBR_予測":pred_tests[2]})
# display(kf_tests)

# 2層目は「ランダムフォレスト回帰」で予測
model2 = rfr_model
model2.fit(kf_train, y_train)
pred_stack = model2.predict(kf_tests)

# １層目の予測値
kf_train.head()

kf_tests.head()

# スタッキングの評価
mae, rmse, aic = evaluation(model2, y_val, pred_stack)

最高スコア。交差検証で当初見積もっていた目標値よりも良い結果を出せました。

まとめ

モデルの構築・適用を行ってみて、まだまだデータ分析、前処理の工程の進め方が甘いと認識しました。特に線形モデルの精度が上がらず改善が必要そうです。過学習の対策も行っていますが、まだ少し訓練スコアと検証スコアに差があり、パラメータの調整でもう少し改善できるかもしれません。Kaggleの他の方の実装なども参考にしながら改善点を模索していきたいと思います。

最後に

他の記事はこちらでまとめています。是非ご参照ください。

解析結果

実装結果：GitHub/boston_regression_modeling.ipynb
データセット：Boston House Prices-Advanced Regression Techniques

参考資料