Kerasで多変量LSTM

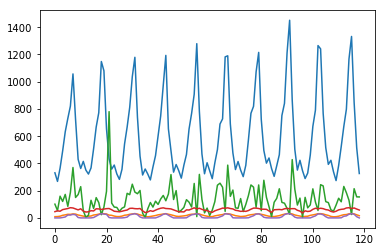
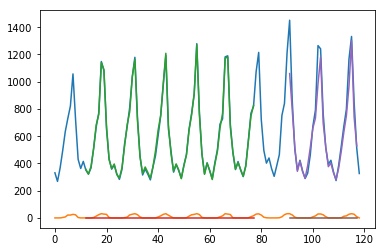
単変量の時系列はkerasでもよく見るのですが、株価や売上などを予測する時などには複数の要因が関わってきますので、今回は複数の時系列データを使って予測してみました。

ソースの紹介

コード

「MACHINE LEARNING MASTERY」で紹介されているコードを基本に、多変量対応にしました。
Time Series Prediction with LSTM Recurrent Neural Networks in Python with Keras

jupyterで見れるコードの全貌はこちら
https://github.com/tizuo/keras/blob/master/LSTM%20with%20multi%20variables.ipynb

データ

サンプルデータは以下から拝借しました。一番左のice_salesを予測します。
アイスクリームの売れ方

ice_sales	year	month	avg_temp	total_rain	humidity	num_day_over25deg
331	2003	1	9.3	101	46	0
268	2003	2	9.9	53.5	52	0
365	2003	3	12.7	159.5	49	0
492	2003	4	19.2	121	61	3
632	2003	5	22.4	172.5	65	7
730	2003	6	26.6	85	69	21
821	2003	7	26	187.5	75	21

データの標準化

データを標準化します。LSTMはセンシティブなので扱う数値を標準化されなければならないと説明されていました。

scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(dataset)

テストデータを分ける

今回は後半1/3のデータを予測させますので、学習用と分けます。

train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]

データの整形

3ヶ月前までの値を使って次の月の値を学習させるので、以下のような形で整形します。
これを使う変数分作成し、1時点分のデータにそれぞれ格納します。

Y	3ヶ月前	2ヶ月前	1ヶ月前
1月の値	10月の値	11月の値	12月の値
2月の値	11月の値	12月の値	1月の値
3月の値	12月の値	1月の値	2月の値

今回は年間で1セットとみなし、ルックバックは12でデータを作ります。

def create_dataset(dataset, look_back=1):
    dataX, dataY = [], []
    for i in range(len(dataset)-look_back-1):
        xset = []
        for j in range(dataset.shape[1]):
            a = dataset[i:(i+look_back), j]
            xset.append(a)
        dataY.append(dataset[i + look_back, 0])      
        dataX.append(xset)
    return numpy.array(dataX), numpy.array(dataY)

look_back = 12
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)

このデータをkerasのLSTMで受け付けられている形式に変換します。
[行数]＞[変数数]＞[カラム数(ルックバック数)]

trainX = numpy.reshape(trainX, (trainX.shape[0], trainX.shape[1], trainX.shape[2]))
testX = numpy.reshape(testX, (testX.shape[0], testX.shape[1], testX.shape[2]))

モデル作成

input_shapeには、変数数とルックバック数が入ります。出力数は特に考えず、サンプル通り4にしています。

model = Sequential()
model.add(LSTM(4, input_shape=(testX.shape[1], look_back)))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(trainX, trainY, epochs=1000, batch_size=1, verbose=2)

検証

予測は通常と同じです。

trainPredict = model.predict(trainX)
testPredict = model.predict(testX)

この後、Yを標準化前の数字に戻します。scalerが元のデータセットと同じ形でないと受け付けられないため、存在していたカラムの数だけ値を0で埋めています。
もっとスマートな方法があれば誰か教えてください。

pad_col = numpy.zeros(dataset.shape[1]-1)
def pad_array(val):
    return numpy.array([numpy.insert(pad_col, 0, x) for x in val])

trainPredict = scaler.inverse_transform(pad_array(trainPredict))
trainY = scaler.inverse_transform(pad_array(trainY))
testPredict = scaler.inverse_transform(pad_array(testPredict))
testY = scaler.inverse_transform(pad_array(testY))

ようやく標準偏差を出します。

trainScore = math.sqrt(mean_squared_error(trainY[:,0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = math.sqrt(mean_squared_error(testY[:,0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))

変数の数を変えていったところ、以下のようになりました。
当然ですが、投げる変数は選ばないといけませんね。

	アイスクリームの売上だけで学習したモデル	アイスと25度以上日数	全部
Train Score	30.20 RMSE	15.19 RMSE	8.44 RMSE
Test Score	111.97 RMSE	108.09 RMSE	112.90 RMSE