楽するライフゲーム / Python

ライフゲームを考案したジョン・ホートン・コンウェイは2020年4月11日(土曜日)、新型コロナウイルスが原因で亡くなった。82歳であった。

概要

極力外部モジュールを使ってライフゲームを実装してみる。配列は、上辺と下辺とがつながっていて、かつ左辺と右辺とがつながっているものとする。

完成したコード

life.py

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import convolve2d as convol
from matplotlib.animation import FuncAnimation as anim
class LifeGame:
    def __init__(self, mat, figsize=None, interval=1):
        self.mat = np.asarray(mat, dtype=np.uint8)
        self.RULE = np.array([[0,0,0,1,0,0,0,0,0],
                              [0,0,1,1,0,0,0,0,0]], dtype=np.uint8)
        self.WEIGHT = np.array([[1,1,1],
                                [1,0,1],
                                [1,1,1]], dtype=np.uint8)
        _ = anim(plt.figure(figsize=figsize), self.__update, interval=interval)
        plt.show()
    def __update(self, _):
        plt.clf()
        plt.imshow(self.mat, cmap="binary")
        self.mat = self.RULE[self.mat, convol(self.mat, self.WEIGHT, "same", "wrap")]

if __name__ == "__main__":
    mat = np.eye(212, dtype=np.uint8) # 大きなＸ字を初代配列としてライフゲームを実行してみる。
    LifeGame(mat | mat[::-1]) # 構文: LifeGame(値が1または0のみの2次元配列)

実行結果:

解説

(1) scipy.signal.convolve2d()でムーア近傍の和を求める

これがライフゲームの一番の肝である。

moore.py

import numpy as np
from scipy.signal import convolve2d

# この配列glider0の全セルのムーア近傍の和を求めてみる。
glider0 = np.array([[0,0,0,0,0,0,0],
                    [0,0,1,0,0,0,0],
                    [0,0,0,1,0,0,0],
                    [0,1,1,1,0,0,0],
                    [0,0,0,0,0,0,0]], dtype=np.uint8)

# 畳み込みの重みづけを定義しておく。
weight = np.array([[1,1,1],
                   [1,0,1],
                   [1,1,1]], dtype=np.uint8)

# これが配列glider0の全セルのムーア近傍の和である。boundary="wrap"オプションを指定すると配列の上下左右がつながっていることになる。
moore = convolve2d(glider0, weight, boundary="wrap", mode="same")
    
print(glider0)
print(moore)

実行結果(上が現世代配列、下がその全セルのムーア近傍の和):

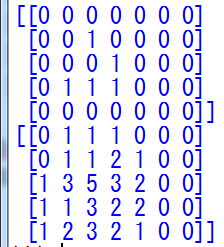
(2) 1世代進める

ルール配列を定義しておいて現世代配列とムーア近傍の和とをインデックスにしてルール配列を検索することにする。
たとえば、現世代配列のセルが0 (死)、そのセルのムーア近傍の和が5である場合は、ルール配列のインデックス[0, 5]を検索して次世代の生死を0 (死)に決定する。

ルール配列:

ムーア近傍の和	0	1	2	3	4	5	6	7	8
現在死セル(0)の次の状態	0	0	0	1	0	0	0	0	0
現在生セル(1)の次の状態	0	0	1	1	0	0	0	0	0

update.py

import numpy as np
from scipy.signal import convolve2d

# この配列を1世代進めてみる。
glider0 = np.array([[0,0,0,0,0,0,0],
                    [0,0,1,0,0,0,0],
                    [0,0,0,1,0,0,0],
                    [0,1,1,1,0,0,0],
                    [0,0,0,0,0,0,0]], dtype="uint8")

# ルール配列を定義しておく。
Rules  = np.array([[0,0,0,1,0,0,0,0,0],
                   [0,0,1,1,0,0,0,0,0]], dtype="uint8")

# 畳み込みの重みづけを定義しておく。
Weight = np.array([[1,1,1],
                   [1,0,1],
                   [1,1,1]], dtype="uint8")

# これがムーア近傍の和である。
moore = convolve2d(glider0, Weight, mode="same", boundary="wrap")

# これが次世代配列である。
glider1 = Rules[glider0, moore]

print(glider0)
print(glider1)

実行結果(上が現世代配列、下が次世代配列):

(3) 2次元の生死配列を描画する

ここではmatplotlib.pyplot.imshow()を使う。

showImg.py

import numpy as np
import matplotlib.pyplot as plt

# この生死配列を表示してみる。
glider = np.array([[0,0,0,0,0,0,0],
                   [0,0,1,0,0,0,0],
                   [0,0,0,1,0,0,0],
                   [0,1,1,1,0,0,0],
                   [0,0,0,0,0,0,0]], dtype="uint8")

plt.imshow(glider, cmap="binary")
plt.grid()
plt.show()

実行結果:

(4) 2次元配列の変化をアニメ化する

ループは使わずにmatplotlib.animation.FuncAnimation()を使ってみる。例として、一定時間ごとに乱数配列を更新してそれを動画として観測する。下の例はライフゲームではない。

anim.py

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

# この関数を一定時間ごとに繰り返し実行することにする。
# 引数iはFuncAnimation()から渡されるフレーム番号(を受けるための変数)であるがここでは使っていない。
def update(i):
    plt.clf()
    mat = np.random.randint(0, 2, [20, 30]) # 20行30列の2値乱数配列を生成して、
    plt.imshow(mat, cmap="binary") # 図として表示する。

# 表示領域を設定しておく。
fig = plt.figure()

# 「どの表示領域(fig)」で「どの関数(update)」を「何ミリ秒おき(interval=)」に実行するのかを指定する。
_ = FuncAnimation(fig, update, interval=500)
plt.show()

実行結果:

課題

描画の更新が遅い。表示領域を拡げたときは特に遅い。

参考

• https://qiita.com/krrka/items/e5c0720ac6382e61dc60
• 三井和男, 2010年,『Excelコンピュータシミュレーション 数学モデルを作って楽しく学ぼう』, pp.144-166, 森北出版
• https://qiita.com/cyq04000/items/0d9a70c4dbc0aa738902

関連

• http://ti-nspire.hatenablog.com/archive/category/%E3%83%A9%E3%82%A4%E3%83%95%E3%82%B2%E3%83%BC%E3%83%A0